基于實際工況的零件公差規范設計方法*

孫永厚，肖振泉，黃美發，張　驥

(1.桂林電子科技大學 機電工程學院，廣西 桂林　541004；2.廣西制造系統與先進制造技術重點實驗室，廣西 桂林　541004)

?

基于實際工況的零件公差規范設計方法*

孫永厚1,2，肖振泉1，黃美發1,2，張驥1

(1.桂林電子科技大學 機電工程學院，廣西 桂林541004；2.廣西制造系統與先進制造技術重點實驗室，廣西 桂林541004)

摘要：傳統的零件公差規范設計一般只考慮功能要求和加工工藝，忽略實際工況的影響。針對以上不足，提出了一種基于實際工況的零件公差規范設計方法。首先依據小位移旋量(SDT)理論，建立零件公差數學模型；然后根據蒙特卡羅法求得實際要素的極限位置，生成模擬點并擬合得到規范表面模型，再轉化為實體模型；最后通過有限元仿真，獲得實際工況下的實體模型，對其進行規范操作，確定幾何要素的最大偏差。通過實例分析，驗證了該方法的可行性。

關鍵詞：實際工況；蒙特卡羅；規范表面模型

0引言

零件公差規范設計是指設計工程師基于幾何產品的功能要求，利用表面模型對實際工件表面進行模擬，對限定要素進行分離、提取、濾波、擬合等操作，確定在滿足功能要求前提下幾何要素的最大偏差，用來指導公差設計的過程。近年來，不少專家學者對零件公差規范設計進行了研究[1-3]，但大多數研究只考慮零件的功能要求和加工工藝，忽略了實際工況的影響；而零件在實際工況下會承受工作載荷，由此造成的變形會影響到零件功能要求。因此，設計者在公差規范設計階段需要考慮實際工況的影響，以便合理地設計公差。針對上述問題，在前人研究基礎上提出一種基于實際工況的零件公差規范設計方法，綜合考慮零件功能、加工工藝和實際工況的影響，通過一個實例闡述該方法步驟，驗證該方法的可行性。

1傳統零件公差規范設計

傳統零件公差規范設計僅考慮零件功能要求和加工工藝的影響，忽略零件在實際工況下所受載荷，其主要步驟：

步驟1：建立公差數學模型。目前，大都采用小位移旋量(SDT)理論進行公差的統一表達。SDT理論的基本思想是將特征的幾何缺陷看作是三維歐式空間中點集運動的結果，并應用微小矢量來表示點的空間運動，最早由 Bourdet 在1996年引入到公差領域[4]。SDT可以寫成：

(1)

式中：θx、θy、θz表示理想要素繞X，Y，Z軸的轉動；dx、dy、dz表示理想要素繞X，Y，Z軸的平動。根據SDT理論，首先求出理想要素的變動方程(以SDT分量為控制變量)；然后根據公差約束條件，確定SDT分量的變動范圍和約束條件，從而建立公差數學模型(此處的變動方程和SDT分量皆是關于公差域邊界旋量參數)。

步驟2：確定公差帶邊界的位置。

步驟3：分析零件的功能要求對規范表面模型的影響。

步驟4：分析零件加工工藝對規范表面模型的影響，實際零件的誤差主要與加工工藝有關，因此需要建立加工誤差的數學模型。

步驟5：生成模擬實際工件的模擬點。

步驟6：對生成的模擬點進行插值或擬合操作，得到規范表面模型。

2基于實際工況的零件公差規范設計

實際工況下的零件公差規范設計方法步驟：①建立公差數學模型。②確定公差帶邊界的位置。③運用蒙特卡羅法求出實際要素在公差域中的極限位置。④考慮功能要求和加工工藝的影響，建立規范表面模型。⑤根據規范表面模型生成相應的實體模型。⑥分析實際工況載荷對規范表面模型的影響。下面僅介紹步驟中的③和⑥兩步，其他步驟與傳統零件公差規范設計方法類似，不再介紹。

2.1蒙特卡羅法求解實際要素的極限位置

公差數學模型只確定了公差域邊界的變動范圍和約束條件，并沒有確定出實際要素在公差域的位置。本文需要求出實際要素在公差域中的極限位置(因為若實際要素處于極限位置情況下能符合功能要求，則其他位置也能符合功能要求)；而求極限位置，關鍵是求實際要素旋量參數的極值。

蒙特卡羅法是一種直觀高效的數值模擬方法，以數理統計和概率論為基礎，在解決可靠性小樣本數據和非線性復雜狀態函數問題方面有比較好的效果[5]。因多種因素綜合作用的影響，實際要素在公差域內具有隨機性，因此實際要素的旋量參數是隨機變量[6]，能用蒙特卡羅法求其極值。以圓柱度公差(圓柱度公差域邊界旋量參數僅需考慮θx1，θy1，dx1，dy1；同樣地，實際要素旋量參數僅需考慮θx2，θy2，dx2，dy2[7])為例敘述具體求解步驟：

步驟1：確定公差域邊界旋量參數θx1、θy1、dx1、dy1的理想概率分布模型，一般假定為正態分布。

步驟3：對邊界旋量參數進行抽樣，獲取實際要素旋量參數(θx2，θy2,dx2,dy2)的樣本，抽樣如圖1所示。圖中k為抽樣次數，K為預定實際要素旋量參數樣本數。至此，可得到K組實際要素旋量參數本。

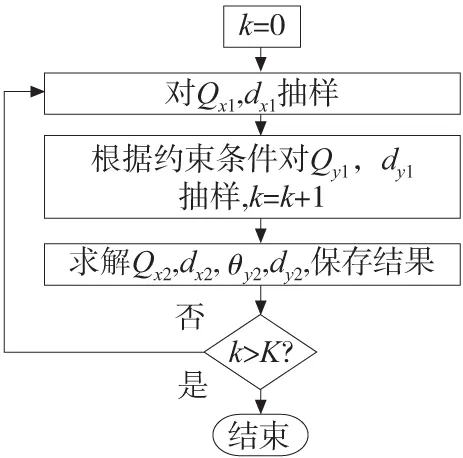
圖1　抽樣流程圖

步驟4：進行實際要素旋量參數實際分布函數的假設檢驗，本文采用卡方擬合檢驗法。

步驟5：采用極大似然法估計實際分布函數的參數。

步驟6：求解實際要素旋量參數的極值根據參數實際分布函數類型與均方差，可求得參數的實際變動區間帶寬：

(2)

則實際要素旋量參數的極值：

(3)

以上兩式中：x=θx2、θy2、dx2、dy2，K為相對分布系數，e為相對不對稱系數[8]。

2.2分析實際工況載荷對規范表面模型的影響

求得實際要素旋量參數的極值后，根據加工工藝和功能要求生成模擬點，對模擬點進行擬合生成規范表面模型；下面分析實際工況對規范表面模型的影響。

(1)有限元分析。首先根據規范表面模型生成三維實體模型；然后對三維實體模型進行實際工況載荷下的有限元分析，得到實際工況載荷下的變形體。

(2)獲取帶有變形信息的點。

①提取實體模型變形前的點集，這需要用到新一代GPS標準中分離與提取兩種要素操作。在對三維實體模型進行有限元分析時，會在模型表面生成足夠多個有限元節點，且模型具有近乎規則的幾何特征，因此分離與提取等價于提取有限元節點；并且若有限元分析無誤，節點中不會存在奇點，一般不需要進行濾波操作，這將大大減少工作量。

②獲取各個節點在X,Y,Z坐標方向上的變形量，并提取的有限元節點坐標進行疊加處理，得到帶有變形信息的一組數據點。

③對帶有變形信息的數據點進行誤差評價，獲得實際工況載荷下實體模型最大幾何偏差。

3算例分析

如圖2所示，尾座頂尖由3個零件組成，其中對零件3的圓柱面有圓柱度公差要求；圓柱度公差值TF為0.003mm，直徑d為100mm，上偏差TSH為0，下偏差TSL為-0.004mm，尺寸公差TS=TSH-TSL=0.004mm，長度L為200mm[9]。下面分別介紹基于實際工況的零件公差規范設計方法和傳統零件公差規范設計方法。

圖2　機床尾座頂尖示意圖

3.1基于實際工況的零件公差規范設計方法

3.1.1建立圓柱度公差數學模型

根據SDT理論，圓柱度公差數學模型[7]如下所示：

變動：

(4)

(5)

(6)

(7)

約束：

(8)

(9)

代入數據，可得：

變動：

(10)

約束：

(11)

3.1.2蒙特卡羅法求解實際要素極限位置

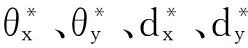
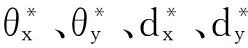
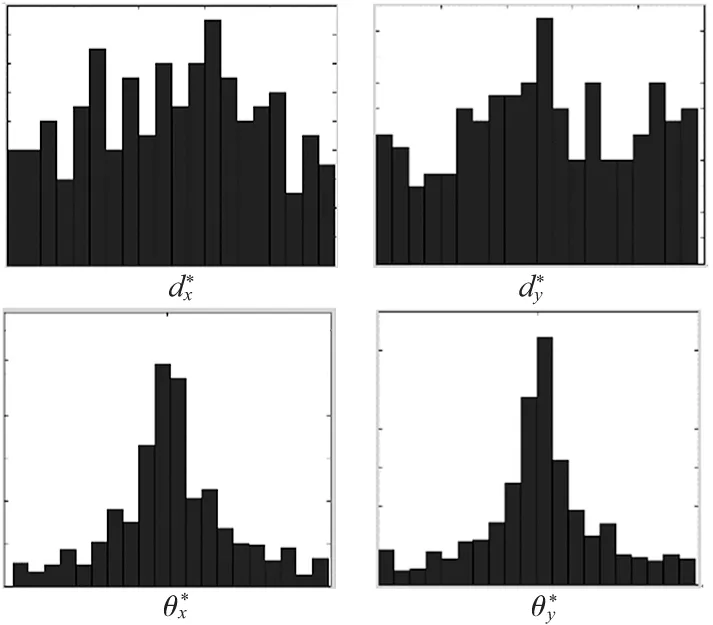
圖3　實際要素旋量參數頻數直方圖

(3)求實際要素旋量參數的極值。

(12)

(13)

(14)

3.1.3生成規范表面模型

(1)零件的功能要求。對于本例中的頂尖，滿足其公差值就能滿足功能要求。

(2)加工工藝的影響。圓柱形零件經加工后會形成四種類型的圓柱面：錐形、凹形、凸形、香蕉形。對于頂尖插入端，經加工后會產生凸形圓柱面，加工誤差：

Δt=A-B·(3·z2-1)

(15)

A，B為常數(根據具體公差值選取)，z為零件軸線上的坐標值[2]。本例頂尖插入端的圓柱度公差為0.003mm，可取A=-0.0000001，B=0.0000001。

(3)在圓柱度公差域內生成模擬點。根據加工誤差生成模擬點，如4圖所示。

(4)生成規范表面模型。根據模擬點生成頂尖插入端的規范表面模型，如5圖所示。

3.1.4分析實際工況對規范表面模型的影響

(1)有限元分析。建立頂尖實體模型時，插入端按上述規范表面模型生成實體模型，其余部分按理想情況建模；對頂尖實體模型進行實際工況載荷的有限元分析，得到其變形情況，如圖6所示。

(2)分析實際工況對規范表面模型的影響。由于本例僅分析頂尖插入端圓柱面的圓柱度誤差，因此只需提取插入端圓柱面的節點以及節點位移信息，將兩者相加便可得到變形后的節點坐標。對變形點數據進行規范操作，評估結果：0.0032mm，并以此值修正初始公差值。

圖4　模擬點

圖5　規范表面模型

圖6　頂尖變形云圖

圖7　規范表面模型

3.2傳統公差規范設計方法

具體步驟參照第2節。首先根據公差數學模型，生成符合變動不等式和約束條件的邊界旋量參數值：θx=-0.0000026564，θy=-0.0000036133，dx=-0.0036，dy=-0.0022。然后根據零件功能和加工工藝，生成體現誤差的模擬點；最后擬合模擬點生成規范表面模型，如圖7所示；并對其進行操作，評估結果：0.0025mm。

3.3分析結果比較

根據兩種零件公差規范設計方法，分別進行10次公差規范設計，編寫相應程序得到相應圓柱度誤差值，如圖8所示，圖中橫坐標表示規范設計的次數，縱坐標表示相應次數的圓柱度誤差值；對所得結果進行分析，如表1所示。

由分析結果可知，實際工況載荷使頂尖圓柱度誤 差期望值增大了28.7%，方差(波動)增大了35.4%，并且期望值超出初始設定公差值；可見，頂尖的實際工況載荷對規范設計結果之一─規范特征值產生很大的影響，也間接影響了測量、認證相關規范的制定。因此，對于精密機械系統而言，實際工況載荷不可忽視，在公差規范設計時，將其作為重要因素考慮，可真實地預測零件在實際工作環境下的變形，以便制定出合理的GPS規范。

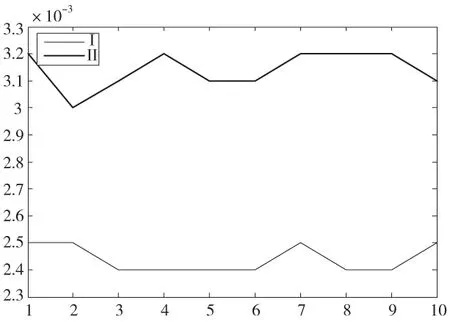
圖8　兩種方法結果

規范設計方法類型期望/mm方差/mm傳統公差0.002440.00004899實際工況0.003140.000066332

4結束語

以SDT理論和蒙特卡羅法為基礎，提出了一種基于實際工況的零件公差規范設計方法；以某車床尾座頂尖為例，分別應用本文提出方法和傳統零件公差規范設計方法，對比了二者的規范設計結果，驗證了本文提出方法的可行性與合理性，使公差的規范設計符合工程實際情況。

[參考文獻]

[1] 李向前.基于新一代GPS的形狀公差規范設計方法研究[D].桂林:桂林電子科技大學,2010.

[2] 周鑫.基于GPS的典型幾何特征數字化建模及規范設計研究[D].鄭州:鄭州大學,2012.

[3] 彭娟.基本恒定類表面模型及操作算子的研究[D].桂林:桂林電子科技大學,2010.

[4] Bourdet P, Clement A. A study of optimal criteria identification based on the small displacement screw mode [J]. Annals of the CIRP, 1988, 37: 503-50.

[5] 庹奎，胡啟國，謝國賓. 基于ANSYS的連桿結構強度混合可靠性分析[J]. 組合機床與自動化加工技術，2014(6)：113-114.

[6] ZHONG Xin, YANG Ruqing, ZHOU Bing. Accuracy analysis of assembly success rate with Monte Carlo simulation [J]. Journal of Donghua University, 2003, 20(3): 128-131.

[7] 張嬌娜.基于GPS標準體系的形狀公差建模及其誤差評價技術[D].杭州:浙江大學,2007.

[8] 王先逵. 機械制造工藝學[M].北京:機械工業出版社,2013.

[10] 王兆證.計算機輔助尺寸公差設計的研究[D]. 南京:南京農業大學,2002.

(編輯趙蓉)

The Specification Design of Tolerance Based on Working Load

SUN Yong-hou1,2, XIAO Zhen-quan1, HUANG Mei-fa1,2, ZHANG Ji1

(1.School of Mechanical and Electrical Engineering,Guilin University of Electronic and Technology, Guilin Guangxi 541004,China；2.GuangXi Key Laboratory of Manufacturing System &Advanced Manufacturing Technology, Guilin Guangxin 541004,China)

Abstract：Generally, the traditional specification design of tolerance of part only considers functional requirements and processing of part, ignoring the effect of the actual working situation. Faced with the lack above, a method of specification design of tolerance of part based on the actual working situation is proposed. Firstly, a tolerance mathematical model is built according to the theory of Small Displacement Torsor (SDT). Then, extreme position of actual feature is got by Monte Carlo method. Simulation points are produced and Specification surface model is obtained by fitting, which is next translated into solid model. Finally, solid model under the actual working situation is gained by finite element stimulation, whose specification operation is proceed to determine the maximum deviation of geometrical feature. The feasibility of proposed method is verified by an analysis of example.

Key words：the actual working situation; monte carlo; specification surface model

文章編號：1001-2265(2016)05-0009-04

DOI:10.13462/j.cnki.mmtamt.2016.05.003

收稿日期：2015-06-03；修回日期：2015-07-16

*基金項目：國家自然科學基金(51365009)；廣西制造系統與先進制造技術重點實驗室主任課題(13-051-09-009Z)資助項目；桂林電子科技大學研究生教育創新計劃資助項目(GDYCSZ201445)

作者簡介：孫永厚(1967—)，男，山東沂水人，桂林電子科技大學教授，工學碩士，研究方向為現代設計與制造技術、新一代GPS標準體系理論以及故障診斷專家系統，(E-mail)zyx881123@163.com。

中圖分類號：TH161+.21;TG506

文獻標識碼：A