GA改進(jìn)BP神經(jīng)網(wǎng)絡(luò)在抗滑樁孔爆破開挖中的應(yīng)用

岳 衡， 韓翔宇， 張繼春， 潘 強， 李鵬川， 陽 陶

(西南交通大學(xué) 土木工程學(xué)院, 成都 610036)

?

GA改進(jìn)BP神經(jīng)網(wǎng)絡(luò)在抗滑樁孔爆破開挖中的應(yīng)用

岳 衡， 韓翔宇， 張繼春， 潘 強， 李鵬川， 陽 陶

(西南交通大學(xué) 土木工程學(xué)院, 成都 610036)

摘要：目前樁孔開挖主要依靠工程類比進(jìn)行，不同設(shè)計者設(shè)計的爆破參數(shù)往往因掌握的爆破理論和經(jīng)驗的不同而有所差異，爆破質(zhì)量參差不齊。為此，提出基于遺傳算法GA改進(jìn)BP神經(jīng)網(wǎng)絡(luò)(GA-BP)建立爆破參數(shù)優(yōu)化設(shè)計模型，該法不僅可以利用已有爆破經(jīng)驗數(shù)據(jù)和工程地質(zhì)條件，同時，使用遺傳算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)閾值和權(quán)值可以彌補BP神經(jīng)網(wǎng)絡(luò)不穩(wěn)定的缺陷，以達(dá)到獲得更優(yōu)爆破參數(shù)的目的。實踐表明，基于遺傳算法改進(jìn)BP神經(jīng)網(wǎng)絡(luò)相比一般BP神經(jīng)網(wǎng)絡(luò)預(yù)測相對誤差較小，同時GA-BP神經(jīng)網(wǎng)絡(luò)得到的優(yōu)化爆破參數(shù)進(jìn)行現(xiàn)場試驗，取得了良好的爆破效果。因此，GA-BP神經(jīng)網(wǎng)絡(luò)模型應(yīng)用于抗滑樁孔開挖爆破參數(shù)設(shè)計是可行的，可用于指導(dǎo)爆破施工。

關(guān)鍵詞：爆破參數(shù)優(yōu)化； BP神經(jīng)網(wǎng)絡(luò)； 遺傳算法； 現(xiàn)場試驗； 樁孔開挖； 爆破開挖

1引 言

由于爆破施工具有工效高、速度快、費用低的特點，在各種類型的巖基樁孔開挖中得到了廣泛應(yīng)用〔1-3〕。目前，樁孔開挖爆破設(shè)計主要是按照工程類比法進(jìn)行，其設(shè)計質(zhì)量所決定的爆破效果與設(shè)計者掌握的爆破設(shè)計理論及其工程經(jīng)驗密切相關(guān)，而且在利用已有工程經(jīng)驗方面，不同的設(shè)計者的爆破方案往往存在較大差異，爆破質(zhì)量因人而異〔4-6〕。究其原因，就是缺少能夠定量利用已有工程經(jīng)驗(主要是爆破參數(shù))的合理方法，特別是很難在爆破設(shè)計中定量引入樁孔基巖的物理力學(xué)參數(shù)。此外，在通過現(xiàn)場爆破試驗進(jìn)行所設(shè)計樁孔爆破參數(shù)的優(yōu)化時，往往不能做到爆破參數(shù)對爆破效果影響作用的定量分析，因而爆破參數(shù)的優(yōu)化常常是人為因素偏多，這對于缺乏爆破工程實踐經(jīng)驗或爆破工程經(jīng)驗不多的設(shè)計者而言，就更難正確合理地選取爆破參數(shù)。為此，有必要提出可定量利用已有爆破經(jīng)驗數(shù)據(jù)和工程地質(zhì)條件的設(shè)計計算方法。

不少設(shè)計者借鑒BP神經(jīng)網(wǎng)絡(luò)對露天礦山和巖體等進(jìn)行爆破參數(shù)設(shè)計〔7-8〕。該方法充分利用已有工程經(jīng)驗對爆破參數(shù)的設(shè)計，并考慮了基巖物理力學(xué)參數(shù)，但在建立BP網(wǎng)絡(luò)模型時，往往由于初始網(wǎng)絡(luò)連接權(quán)值和閾值產(chǎn)生的隨機性，導(dǎo)致網(wǎng)絡(luò)輸出結(jié)果不穩(wěn)定〔9〕。為此，提出基于遺傳算法GA優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的方法。通過遺傳算法全局最優(yōu)的功能很好的彌補BP神經(jīng)網(wǎng)絡(luò)的上述缺陷，優(yōu)化其連接權(quán)值和閾值，極大提高BP神經(jīng)網(wǎng)絡(luò)的穩(wěn)定性。

以雅康高速大渡河興康特大懸索橋雅安岸邊坡抗滑樁開挖爆破為依托，建立抗滑樁開挖爆破參數(shù)計算的基于GA改進(jìn)BP神經(jīng)網(wǎng)絡(luò)模型，針對本項目和其它工程已取得良好爆破效果的數(shù)據(jù)進(jìn)行快速學(xué)習(xí)，優(yōu)化抗滑樁開挖爆破參數(shù)。

2GA-BP神經(jīng)網(wǎng)絡(luò)模型

2.1BP神經(jīng)網(wǎng)絡(luò)設(shè)計

BP神經(jīng)網(wǎng)絡(luò)模型是一種有導(dǎo)學(xué)習(xí)算法，也稱誤差反向傳播算法〔9〕。在正向傳播過程中，每一層神經(jīng)元的狀態(tài)只影響到下一層神經(jīng)元網(wǎng)絡(luò)，當(dāng)網(wǎng)絡(luò)模型實際輸出與期望輸出有誤差，則轉(zhuǎn)入反向傳播過程，通過修改各層神經(jīng)元權(quán)值，再進(jìn)行正向傳播過程，經(jīng)過正反傳播兩個過程的反復(fù)應(yīng)用使得誤差最小，以使模型達(dá)到最優(yōu)。

(1)BP網(wǎng)絡(luò)模型輸入、輸出參數(shù)

抗滑樁孔開挖爆破設(shè)計參數(shù)和影響因素較多，考慮到本工程實際情況，為了減少爆破對圍巖的損傷以及減小振動，在開挖過程中采用光面爆破和分段延時掏槽爆破的方案。在爆破參數(shù)設(shè)計中，根據(jù)不同的巖石性質(zhì)，選取不同的炸藥單耗。為實現(xiàn)爆破后續(xù)人工開挖的方便和滿足施工周期要求，平均線性超挖和線性欠挖、開挖進(jìn)尺等也是需要考慮的因素。

綜上所述，結(jié)合本例實際工程情況，選取輸入?yún)?shù)為平均線性超挖W1(m)、平均線性欠挖W2(m)、抗滑樁孔的斷面面積A(m2)、實際進(jìn)尺L1(m)以及巖石f值，輸出參數(shù)為設(shè)計進(jìn)尺L2(m)、炸藥單耗q(kg·m-3)、周邊孔孔距E(m)、光爆層厚度d(m)、輔助孔孔距a(m)和掏槽孔孔距b(m)。

(2)網(wǎng)絡(luò)層數(shù)

由Kolmogorov定理可知〔10〕，一個三層的神經(jīng)網(wǎng)絡(luò)可以實現(xiàn)逼近任何一個函數(shù)，本文選擇有一個隱含層的BP神經(jīng)網(wǎng)絡(luò)，即網(wǎng)絡(luò)包含輸入層、隱含層和輸出層，選取激活函數(shù)均為Sigmoid函數(shù)，即f(x)=1/(1+e-x)。

(3)隱含層節(jié)點數(shù)

隱含層節(jié)點數(shù)的選擇一般有三種方法〔11〕：

H=2I+1

(1)

(2)

H=log2I,I∈(0.02I,4I)

(3)

式中：H為隱含層節(jié)點數(shù)，I為輸入層節(jié)點數(shù)，O為輸出層節(jié)點數(shù)，?為常數(shù)。但實際建模時，主要是通過網(wǎng)絡(luò)模型對學(xué)習(xí)樣本和測試樣本的誤差交叉評價，并采用試錯法選取。經(jīng)過反復(fù)試驗，隱含層節(jié)點數(shù)選為7，其拓?fù)浣Y(jié)果見圖1。

圖1　神經(jīng)網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)圖Fig.1　Topology structure of neural network

(4)學(xué)習(xí)率

在網(wǎng)絡(luò)模型設(shè)計中，學(xué)習(xí)速率的選取是影響收斂速度以及訓(xùn)練結(jié)果的一個很重要的因素。學(xué)習(xí)速率足夠小，雖然總能夠使訓(xùn)練網(wǎng)絡(luò)滿足精度要求，但耗時較長；學(xué)習(xí)速率較大，則可能導(dǎo)致訓(xùn)練過程不穩(wěn)定。因此，本文通過不斷重復(fù)試驗，選取學(xué)習(xí)率η為0.045。

(5)訓(xùn)練誤差

(4)

式中：djl、yjl分別為輸入樣本為l時對應(yīng)的期望輸出和實際輸出。

2.2遺傳算法對BP網(wǎng)絡(luò)權(quán)值和閾值的設(shè)計

用遺傳算法GA優(yōu)化BP神經(jīng)網(wǎng)絡(luò)連接權(quán)值和閾值主要涉及以下三個步驟：基因表達(dá)，即基因的編碼方式；適應(yīng)度函數(shù)的選取；遺傳操作(主要包括選擇、交叉和變異)的確定。

(1)編碼。為了提高運算精度和計算速度，省去二進(jìn)制和十進(jìn)制之間的解碼過程，直接采用實數(shù)編碼。由圖1 可知GA-BP的神經(jīng)網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)為5-7-6，因此采用遺傳算法對連接權(quán)值和閾值進(jìn)行編碼的長度R=5×7+7×6+7+6=90。

(2)適應(yīng)度函數(shù)。適應(yīng)度函數(shù)是遺傳算法中評價種群個體遺傳至下一代概率大小的關(guān)鍵依據(jù)，通過比較群體中每個個體的適應(yīng)度可以判斷其達(dá)到或接近全局最優(yōu)解的程度〔13〕。適應(yīng)度越高的個體，離全局最優(yōu)解越近，反之則越遠(yuǎn)。由公式(4)可知,BP神經(jīng)網(wǎng)絡(luò)將均方誤差作為訓(xùn)練誤差，誤差越小越好。采用將個體訓(xùn)練誤差的倒數(shù)作為適應(yīng)度函數(shù)，當(dāng)適應(yīng)度最大時，表明優(yōu)化的連接權(quán)和閾值達(dá)到最優(yōu)，表達(dá)式如下所示：

f(i)=1/Ei

(5)

式中：f(i)即為種群中第i條染色體的適應(yīng)度值；Ei為對應(yīng)第i條染色體進(jìn)行優(yōu)化BP網(wǎng)絡(luò)的連接權(quán)和閾值時的訓(xùn)練誤差。

(3)遺傳操作

① 選擇操作。主要是以適應(yīng)度值為依據(jù)，適應(yīng)度高的個體被選擇的概率較高，反之較低。通過每個個體的適應(yīng)度值計算個體被選擇的概率，具體如式(6)所示：

(6)

式中：Pi為第i個個體被選擇的概率；fi為公式(5)中的第i個個體的適應(yīng)度值。

② 交叉操作。交叉操作是遺傳算法全局搜索功能的關(guān)鍵操作，鑒于上述采用實數(shù)編碼，因此交叉操作選擇算術(shù)交叉法〔12〕。假設(shè)種群中x1和x2為父代個體，則通過交叉操作產(chǎn)生的子代個體x1′和x2′如下：

(7)

③ 變異操作。在本文中，變異操作和交叉操作結(jié)合使用，變異操作的目的是提高遺傳算法在優(yōu)化連接權(quán)和閾值的局部搜索功能，同時保持遺傳種群的多樣性。因此結(jié)合上述設(shè)計，本文采用均勻變異操作。

2.3網(wǎng)絡(luò)模型的學(xué)習(xí)算法

網(wǎng)絡(luò)模型學(xué)習(xí)算法如下所示：

(1)網(wǎng)絡(luò)初始化。根據(jù)已確定的網(wǎng)絡(luò)結(jié)構(gòu)，采用遺傳算法編碼，并確定初始種群，通過反復(fù)選擇、交叉、變異獲得網(wǎng)絡(luò)初始權(quán)值和閾值。

(2)獲得的權(quán)值和閾值賦予BP神經(jīng)網(wǎng)絡(luò)，依次輸入8個學(xué)習(xí)樣本。設(shè)當(dāng)前輸入樣本為第p個樣本。

(3)依次計算各層的輸出。

第二層：

(8)

第三層：

(9)

(4)計算各層反傳誤差。

由BP算法可知，誤差反向傳播，所以首先計算第三層：

δjk=(dlp-ylp)ylp(1-ylp),(l=0,1,…,4)

(10)

再計算第二層：

(11)

(5)按權(quán)值修正公式修正各層的權(quán)值和閾值。

3實例計算

3.1網(wǎng)絡(luò)模型的訓(xùn)練和預(yù)測

為驗證GA-BP神經(jīng)網(wǎng)絡(luò)模型的合理性，以在建的雅康高速大渡河興康特大懸索橋雅安岸邊坡抗滑樁孔開挖爆破為例進(jìn)行分析。選取本例和其它工程已有的8組爆破效果較優(yōu)的輸入、輸出參數(shù)作為網(wǎng)絡(luò)模型的學(xué)習(xí)樣本〔13-14〕，如表1所示。當(dāng)網(wǎng)絡(luò)學(xué)習(xí)誤差ε小于0.001時，結(jié)束模型學(xué)習(xí)。

將輸入?yún)?shù)和輸出參數(shù)分別加載至網(wǎng)絡(luò)模型兩端進(jìn)行學(xué)習(xí)，圖2給出了網(wǎng)絡(luò)訓(xùn)練實際輸出與期望目標(biāo)的相關(guān)系數(shù)，可以看出網(wǎng)絡(luò)模型訓(xùn)練后，網(wǎng)絡(luò)模型的輸出值與期望目標(biāo)的線性相關(guān)系數(shù)為0.9862，表明本文所建立的網(wǎng)絡(luò)模型具有較好的擬合效果，可以達(dá)到工程實際所需。

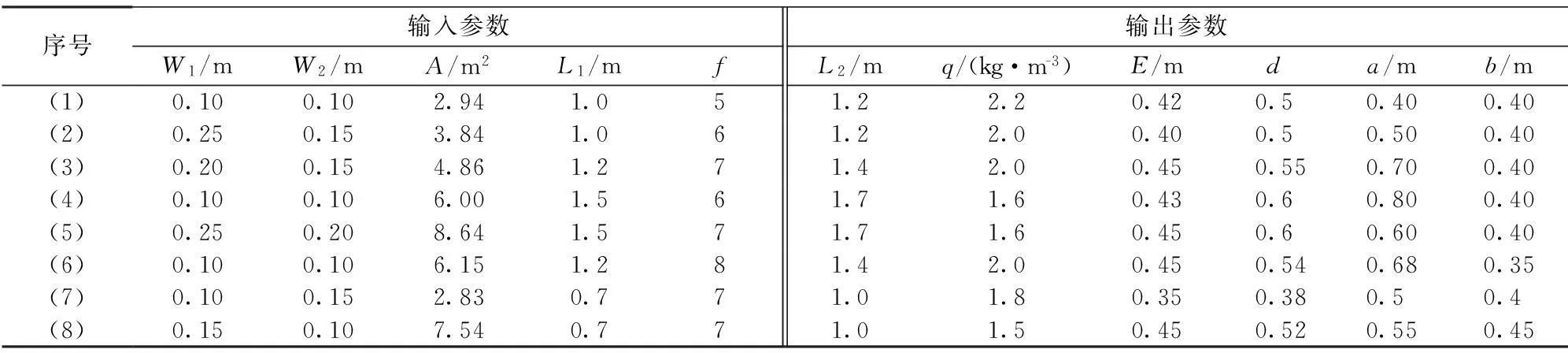
表1　網(wǎng)絡(luò)學(xué)習(xí)樣本

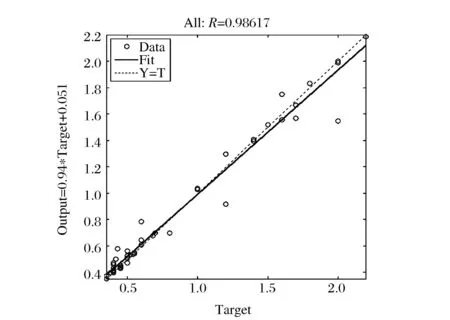
圖2　網(wǎng)絡(luò)訓(xùn)練實際輸出與期望目標(biāo)相關(guān)系數(shù)Fig.2　Correlation coefficient of network training actual output and the expected target

為了驗證訓(xùn)練結(jié)束網(wǎng)絡(luò)模型的可靠度，同時比較基于遺傳算法改進(jìn)的BP神經(jīng)網(wǎng)絡(luò)與原有BP神經(jīng)網(wǎng)絡(luò)的預(yù)測精度，另選取其他工程不同樁孔尺寸、不同巖體性質(zhì)且有良好爆破效果的3組輸入、輸出參數(shù)樣本(表2)作為模型預(yù)測樣本〔15〕，預(yù)測結(jié)果見表3、表4。其中表3為一般BP神經(jīng)網(wǎng)絡(luò)的預(yù)測結(jié)果，表4 為GA-BP神經(jīng)網(wǎng)絡(luò)的預(yù)測結(jié)果。

由表3和表4對比可以看出，基于遺傳算法改進(jìn)后的BP神經(jīng)網(wǎng)絡(luò)預(yù)測精度均高于原始BP神經(jīng)網(wǎng)絡(luò)的預(yù)測精度。GA-BP神經(jīng)網(wǎng)絡(luò)預(yù)測結(jié)果的最大平均相對誤差為4.0%，一般BP網(wǎng)絡(luò)的預(yù)測結(jié)果最大平均相對誤差為7.4%，由此可以看出原始BP網(wǎng)絡(luò)預(yù)測結(jié)果的離散程度較大，改進(jìn)后的BP網(wǎng)絡(luò)的預(yù)測平均相對誤差更小，預(yù)測結(jié)果也更穩(wěn)定。

表2　網(wǎng)絡(luò)模型檢驗樣本

表3　一般BP神經(jīng)網(wǎng)絡(luò)預(yù)測結(jié)果

表4　GA-BP神經(jīng)網(wǎng)絡(luò)預(yù)測結(jié)果

注：X為計算值， m；Δ為絕對誤差， m；ε為相對誤差， %。

3.2現(xiàn)場試驗

為了進(jìn)一步檢驗所建立GA-BP網(wǎng)絡(luò)模型的效果，以雅康高速大渡河興康特大懸索橋雅安岸邊坡抗滑樁開挖為例，對未開挖的抗滑樁孔利用上述網(wǎng)絡(luò)模型進(jìn)行爆破參數(shù)設(shè)計。經(jīng)現(xiàn)場調(diào)查，確定所需設(shè)計的輸入?yún)?shù)向量(0.20，0.15，4.15，1.20，5.00)，將向量加載至模型的輸入端進(jìn)行仿真，可以得到輸出向量(1.30，1.70，0.45，0.58，0.60，0.40),即設(shè)計進(jìn)尺為1.3m，炸藥單耗為1.70 kg/m3，周邊孔孔距為0.45m，光爆層厚度為0.58m，輔助孔孔距0.60m，掏槽孔孔距0.40m。

將GA-BP神經(jīng)網(wǎng)絡(luò)模型仿真的爆破設(shè)計參數(shù)進(jìn)行現(xiàn)場試爆，開挖爆破試驗之后，巖體爆渣塊度比較均勻，大塊率較低，一般的塊體尺寸在10cm～25cm，便于后續(xù)清渣。同時，為了判斷爆破過程對周邊抗滑樁孔的影響，對與待爆抗滑樁孔水平距離最近的抗滑樁孔孔底基巖面和孔壁處進(jìn)行聲波檢測和爆破振動監(jiān)測，聲波測試結(jié)果見表5。

表5　聲波測試結(jié)果

注：測點1～4為樁底基巖面聲波波速測試；測點5～8為樁底孔壁聲波波速測試。

由表5可以看出，樁孔開挖爆破后各測點位置的聲波速度下降率均小于10%，平均下降率為5.7%，說明樁孔開挖爆破對樁孔圍巖(基巖)的完整性、連續(xù)性沒有造成明顯影響。同時孔底爆破振動監(jiān)測結(jié)果表明，爆破振動速度最大值為5.9cm/s，滿足振動最大速度不超過10.0cm/s 的設(shè)計要求。因此本文建立的GA-BP神經(jīng)網(wǎng)絡(luò)模型滿足工程要求，可以用來指導(dǎo)實際抗滑樁孔開挖爆破參數(shù)設(shè)計。

4結(jié) 論

(1)抗滑樁孔開挖爆破參數(shù)設(shè)計影響因素較多，GA-BP神經(jīng)網(wǎng)絡(luò)充分利用GA算法的全局搜索功能和BP網(wǎng)絡(luò)強大非線性映射、自學(xué)習(xí)、自適應(yīng)能力等特點，按網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)為5-7-6建立的三層GA-BP神經(jīng)網(wǎng)絡(luò)模型，通過對樣本的學(xué)習(xí)相關(guān)系數(shù)達(dá)到0.9862，預(yù)測輸出結(jié)果精度較高，方法可行。

(2)采用基于GA算法改進(jìn)的BP神經(jīng)網(wǎng)絡(luò)模型對爆破參數(shù)進(jìn)行設(shè)計，計算結(jié)果表明，其預(yù)測結(jié)果的相對誤差比一般BP網(wǎng)絡(luò)低，預(yù)測精度較高且網(wǎng)絡(luò)模型更穩(wěn)定。同時GA-BP神經(jīng)網(wǎng)絡(luò)方法利用已有爆破經(jīng)驗數(shù)據(jù)和工程地質(zhì)條件，有效避免了因設(shè)計者爆破理論和經(jīng)驗不足導(dǎo)致的爆破參數(shù)設(shè)計質(zhì)量參差不齊的情況。

(3)通過對雅安岸邊坡抗滑樁孔開挖爆破參數(shù)預(yù)測的現(xiàn)場試驗結(jié)果表明，利用GA-BP神經(jīng)網(wǎng)絡(luò)模型設(shè)計爆破參數(shù)，滿足抗滑樁爆破施工需要，可以為抗滑樁孔開挖爆破參數(shù)設(shè)計提供依據(jù)。

參考文獻(xiàn)(References)：

〔1〕 程遠(yuǎn)學(xué)，程康，周子然，等. 人工挖孔樁爆破開挖技術(shù)探討[J]. 土工基礎(chǔ)，2007，21(4):5-6.

CHENG Yuan-xue, CHENG Kang, ZHOU Zi-ran, et al. Discussion of explosive excavation technique of hand-dug pile [J]. Soil Eng. and Foundation，2007,21(4):5-6.

〔2〕 張成良，楊陽，梁開水，等. 巖壁梁爆破參數(shù)優(yōu)化的神經(jīng)網(wǎng)絡(luò)模型[J]. 工程爆破，2006，12(1):22-26.

ZHANG Cheng-liang, YANG Yang, LIANG Kai-shui, et al. Neural network model of blasting parameters optimization of crane beam at rock wall[J]. Engineering blasting,2006,12(1):22-26.

〔3〕 張繼春，蔡德所，胡鐵松. 基于神經(jīng)網(wǎng)絡(luò)理論的巖體爆破效應(yīng)預(yù)測[J]. 東北大學(xué)學(xué)報，1995, 16(增刊):101-106.

ZHANG Ji-chun, CAI De-suo, HU Tie-song. Rock blasting effect forecast based on neural network theory [J]. Journal of Northeast University, 1995, 16( Sup. ): 101-106.

〔4〕 張磊. 入巖控制爆破技術(shù)在鐵路橋梁挖孔樁中的應(yīng)用[J]. 山西建筑，2011，37(27):193-194.

ZHANG Lei. The application of controlled blasting into the rock technology in railway bridge digging piles [J].Shanxi Architecture, 2011,37(27):193-194.

〔5〕 林文強，蘇陽，歐陽衡. 人工挖孔樁工程孔內(nèi)基巖爆破設(shè)計和施工簡介[J]. 水運工程，2001(2):56-58.

LIN Wen-qiang, SU Yang, OUYANG Heng. Design and construction of in-hole base rock explosive for artificial excavation-hole pile engineering [J].Port & Waterway Engineering,2001(2):56-58.

〔6〕 劉召芹. 光面爆破技術(shù)在人工挖孔樁中的應(yīng)用[J]. 西部探礦工程，2001，69(2):89-90.

LIU Zhao-qin. Smooth blasting technology applied in the manual excavating pile [J].West-china Explosive Engineering,2001,69(2):89-90.

〔7〕 柴毅，尹宏鵬，李大杰，等. 基于改進(jìn)遺傳算法的BP神經(jīng)網(wǎng)絡(luò)自適應(yīng)優(yōu)化設(shè)計[J]. 重慶大學(xué)學(xué)報(自然科學(xué)版)，2007，30(4):91-96.

CHAI Yi, YIN Hong-peng, LI Da-jie, et al. Self-adaptation optimize BP neural design based on the genetic algorithms [J]. Journal of Chongqing University (Natural Science Edition), 2007,30(4):91-96.

〔8〕 姚金階，朱以文. 巖體爆破參數(shù)設(shè)計的神經(jīng)網(wǎng)絡(luò)模型[J]. 爆破，2005，22(2):34-37.

YAO Jin-jie, ZHU Yi-wen. The neural network model of rock blasting parameters design [J].Blasting,2005,22(2):34-37.

〔9〕 劉慶，張光權(quán)，吳春平，等. 基于BP神經(jīng)網(wǎng)絡(luò)模型的爆破飛石最大飛散距離預(yù)測研究[J]. 爆破，2013，30(1):115-118.

LIU Qing, ZHANG Guang-quan,WU Chun-ping, et al. Research on maximum distance prediction of blast fly rock based on BP neutral work [J].Blasting,2013,30(1):115-118.

〔10〕 鄭長青，陳慶壽，徐海波，等. 基于神經(jīng)網(wǎng)絡(luò)的臺階爆破參數(shù)優(yōu)化設(shè)計[J]. 爆破，2008，25(3):22-25.

ZHENG Chang-qing, CHEN Qing-shou, XU Hai-bo, et al. Bench blasting design and optimization based on neural network [J]. Blasting,2008,25(3):22-25.

〔11〕 楊建剛. 人工神經(jīng)網(wǎng)絡(luò)實用教程[M]. 杭州：浙江大學(xué)出版社，2002.

YANG Jian-gang. Practical artificial neural network tutorial[M]. Hangzhou: Zhejiang University Press, 2002.

〔12〕 陳德志，朱瑞賡，徐順香. 基于BP神經(jīng)網(wǎng)絡(luò)的路塹爆破對鄰近民房安全預(yù)測的研究[J].巖石力學(xué)與工程學(xué)報，2002，21(S2):2554-2557.

CHEN De-zhi, ZHU Rui-geng, XU Shun-xiang. BP neural network study on safety prediction for civil houses adjacent to cutting blasting [J]. Chinese Journal of Rock Mechanics and Engineering, 2002,21(S2):2554-2557.

〔13〕 范睿，李國斌，景韶光. 基于實數(shù)編碼遺傳算法的混合神經(jīng)網(wǎng)絡(luò)算法[J]. 計算機仿真，2006，23(1):161-162.

FAN Rui, LI Guo-bin, JING Shao-guang. A method of mixed neural network based on real-coded genetic algorithm [J]. Computer simulation, 2006,23(1):161-162.

〔14〕 羅學(xué)東，范新宇，代貞偉，等. BP神經(jīng)網(wǎng)絡(luò)模型在露天礦爆破振動參數(shù)預(yù)測中的應(yīng)用及修正[J]. 中南大學(xué)學(xué)報(自然科學(xué)版)，2013，44(1):5020-5024.

LUO Xue-dong, FAN Xin-yu, DAI Zhen-wei, et al. BP neural network application and model modification in prediction of open-pit mine blasting vibration parameters [J]. Journal of Central South University, 2013,44(1):5020-5024.

〔15〕 爆破安全規(guī)程 GB 6722-2014[S]. 北京：中國標(biāo)準(zhǔn)出版社，2014.

Safety regulations for blasting GB 6722-2014[S]. Beijing: China Standards Press, 2014.

Application of BP neural network improved by GA in blasting excavation design of slide-resistant pile hole

YUE Heng， HAN Xiang-yu， ZHANG Ji-chun， PAN Qiang， LI Peng-chuan， YANG Tao

(School of Civil Engineering, Southwest Jiaotong University, Chengdu 610036, China)

ABSTRACT：Currently, the pile holes are excavated mainly relying on the engineering analogy, but the blasting parameters designed by different theories and experience and the effect of blasting are different. Therefore, BP neural network improved by genetic algorithm was provided and the model of optimization of blasting parameters was set up. The sample data obtained from good blasting effect and geology of practical engineering could be used, and GA could make up the defect of BP neural network which was not stable through optimizing the threshold and weight of BP neural network, and the purpose of obtaining the better blasting parameters was achieved. The practice showed that relative errors of prediction of GA-BP neural network were fewer than the general BP neural network, and it achieved a good result after field test using the optimized blasting parameters. GA-BP neural network model was well applied in the blasting parameters design of excavation of slide-resistant pile hole, it was feasible and could be used to guide the construction of blasting.

KEY WORDS:Blasting parameters optimization; BP neural network; GA; Field test; Pile hole excavation; Blasting excavation

文章編號：1006-7051(2016)02-0028-06

收稿日期：2015-10-15

基金項目：國家自然科學(xué)基金項目(41272321)

作者簡介：岳 衡(1993-)，男，碩士，主要從事工程控制爆破方面的研究。E-mail: yueh0829@sina.com通訊作者：張繼春(1963-)，男，博士、教授、博導(dǎo)，主要從事工程爆破和爆炸防護(hù)方面的教學(xué)與科研工作。E-mail: jczhang2004@126.com

中圖分類號：TD235.1； U25

文獻(xiàn)標(biāo)識碼：A

doi：10.3969/j.issn.1006-7051.2016.02.006