組合核RVM在CPI預測中的應用研究

李昌良，江　燕，王殿君，韓繼光

(1.昆明理工大學　a.質量發展研究院； b.信息工程與自動化學院，昆明　650093；2.山西財經大學 會計學院，太原　030006； 3.云南農業大學 機電工程學院，昆明　650201)

?

組合核RVM在CPI預測中的應用研究

李昌良1a，江燕2，王殿君1b，韓繼光3

(1.昆明理工大學a.質量發展研究院； b.信息工程與自動化學院，昆明650093；2.山西財經大學 會計學院，太原030006； 3.云南農業大學 機電工程學院，昆明650201)

摘要：針對傳統預測模型訓練時間長、誤差大的缺陷，提出高可靠的組合核相關向量機模型用于CPI預測。構建組合核相關向量機預測模型，根據我國1987年1月至2015年2月的CPI月度數據，得到CPI的回歸預測曲線，再與支持向量機和單核相關向量機進行對比。仿真模擬表明：組合核相關向量機預測模型預測CPI的平均誤差可控制在1%以內，運行時間為1.35 s，預測結果良好。

關鍵詞：組合核；相關向量機；CPI

一、引言

居民消費價格指數(CPI)，是衡量居民購買生活相關產品及服務價格波動的宏觀經濟指標，通常用以反映通貨水平，與貨幣供應量、國內生產總值、匯率、投資與消費、需求和供給等有著極其重要的聯系，它們之間相互依存相互作用。它既是宏觀經濟運行的“晴雨表”，也通過價格變化影響人民生活水平。全球經濟復蘇乏力，我們國家自2014年9月CPI重返“1時代”，也面臨著很大的經濟下行壓力，因而為保持價格平穩，預測CPI異常重要。

目前，研究和預測CPI問題的方法主要有經典時間序列方法和智能算法。經典時間序列方法如ARMA、ARCH、BVAR等大多是線性模型，而這些模型通常要求數據具有正態性和平穩性，因此對于如同CPI這類非線性非平穩時間序列的預測存在著一定的局限性[1-2]。為克服以上不足，一些學者引入智能算法進行時間序列的分析，其中支持向量機可以解決小樣本、非線性、高維數、局部極小點等[3-5]實際問題，常用于金融時間序列的預測[6-8]。但支持向量機的應用需要在馬瑟條件下選擇最優參數，且算法復雜、運算速度較慢、預測精度不高；因此 Zhang Lei等將核函數與相關向量機結合研究、診斷、預測電力系統故障[9-11]，韓敏等運用相關向量機進行時間序列預測，通過相關向量機自選最優參數，取得了較好的效果[12]。

上述成果為本文研究提供了極好的參考價值和理論依據。同時，組合核相關向量機也恰好彌補了上述方法的不足，且可以利用相關向量機的概率預測優勢得到其他預測模式無法得到的預測誤差范圍[10]。基于此，本文選用組合核相關向量機進行居民消費價格指數的預測。

二、組合核RVM 的CPI預測模型

基于上述CPI的預測特點，結合2001年Michael E Tipping博士基于貝葉斯概率和最大似然等相關理論建立組合核RVM 的CPI預測模型，通過最大化邊際似然函數獲取關聯向量和權重。權重和核函數充分描述了相關向量機的結構。核函數是指一組輸入的數據投影到一個高維特征空間的基函數。

(一)RVM 算法

此處將具系統高度非線性的CPI數據進行外推數據重組處理，假定CPI訓練樣本總數為N，則N=(x1,x2,x3,…,xN)， 進一步對訓練樣本集進行處理，形成M列數據，一共產生M-1列測試集，第M列為訓練集：

(1)

(2)

其中，k(x,xi)是核函數，wi是回歸系數。對于整個樣本集的似然函數為：

(3)

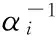
(4)

其中，α=[α0,α1,…,αN]T是超參數，每個超參數αi都有對應的wi。由貝葉斯公式即可得到權重后驗分布的數學表達式：

p(t|W,α,σ2)=

(5)

m=σ-2∑ΦTt

(6)

∑=(σ-2ΦTΦ+A)-1

(7)

其中，A=diag(α1,α2,…,αN)。并通過集成權重獲得最大似然函數：

(8)

其中，協方差可表示C=σ2I+ΦA-1ΦT。分別對α和σ2求偏導，令其等于0，可得：

(9)

(10)

其中mi是第i個元素，且γi=1-αi∑ii，∑ii是矩陣∑的第i個對角元。

相關向量機不斷重復運算，同時不斷更新m和∑，直到滿足收斂要求或達到最大迭代次數。也就是說在不斷計算過程中，大部分權重趨近于0，產生核函數矩陣項，而其中大部分不會參與到實際預測計算中[11]。

(二)核函數的選取

滿足 Mercer 定理的函數都可以作為核函數。常見的核函數有高斯徑向基核函數和多項式核函數。

(11)

K2(x,x′)=((x,x′)+1)d,d=1,2,…

(12)

大部分實際問題的數據均服從高斯分布，因此常選用高斯徑向基核函數作為RVM的核函數。徑向基核函數屬于典型的局部核函數，而多項式核函數則是典型的全局核函數；多項式核函數具有較強的推廣能力，而徑向基核函數具有較強的學習能力。因此選取高斯徑向基核函數和多項式核函數構成組合核函數用于RVM。

結合式(10)、(11)有組合核函數：

K(x,x′)=λK1(x,x′)+(1-λ)K2(x,x′)

其中，0≤λ≤1；當λ=0或λ=1時，組合核函數變成單一核函數；λ越大則高斯徑向基核函數占比越大，多項式核函數占比越小。

三、我國CPI預測仿真實驗

通過國家統計局網站選取我國1987年1月至2015年2月的CPI月度的338組數據進行實驗，圖1是我國此階段的CPI原始數據，可以看出從1987年開始居民消費價格指數快速增長，每年平均增長20%，直到1999年底；2000年到2006年CPI出現小幅波動，但還是屬于比較正常的現象；2007年以來我國由于受美國次貸危機的影響，居民消費價格指數出現大幅波動，尤其2009年居民消費價格指數大幅下滑；2010年以來又大幅上漲，這是由于前期政府4萬億元投資顯現，拉動CPI上揚；2012年下半年由于政府穩健的貨幣政策和4萬億元刺激的減弱，居民消費價格指數保持在合理區間，說明經濟環境整體運行良好。為驗證本文所提出的核函數的有效性，將組合核相關向量機與模糊神經網絡、支持向量機進行實例比較分析。數據集包含338個樣本，其中288個樣本為訓練集，50個樣本為測試集。實驗表明，令M=10個因素數為輸入值，第11個因素數為輸出值時，誤差最小。

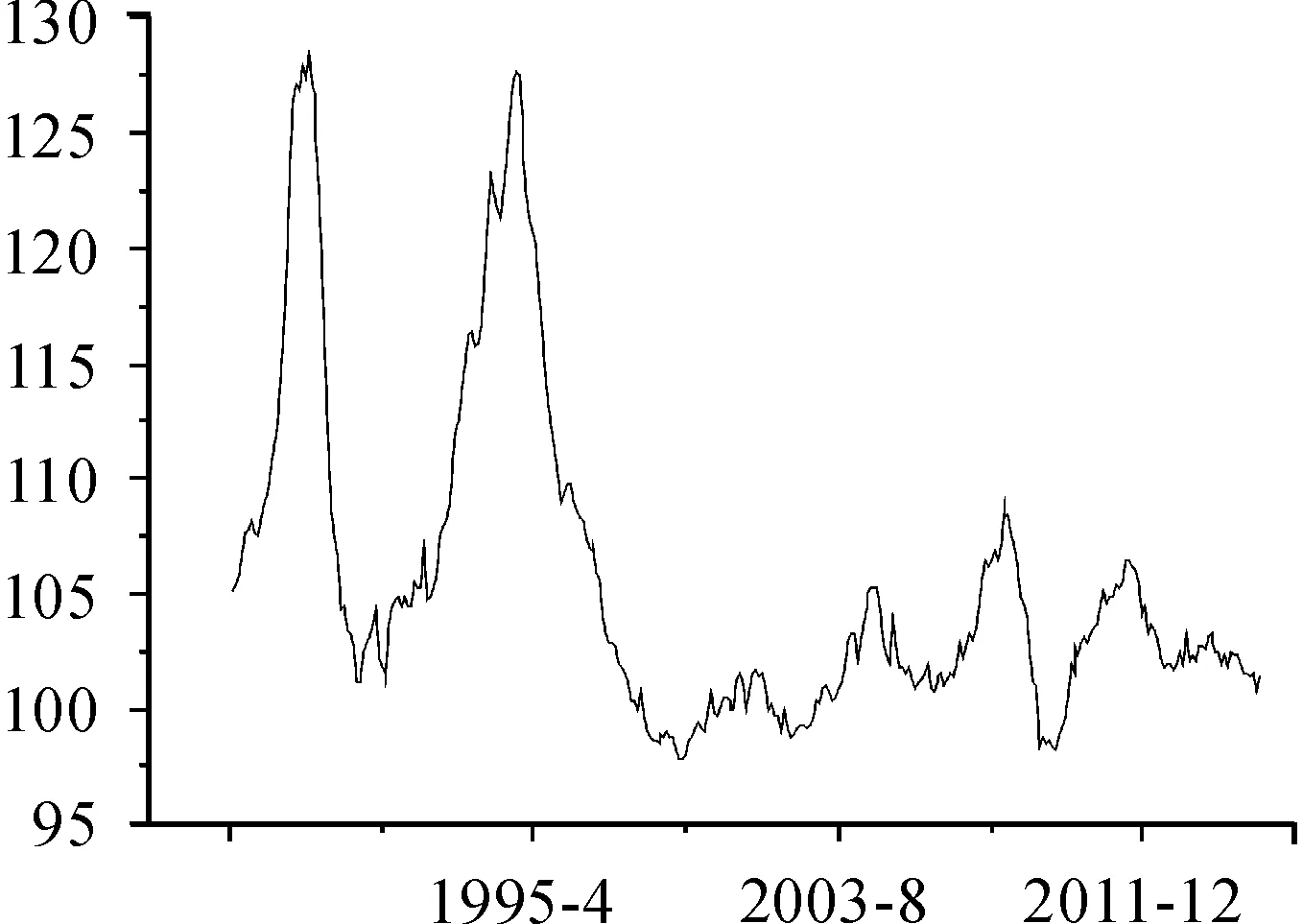
圖1　我國1987年1月至2015年2月CPI原始數據

(一)核函數參數選取

針對核函數k(x,x′)，進行核函數參數選取,令σ=0.7，d=2[12]。則核函數成為：

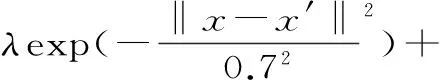
(1-λ)((x,x′)+1)2

(12)

其中λ∈[0.1,0.9]，按照步長為0.1，對λ進行確定，則關于參數λ與參數生成時間和誤差的關系如表1所示。

從表1可以看出，隨著λ的增大，誤差水平總體不斷增大，噪聲水平先增大后減小，運行時間誤差最小。因此選擇λ=0.1，則核函數為：

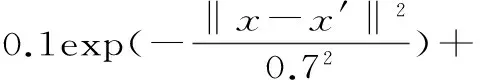
0.9((x,x′)+1)2

(13)

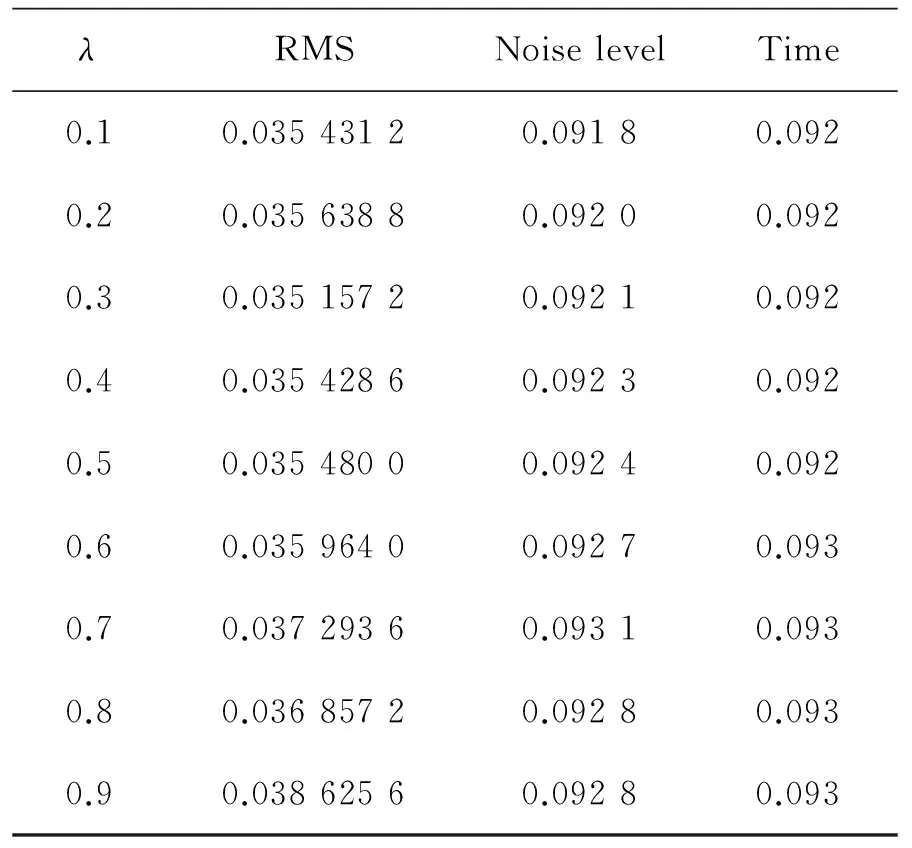
表1　參數選擇示意表

(二)結果分析

按照上述要求，用Matlab編制仿真實驗程序，選定參數N=300、noise=0.1、width=3、maxIts=1 200，其中支持向量機和單核相關向量機的核函數選擇kernel=gauss，相關向量機組合核函數選擇kernel=gauss+poly(如式(11))進行運行。通過前面的3種預測方法得出50個CPI預測數據，3種方法的預測結果如圖2，其中SVM表示支持向量機CPI回歸預測、RVM代表單核相關向量機CPI回歸預測、CK-RVM代表組合核相關向量機CPI回歸預測。可以看出支持向量機的CPI預測準確度明顯小于單核相關向量機CPI預測準確度和組合核相關向量機CPI回歸預測準確度，且由于相關向量機可以產生CPI預測誤差范圍，組合核相關向量機CPI回歸預測誤差范圍最小，體現出組合核相關向量機CPI回歸預測最為準確。

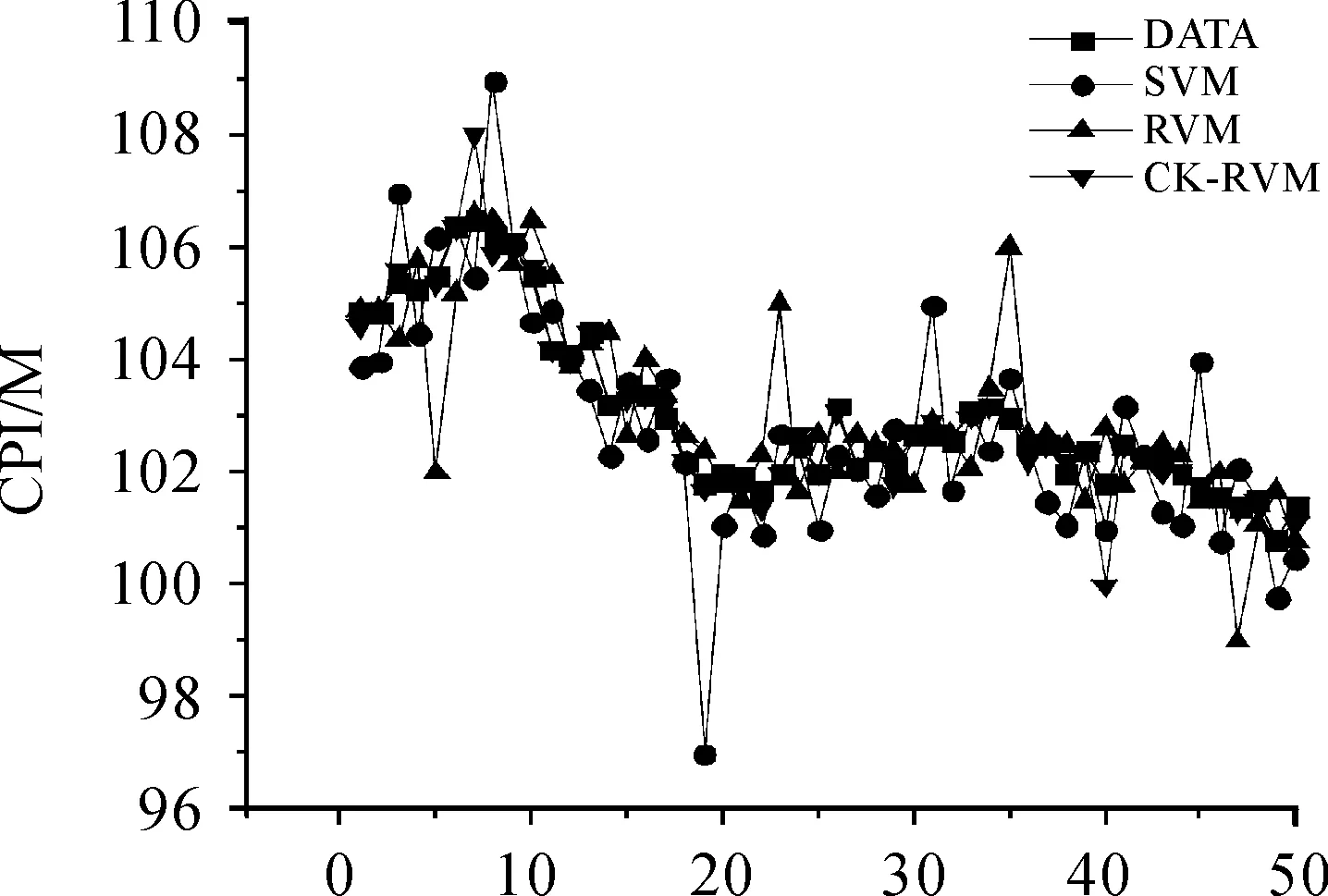
圖2　3種方法回歸預測示意圖

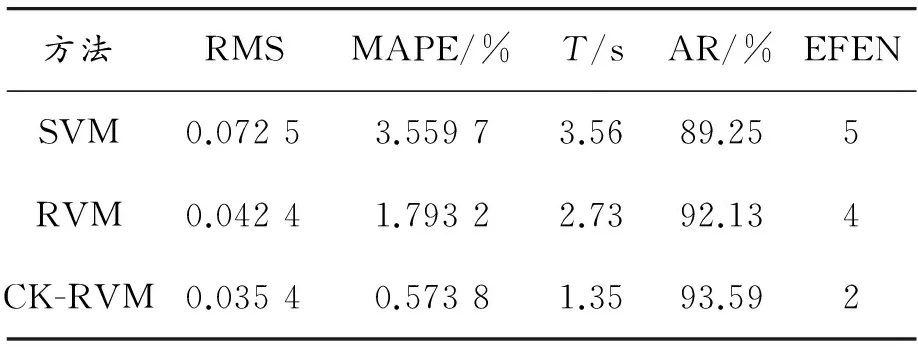
3種方法比較參數為：回歸測試誤差(Regression test error，RMS)、標準均方根誤差(Normalized root mean square error，NRMSE)、程序運行時間(Time，T)、正確率(Accuracy rate，AR)、超出預測誤差個數(Exceeding the forecast error number，EFEN)。通過表2可以看出用組合核函數的相關向量機運行時間最短，但其CPI回歸測試誤差最低，標準均方根誤差小于1%，測試結果的準確度SVM

表2　3種方法回歸誤差對比

四、結語

通過預測，發現CPI在近幾個月保持在1%左右，總體來說表現良好，但增速略有放緩，這并不是說明CPI越低越好，CPI越低表明人們手中的資本價值越高，但CPI又不能太高。保持CPI在一個合理上漲空間是很棘手的事情，可以通過穩健的財政政策和積極的貨幣政策予以解決。

通過運用組合核相關向量機預測居民消費價格指數，可以提高預測效率和準確性。在核方法的算法中，核函數的選擇是核心部分，因此在具備馬瑟條件的情況下，將數據進行重組處理找到CPI數據自身之間的關系；先對數據進行排列訓練，再將具有較強推廣能力的多項式核函數與具有較強學習能力的徑向基核函數進行結合，選取最優核函數分配參數權重，進而預測我國CPI的發展趨勢。從圖2和表2可以看出，組合核相關向量機預測模型預測CPI的平均誤差可控制在1%以內，運行時間為1.35 s，預測值和統計值擬合較好，取得了良好的預測結果。但此方法在運用組合核函數進行CPI經濟預測過程中，組合核函數中λ的更進一步精確確定是作者后面研究的主要方向，比如可以運用交叉驗證或蟻群算法進行尋優確定。

參考文獻：

[1]李召輝.基于小波分析的CPI實證研究及預測[D].成都：西南財經大學,2011.

[2]戴穩勝,呂奇杰,David Pitt.金融時間序列預測模型——基于離散小波分解與支持向量回歸的研究[J].統計與決策,2007(14):4-7.

[3]TAY F E H,CAO L.Application of support vector machines in financial time series forecasting[J].Omega,2001,29(4):309-317.

[4]MOURA M D C,ZIO E,LINS I D,et al.Failure and reliability prediction by support vector machines regression of time series data[J].Reliability engineering,2011,96(11):1527-1534.

[5]ZHENG B,MYINT S W,THENKABAIL P S,et al.A support vector machine to identify irrigated crop types using time-series landsat NDVI data[J].International journal of applied earth observation & geoinformation,2015,34(1):103-112.

[6]楊新臣,吳仰儒.中國消費者物價指數預測——基于小波變換與支持向量回歸的分析[J].山西財經大學學報,2010(2):1-8.

[7]PREE H,HERWIG B,GRUBER T,et al.On general purpose time series similarity measures and their use as kernel functions in support vector machines[J].Information Sciences,2014,281:478-495.

[8]路世昌，趙博琦，畢建武.基于模糊信息粒化SVM時序回歸CPI預測[J].統計與決策,2015(14):82-84.[9]ZHANG L.Fault prognostic algorithm based on multivariate relevance vector machine and time series iterative prediction [J].Procedia engineering,2012,29:678- 686.[10]段青，趙建國，馬艷，等.優化組合核函數相關向量機電力負荷預測模型[J].電機與控制學報，2010，14(6):33-38.

[11]朱永利，尹金良.組合核相關向量機在電力變壓器故障診斷中的應用研究[J].中國電機工程學報，2013(22):68-74.

[12]韓敏，許美玲，穆大蕓.無核相關向量機在時間序列預測中的應用[J].計算機學報，2014(12):2427-2432.

[13]PSORAKIS I， DAMOULAS T， GIROLAMI M A． Multiclass relevance vector machines： an evaluation of sparsity and accuracy[J]．IEEE Transactions on Neural Networks， 2010，21(10)： 1588-1598.

[14]TOLAMBIYA A,PREM K K．Relevance vector machine with adaptive wavelet kernels for efficient image coding [J].Neurocomputing,2010,73:1417-1424.

[15]王煒，郭小明，王淑艷，等.關于核函數選取的方法[J].遼寧師范大學學報(自然科學版)，2008，31(1):1-4.

(責任編輯魏艷君)

Study on Application of Compounding Kernels RVM in Prediction of CPI

LI Chang-liang1a，JIANG Yan2，WANG Dian-jun1b，HAN Ji-guang3

(1.a.Institute of Quality Development; b. Institute of Information Engineering and Automation, Kunming University of Science and Technology, Kunming 650093, China;2.School of Accountancy, Shanxi University of Finance and Economics, Taiyuan 030006, China;3.School of Mechatronic Engineering, Yunnan Agricultural University, Kunming 650201, China)

Abstract:Traditional forecasting models have defects of needing long training time and producing more errors. This paper presents highly reliable nuclear relevance vector machine model used for the CPI forecasts. Based on the monthly historical data from January 1987 to February 2015 CPI, the paper builds a composite core relevance vector machine predictive model, forecasts regression curves by the CPI. Simulation shows that the combination of nuclear relevance vector machines prediction model can make the average error of the CPI controlled within 1%, and the running time is 1.35 s, so it achieved good results.

Key words:Compounding Kernels (CK); Relevance Vector Machines (RVM); CPI

收稿日期：2015-11-10

作者簡介：李昌良(1990—)，男，四川簡陽人，碩士研究生，研究方向：數據挖掘。

doi:10.3969/j.issn.1674-8425(s).2016.05.006

中圖分類號：F273.7

文獻標識碼：A

文章編號：1674-8425(2016)05-0048-05

引用格式：李昌良，江燕，王殿君，等.組合核RVM在CPI預測中的應用研究[J].重慶理工大學學報(社會科學)，2016(5):48-52.

Citation format：LI Chang-liang，JIANG Yan，WANG Dian-jun,et al.Study on Application of Compounding Kernels RVM in Prediction of CPI[J].Journal of Chongqing University of Technology(Social Science)，2016(5):48-52.