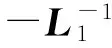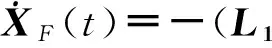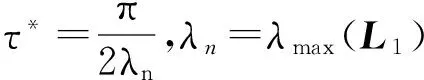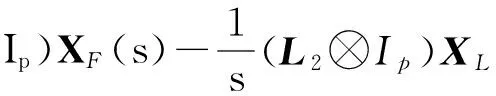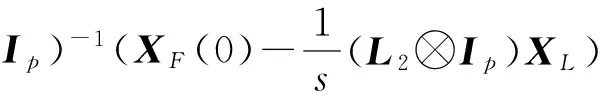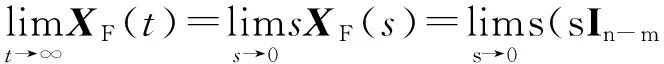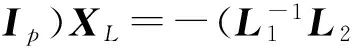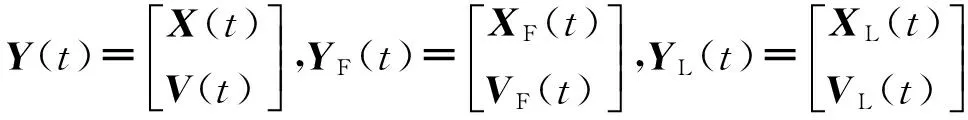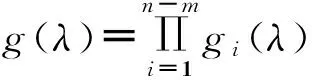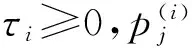含時延的多智能體系統的多靜態領導者包容控制

李　勃，陳增強*,，劉忠信，張　青

(1.南開大學計算機與控制工程學院，天津 300071；2.中國民航大學理學院，天津 300300)

?

含時延的多智能體系統的多靜態領導者包容控制

李勃1，陳增強*1,2，劉忠信1，張青2

(1.南開大學計算機與控制工程學院，天津 300071；2.中國民航大學理學院，天津 300300)

摘要：對基于有向固定拓撲的多靜態領導者的多智能體系統的包容控制問題進行研究。在系統中智能體之間信息傳遞存在固定通信時延的情況下，應用拉普拉斯變換技術分別研究一階和二階連續時間多智能體系統，通過對系統傳遞函數的穩定性分析而求取系統狀態穩定條件，并應用終值定理，最終得到了保證系統實現包容控制的時延限制條件，最后用仿真驗證了該結論的有效性。

關鍵詞:多智能體系統；包容控制；多靜態領導者；通信時延；終值定理

0引言

近幾年來，對多智能體系統控制的研究逐漸成為熱點。多智能體系統是人類在對自然界中的動物和鳥類集體運動的研究基礎上發展起來的，其在無人機的編隊控制、多機器人協同工作、通訊網絡的擁塞控制等領域有著非常廣泛的應用，推動著多智能體系統建模與分析的研究不斷向前發展。多智能體系統的控制目標主要包括智能體編隊、群集、聚集等，其中狀態一致性是研究的核心問題之一。多智能體系統的研究始于Reynolds等[1]提出的模仿動物集結的計算機模型，在此基礎上Vicsek等[2]從統計力學的角度提出一個非平衡多智能體系統模型，Jadbabaie等[3]對Vicsek模型線性化，從理論上研究了該模型的角度一致性問題。Moreau[4]和Ren等[5]將文獻[3]的結果推廣到有向網絡，得到了類似的收斂性結果。

自然中的群體運動通常都有一個或多個“領袖”，受其啟示，研究人員設計領航-跟隨控制方案來實現多智能體網絡的協調控制，根據領航者是否實際存在，可分為虛擬領航和實際領航，根據領航者的個數，可分為單領航和多領航情況。其中包容控制是多領航的一種典型情況，其本質是指一組跟隨者在多個領導者的引領下，從而到達并保持在由領導者所圍成的最小幾何空間(凸包)中運動。在實際應用中，包容控制具有大量的潛在應用。包容控制問題由M. J等[6]提出后，REN等[7]做了大量的研究工作，不但給出了一階、二階系統的包容控制的數學描述，還分別研究了固定拓撲和動態拓撲的包容控制，非線性系統的包容控制問題，有限時間的包容控制問題的研究也取得了若干成果。另外對Lagrangian系統的包容控制研究和輸出包容控制[8]的研究也開始起步。由于系統中智能體接收信息必然存在時間延遲(無通訊延遲的系統是理想化的系統模型)，因此對時間延遲系統的研究具有很重要的實際意義，Reza Olfati-Saber等[9]研究了一階連續時延系統，給出了保證系統收斂的時間延遲的界，Yu等[10]研究了二階系統中的時間延遲問題，Yang等[11]研究了離散時間系統的時間延遲問題，也有研究分別考慮輸入時延和通訊時延的系統和更為復雜的時變時延情況，Xia等[12-14]研究時間延遲問題在疾病傳播中影響感染閾值從而促使疾病爆發等實際應用領域的工作。大量的研究工作對固定時延和可變時延的情況都進行了穩定性分析研究。

時延的不可避免性和包容控制問題的重要應用激發了對具有時間延遲的多智能體系統的包容控制問題的研究，目前對時延多智能體系統的包容控制的研究較少，Liu等[15]研究二階連續系統中存在時變時延的情況，用LMI形式給出了系統實現包容控制時延需要滿足的條件，形式比較復雜，且為充分條件。本文研究時延系統的包容控制問題，研究的對象是基于有向固定拓撲的多靜態領導者的多智能體系統，假設系統中智能體之間信息傳遞存在通信時延且時延固定的情況下，應用拉普拉斯變換技術分別研究一階和二階連續時間多智能體系統，通過求取跟隨者狀態收斂的限制條件，然后應用終值定理得到跟隨者狀態的極限值。從而得到了保證系統實現包容控制的時延的限制條件，本文給出的兩個條件均為充分必要條件，形式也相對比較簡單。

1預備知識

假設1[16]在一個多智能體系統中，對每個跟隨者，都至少有一個領導者，有一條有向路徑指向它。

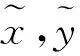
定義2[18]Laplacian矩陣L=[lij]∈Rn×n定義為

假設一個多智能體系統中有m(m

其中L1∈R(n-m)×(n-m)，L2∈R(n-m)×m關于L1和L2，有引理1和2。

引理2[20](終值定理)若函數f(t)及其一階導數都是可拉氏變換的，則函數f(t)的終值為

根據文獻[16]中的分析，可以發現，滿足假設1的系統和具有生成樹的對應系統(將系統中所有的領導者合并為一個節點)相比較，前者的Laplacian矩陣中的子矩陣L1和后者的Laplacian矩陣相比，前者的特征值比后者只是少一個0，其它特征值相同。

2主要結果

2.1一階連續系統的包容控制

多靜態領導者的一階連續多智能體系統的狀態方程為

(2)其中，aij為系統對應的鄰接矩陣的元素。矩陣L是該網絡拓撲結構對應的Laplacian矩陣，令XL(t)=[x1(t)Tx2(t)T…xm(t)T]T，XF(t)=[xm+1(t)Txm+2(t)T…xn(t)T]T(假設系統共有n個智能體，編號1到m為領導者，m+1到n為跟隨者)。τ為信息從一個節點傳送到另一個節點所需要的時間。如同時考慮狀態x為p維矢量，則跟隨者的狀態方程可寫為

(3)

定理1對一個具有相同通訊時延τ>0的多智能體系統(1)，假設通訊拓撲滿足假設1,且跟隨者之間的通訊是雙向的。若該系統使用控制協議(2)，那么該系統要取得全局漸近包容控制，當且僅當滿足條件(4)：

(4)

證明：對式(3)做Laplace變換(這里用XF(s)表示XF(t)的Laplace變換)，并整理：

(5)

(6)

要使式(3)系統中跟隨者狀態收斂，需保證系統的特征方程Zτ(s)=det(sIn-m+e-τsL1)的根具有負實部，根據文獻[9]的研究結果，滿足式(4)是系統收斂的充要條件。跟隨者狀態收斂也就是說是跟隨者的狀態是有極限的，可以對其應用終值定理，則有：

(7)

2.2二階連續系統包容控制

對多靜態領導者的二階連續系統，狀態方程如式(8)

(8)

這里xi和vi分別是第i個智能體的位置和速度。另為簡便起見，這里假定系統的位置和速度為標量(矢量的情況類似)。假設通訊時延是固定的，本文使用控制協議(9)：

(9)

其中，式(9)中的參數α>0，β>0要滿足的條件可以參考文獻[10]。

令X(t)=[x1(t)x2(t)…xn(t)]T，V(t)=[v1(t)v2(t)…vn(t)]T。

將式(9)代入式(8)也可以寫成如式(10)的簡潔形式。

(10)

對領導者和跟隨者系統，跟隨者的狀態方程為(XF，XL定義同2.1部分，VF，VL與之類似)：

(11)

則跟隨者狀態方程可簡化寫為

(12)

對系統(12)的特征方程det(λI2(n-m)-Α-e-λτB1)=0帶入矩陣A和B1并整理得：

引理3[10]假設系統的通訊拓撲網絡具有有向生成樹，則g(λ)=0有一個純虛根，當且僅當

其中，0≤θi1<2π且滿足：

其中，lm()表示虛部，Re()表示實部，ui為矩陣L1的特征值，wi1定義為

當(τ1,τ2,…,τm)變化時，當且僅當一個零點出現在或穿過虛軸，多項式P的在開放的右半平面的零點的階和才能改變。

引理5[10]假設系統的通訊拓撲網絡具有有向生成樹，λ是方程gi(λ)=0的解，則dλ/dτ在點τ∈Ψ處存在并且滿足：

定理2對一個具有相同通訊時延τ>0的多智能體二階系統(8)，假設通訊拓撲是固定的而且滿足假設1。若該系統使用控制協議(9)，那么該系統要取得全局漸近包容控制，當且僅當滿足如式(13)的條件：

(13)

證明：對式(12)做Laplace變換(這里用YF(s)表示YF(t)的Laplace變換)，并整理：

(14)

(15)

當系統的網絡拓撲是固定的且滿足假設1，可選擇參數α，β，使τ=0時，系統(12)的特征方程的根均具有負實部(因L1無0特征值，因此特征方程無0根)。根據引理3，當τ從0變化到τ0時，一個純虛根出現。根據引理4和引理5可知，當0≤τ<τ0時，特征根全部具有負實部；而當τ≥τ0時，至少有一個特征根有正實部，二階系統不收斂。從而證明條件(13)是系統(12)收斂的充分必要條件。

即時間延遲τ滿足式(13)，則系統(12)收斂，跟隨者狀態有極限值，可對其應用終值定理：

(16)

將式(16)展開可得：

(17)

此處為靜態領導者，VL(t)=0。

3仿真實例

本文采用的網絡拓撲如圖1所示，假設個體之間連接權值為1，互連個體之間通信時延為τ。

3.1一階系統實例

對一個由式(1)描述的一階連續系統，其網絡拓撲如圖1a所示，在控制協議(2)的作用下，使用式(4)計算可得，τ*=0.392 7。時間延遲τ分別取0.35和0.40的跟隨者和領導者的時間軌跡仿真圖分別如圖2a和圖2b。可以看出當τ<τ*時，跟隨者的狀態漸近收斂到領導者所組成的凸包中，而當τ≥τ*時，跟隨者的狀態發散，與定理1的結論相符。

3.2二階系統實例

對一個由式(8)描述的二階連續系統，其網絡拓撲如圖1b所示，在控制協議(9)的作用下(取α=10，β=8)，使用式(13)計算可得τ0=0.057 9。時間延遲τ取0.055的跟隨者和領導者的位置和速度時間軌跡仿真圖分別如圖3a和圖3b。可以看出當τ<τ0時，跟隨者的位置狀態漸近收斂到領導者所組成的凸包中，跟隨者的速度狀態收斂到0，與定理2的結論相符。

4結論

本文研究了具有固定通訊時延的多智能體系統的包容控制問題，假設網絡拓撲是固定有向的，系統是領導者-跟隨者結構的，多個領導者是靜態的。給出了一階、二階連續時間系統實現包容控制的時間延遲的限制條件并仿真驗證了其有效性。下一階段的任務是研究離散系統和多動態領導者情況下的時間延遲系統的包容控制問題和考慮輸入時延等情況的包容控制問題。

參考文獻:

[1]Reynolds C W.Flocks,herds and schools a distributed behavioral model[J].Computer Graphics,1987,21(4):25-34.

[2]Vicsek T, Czirok A, Ben Jacob E, et al. Novel type ofphase transition in a system of self-driven particles[J].Physical Review Letters,1995,75(6):1226-1229.

[3]Jadbabaie A, Lin J, Morse A S. Coordination of groupsof mobile agents using nearest neighbor rules[J]. IEEETranson Automatic Control,2003,48(6):988-1001.

[4]Moreau L.Stability of multi-agent systems with timedependent communication links[J].IEEE Trans onAutomatic Control,2005,50(2):169-182.

[5]Ren W, Beard R W.Consensus seeking in multi-agentsystems under dynamically changing interactiontopologies[J].IEEE Trans on Automatic Control,2005,50(5):655-661.

[6]JiM,Ferrari-Trecate G, Egerstedt M, et al. Containment control in mobile networks[J]. IEEE Transactions onAutomatic Control,2008,53(8):1972-1975.

[7]于鏑,白麗娟,李鋮.非線性多智能體網絡的分布式包容控制[J]. 復雜系統與復雜性科學,2013,10(2):63-68.

Yu Di, Bai LiJuan, Li Cheng. Distributed containment control of nonlinear multi-agent networks[J]. Complex Systems and Complexity Science,2013,10(2):63-68.

[8]Dong X W,Meng F L,Shi Z Y,et al. Output containment control for swarm systems with general lineardynamics: a dynamic output feedback approach[J].Systems & Control Letters,2014(71):31-37.

[9] Olfati-Saber R, Murray R M. Consensus problems in networks of agents with switching topology and time-delays[J]. IEEE Transaction on Automatic Control,2004,49(9):1520-1533.

[10] Yu W W,Chen G R,Cao M. Some necessary and sufficient conditions for second-order consensus inmulti-agent dynamical systems[J]. Automatica,2010,46(6):1089-1095.

[11] 楊洪勇,張嗣瀛. 離散時間系統的多智能體的一致性[J].控制與決策,2009,24(3):413-416.

Yang Hongyong, Zhang SiYing.Consensus of multi-agent system with discrete-time[J].Control and Decision, 2009,24(3):413-416.

[12] Xia C Y, Wang Z, Sanz J, et al.Effects of delayed recovery and nonuniform transmission on the spreading of diseases in complex networks[J].Physica A, 2013(392): 1577-1585.

[13] Wang L, Sun S W, Xia C Y. Finite-time stability of multi-agent system in disturbed environment[J]. Nonlinear Dynamics,2012,(67):2009-2016.

[14] Xia C Y, Wang L, Sun S W,et al.An SIR model with infection delay and propagation vector in complex networks[J].Nonlinear Dynamics,2012(69): 927-934.

[15] Liu K E, Xie G M, Wang L.Containment control for second-order multi-agent systems withtime-varying delays[J].Systems & Control Letters,2014(67):24-31.

[16] Cao Y C,Ren W,Egerstedt M.Distributed containment control with multiple stationary or dynamic leaders infixed and switching directed networks[J]. Automatica, 2012, 48(8): 1586-1597.

[17] Rockafellar R T. Convex Analysis[M]. New Jersey:Princeton University Press,1972.

[18] Ren W, Cao Y C.Distributed Coordination of Multi-agent Networks[M].London:Springer, 2011.

[19] Liu H, Xie G M, Wang L. Necessary and sufficient conditions for containmentcontrol of networked multi-agent systems[J]. Automatica,2012,48(7):1415-1422.

[20] 胡壽松.自動控制原理[M].5版.北京:科學出版社,2006:636-637.

(責任編輯耿金花)

Containment Control for Multi-Agent System with Multiple Stationary Leaders and Time-Delays

LI Bo,CHEN Zengqiang1,2, LIU Zhongxin1, ZHANG Qing2

(1. College of Computer & Control Engineering, Nankai University, Tianjin 300071， China；2.College of Science, Civil Aviation University of China, Tianjin 300300, China )

Abstract：This paper is concerned with distributed containment control of multi-agent system with multiple stationary leaders under fixed directed network topologies. Under the assumption that communication time-delays in all channels are equal, the Laplace transform is used to study the first-order and second-order multi-agent delayed system with continuous-time. Some sufficient conditions are obtained to ensure the containment of the multi-agent system by stability analysis for transfer function to get conditions and applying final value theorem. Finally,computer simulations show the effectiveness of the conclusion.

Key words:multi-agent systems; containment control; multiple stationary leaders; communication time-delays; final value theorem

文章編號：1672—3813(2016)02—0105—06;

DOI:10.13306/j.1672-3813.2016.02.013

收稿日期：2014-11-20；修回日期：2015-01-12

項目基金：國家自然科學基金(61174094)；天津自然科學基金(14JCYBJC18700，13JCYBJC17400)

作者簡介：李勃(1972-)，男，山東龍口人，博士研究生，主要研究方向為多智能體系統的包容控制。

中圖分類號:TP273

文獻標識碼:A