高速公路交通事故持續(xù)時間概率預測模型

夏正豐

（東南大學建筑設計研究院有限公司，江蘇南京 210096）

?

高速公路交通事故持續(xù)時間概率預測模型

夏正豐

（東南大學建筑設計研究院有限公司，江蘇南京 210096）

摘要：通過對寧通（南京—南通）高速公路事件數(shù)據(jù)的轉換處理，對交通事故事件展開統(tǒng)計分析，得到交通事故持續(xù)時間均值等主要信息；針對不同數(shù)據(jù)，應用不同分布模型進行擬合，發(fā)現(xiàn)事件持續(xù)時間數(shù)據(jù)分布具有右偏、長尾的特征，交通事故數(shù)據(jù)服從對數(shù)正態(tài)分布、對數(shù)Logistic分布；應用多元回歸方法建立以事件持續(xù)時間為因變量、各影響因素為自變量的多元回歸方程，對回歸方程進行影響分析，剔除異常數(shù)據(jù)，提高模型預測精度。

關鍵詞：交通安全；高速公路；事件持續(xù)時間；分布分析；逐步回歸

由于各國公路管理方式及經營理念不同，道路交通事件的分類國內外并沒有統(tǒng)一的標準。根據(jù)管理流程及工作人員的工作方式，可將高速公路事件劃分為六類，分別為交通事故類、車輛救助、其他突發(fā)事件、惡劣天氣事件、道路施工和交通管制。在上述六類事件中，交通事故和車輛救助為典型的影響高速公路運營效率和安全的事件，對其持續(xù)時間進行分析具有實際應用價值。該文以寧通（南京—南通）高速公路事件管理數(shù)據(jù)為研究對象，選擇交通事故類事件展開分析研究。

1　分布分析

采用寧通高速公路2004—2009年的205項交通事故數(shù)據(jù)，應用Minitab統(tǒng)計軟件對持續(xù)時間進行分布分析。分別選取常用的正態(tài)分布、對數(shù)正態(tài)分布、Logistic分布、對數(shù)Logistic分布、Gamma分布、Weibull分布進行擬合，同時對各分布分析進行Anderson-Darling檢驗，得到各自的AD統(tǒng)計量（見表1）。限于篇幅，這里僅提供部分回歸概率分布圖（見圖1～4）。

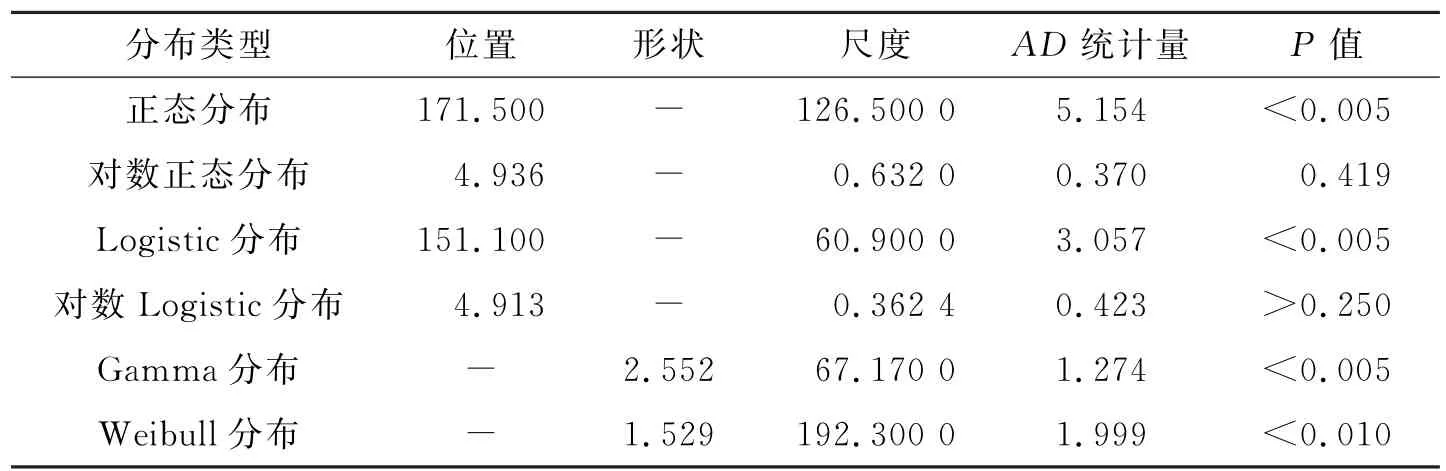
表1　交通事故的持續(xù)時間分布

圖1　交通事故持續(xù)時間的正態(tài)分布概率圖

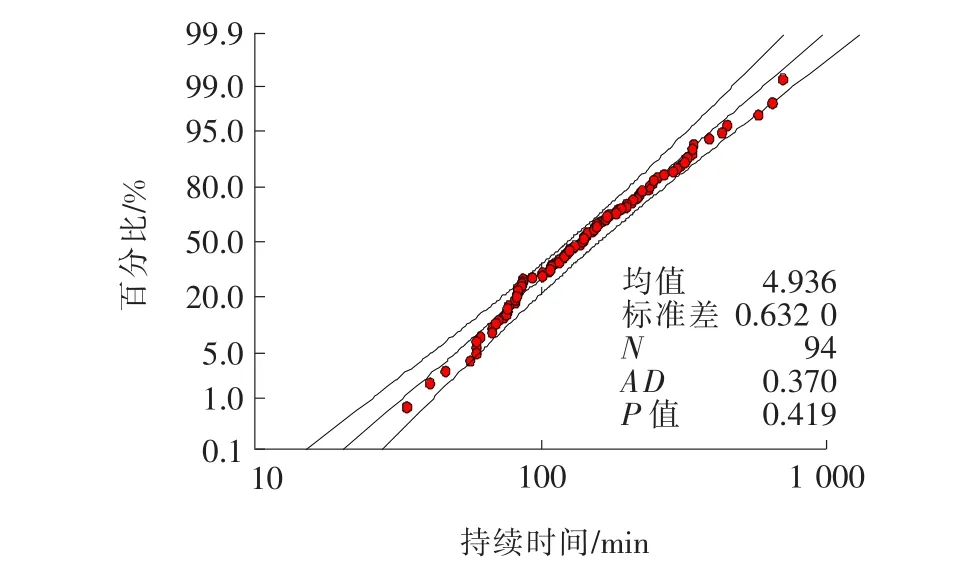
圖2　交通事故持續(xù)時間的對數(shù)正態(tài)分布概率圖

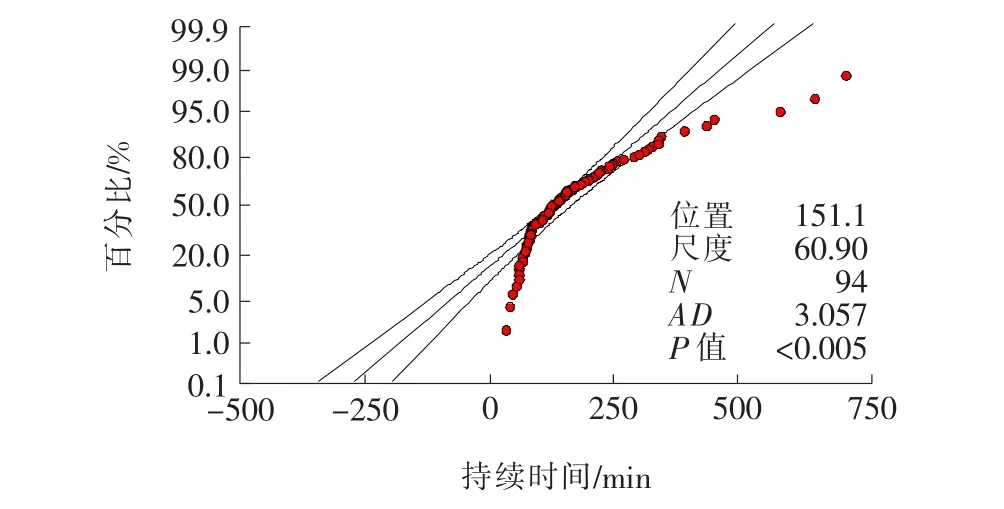
圖3　交通事故持續(xù)時間的Logistic分布概率圖

圖4　交通事故持續(xù)時間的對數(shù)Logistic分布概率圖

通過回歸分析可知：1）交通事件持續(xù)時間均值為171.5 min，標準差為124 min，中位數(shù)為110 min，最小值為33 min，最大值為713 min。對應具體原始事件信息，得知最長時間的事件發(fā)生在霧天，造成擁堵并且涉及3輛車以上；而最小時間的事件發(fā)生在晴天，只涉及1輛小車。由此可見，車輛類型、車輛數(shù)、天氣狀況、擁堵情況與持續(xù)時間的長短存在一定的內在聯(lián)系。2）如圖1～4所示，直線下半部分的曲線點表示左尾的數(shù)據(jù)比擬合分布預期的少。3）若AD檢驗的P值（如果可用）低于選定的顯著水平（0.05），則可得出數(shù)據(jù)不服從指定分布的結論。在95%置信水平下，對數(shù)正態(tài)分布和對數(shù)Logistic分布的P值大于指定的顯著水平0.05（見表1），接受原假設，可認為寧通高速公路的交通事故數(shù)據(jù)服從這兩種指定的分布，可用其進行持續(xù)時間范圍及其概率預測，而其余分布模型不能很好地表征數(shù)據(jù)分布。

2　事件持續(xù)時間線性回歸模型分析

分布分析方法和回歸分析容易理解且易于快速獲得相應的預測值，故利用類似回歸分析的數(shù)學方法建立事件持續(xù)時間模型。

在回歸分析中，因變量是事件持續(xù)時間，自變量是相關因素，主要包括時間因素、條件因素等（見表2），具體轉化過程見文獻［7］。

表2　事件持續(xù)時間相關變量的轉化

續(xù)表2

由于涉及的變量較多，采用逐步回歸的分析方法，這樣所得到的最優(yōu)方程能在最少的自變量與最佳的擬合效果之間達到平衡。所得回歸方程為：

調整的相關系數(shù)R2為0.76，F(xiàn)檢驗的統(tǒng)計量為9.62，對應的P值為零，遠小于顯著水平0.05，所以該回歸方程總體顯著。

由式（1）可知持續(xù)時間最小值為49.06 min，這對時間較短的事件預測精度不是很高，同時天氣及擁堵情況在該方程中系數(shù)較大，說明其對事件持續(xù)時間的影響顯著。此外，在20多項影響因素中只有3個顯著的變量，表明事故持續(xù)時間隨機性強，規(guī)律不明確，很難用明確的變量來區(qū)分。這3個因素在事件初期較易獲得，通過該回歸方程能提供事件發(fā)生的短期預測值，可為管理人員在第一時間發(fā)布出行信息提供幫助。

3　影響分析及模型校正

回歸分析中的一個重要假設是使用的模型對所有數(shù)據(jù)都是合適的。但實際中有可能模型適合于大多數(shù)數(shù)據(jù)，而一個或多個樣本觀測值與模型不相符。影響分析的目的是探查對擬合有異常大影響的數(shù)據(jù)并將其刪除。采用該手段，利用剩余數(shù)據(jù)通過逐步回歸方法重新建立回歸模型：

調整的相關系數(shù)R2為0.82，明顯大于式（1），F(xiàn)檢驗的統(tǒng)計量為13.71，對應的P值為零，遠小于顯著水平0.05，所得回歸方程總體顯著。比較式（1）和式（2），天氣和擁堵情況變量的系數(shù)變化較大，這也表明影響分析的必要性和有效性。利用式（2）進行預測，模型預測結果和實際值的比較見圖5。

從圖5可看出：預測值的趨勢與實際數(shù)據(jù)相符，但對于較小的實際值其預測值往往偏大、而較大的實際值其預測值往往偏小，這可能與預測模型選取的變量較少有關。采用回歸手段對交通事故持續(xù)時間進行預測所獲得的值趨向于均值，并且不會隨著時間的發(fā)展而改變，使得該方法的用途受限。

圖5　持續(xù)時間預測值與實際值的比較

4　結論

該文依托寧通高速公路，收集其交通事故和交通救助數(shù)據(jù)，分析研究了高速公路交通事件持續(xù)時間預測方法及模型，建立了交通事故持續(xù)時間的概率模型。主要結論如下：

（1）事故類持續(xù)時間遠比救助類事件長；惡劣天氣造成的事件持續(xù)時間顯著長于其他天氣情況，在高速公路運營管理中應對惡劣天氣情況下車輛的行駛加強管理及引導。

（2）事件持續(xù)時間的分布具有右偏、長尾的特點；寧通高速公路的交通事故數(shù)據(jù)服從對數(shù)正態(tài)分布和對數(shù)Logistic分布。

（3）采用逐步回歸分析的方法建立以天氣、涉及車輛數(shù)、堵車車道數(shù)為自變量的多元線性回歸方程，數(shù)據(jù)擬合表明該模型預測結果接近實際數(shù)據(jù)，能起到一定的預測作用。

參考文獻：

［1］ 劉偉銘，管麗萍，尹湘源.基于多元回歸分析的事件持續(xù)時間預測［J］.公路交通科技，2005，22（11）.

［2］ Ozbay Kaan，Pushkin Kachroo.Incident management in intelligent transportation systems［M］.Artech House，1999.

［3］ Kevin W Smith，Brian L Smith.Forecasting theclearance time of freeway accidents［R］.Smart Travel Lab Report，2001.

［4］ Choi H-K.Predicting freeway traffic incident duration an expert system context using fuzzy logic［R］.University of Southern California，1996.

［5］ Lin P，Zou N，Chang G.Integration of a discrete choice model and a rule-based system for estimation of incident duration：a case study in Maryland［A］.83rd Meeting of the Transportation Research Board［C］. 2003.

［6］ Anderson T W，Darling D A.Asymptotic theory of certain“goodness-of-fit”criteria based on stochastic processes［J］.Annals of Mathematical Statistics，1952，23（2）.

［7］ 夏正豐.高速公路交通事件持續(xù)時間建模與預測［D］.南京：東南大學，2010.

［8］ 管麗萍.高速公路事件持續(xù)時間預測方法研究［D］.長沙：長沙交通學院，2003.

［9］ 彭非，王偉.生存分析［M］.北京：中國人民大學出版社，2004.

中圖分類號：U491.3

文獻標志碼：A

文章編號：1671-2668（2016）03-0052-03

收稿日期：2015-11-27