基于博弈論角度的環境污染責任保險各方利益分析

趙雅聰 趙世浩　中央財經大學保險學院

?

基于博弈論角度的環境污染責任保險各方利益分析

趙雅聰 趙世浩中央財經大學保險學院

環境污染責任保險是以企業發生污染事故對第三人造成損害依法應承擔的責任為保障范圍的保險，具有加強企業風險管理、減輕政府善后壓力、發揮保險業社會責任等作用。自2007年試點工作開展以來，多方利益博弈激烈。本文從博弈論的視角對政府、企業、保險公司三方進行分析，論證了政府在高環境風險領域實行強制環境污染責任保險，并給予一定政策性補貼的可行性與必然性，企業作為理性人積極投保環責險分散風險的經濟性，保險公司積極承保進行風險管理的社會管理性。

當前我國已經進入經濟增長由高速轉向中高速、產業由中低端邁向中高端水平的新常態，傳統產業轉型升級的步伐不斷加快，環境問題與經濟快速發展的矛盾凸顯。我國“十三五”規劃強調綠色經濟可循環經濟的發展，而環境污染責任險作為一種分散環境污染事件風險、有助于我國環境整治的險種，正在國家的政策支持當中逐步推行。但是環境污染責任險開展涉及保險公司、企業、政府等多方利益，各方利益博弈激烈，導致環境污染責任保險在推行過程中遇到了重重阻力。基于此，本文從環境污染責任險的各方利益出發，通過博弈分析，探究環境污染責任保險各方的最優選擇，推進環境污染責任保險制度的發展。

一、簡單的企業進入動態博弈模型分析

企業在選擇進入需要投保環境污染責任保險的行業時，會考慮企業自身投保后的收益與逃避投保的收益并進行對比博弈，做出利益最大化的選擇。由此，企業與保險公司雙方構成了一個動態博弈模型。

（一）模型假設

1.設局中人為企業A和保險公司B，并且局中人都是理性經濟人（追求自身利益的最大化）。

2.假設環境污染企業A選擇不進入污染行業而選擇進入無污染綠色行業所得到的收益為R3，此時保險公司的收益為0。若環境污染企業A選擇繼續進入污染行業且保險公司承保環境污染責任保險的情況下企業收益為R2（需考慮企業在支付投保的保費等成本之后的收益），保險公司承保的收益為p。若環境污染企業A選擇進入環境污染行業但與保險公司未達成保險關系時企業收益R1（需要考慮逃避投保后保費節省以及政府排污處罰費用等的權衡），保險公司B收益為0。

（二）模型分析

首先，對企業A（即需要投保環境污染責任保險進行風險分散的企業）進行決策分析。如果R3＞R1、R2，則企業A會選擇不進入該行業轉而選擇綠色行業，則對應的該博弈結束。如果R3＜R1、R2，則企業A會選擇進入該行業。進一步分析R1、R2的大小：如果R2＜R1，企業為尋求利益最大化會選擇逃避投保，即（R1，0）；如果R2＞R1，企業會自覺投保環境污染責任保險，博弈結果為（R2，p）。

（三）結論

1.強制投保環責險提高企業的進入成本，提升行業的競爭能力

通過分析可知，投保環境污染責任保險會提高企業進入該行業的成本，將促使一些競爭實力較低的企業退出該行業，同時也會提高整個行業的內部競爭能力。通過提高成本，促進該行業的產業轉型升級，促進綠色經濟的發展。

2.實行強制性的環責險，避免企業通過逃避投保獲得超額利潤

由以上分析可以看出，R1＞R2時企業會逃避投保環境污染責任保險，此時企業獲得的部分超額利潤是通過逃避投保得到的，具有相應的負的外部性效應。因此，需要通過政府監管等形式，在高環境風險領域推行強制的環境污染責任保險。

二、考慮政府監管與企業投保的博弈分析

由以上分析可知，企業通過逃避環境污染責任險投保可能會減少相應的支出而獲得相應的超額利潤，因此需要政府對環責險的強制推行進行監管，政府監管與企業投保又構成一個博弈，通過雙方的博弈會得到利益最大化的選擇。

（二）建立純策略博弈模型

（一）模型假設

1.假設在該博弈中僅涉及政府和企業兩方決策，且政府和企業雙方能夠知道對方的決策。

2.假設政府部門對企業是否投保環境污染責任保險進行強制監管,則其支付（收益）將會是Y-C,其中Y表示企業投保環境污染責任保險帶來的經濟效益與社會效益的總和。經濟效益包括保險公司在發生環境污染事件時為企業進行的經濟支付，對污染地區的損失賠付；社會效益包括社會公眾對于積極監督企業投保環境污染責任保險履行職能的正面評價以及保險公司在事故發生時對于公眾權益的保護。C表示政府在履行監督職能時的支出。該項支出可以理解為因政府組織人員進行監管的支出等。從實際出發將其分為兩種，第一種為企業投保時政府的監管支出C1，第二種為企業未進行投保時政府的監管支出C2，按實際情況進行推斷可得C2＞C1。

3.假設政府不對投保進行監管，則政府將得到支付-Y。

4.假設企業投保與否帶來的回報分為三種情況：第一種投保環境污染責任保險的企業所需的支付為R1；第二種逃避投保環境污染責任保險且政府并未嚴格監管時得到企業的收益R2；第三種為未投保環境污染責任保險但政府實行嚴格監管對其進行相應處罰的企業所需的支付R3（可能為負）。此外，如果R1＞R2，則企業會自愿投保環境污染責任保險。因此，從實際出發即得到假設R1＜R2。

5.假設政府與企業做出監管與投保決策的概率分別為p和q。

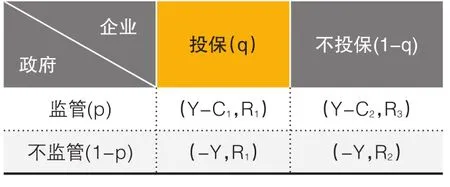
據前文的假設以及博弈矩陣,可以從以下幾種不同的情況分析納什均衡。

1.從政府監管角度分析

（1）如果Y-C1≥-Y且Y-C1≥Y-C2，即當Y≥C1/2且C1≤C2時,支付矩陣中最優結果是（Y-C1, R1）,筆者得到政府與企業博弈的一個最優決策，即納什均衡為政府傾向于嚴格監管強制高環境風險企業投保。進一步理解，政府嚴格監管強制部分企業投保的支付較高，因而可激勵其對企業進行監管。同時，考慮到政府的嚴格監管決策使企業逃避投保會受到政府的處罰，影響收益，企業也會選擇進行投保。

（2）如果Y-C2≤-Y且Y-C1≤-Y，即當Y≤C2/2時,則支付矩陣中最優結果是（-Y, R2）,筆者得到政府與企業的一個最優選擇，即對應的一個納什均衡為政府不監管且企業不投保。可以將該決策理解為，政府對企業進行環境污染責任險監管需要付出較高的成本，政府衡量支出與成本做出最優決策，即不監管；同時，企業考慮到政府不監管，也會因此而選擇不進行投保來得到最優的決策。

2.從企業投保角度分析

假設：

（1）如果企業沒有投保環境污染責任保險，企業發生意外環境污染事故造成的損失，包括對企業自身以及對企業周邊居民和員工造成的損失賠償費用、清污費用和法律費用等，將這個損失假定為R；

（2）如果企業參與了環境污染責任險，當發生環境事故時，可以將損失降低為0.3R；

（3）環境污染責任險的保費記為b；

（4）假設環境污染事件發生的概率為α。

則根據以上假設，企業投保收益為R1；

因此對于企業需要衡量-0.3Rα-b 和-Rα的大小關系，當-0.3Rα-b＞-Rα，即α＞10b/7R時，企業傾向于投保；當-0.3Rα-b＜-Rα，即α＜10b/7R時，企業不傾向于投保。企業未投保且未被監督時收益為R2；企業未投保且被監督受處罰的收益為R3，其中處罰費用為T。

根據環境污染事件發生的概率得出相應的收益函數：

（三）運用混合策略博弈模型分析

根據上文做出的對政府和企業進行選擇的概率的假設，筆者得到一個混合策略博弈分析，探究企業與政府之間的決策關系。

假設用Up表示政府所得到支付的期望函數，相對應地，Uq表示企業所得到支付的期望函數，因而：

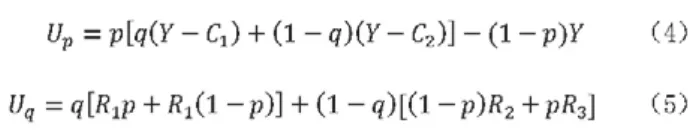
將式（4）、式（5）和式（1）、式（2）、式（3）聯立得：

分別對這兩個函數求一階偏導，求出最優條件，則有：

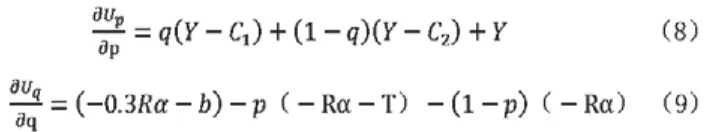
分別讓式（3）、式（4）等于0，由此，可以得到混合策略納什均衡解：

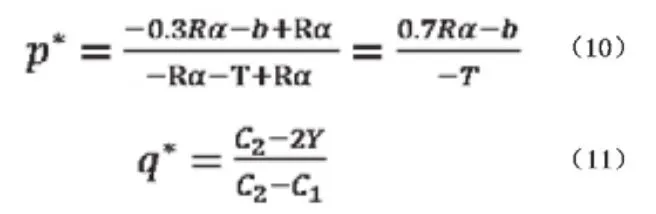
根據以上兩式可以分析R變化導致的p*、q*變化情況。

（四）結論

由以上關于p*、Rα、q*的計算，可以得知Rα、p*之間成正相關關系。也就是說，隨著Rα的減小，p*隨之減小；隨著Rα的增大，p*隨之增大。

由以上分析可知，當環境污染責任事件造成的損害越大，政府就有越大的可能性對環境污染責任險投保進行監管，對投保企業進行管理。

三、考慮事故賠付的保險公司與企業的博弈

根據以上分析可以得到政府與企業雙方博弈的最優選擇。筆者進一步引入保險公司對于環責險進行理賠的因素進行分析，考慮保險公司對于是否承保環責險的選擇。

（一）根據以上分析得出保險公司收益函數

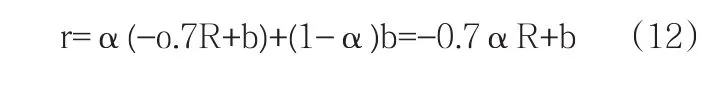
當r＞0，即α＜10b/7R時，保險公司對應地能獲得利潤而愿意承保。當r＜0，即α＞10b/7R時，保險公司承保不能獲得利潤。但是通過式（1）的分析保險公司獲利條件α＜10b/7R，與企業投保條件相互矛盾，因此，需要政府對相應的政策性保險公司提供政策補貼。

（二）加入政策補貼因素的保險公司收益函數

假設政府補貼為M，則

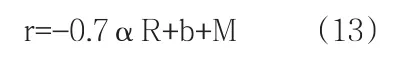
當r＞0，即α＜（10（b+M））/7R時，保險公司對應地能獲得利潤。當r＜0，即α＞（10（b+M））/ 7R時，保險公司承保不能獲得利潤。因而企業與保險公司博弈結果為10b/7R＜α＜（10（b+ M））/7R時，企業選擇投保環境污染責任保險，保險公司也愿意承保。政府應給予保險公司一定的補貼，保險公司根據補貼情況在一定環境污染事件概率內承保。

通過以上分析可以得到政府、企業、保險公司三方的最優選擇。

四、結論

（一）政府及相關環保部門應強制高環境風險企業投保環境污染責任保險。如果政府采取企業自愿投保政策，部分企業可能會逃避投保責任，在環境污染事故發生時無力承擔經濟賠償與環境恢復的社會責任，同時影響政府形象。在整個機制運行中，政府應積極承擔政策法規制定、運行機制監管、財政補貼支持等多項職能。

（二）企業應根據環境污染事件發生概率選擇是否投保環境污染責任保險。此時可引入專業第三方機構來測評企業環境事故發生概率及風險等級。當概率α＞10b/7R時，應通過環境污染責任保險來分散風險。政府也可根據企業的自身風險等級來確定強制投保企業名錄。

此外，由于環境污染事件帶來的損失額一般比較巨大，即Rα值比較大，根據式（10）的分析可以看出，政府應更傾向于對環境污染責任保險進行監管。

（三）保險公司是環境污染責任保險推廣中的重要主體，具有營利性，而環境污染責任保險本身具有公益性、社會性，需要政府給予一定的財政支持。