基于EKF的船舶模型預測動力定位導引控制器設計

劉　菊, 熊曉東, 汪大鵬, 李　鵬

(1. 哈爾濱工程大學，黑龍江 哈爾濱 150001； 2. 上海船舶工藝研究所，上海 200032；3.渤船重工船舶設計院，遼寧 葫蘆島 125000；4.金海重工股份有限公司，浙江 舟山，316291)

?

基于EKF的船舶模型預測動力定位導引控制器設計

劉菊1, 熊曉東2, 汪大鵬3, 李鵬4

(1. 哈爾濱工程大學，黑龍江 哈爾濱 150001； 2. 上海船舶工藝研究所，上海 200032；3.渤船重工船舶設計院，遼寧 葫蘆島 125000；4.金海重工股份有限公司，浙江 舟山，316291)

摘要傳統的動力定位船舶導引控制系統包括產生動態目標點的導引子系統和產生導引點跟蹤效果的控制子系統，用于較近的定位點之間的轉移過程中。傳統導引控制系統雖然已經成功地應用于動力定位控制系統中，但控制系統設計工作復雜，實際作業時不能自定義修改最大導引速度，海洋環境會對導引控制效果有所影響。本文設計了一種基于模型預測控制(MPC)的船舶動力定位導引控制系統，該控制系統不必進行導引子系統設計，可以直接處理定位點之間的導引控制，同時設計了擴展卡爾曼濾波器(EKF)為該控制器提供必要的狀態估計，并進行了仿真試驗，仿真結果驗證了濾波器和控制器的有效性。

關鍵詞模型預測控制約束控制導引控制擴展卡爾曼濾波器

0引言

隨著船舶行業的多樣化發展，船舶動力定位系統的應用越來越廣泛，船舶的動力定位是指船舶出于必要原因需要從當前定位點轉移到新的定位點。當船舶定位點間距離較遠時，可以將船舶常速行進至新定位點附近，再啟動定位導引操縱控制系統，逐漸將船舶控制到定位點。當兩定位點相距不太遠時，不必加速轉移船舶，直接啟動特定的導引操縱控制系統來引導船舶到達指定定位點。

導引操縱控制系統屬于實際工程應用功能系統，實際作業時一般是根據預定義的導引速度從當前定位點產生一系列到達目標定位點的動態路徑點，然后針對不同的預定導引速度設計控制器實現對動態目標點的跟蹤，直至將船舶導引到目標定位點。傳統的導引操縱控制系統一般包括制導子系統和控制子系統，如圖1所示。導引控制子系統是基于PID控制方法，針對不同的預定導引速度設計各自的PID控制器，制導子系統在線產生一系列導引路徑點作為控制系統的動態目標點。

圖1　傳統動力定位導引控制系統方框圖

本文提出一種簡潔的新型導引操縱控制方法——基于模型預測控制(MPC)的導引操縱控制，它能夠實現從當前定位點低速運動至目標點附近，而無需傳統的制導子系統。具體步驟如下：首先建立仿真和控制用的船舶數學模型，并進行擴展卡爾曼濾波器設計，然后進行模型預測控制器設計，之后設計了仿真試驗對濾波器和控制器進行驗證分析，最后給出了論文結論。

1船舶運動數學模型建立[1]

1.1參考坐標系

船舶運動數學模型分為兩類：仿真模型和控制模型。仿真模型主要起到代替實船的作用，產生船舶運動狀態信息；控制模型一般較仿真模型簡單，用于控制器和觀測器的分析和綜合。不管是哪類模型，建模的時候都要首先確立船舶運動的參考系統。描述船舶運動數學模型時一般采用兩種右手坐標系統：慣性坐標系統OXEYEZE(NED坐標系)和附體坐標系統OXYZ，如圖2所示。其中，NED坐標系為固定于地球表面的慣性坐標系統，取作基準參考系統，規定XE軸指向正北方向，YE軸指向正東方向，ZE軸指向地心方向；附體坐標系OXYZ是原點位于船舶中某指定點O(對于水面船舶通常取作滿載吃水平面的前后左右中心點)上的非慣性坐標系。

圖2　船舶運動參考坐標系和運動變量

1.2仿真模型[2]

1.2.1裸船體模型

在船舶動力定位領域，關注重點是艏向角ψ和位置信息n和e的變化，即船舶在水平面內的運動。船舶水平面運動數學模型為

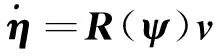
(1)

(2)

式中：η=[neψ]T表示船舶在NED坐標系統中的位置和艏向信息；v=[uvr]T代表船舶的縱向、橫向速度和回轉角速度；R(ψ)為狀態轉換矩陣，如式(3)所示；M=MT>0為質量和慣量矩陣；C(v)為Coriolis力和向心力矩陣；D為線性阻尼矩陣；DNL(v)為非線性阻尼矩陣；τ=[τXτYτN]T代表三個自由度上的控制輸入作用；w代表環境干擾。

1.2.2環境干擾模型

環境干擾包括風浪流的低頻干擾和高頻干擾。對于低頻干擾，要對風、浪、流分別建模，不失一般性只需考慮風的影響，認為w=[XWindYWindNWind]T。作用于船體上的平均風干擾力和力矩為

(3)

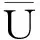
海洋環境的高頻干擾以高頻運動分量的形式疊加到低頻運動分量上。波頻模型如下:

(4)

式中：ξ∈R6×1為高頻分量的狀態向量；Aw∈R6×6為與海洋環境相關的矩陣；Ew∈R6×3、Cw∈R3×6為定值矩陣。

1.2.3測量模型

系統的測量模型為

(5)

式中：v為測量白噪聲。

1.3控制模型[3]

控制器和觀測器分析和綜合是需要用到控制模型。控制模型如下:

(6)

式中：b∈R3為緩慢變化的環境低頻干擾。

2擴展卡爾曼濾波器(EKF)

2.1基于狀態估計的濾波模型

(7)

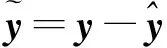
2.2擴展卡爾曼算法

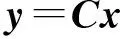
(8)

式中：C=[CwI3×303×303×3]；

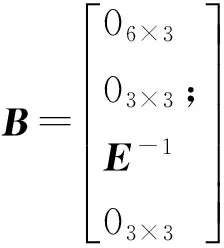
動力定位船舶在進行導引操縱時，其航向ψ變化較小，在ψ附近對模型進行線性化

(9)

(10)

式中：Fk=I-TsA；Δ=TsB；Γ=TsE，其中Ts為仿真步長；下標k表示第k仿真時刻。

EKF算法如下：

狀態預測

(11)

協方差預測

(12)

殘差

(13)

殘差協方差

(14)

次優卡爾曼增益

(15)

狀態估計

(16)

協方差估計

(17)

濾波步驟如下。

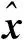
(2) 執行上述EKF算法。

(3) 如不滿足結束條件，k+1。

(4) 進入步驟(1)。

3基于模型預測控制的定位導引操縱控制器[4]

模型預測控制在工業界和學術界都得到了持續的關注。其本身固有的優化功能和魯棒性使其在船舶運動控制領域具有良好的發展前景。

模型預測控制系統的設計是基于系統狀態空間數學模型的。假定控制系統的狀態信息為xm=[ηTvTbT]T，在進行狀態的向前預測時所需要的當前狀態信息xm(k)是觀測器傳遞過來的當前估計信息。假設采用周期為Ts，將低頻控制模型的微分代數方程(11)～(13)進行一階前向歐拉離散得到差分代數方程，作為控制器的預測模型。如果以x+表示下一時刻的狀態信息，則有

(18)

(19)

式中：下標m代表與船舶模型相關；

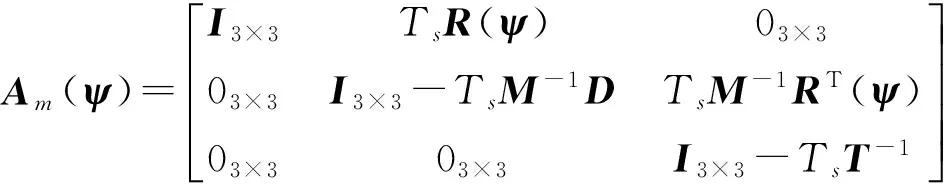
對于預測時域為Np的滾動時域控制，由于船舶的慣性大，因此滾動時域內可認為Am(ψ)可以在滾動時域初始時刻的艏向ψ0附近進行線性化得到Am。得到線性離散狀態空間方程:

(20)

式中：k=0,1,…,Np-1代表預測步數，其中N為預測時域長度。為方便構建預測模型，定義以下變量:

(21)

(22)

選取x(k)=[Δxm(k)Ty(k)T]T作為預測控制系統的新狀態。原船舶模型等價轉化為以下擴展模型。

(23)

(24)

不失一般性以后均以下標代表預測步數；

3.1預測模型

根據狀態空間模型(A，B，C)，狀態預測如下:

同理得到輸出預測模型

(25)

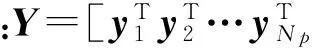
F=[(CA)T(CA2)T(CA3)T…(CANp)T]T。

3.2預測控制

假定期望輸出為yd，選取代價函數如下。

(26)

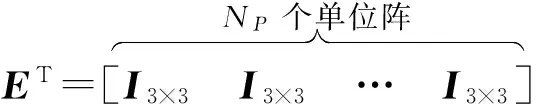
(27)

對應的最優控制序列滿足以下條件。

對應的最優控制序列為

(28)

以上為系統無約束時的預測控制最優解，鑒于實際系統的約束，需要滿足狀態軟約束xmin≤xk≤xmax和輸入硬約束Δumin≤Δuk≤Δumax、umin≤uk≤umax。為方便優化，將約束條件寫成如下形式。

(29)

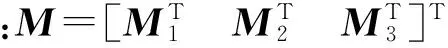
控制幅度約束：

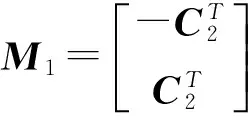
控制增量約束：

狀態約束：

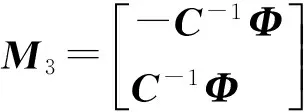
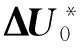
(30)

4仿真試驗

四級海情下，船舶受海洋環境干擾無動力自由漂浮，仿真軌跡和估計軌跡如圖3所示，各狀態估計和仿真對比如圖4～圖6所示。由圖示可知，濾波器成功地濾去了船舶運動的高頻分量，估計值與仿真或者測量值接近。

圖3　估計軌跡和測量軌跡的對比

圖4　位置估計值和測量值對比

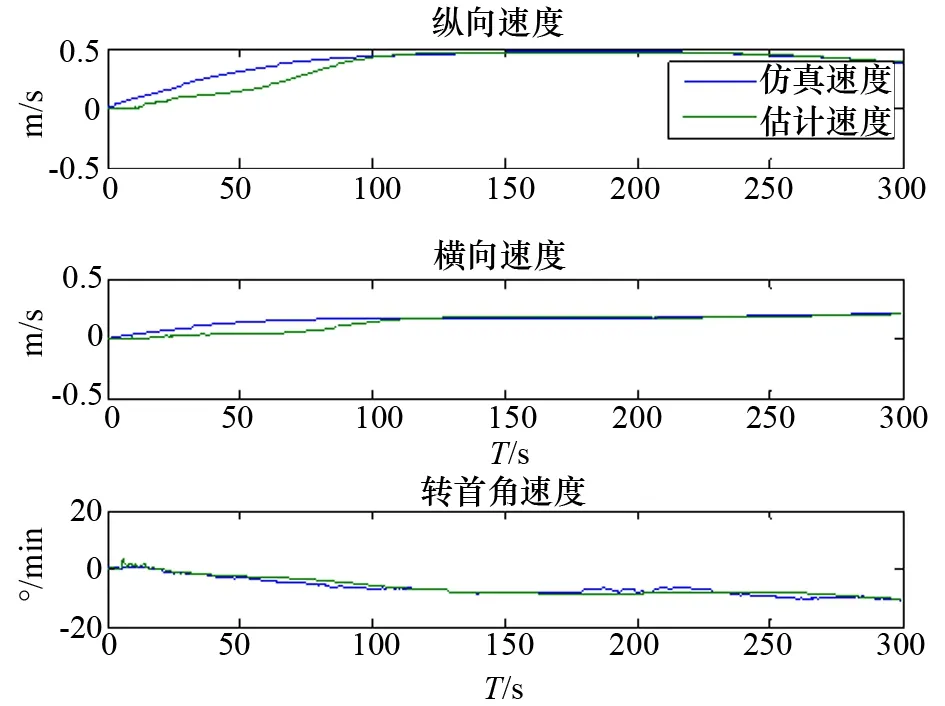
圖5　速度的估計值和仿真值對比

圖6　環境干擾的估計值和仿真值對比

船舶初始位置和艏向為yinit=[0 m 0 m 10°]T，期望位置為yd=[20 m 15 m 10°]T。控制器參數如下：預測時域NP=50，控制時域NC=5，輸出輸入權值矩陣Q=diag(103,103，106)、R=diag(10-6,10-6,10-8)。圖7為導引過程船舶運動軌跡圖，導引過程中的狀態信息如圖7～圖9所示。

圖7　導引過程中的船舶軌跡

圖8　導引過程中的位置和艏向

5結論

根據仿真結果可以看到，濾波器成功地濾去了船舶運動的高頻分量，濾波效果能夠滿足控制系統的需要，同時卡爾曼濾波器(EKF)的模型預測控制系統能夠有效地進行定位點之間的導引操縱。

6結束語

圖9　導引過程中的速度信息

船舶動力控制系統中傳統的PID控制器由于局部有效性和較差的魯棒性限制了其遠距離定位的控制效果，為保證控制效果必須設計導引系統，逐步產生動態新目標點，逐步地引導船舶到達最終目標點，增加了控制系統的復雜度。基于卡爾曼濾波器(EKF)的模型預測控制固有的優化功能和魯棒性使其可以實現并且簡化導引操縱過程，其優勢如下。

(1) 結構更簡潔。整個控制系統不再需要制導系統，制導算法設計及實現不再必要。

(2) 使用更方便。控制器參數調試更簡單，不同海洋環境下也能低速運動至目標點附近，而不必重新設計不同的控制器參數。

(3) 更高的經濟性。MPC本質上是一種最優控制方法，產生的控制輸入是某種形式上的最優控制，能夠減少船舶動力控制能耗和控制器磨損。

參考文獻

[1]賈欣樂,楊鹽生.船舶運動數學模型[M].大連：大連海事大學出版社,1998.

[2]Konsberg. Operator Manual: Kongsberg K-Pos DP-2[M].Konsberg Maritime AS， 2006.

[3]Wang L. Model Predictive Control System Design and Implementation Using MATLAB[J]. Springer Berlin, 2009, 39(12):110-114.

[4]Thor I， Fossen. Marine Control Systems: Guidance, Navigation and Control of Ships, Rigs and Underwater Vehicles[M]. Marine Cybernetics,2002.

EKF Based Model Predictive Controller Design for Dynamic Positioning Ship Guidance Control

LIU Ju1， XIONG Xiao-dong2， WANG Da-peng3， LI Peng4

(1. Harbin Engineering University, Harbin Heilongjiang 150001, China;2.Shanghai Shipbuilding Technology Research Institute, Shanghai 200032, China;3. Bohai Shipbuilding Heavy Industry Co., Ltd., Huludao Liaoning 125000, China;4.Jinhai Heavy Industry Co., Ltd., Zhoushan Zhejiang 316291, China)

AbstractTraditional guidance control system of dynamic positioning ship includes a guidance subsystem generating path points toward target dynamic positioning point and a control subsystem performing path-point tracking during the transfer process between the current and next dynamic positioning points. The conventional guidance control system has been successfully applied to dynamic positioning control system, but the control system is complicated to design and tune in varying sea. This paper presented a Model Predictive Control (MPC) based guidance controller for the dynamic positioning ship while not necessary to design the guidance subsystem, directly controlling the dynamic positioning ship toward the range of the target point. Meanwhile an Extended Kalman Filter (EKF) was designed to provide the necessary state estimation for the controller. Simulation experiments were carried out to verify the efficiency of the filter and the controller. The simulation results demonstrate the efficiency of the presented filter and controller.

KeywordsModel predictive controlConstrained controlGuidance controlExtended Kalman Filter(EKF)

中圖分類號U662

文獻標志碼A

作者簡介：劉菊(1986-)，女，博士研究生，研究方向為基于模型預測控制的動力定位。