具可變時滯的二階非線性中立型泛函微分方程的振動性
楊 甲 山
(梧州學院 信息與電子工程學院, 廣西 梧州 543002)
?
具可變時滯的二階非線性中立型泛函微分方程的振動性
楊 甲 山
(梧州學院 信息與電子工程學院, 廣西 梧州 543002)
摘要:研究一類非線性的具有可變時滯的二階中立型泛函微分方程的振動性,利用Riccati變換技術及不等式分析技巧,獲得了該方程振動的2個新的判別準則,所舉例子說明這些準則是方程振動的“sharp”條件.
關鍵詞:振動性;變時滯;泛函微分方程;Riccati變換
微分方程在自然科學及工程技術等領域有著非常廣泛的應用,如著名的二階Emden-Fowler型微分方程x″(t)+at-1x′(t)+btm-1xn(t)=0已廣泛應用于數學物理、理論物理(特別是核物理)、生物工程、信息技術及工程機械等領域.近年來具變時滯的中立型泛函微分方程的振動性研究引起了國內外學者的廣泛興趣[1-24].筆者考慮如下形式的具變時滯的二階非線性中立型微分方程
{a(t)[(x(t)+p(t)x(τ(t)))′]γ}′+
q(t)f(x(δ(t)))=0,t≥t0
(1)
的振動性,其中,函數a,p,q∈C([t0,+∞),R);常數γ為2個正奇數之商;函數f∈C(R,R)并且uf(u)>0(u≠0),本文假設下列條件成立:
(H1) a∈C1([t0,+∞),(0,+∞)),q(t)>0,p(t)≥0.
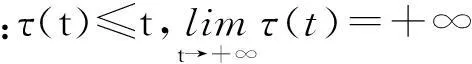
(H3)當u≠0時,f(u)/u≥L(這里常數L>0).
如果x(t)滿足a(t)[(x(t)+p(t)x(τ(t)))′]γ∈C1([Tx,+∞),R),且在區間[Tx,+∞)滿足式(1),則稱函數x(t)∈C1([Tx,+∞),R)(Tx≥t0)是方程(1)的解,本文只關注方程(1)的非平凡解.如果方程(1)的解x(t)既不最終為正也不最終為負,則稱解x(t)是振動的,否則是非振動的;如果方程(1)的所有解都是振動的,則稱其是振動的.本文將分別在條件
(2)
和
(3)
成立的情況下建立方程(1)的振動性判別準則,改善對方程(1)的中立項系數函數的限制條件:0≤p(t)<1,得到這些準則的特殊情形,推廣并改進了最近文獻中的一系列結果.
引理1設A>0,B>0和λ>0均為常數,則
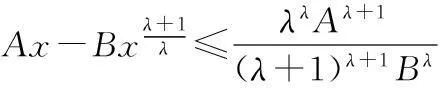
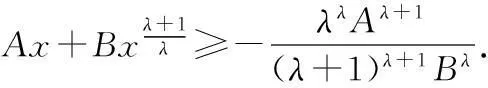
可由數學分析法證明之.
1主要結果及其證明
引入記號
z(t)=x(t)+p(t)x(τ(t)),
Q(t)=min{q(t),q(τ(t))},
φ+(t)=max{φ(t),0}.
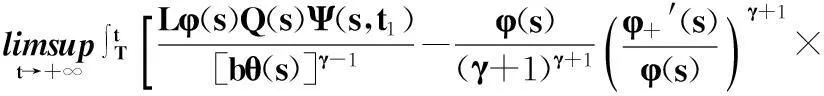
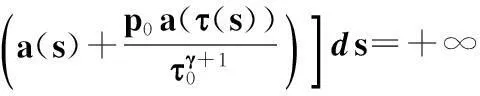
(5)
其中常數T≥t0足夠大,b>0,函數
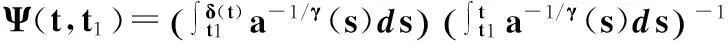

則方程(1)是振動的.
證明用反證法:設方程(1)有一個最終正解x(t)(當x(t)為最終負解時類似可證),則?t1≥t0,當t≥t1時,有x(t)>0,x(τ(t))>0,x(δ(t))>0.由z(t)的定義,有z(t)>0,z(t)≥x(t)(t≥t1).由方程(1),
[a(t)(z′(t))γ]′=-q(t)f(x(δ(t)))≤
-Lq(t)x(δ(t))<0,
(6)
由此式容易證得z′(t)>0(t≥t1).應用式(6),
當t≥t1時,有
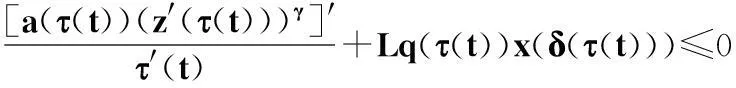
(7)
綜合式(6)與(7),當t≥t1時,得
[a(t)(z′(t))γ]′+Lq(t)x(δ(t))+
p0Lq(τ(t))x(δ(τ(t)))+
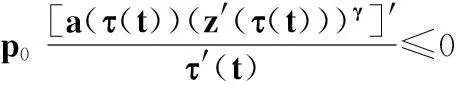
-LQ(t)[x(δ(t))+p0x(δ(τ(t)))]≤
-LQ(t)z(δ(t))≤0,
(8)
令

(9)
則w(t)>0(t≥t1),利用式(9)及引理1(i),可得

(10)
再令
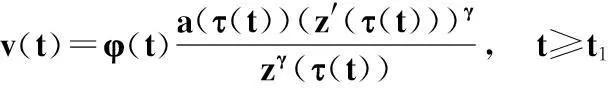
(11)
則v(t)>0(t≥t1).由于τ′(t)≥τ0>0,z′(t)>0,由引理1(i),類似地可得
(12)
于是,綜合式(10),(12),并注意到式(8),可得

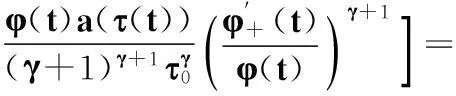
(13)
由式(6)知,a(t)[z′(t)]γ(t≥t1)是單調減少的,因此有
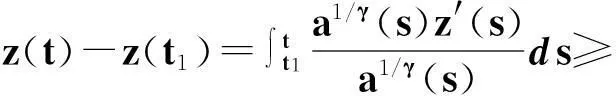
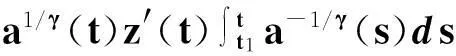
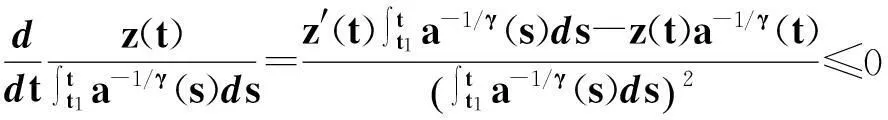
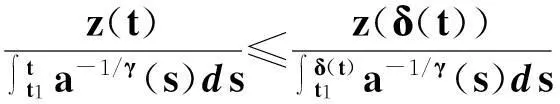
(14)
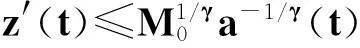

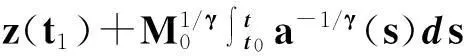
所以,存在充分大的t2≥t1及常數b>0,當t≥t2時,就有
(15)
將式(14),(15)代入式(13),得
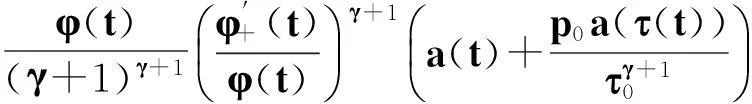
所以
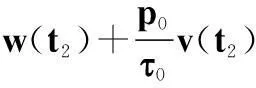
這與式(5)矛盾.定理1證畢.
定理2設式(3)成立,且0≤p(t)≤p0<+∞(p0為常數),若存在函數φ∈C1([t0,+∞),(0,+∞))使得式(5)成立,且

(16)
其中常數T≥t0足夠大,函數
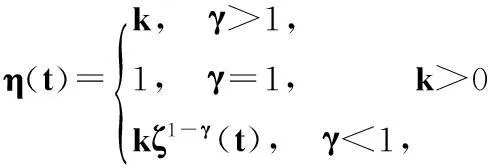
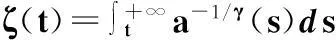
證明用反證法:設方程(1)有一個最終正解x(t)(當x(t)為最終負解時類似可證),則?t1≥t0,當t≥t1時,有x(t)>0,x(τ(t))>0,x(δ(t))>0,根據定理1的證明,a(t)[z′(t)]γ嚴格單調遞減且最終定號,進而z′(t)最終為正或為負.因此只需考慮如下2種情形:
情形iz′(t)>0(t≥t1).證明同定理1,可得到一個與式(5)矛盾的結果.
情形iiz′(t)<0(t≥t1).定義函數w(t)如下:
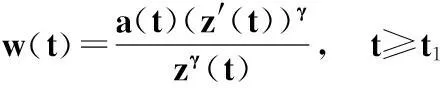
(17)
則w(t)<0(t≥t1),并且

(18)
利用a(t)[z′(t)]γ的單調遞減性,當s≥t≥t1時,有a(s)[z′(s)]γ≤a(t)[z′(t)]γ,進而
z′(s)≤a1/γ(t)z′(t)a-1/γ(s),
此式兩邊從t到u(u≥t)對s積分,可得
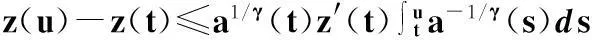
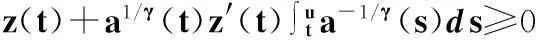
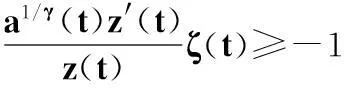
-1≤w1/γ(t)ζ(t)≤0,t≥t1.
(19)
定義函數v(t)如下:
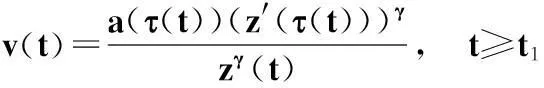
(20)
則v(t)<0(t≥t1).再利用a(t)[z′(t)]γ的單調遞減性,有
a(τ(t))[z′(τ(t))]γ≥a(t)[z′(t)]γ,
進一步,
于是,由式(20),并利用z′(t)<0,可得
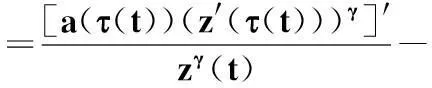
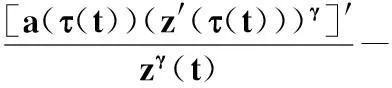
(21)
由a(τ(t))[z′(τ(t))]γ≥a(t)[z′(t)]γ,得v(t)≥w(t),利用式(19),同樣有
-1≤v1/γ(t)ζ(t)≤0,t≥t1.
(22)
由式(18)和(21),并應用式(8)(由定理1的證明知,此時式(8)仍然成立)及z(δ(t))≥z(t),可得
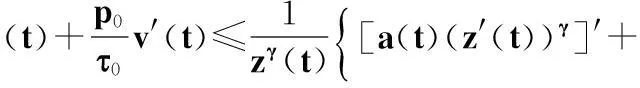
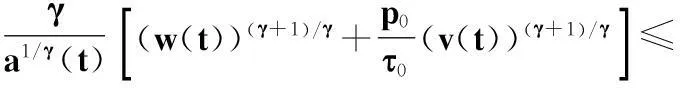

(23)
當γ>1時,因為z(t)>0,z′(t)<0(t≥t1),所以z(t)≤z(t1),即z1-γ(t)≥z1-γ(t1)=k.
當γ=1時,顯然有z1-γ(t)=1.
當γ<1時,由于a(t)[z′(t)]γ是單調減小的,所以當s≥t≥t1時,有
a(s)[z′(s)]γ≤a(t)[z′(t)]γ,
即
z′(s)≤{a(t)[z′(t)]γ}1/γa-1/γ(s),
因此
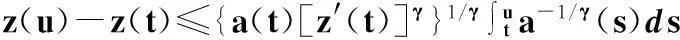
有
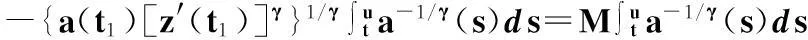
這里M=-{a(t1)[z′(t1)]γ}1/γ=-a1/γ(t1)z′(t1)>0為常數,令u→+∞,則由上式得
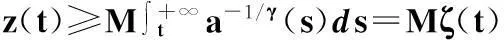
即z1-γ(t)≥M1-γζ1-γ(t).
綜合上述3種情形及函數η的定義,由式(23),得
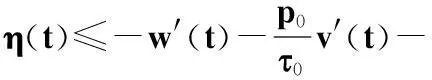
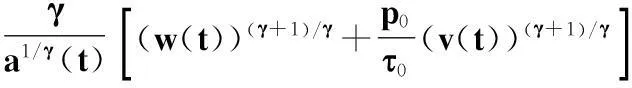
上式兩邊乘以ζγ(t)并從t1到t(t≥t1)積分,采用分部積分法,ζ′(t)=-a-1/γ(t),由式(19)和(22),以及引理1(ii),得
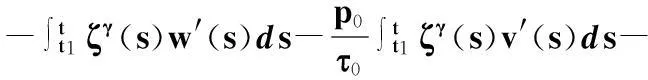
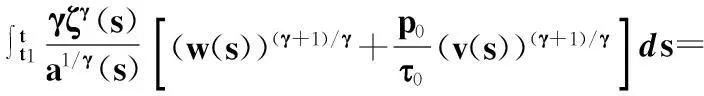
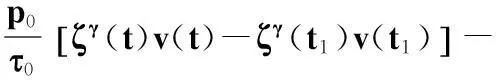
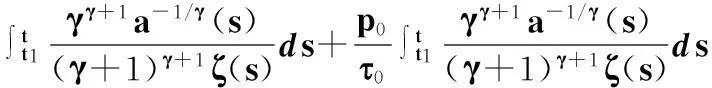
所以,
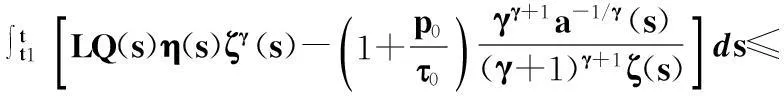
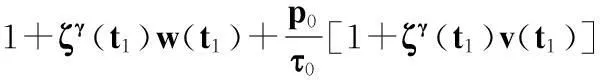
這與式(16)矛盾.定理2證畢.

2實例分析
例1考慮如下二階微分方程(α>0為常數):
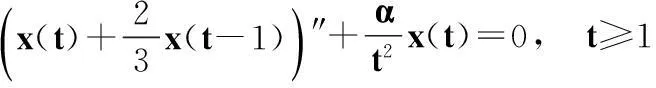
(24)
這里γ=1,a(t)≡1,p(t)=2/3,q(t)=α/t2,τ(t)=t-1,δ(t)=t,f(u)=u.容易驗證,條件(H1)~(H3)均滿足.現取φ(t)=t,注意到L=1,p0=2/3,τ0=1,Ψ(s,t1)=1,則
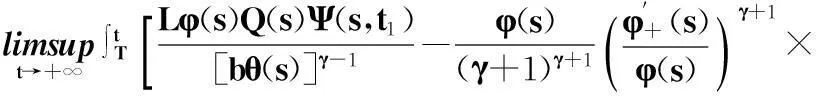
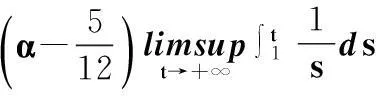
所以由定理1知,當α>5/12≈0.416 67時,方程(24)是振動的.
注2現改用文獻[12]中的定理2.1來判定:因為
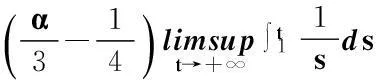
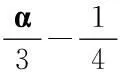
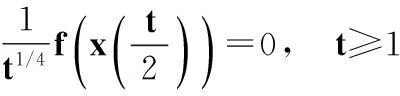
(25)
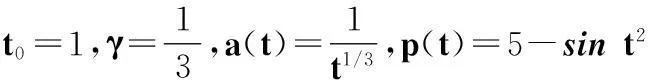
取f(u)=u[1+ln(1+u4)],因為
0 且 所以條件(H1)~(H3)全部滿足.又因為 Q(t)=min{q(t),q(τ(t))}=t-1/4, 且 為簡化計算,取φ(t)=1,T=3,則 所以定理1的條件全部滿足,于是由定理1知方程(25)是振動的. 注3筆者注意到,由于方程(25)的中立項系數函數p(t)>1,因此文獻[1-3,5-8,11-16,19-22]等中的定理對方程(25)均不適用. 參考文獻(References): [1]HASANBULLI M, ROGOVCHENKO Y V. Oscillation criteria for second order nonlinear neutral differential equations[J]. Applied Mathematics and Computation,2010,215(12):4392-4399. [2]LI Tongxing, AGARWAL R P, BOHNER M. Some oscillation results for second-order neutral differential equations[J]. The Journal of the Indian Mathematical Society,2012,79(1-4):97-106. [3]LI Tongxing, AGARWAL R P, BOHNER M. Some oscillation results for second-order neutral dynamic equations[J]. Hacettepe Journal of Mathematics and Statistics,2012,41(5):715-721. [4]LI Tongxing, ROGOVCHENKO Y V. Asymptotic behavior of higher-order quasilinear neutral differential equations[J]. Abstract and Applied Analysis,2014,doi:org/10.1155/2014/395368. [5]LI Tongxing, ROGOVCHENKO Y V, ZHANG Chenghui. Oscillation of second-order neutral differential equations[J]. Funkcialaj Ekvacioj,2013,56(1):111-120. [6]AGARWAL R P, BOHNER M, LI Tongxing, et al. Oscillation of second-order Emden-Fowler neutral delay differential equations[J]. Annali di Matematica Pura ed Applicata,2014,193(6):1861-1875. [7]ZHANG Chenghui, AGARWAL R P, BOHNER M, et al. New oscillation results for second-order neutral delay dynamic equations[J]. Advances in Difference Equations,2012,2012:227.dol:10.1186/1687-1847-2012-227. [8]AGARWAL R P, BOHNER M, LI Tongxing, et al. A new approach in the study of oscillatory behavior of even-order neutral delay differential equations[J]. Appl Math Comput, 2013,225:787-794. [9]YANG Jiashan, QIN Xuewen. Oscillation criteria for certain second-order Emden-Fowler delay functional dynamic equations with damping on time scales[J]. Advances in Difference Equations, 2015(1):1-16. [10]YANG Jiashan, QIN Xuewen, ZHANG Xiaojian. Oscillation criteria for certain second-order nonlinear neutral delay dynamic equations with damping on time scales [J]. Mathematica Applicata, 2015,28(2):439-448. [11]SUN Shurong, LI Tongxing, HAN Zhenlai, et al. On oscillation of second-order nonlinear neutral functional differential equations[J]. Bulletin of the Malaysian Mathematical Society,2013,36(3):541-554. [12]YE L, XU Z. Oscillation criteria for second order quasilinear neutral delay differential equations[J]. Applied Mathematics and Computation,2009,207(2):388-396. [13]SUN Shurong, LI Tongxing,HAN Zhenlai,et al. Oscillation theorems for second-order quasilinear neutral functional differential equations[J]. Abstract and Applied Analysis,2012,2012:1-17.dol:10.1155/2012/819342. [14]楊甲山,方彬.一類二階中立型微分方程的振動性[J].數學的實踐與認識,2013,43(23):193-197. YANG Jiashan, FANG Bin. Oscillation of a class of second order neutral differential equations[J]. Mathematics in Practice and Theory, 2013,43(23):193-197. [15]楊甲山.具阻尼項的高階中立型泛函微分方程的振蕩性[J].中山大學學報:自然科學版,2014,53(3):67-72. YANG Jiashan. Oscillation of higher order neutral functional differential equations with damping[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni,2014,53(3):67-72. [16]楊甲山.具正負系數和阻尼項的高階泛函微分方程的振動性[J].華東師范大學學報:自然科學版,2014(6):25-34. YANG Jiashan. Oscillation of higher order functional differential equations with positive and negative coefficients and damping term[J].Journal of East China Normal University: Natural Science,2014(6):25-34. [17]楊甲山,張曉建.具阻尼項的二階擬線性泛函差分方程的振蕩性判別準則[J].浙江大學學報:理學版,2015,42(3):276-281. YANG Jiashan, ZHANG Xiaojian. Oscillation criteria for a class of second order quasilinear functional difference equation with damping[J].Journal of Zhejiang University:Science Edition,2015,42(3):276-281. [18]楊甲山.時標上一類具阻尼項的二階動態方程的振蕩性[J].系統科學與數學,2014,34(6):734-751. YANG Jiashan. Oscillation for a class of second-order dynamic equations with damping on time scales[J]. Journal of Systems Science and Mathematical Sciences,2014,34(6):734-751. [19]LI Tongxing, ROGOVCHENKO Y V, TANG S. Oscillation of second-order nonlinear differential equations with damping[J]. Mathematica Slovaca,2014,64(5):1227-1236. [20]楊甲山,覃學文.具阻尼項的高階Emden-Fowler型泛函微分方程的振蕩性[J].中山大學學報:自然科學版,2015,54(4):63-68. YANG Jiashan, QIN Xuewen. Oscillation of higher order Emden-Fowler functional differential equations with damping[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni,2015,54(4):63-68. [21]楊甲山,張曉建.具正負系數的二階阻尼微分方程的振動性[J].高校應用數學學報:A輯,2011,26(4):399-406. YANG Jiashan, ZHANG Xiaojian. Oscillation of second order damped differential equation with positive and negative coefficients[J]. Applied Mathematics A Journal of Chinese Universities:Ser A,2011,26(4):399-406. [22]楊甲山.具正負系數和阻尼項的高階微分方程的振動定理[J].中山大學學報:自然科學版,2012,51(1):30-34. YANG Jiashan. Oscillation theorems of higher order differential equations with positive and negative coefficients and damping term[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni,2012,51(1):30-34. [23]楊甲山.一類二階非線性變時滯差分方程解的振動性[J].煙臺大學學報:自然科學與工程版,2012,25(2):90-94. YANG Jiashan. Oscillation of solutions for a class of second-order nonlinear variable delay difference equation[J]. Journal of Yantai University: Natural Science and Engineering Edition,2012,25(2):90-94. [24]楊甲山.一類二階非線性變時滯差分方程的振動準則[J].中央民族大學學報:自然科學版,2012,21(1):37-41. YANG Jiashan. Oscillation criteria for a class of second order nonlinear difference equation with variable delay[J]. Journal of Minzu University of China: NaturalSciences Edition,2012,21(1):37-41. YANG Jiashan Abstract:We study the oscillatory behavior of a class of second-order nonlinear neutral functional differential equations with variable delay. By using the generalized Riccati transformation and the inequality technique, we establish two new oscillation criteria for the oscillation of the equations. The examples are provided to illustrate that our result gives a sharper estimate for the oscillation of the equations. Key Words:oscillation; variable delay; functional differential equation; Riccati transformation 中圖分類號:O 175.7 文獻標志碼:A 文章編號:1008-9497(2016)03-257-07 作者簡介:楊甲山(1963-),ORCID:http://orcid.org/0000-0002-0340-097X,男,教授,主要從事微分方程的理論與應用研究,E-mail:syxyyjs@163.com. 基金項目:廣西壯族自治區教育廳科研項目(2013YB223);國家青年科研基金資助項目(61503171);梧州學院2014年校級科研重大項目(2014A003);碩士學位授予單位立項建設項目(桂學位[2013]4號). 收稿日期:2015-08-16. DOI:10.3785/j.issn.1008-9497.2016.03.002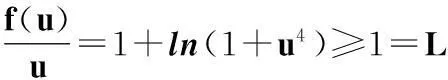

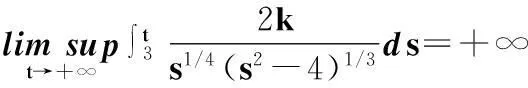

(SchoolofInformationandElectronicEngineering,WuzhouUniversity,Wuzhou543002,GuangxiZhuangAutonomousRegion,China)
Oscillation of certain second-order nonlinear neutral functional differential equations with variable delay.Journal of Zhejiang University(Science Edition), 2016,43(3):257-263

