無線傳感器網絡TPSN-RBS聯合時間同步算法*

姜　帆， 鄭　霖

(1.無線寬帶與信號處理重點實驗室，廣西 桂林 541004；2.桂林電子科技大學 信息與通信學院，廣西 桂林 541004)

?

無線傳感器網絡TPSN-RBS聯合時間同步算法*

姜帆1,2， 鄭霖1,2

(1.無線寬帶與信號處理重點實驗室，廣西 桂林 541004；2.桂林電子科技大學 信息與通信學院，廣西 桂林 541004)

摘要:針對大規模多跳傳感器網絡節點間所存在的同步誤差及其累積誤差問題，提出了一種基于加權最小二乘法的TPSN-RBS聯合時間同步算法。該算法充分利用可監聽到的消息，通過加權最小二乘法估計得到節點邏輯時鐘的時間偏移和頻率偏移的最優解。用Cramér-Rao下界對本算法進行性能分析，同時與TPSN算法進行仿真對比，結果表明:該算法提高了節點間的同步精度，且在節點密集的大規模無線傳感器網絡中，在保證較低通信量的同時降低了累積誤差。

關鍵詞：無線傳感器網絡； 時間同步； 加權最小二乘法

0引言

時間同步是無線傳感器網絡(WSNs) 的一項重要支撐技術，時間同步在很多方面都有廣泛的應用。從目前的研究成果來看，無線傳感的網絡中的時間同步技術主要可以分為基于發送者—接收者的同步 (sender-receiver synchronization,SRS)機制[1]，這種算法單跳同步精度比較高，但是需要多次的時間信息收發，因此,需要較大的通信量和存儲空間。基于接收者的同步(receiver-only synchronization,ROS)[2]，以及基于接收者—接收者的同步 (receiver-recei-ver synchronization,RRS)機制[3]，這些算法很難做到同時兼顧同步精度和能耗，且這些算法的同步誤差隨跳距累積，難以擴展到大規模高密度無線傳感器網絡。針對上述問題，研究者分別從兩方面對時間同步算法進行改進:一是在成對節點間將最優融合估計引入到時間偏移和相位偏移的估計中，如最大似然估計[4,5]、最小二乘估計[6,7]以及卡爾曼濾波[8,9];二是改進全網時間同步協議[10,11]來達到提高時間同步性能的目的。

常用最優融合估計的有：最小二乘估計、線性最小方差估計、極大后驗估計、Bayes估計以及極大似然估計等[12]。最小二乘估計使用的最優指標是使兩側估計的精度達到最佳，估計中不必使用與被估計量有關的動態信息與統計信息。該方法的最大優點是算法簡單，在對被估計量和量測誤差缺乏了解的情況下仍能使用。

本文基于加權最小二乘法，提出了一種無線傳感器網絡TPSN-RBS聯合時間同步算法。它利用傳感器節點時間同步協議(timing-sync protocol for sensor networks，TPSN)的單跳同步精度高的優點和參考廣播同步 (reference broadcast synchronization，RBS) 算法通信量低的優點，同時結合了加權最小二乘估計，對節點的時間偏移和頻率偏移同時進行同步。該算法在降低了通信量的基礎上，提高了單跳同步的精度，并且在大規模網絡中，降低了時間同步的累積誤差。

1算法模型

1.1時鐘模型

節點i的本地時鐘可表示為

(1)

其中，fi(t)為節點i本地時鐘的頻率偏差，t0為初始時刻，Ti(t0)為節點在t0時刻的本地時間。

在每個節點內有一個本地時鐘和邏輯時鐘。同步算法就是要使所有節點的邏輯時鐘值同步。

1.2基于鄰節點信息的時鐘同步模型

本文中的算法結合了TPSN和RBS兩種算法，兼顧了同步精度和通信量，同時降低了集中式網絡層次結構中的累積誤差。

圖1為整體網絡結構;圖2為整體網絡結構中的參考節點和下層節點之間的連接情況，參考節點P和下層節點A，B，C都在彼此的通信范圍內，它是整體網絡結構中的一個典型的上下層節點連接結構。因此，在闡述該算法時，皆以此結構為例。

圖1　整體網絡結構Fig 1　Overall network structure

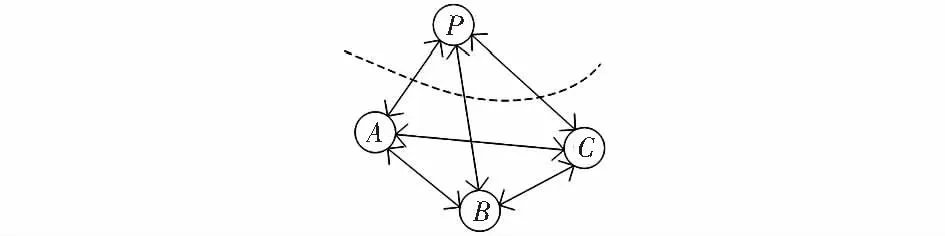
圖2　部分網絡結構Fig 2　Part of the network structure

圖3所示即為時間信息傳播模型，在一個同步周期內的時鐘消息發送情況。下層節點A,B,C分別給在其廣播范圍內的其他節點廣播時鐘信息，接收節點記錄下接收到的消息。在下層節點結束廣播消息時，參考節點P將接收到下層節點的消息時所記錄下的時間廣播發送給下層節點。待同步節點最后收到參考節點發送過來的消息時，同時完成了TPSN算法和RBS算法，最后一個接收到的數據包包含了TPSN算法和RBS算法所需要的信息。

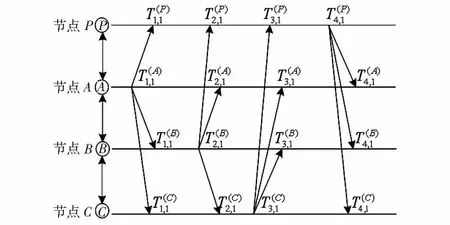
圖3　時間信息傳輸模型Fig 3　Time information transmission model

下面對加權最小二乘估計法在該時間同步算法中的應用進行推導說明。

在時間同步過程中，根據TPSN同步原理，通過節點A和節點P的信息交換，可以得到下面兩個方程

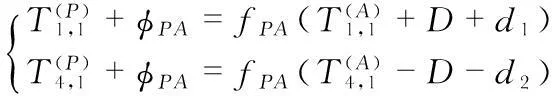
(2)

由上述方程可以推出

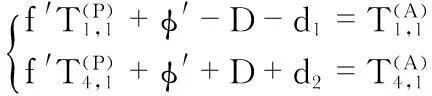
(3)

其中，f′=1/fPA，fPA=fP/fA，φ′=φPA/fPA,φPA=φA-φP，D為傳輸延遲中的固定傳輸延遲，d1和d2為隨機傳輸延遲。

節點A和節點P被動收聽節點B和C廣播的消息，最后節點P把標記的收聽時間發送回給節點A時，對于節點A就可以看作RBS同步過程，根據節點A所得到的時間同步消息，可以得到下面的方程

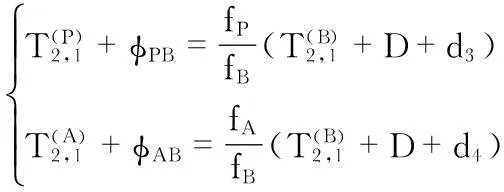
(4)

由上面兩個方程可以推出

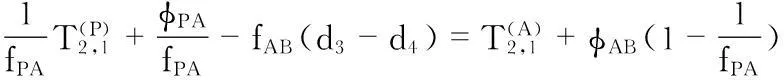
(5)

由于

(6)

式(6)可以寫成

(7)

同理，在節點C廣播時間同步消息時，節點A可以得到一個類似的方程

(8)

因此，通過上述討論，由式(3)、式(7)、式(8)可以得到以下一組方程組

(9)

這是一組關于未知量f′和φ′的矛盾方程組，即方程的數量大于未知量的數量。下面使用加權最小二乘方法對于這個矛盾方程組進行求解。

令

(10)

AX+e=B.

(11)

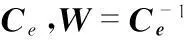
計算得到f′和φ′，對節點中的全局參考時鐘的頻偏和相偏進行校正。

2算法描述

節點i執行的算法迭代過程如下：

1)在初始時刻n=0初始化節點初始頻率相位信息；

2)構建節點網絡，給節點i分配能接收到消息的上層節點和同層節點；

3)在一個時間周期內，從根節點開始，下層節點首先廣播時間同步消息；

4)下層節點廣播消息結束，上層節點廣播時間同步消息；

5)每個下層節點根據記錄的發送時間和接收時間，使用加權最小二乘法同時估計頻偏和相偏；

6)校正本地頻偏和相偏。

3克拉美羅下界分析

在實際應用中，估計的最佳性能可以通過一個下界得到。克拉美羅下界(Cramér-Rao lower bound,CRLB)表述了無偏估計量理論上所能達到的最小方差

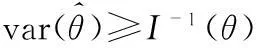
其中,I(θ)為費雪信息量(Fisher information)，定義為

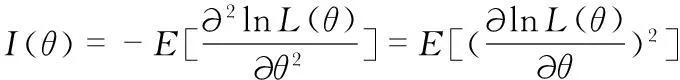
(12)

通常可以利用估計量自身的概率分布函數(probability distribution function,PDF)來計算得到。

在式(11)中，有

式(11)可以寫成e=B-AX,e的協方差矩陣為

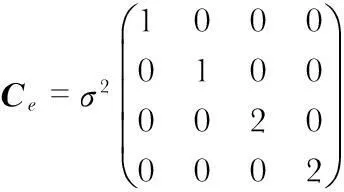
(13)

在未知矢量上，有聯合似然函數

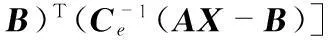
(14)

考慮CRLB，定義矩陣I為

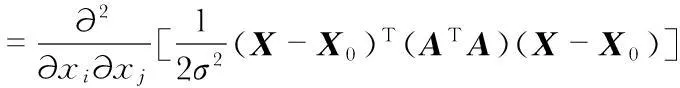
(15)

將上式簡化可得到

I=A-1Ce(AT)-1.

(16)

I為費雪信息矩陣，因此

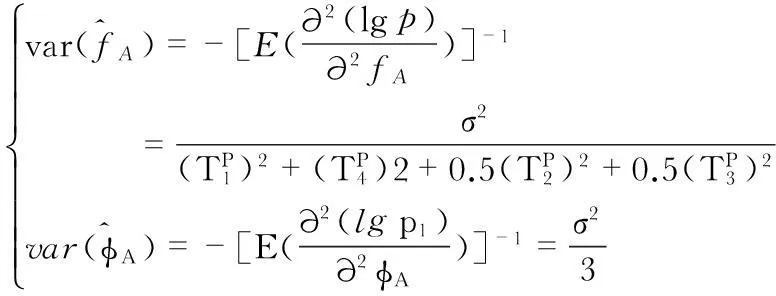
(17)

在式(17)中，頻率偏移估計的均方誤差中包含瞬時時間分量。

4仿真分析

利用Matlab仿真軟件對算法進行數值仿真。該算法從全網同步誤差、多跳累積誤差和通信量三個方面與TPSN算法進行比較。

4.1算法性能比較

圖4為一個6層網絡中節點的連接情況。將位于第1行第1列的節點作為參考節點，觀察全網節點的平均誤差隨時間的變化情況。

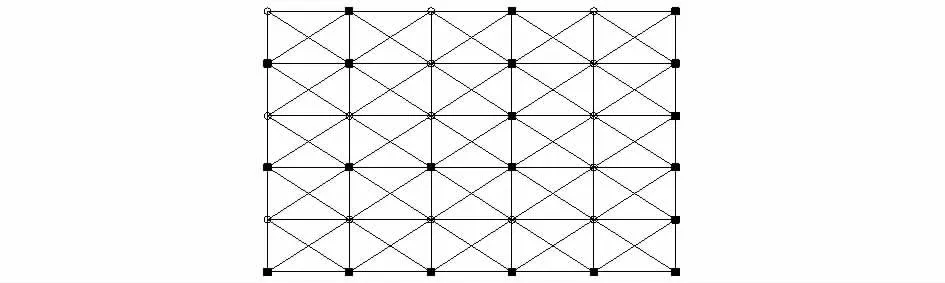
圖4　網絡節點連接情況Fig 4　Connectivity of network node

圖5表示了兩種算法的全網節點誤差的均方誤差(mean square error,MSE)隨著時間同步周期的變化而變化情況。從圖中可以看出，最小二乘時間同步(least square time synchronization,LSTS)LSTS算法的全網節點誤差在經過了一段時間的同步之后，平均誤差趨于穩定，且誤差的MSE為0.1 μs。

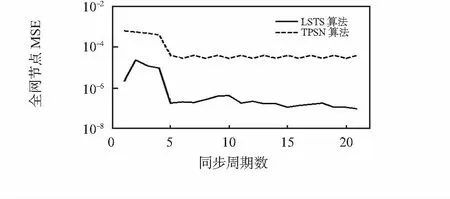
圖5　LSTS算法和TPSN算法全網節點平均誤差的MSE對比Fig 5　Comparison of MSE of entire network nodes averageerror between LSTS algorithm and TPSN algorithm

圖6表示了兩種算法累積誤差的均方誤差的對比，可以看出: LSTS算法的累計誤差比TPSN算法的累計誤差小2個數量級。

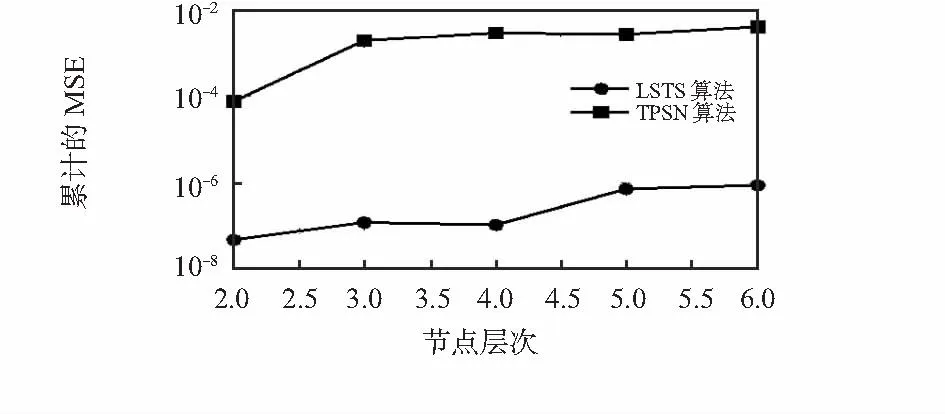
圖6　LSTS算法和TPSN算法累計誤差的MSE對比Fig 6　Comparison of MSE of accumulative error between LSTS algorithm and TPSN algorithm

下面來分析兩種算法在通信量上的對比。從圖4網絡節點連接圖中可以得到在第n層中有2n-1個節點，從第n層節點和第n+1層節點在兩種算法中的通信過程來分析。假設n≥2，在LSTS算法中，在一個同步周期內，每個節點僅廣播一次時間信息消息，那么,LSTS算法的通信量可以表示成(2n-1)+(2n+1)=4n。在TPSN算法中，每個下層節點都要同它的每一個上層鄰節點有一次時間信息交換，由網絡節點連接圖中可以得到n+1層節點與n層節點的連接關系，則TPSN算法的通信量可以表示成2(1+4×2+(2n+1-5)×3)=12n-6。對于全網節點來說，兩種算法的通信量關系也是如此。

從上述分析中可以看出:LSTS算法中是通過廣播的方式來傳遞時間信息，因此，LSTS算法與TPSN算法相比，通信量大大降低。

4.2MSE仿真分析

圖7和圖8分別表示隨著觀測節點層數的遞增，LSTS算法估計的相位偏移和頻率偏移MSE與CRLB的對比。仿真結果表明:LSTS算法估計的相位偏移和頻率偏移MSE隨觀測節點數變化的趨勢與CRLB相同，并且，相位偏移和頻率偏移MSE略大于CRLB。

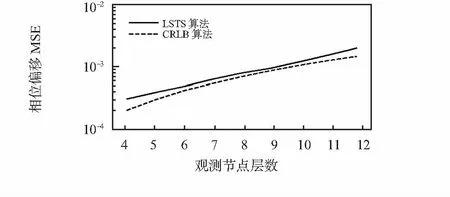
圖7　CRLB和LSTS算法的相位偏移MSE對比Fig 7　Comparison of phase offset MSE between CRLBand LSTS algorithms

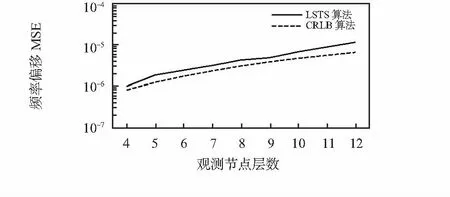
圖8　CRLB和LSTS算法的頻率偏移MSE對比Fig 8　Comparison of frequency offset MSE betweenLSTS and CRLB algorithms

5結束語

信息融合算法對于無線傳感器網絡中同步中相差和頻差的估計具有較高的準確度。本文提出了一種基于加權最小二乘法的TPSN-RBS聯合時間同步算法LSTS。該算法充分利用了可監聽到的時間信息，在單跳同步中具有較高的精度，在大規模多跳網絡中具有較小的累積誤差，與傳統同步算法相比，降低了通信量。

參考文獻:

[1]Ganeriwal S,Kumar R,Sribastava M B.Timing-sync protocol for sensor networks[C]∥Proceedings of the 1st International Conference on Embedded Networked Sensor System,Los Angeles,California,USA,2003:138-139.

[2]Maroti M,Kusy B,Simon G,et al.The flooding time synchronization protocol[C]∥Proceedings of the 2nd International Confe-rence on Embedded Networked Sensor System,Baltimore,USA,2004:39-49.

[3]Elson J,Girod L,Estrin D.Fine-griained network time synchronization using reference broadcasts[C]∥Proceedings of the 5th Symposium on Operating System Design and Implementation,Boston,MA,2002:147-163.

[4]Tian X,Miao Y,Hu T,et al.Maximum likelihood estimation based on time synchronization algorithm for wireless sensor networks[C]∥2009 ISECS International Colloquium on Computing,Communication,Control and Management,CCCM 2009,2009:416-420.

[5]Cao X,Yang F,Gan X,et al.Joint estimation of clock skew and offset in pairwise broadcast synchronization mechanism[J].IEEE Transaction on Communications,2013,61(6):2508-2521.

[6]Chepuri S P,Rajan R T,Leus G,et al.Joint clock synchronization and raning:Asymmetrical time-stamping and passive listening[J].IEEE Signal Processing Letters,2013,20(1):51-54.

[7]Akhlaq M,Sheltami T R. RTSP:An accurate and energy-efficient protocol for clock synchronization in WSNs[J].IEEE Transactions on Instrumentation and Measurement,2013,62(3):578-589.

[8]Xu X,Xiong Z,Sheng X,et al.A new time synchronization method for reducing quantization error accumulation over real-time networks:Theory and experiments[J].IEEE Transaction on Industrial Informatics,2013,9(3):1659-1669.

[9]Giorgi G.An event-based Kalman filter for clock synchro-nization[J].IEEE Transactions on Instrumentation and Measurement,2015,64(2):449-457.

[10] Yildirim K S,Kantarci A.Timing synchronization based on slow-flooding in wireless sensor networks[J].IEEE Transactions on Parallel and Distributed Systems,2014,25(1):244-253.

[11] Chang Q,Zhang M,Yao M.A new energy-efficient timing synchronization protocol in wireless sensor networks[C]∥2014 IEEE International Conference on Computer and Information Technology(CIT),2014:684-688.

[12] 韓崇昭,朱洪艷,段戰勝.多元信息融合[M].北京:清華大學出版社,2006:231-236.

[13] Kyoung-lae Noh,Chaudhari Q M,Serpedin E,et al.Novel clock phase offset and skew estimation using two-way timing message exchanges for wireless sensor networks[J].IEEE Transactions on Communications,2007,55(4):766-777.

[14] Leng M,Wu Y.On cock synchronization algorithms for wireless sensor networks under unknown delay[J].IEEE Transactions on Vehicular Technology,2010,59(1):182-190.

姜帆(1989-)，女，遼寧撫順人，碩士研究生，主要研究領域為無線傳感器網絡。

TPSN-RBS joint time synchronization algorithm for wireless sensor networks*

JIANG Fan1,2， ZHENG Lin1,2

(1.Key Laboratory of Wireless Wideband Communication and Signal Processing, Guilin 541004,China； 2.School of Information and Communication Engineering, Guilin University of Electronic Technology,Guilin 541004,China)

Abstract:A TPSN-RBS joint time synchronization algorithm based on weighted least square method is proposed,aiming at synchronization errors and its calculative errors existing between massive multiple hops sensor network nodes.The optimal solution for the time offset and frequency offset of logical clock of node is obtained by weighted least square method,using messages that can be heard.The Cramér-Rao lower bound is used for performance analysis,and compared with the TPSN algorithm,the simulation results show that,the synchronization precision between nodes is improved,and in large-scale wireless sensor networks with dense nodes,assure lower communication traffic,at the sometime cumulative errors are reduced.

Key words:wireless sensor networks(WSNs); time synchronization; weighted least square method

作者簡介:

中圖分類號：TP 393

文獻標識碼：A

文章編號：1000—9787(2016)01—0149—04

*基金項目：國家自然科學基金資助項目(61362006)；省部共建教育部重點實驗室認知無線電基金資助項目(2013ZR08)；2014年度廣西高校科學技術研究項目(YB2014137)

收稿日期：2015—03—30

DOI:10.13873/J.1000—9787(2016)01—0149—04