采用非線性自回歸時序模型的汽車懸架隔振性能辨識*

陳茹雯　王玉國　湛時時

（南京工程學院，南京210036）

?

采用非線性自回歸時序模型的汽車懸架隔振性能辨識*

陳茹雯王玉國湛時時

（南京工程學院，南京210036）

【摘要】根據攝動法求解非線性微分方程理論，通過單自由度振動系統在單位脈沖激勵下動力學方程的解析解，推導出了振動系統時域響應的非線性自回歸時序（GNAR）模型表達式，獲得了基于GNAR模型的懸架隔振性能主要指標計算公式。通過對某汽車懸架隔振參數辨識的試驗結果表明，基于GNAR模型的懸架隔振性能辨識方法準確、便捷，能實現對在用車輛懸架隔振性能的快速辨識和評價。

1　前言

汽車懸架隔振性能的主要指標是懸架的固有頻率、阻尼比和懸架效率。采用文獻［1］～文獻［7］中的方法能較好地獲得懸架系統特性參數，但也存在一些缺點：如采用解析法求解固有頻率，必須掌握系統工作機理，正確建立其非線性微分方程；采用快速正弦掃頻激振測試結構可能受測試臺和飛輪慣性影響；某些懸架參數在線辨識方法需要特殊的信號發生器和較多的傳感器等。

汽車懸架可視作質量-彈簧-阻尼系統，因此，懸架在外界激勵作用下的輸出是一組能反映系統本身特性的時間序列。非線性自回歸時序（General Expres?sion for Nonlinear Autoregressive，GNAR）模型能以任意精度逼近線性/非線性系統，模型的階數、記憶步長及參數能反映數據系統的固有特性［8，9］，因此本文研究了一種基于GNAR模型的汽車懸架隔振性能快速辨識方法。首先以攝動法求解非線性微分方程的理論為基礎，根據單自由度振動系統單位脈沖激勵下動力學方程的解析解，推導出振動系統時域響應的GNAR模型表達式；然后推導出基于GNAR模型的懸架隔振性能主要指標計算公式；通過Duffing系統自由振動算例，證明非線性GNAR模型與弱非線性系統之間的本質聯系，通過模型的結構和參數可以辨識出系統的非線性特征；最后對某汽車懸架隔振參數進行了辨識試驗。試驗結果表明，該方法準確、便捷，能實現對在用車輛隔振性能的快速辨識和評價。

2　GNAR模型

GNAR模型表達式為：

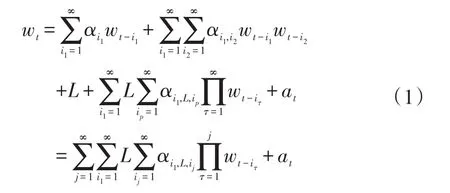
式中，wt（t=1，2，…）為系統輸出數據；at（t=1，2，…）為零均值白噪聲序列；αi1,…,αi1,i2,…為模型參數。

實際建模時，模型階次一般取為有限值，式（1）改寫為：

該模型可以簡記為GNAR（p；n1, n2,…, np）。

3　基于GNAR模型的振動系統辨識原理

3.1弱非線性振動系統剛度和阻尼的辨識

單自由度質量-彈簧-阻尼系統如圖1所示，設系統相對于平衡位置的位移響應為z（t），根據牛頓第二定律，其運動微分方程為：

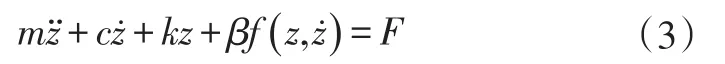
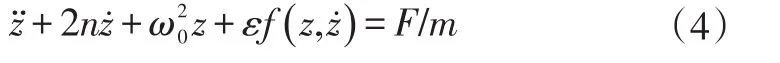
當ε=0時，方程（4）成為：

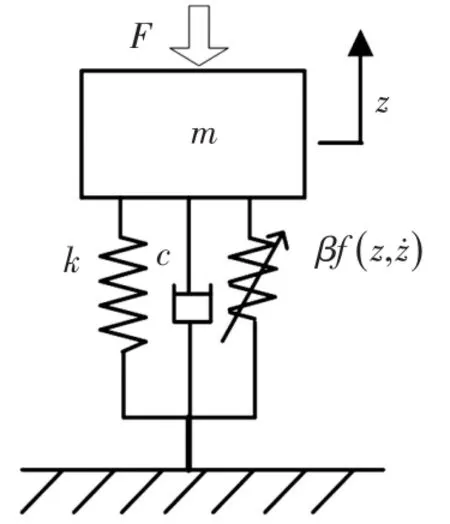
圖1　質量-彈簧-阻尼系統

方程（5）是方程（4）的派生方程，描述線性簡諧振動，若系統在t=0時刻受到單位脈沖力F=1δ（t）輸入，則方程（5）的解為［11］：

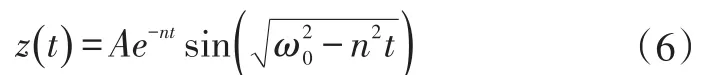
對式（6）所示的函數值z進行等間隔離散采樣，得到一組時間序列zi，i=1, 2,…，在任意時刻有：

設定采樣間隔為Δt，由此可得：

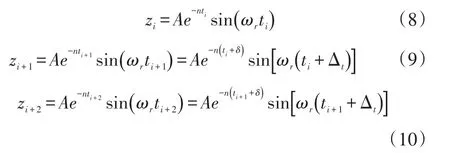
利用三角函數公式將式（9）和式（10）展開，進行恒等變換，可得：

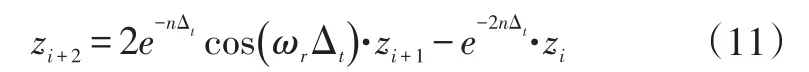
式中，Δt為采樣間隔，可以視作常數。

可見，單自由度線性系統自由振動的時域響應可以采用GNAR（1；2）表示。

GNAR（1；2）的系數α1和α2為：

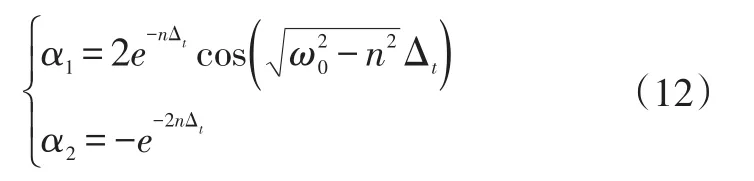
當ε≠0時，根據攝動法求解非線性微分方程的原理［12］，方程（4）所示自治振動系統的解z和非線性頻率ω可以寫為：

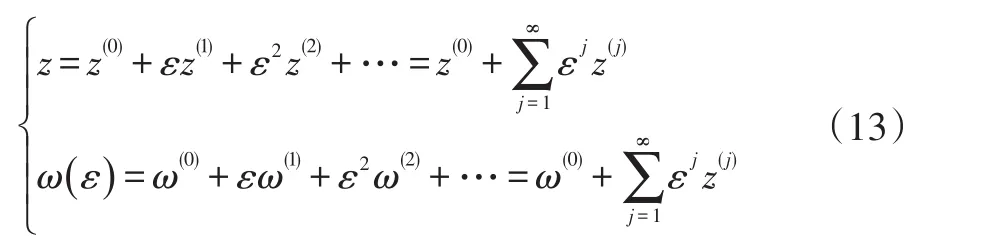
式中，右端各項表示方程解不同量級的項，z（0）、ω（0）表示零級項，且稱為j級項。

將式（13）代入方程（4），根據等式左右同一量級相等原則，可以寫出各級解滿足的方程：

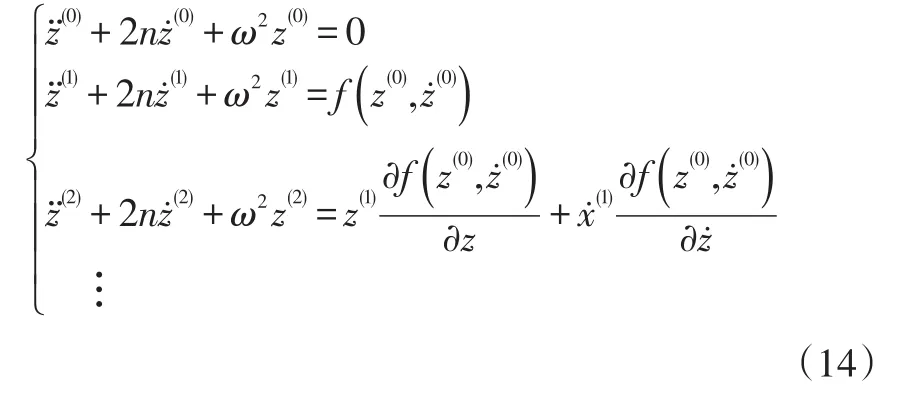
式中，各等式分別表示零級方程、一級方程、二級方程…。

顯然，式（14）中的零級方程就是派生方程（5），因此零級解可表示為：

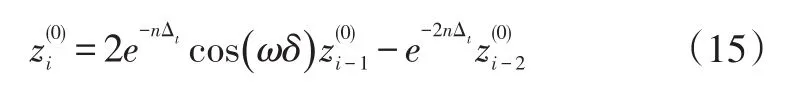
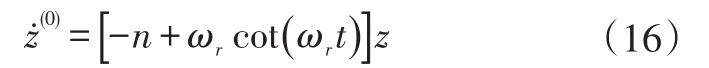
將式（16）代入式（14）中一級方程的右端：

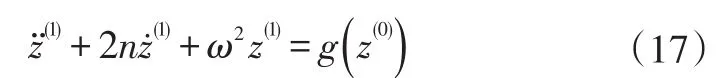
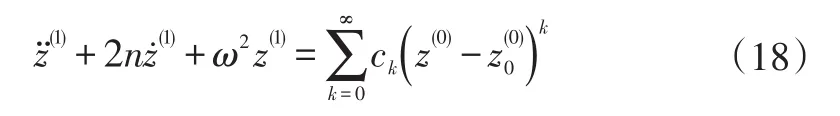
式中，z（0）和ck為常數。

因此，一級解z（1）可以寫成關于z（0）的多項式：

式中，P1表示多項式函數。

將式（15）代入式（19）：

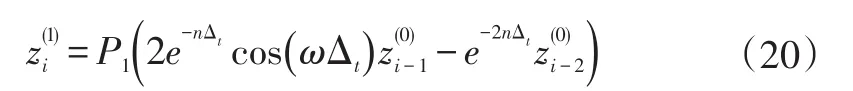
對式（19）所示的z（1）求導數，可以得到和：

將式（19）和式（21）代入式（14）中二級方程的右端，可以獲得i時刻的二級解表示為零級解和的高階多項式形式，用P2表示。同理可以求得二級以上各階解。

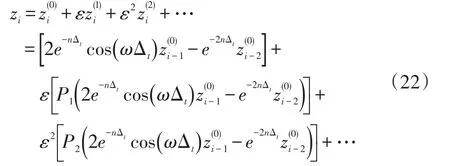
式中，多項式函數Pi取決于方程（4）的非線性解析函數f。

根據式（13）有：

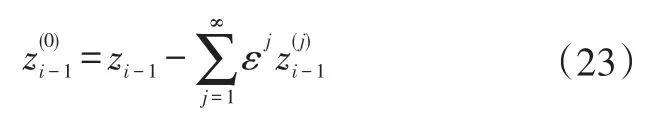
將式（23）代入式（22）：

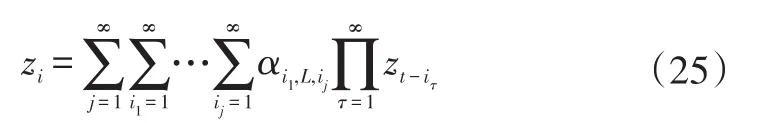
式中，αi1,L,ij為待定系數。

式（25）表明非線性系統現時刻的輸出值可以用過去時刻輸出值的高階多項式來表示，這與GNAR模型的表達形式一致。可見，非線性GNAR模型可以用來描述非線性系統輸出，模型系數由系統基本參數（如參數ω0、非線性量ε）確定。

觀察式（24）的右側可以發現，右側第一項中zi-1和 zi-2的系數為和e-2nΔt；從右側第二項開始，zi-1和zi-2的系數都是包含的乘積項，當ε是正的常數時，隨著j增大因此，式（25）的系數為：

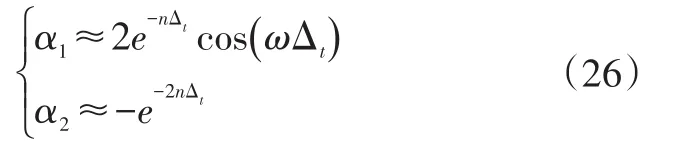
變換式（26），可以得到系統參數：

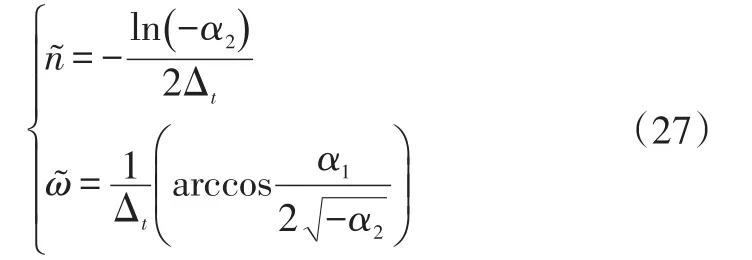
式（27）的含義是在弱非線性條件下采用零級頻率分量表示系統非線性頻率。

上述推導過程針對的是系統位移輸出，同樣方法可以推導出速度、加速度輸出的GNAR模型表達方式。因此，對未知參數的單自由度振動系統輸出的位移、速度或加速度信號建立GNAR模型，獲得模型的參數α1和α2后，通過式（28）可以算出系統相關參數。

3.2仿真算例

Duffing系統的自由振動方程物理意義是一種具有漸硬彈簧的振動系統：

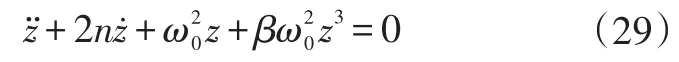
式中，n表示系統衰減系數；ω0為頻率參數；β為正的常數表示非線性彈力。

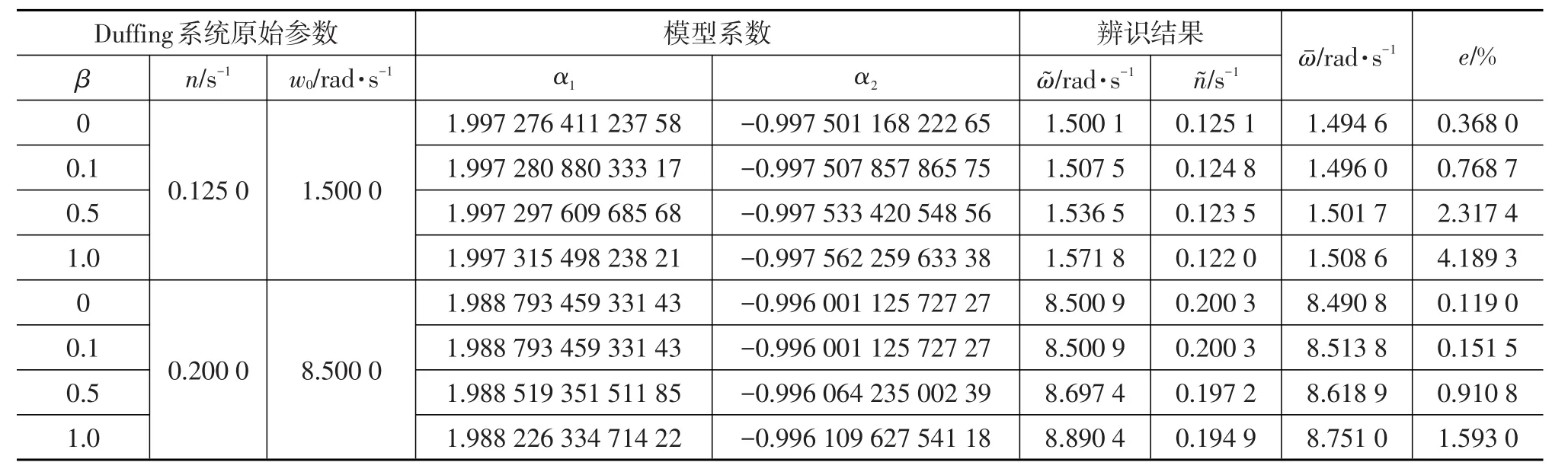
表1　Duffing系統辨識結果

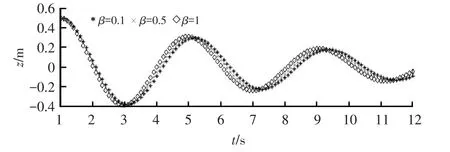
圖2　Duffing系統振動位移輸出序列（系統參數n=0.125/s，w0=1.5 rad/s）

對系統輸出建立GNAR模型，根據式（27）辨識出n? 和?，試驗結果列于表1。表1中是系統輸出的10個周期的均值，相對誤差e為：

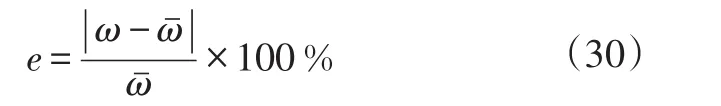
從表1中可以看出，辨識結果的相對誤差在5％以內，較為準確。隨著β增大，非線性頻率增大，其原因為系統的非線性恢復力隨著β增大而增大，這與圖2所示序列的變化趨勢一致。

可見，GNAR模型可以用來描述非線性系統，且通過模型的結構和參數可以辨識出系統的非線性特征參數。

4　汽車懸架隔振性能辨識方法的應用

4.1懸架隔振參數的辨識

將懸架簡化為圖1所示單自由度質量-彈簧-阻尼系統，根據機械振動理論，懸架的固有頻率fd、阻尼比ξ和懸架效率η這3項指標的理論計算公式為：

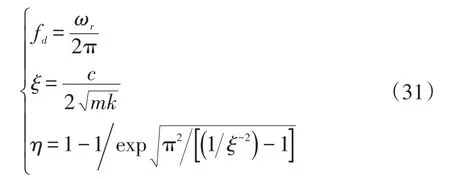
式中，m為汽車簧載質量；k為懸架系統剛度；c為懸架系統阻尼；ωr為懸架的阻尼固有頻率

將式（27）和式（28）代入式（31），即采用GNAR模型的參數α1和α2表示懸架的固有頻率和阻尼比：

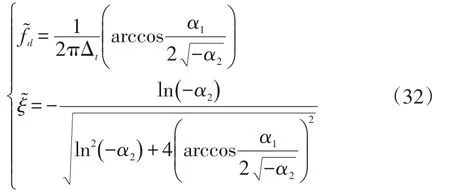
4.2辨識試驗

單輪平板式汽車懸架參數檢測平臺硬件組成如表2所列。采用按壓車體法給予被測車輛擬脈沖激勵，由單輪平板式汽車懸架參數檢測平臺采集車體駕駛室在擬脈沖激勵下的振動加速度信號，如圖3所示。實際采樣時長為10 276 ms，通道采集點數為512個，通道采樣頻率為49.822 Hz。

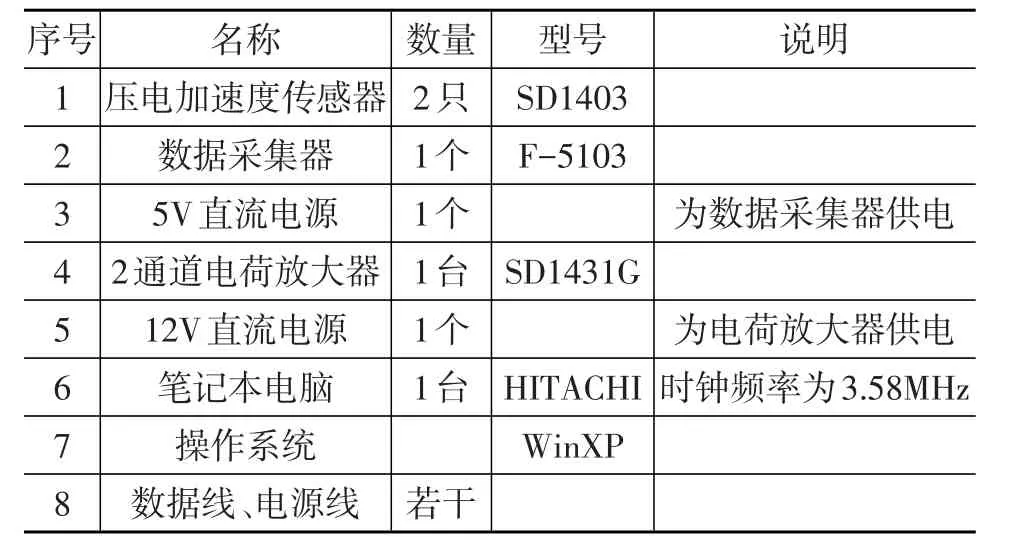
表2　單輪平板式汽車懸架參數檢測平臺硬件組成

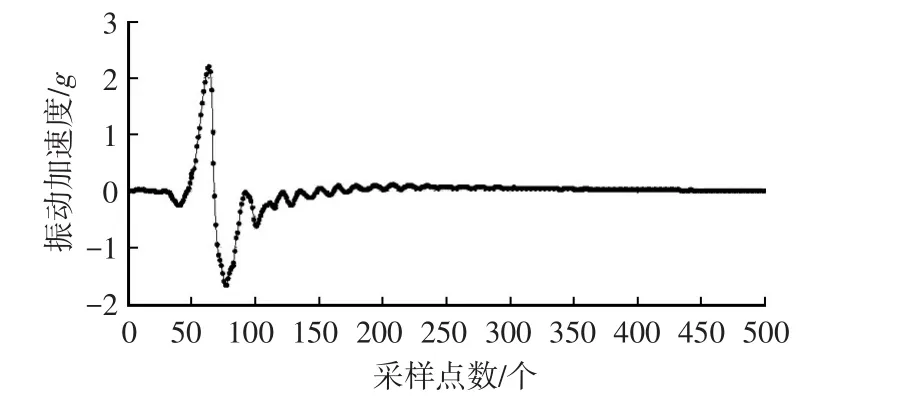
圖3　振動加速度信號

對振動加速度信號建立GNAR模型，獲得模型參數α1和α2，根據式（31）和式（32）即可得到懸架系統的3個隔振性能指標。表3給出了5次試驗的辨識結果，可以看出基于GNAR模型辨識出的懸架隔振性能參數接近于設計值。

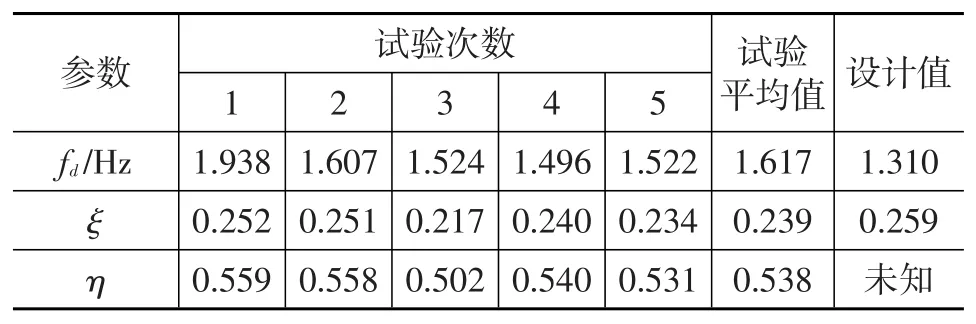
表3　試驗車懸架參數辨識結果

根據國家標準和歐洲減振器協會EUSAMA的要求，汽車懸架阻尼比ξ的值應在0.2～0.45之間，懸架效率η應大于0.45，懸架的固有頻率fd應盡可能在人體感覺較為舒適的1.0～1.6 Hz之間。對照標準，可知該車懸架隔振性能合格。

5　結束語

提出了一種基于GNAR模型的汽車懸架隔振性能快速辨識方法，即給予被測車輛懸架擬脈沖激勵，根據懸架振動輸出信號建立GNAR模型，根據模型系數可以辨識出懸架的隔振性能指標。理論推導與Duffing自由振動系統算例證明了由GNAR模型的結構和參數可以辨識出系統的線性或非線性特征及相關參數，因此，該辨識方法對線性和非線性懸架系統都適用。

GNAR模型只對觀測到的系統輸出的有序數據進行分析和處理，模型中包含線性和非線性項，建模時不需要進行平穩性檢驗和數據預處理，建模便捷，因此，該辨識方法無需掌握被測車輛的具體結構，可實現對在用車輛隔振性能的快速辨識和評價。

參考文獻

1張雨.汽車懸架振動試驗臺垂向主振動的有效性分析.振動、測試與診斷, 2010, 30（4）: 455～457.

2方瑞華.汽車空氣懸架非線性振動理論和試驗.農業機械學報, 2007, 38（7）: 13～15.

3唐駕時,唐應時.非線性懸架系統固有頻率的計算.汽車技術, 1986,（9）: 13～18.

4余卓平，陸雄華.非線性懸架系統頻率特性數值解.上海汽車, 1998, 5（2）: 36～38.

5R Majjad. Estimation of Suspension Parameters// Proceed?ings of the 1997 IEEE International Conference on Control Applications. Hartford, USA, 1997: 522～527.

6張亮亮,唐駕時,李立斌.虛擬激勵算法下的汽車懸架振動分析.振動與沖擊, 2006, 25（6）: 167～169.

7張慧杰,郭志平,司景萍,等.汽車懸架整車動力學模型的參數辨識.振動與沖擊, 2013, 32（23）: 145～150.

8陳茹雯,黃仁,史金飛,等.線性/非線性時間序列模型一般表達式及其工程應用.東南大學學報:自然科學版, 2008, 38（6）:1077～1080.

9 Ren H, Feiyun X, Ruwen CH. General expression for linear and nonlinear time series models. Frontiers of Mechanical Engineering in China, 2009, 4（1）: 15～24.

10聞邦椿,劉樹英,陳照波,等.機械振動理論及應用.北京:高等教育出版社, 2009.

11陳樹輝.強非線性振動系統的定量分析方法.北京:科學出版社, 2009.

（責任編輯簾青）

修改稿收到日期為2015年11月1日。

主題詞:非線性自回歸時序模型懸架隔振性能辨識

Identification of Vehicle Suspension Anti-vibration Performance Based on GNAR Model

Chen Ruwen, Wang Yuguo, Zhan Shishi
（SNanjing Institute of Technology）

【Abstract】First, based on the perturbation method of solving nonlinear differential equation theory, general expression for nonlinear autoregressive（GNAR）model is derived for vibration system time domain response with unit pulse excitation and the calculation formulas of vehicle suspension anti-vibration performance indexes are obtained based on parameters of GNAR model. Finally the vehicle suspension vibration isolation parameter identification experiments are carried on, the results show that the method is accurate and convenient to realize a rapid identification and evaluation of the suspension vibration isolation performance for vehicles in use.

Key words:GNAR model, Suspension, Anti-vibration performance, Identification

*基金項目：國家自然科學基金項目（51305194）；江蘇省自然科學基金項目（BK20130746）。

中圖分類號:U463.33

文獻標識碼:A

文章編號:1000-3703（2016）04-0031-05