電纜電氣參數不同計算方法及其比較

蔣彥波　史記　蔣彥韜

摘要：電纜電氣參數的計算一直都是人們所研究的重要問題。在具體計算過程中，為了能夠更加簡單、直觀、方便地完成對電纜電氣參數的計算，針對不同的電纜電氣參數算法進行了對比與介紹，通過對比找出最佳的算法供人們使用，從而使工程施工變得更加簡單。

關鍵詞：電纜電氣；計算方法；參數計算；工程施工；聯網；供電 文獻標識碼：A

中圖分類號：TM246 文章編號：1009-2374（2016）20-0072-02 DOI：10.13535/j.cnki.11-4406/n.2016.20.035

進入21世紀后，全球經濟和科技都得到了飛速發展，并且隨著人們環保意識的提高，新能源的應用得到了進一步推廣。目前，聯網和供電是人們生活中不可或缺的兩部分，而聯網與供電二者在具體實施過程中，都需要以電纜作為載體。同時，電纜具有占地面積小、可靠性高、搭設簡單、信息傳輸快等多項優點，因此在許多領域都得到了廣泛的應用。在應用電纜過程中，要做好電氣參數計算與分析，這對電纜的應用有著重要影響。

1 各種電纜電氣參數算法介紹

1.1 方法一

對電纜在應用過程中，利用多導體對構建電纜的電路模型進行科學分析，如果在電纜的實際應用過程中，沒有鎧裝層存在，那么在實際操作中，本應當由3根單芯電纜所構成的輸電線路，則會包含6根導體以及與大體進行連接。需要注意的是，這6根導致相互之間要保護平行，同時每根導體要與地面保持平行。阻抗矩陣型的計算原理如下：如果在分析過程中dij≤0.135DcA，在具體計算過程中則可以對Carson-Clem公式進行應用，彎沉對電纜阻抗矩陣的計算，單位為Ω/km。

在式（1）和式（2）中，ri表示的為單位導體內電阻值的大小，在具體計算過程中，需要對鄰近效應和集膚效應進行充分考慮，如果再對導體進行分割處理，那么在具體操作過程中，如果對導體進行上漆處理，可以有效地降低各種效應的發生情況。通常來說，在上述公式中的DCA=660，這也被稱“Carson深度”，而在這個小公式中，表示土壤的電阻率的，單位為Ω·m；表示頻率，單位為Hz；dij表示兩個相鄰導體之間的距離，單位為m。

1.2 方法二

電纜電氣參數的計算也可以通過Matlab中的power cableparam功能完成，通過相關圖形用戶界輸入相應的參數，從而獲得電纜的ELC矩陣。下面針對power cableparam電纜參數的計算方法進行重點介紹：

在式（3）中，RC（dc）表示通過導體的直流電阻；RC（E）表示導體的大地的回流電阻值，通過實際測量可知，該數值的大小為π2×104f，單位為Ω/km；

k1=0.0529f/（3.048×60），表示頻率因數，單位為Ω/km；De=1650為導體是等效大體回路的距離，單位為m；GMR表示導體的幾何半徑大小，單位為m。

在計算過程中線芯之間的阻抗計算如式（4）所示：

式（4）中的GMD表示相鄰導體之間幾何的平均距離，其中n表示所有導體間距的總數，通常來說，并不需要利用此公式完成對GMD的計算，而是作為輸入參數直接獲取。

護套自阻抗的計算通過式（5）完成：

在式（5）中，Dn表示內絕緣層和相導體平均半徑之間的距離大小，單位為m。

護套間與線芯之間的電阻為：CCS=。在上述公式中，假定是XLPE絕緣層，εCS表示內絕緣層的相對介電常數；dia、doa分別表示內絕緣層和外絕緣層半徑的大小，單位為m。

1.3 方法三

交流電阻計算，在電纜中導體與護套之間電阻的計算應當依據式（6）進行計算。

在式（6）中，R（ac）以及R（dc）表示的為電纜導體，后者為護套中的交流電或直流電，電阻值的大小，單位為Ω。在具體計算過程中，對于三芯、雙芯、單芯不同類型的電纜來說，y值都應當取1。如果電纜屬于管道類型，y的取值將會有所變化，通常應當為標準取值的1.5倍，因為常規取值為1，因此在管道電纜中，y的取值應當為1.5。在式（6）中，ks表示集膚效應系數，而kp表示相鄰近效應系數。在具體計算過程中，電路中直流電阻的計算如式（7）所示：

在式（7）中，ρ表示整條電力電阻率的大小，單位為Ω·m；A表示電纜導體標截面面積的大小，單位為m2；θ表示電纜運行過程中，電纜的溫度，單位為℃。

2 三種方法的計算結果與對比

對電纜電氣參數的三種計算方法進行了詳細介紹，下面采用不同方法進行計算，獲取的電感、電阻、電容部分參數，在具體操作過程中，電纜的排列方式的種類有很多，主要針對帶鎧裝電纜和不帶鎧裝電纜兩種情況進行下，1根三芯電纜或3根單芯電纜程等邊三角形的排列的情況機型對比分析。

2.1 沒有鎧裝層電纜

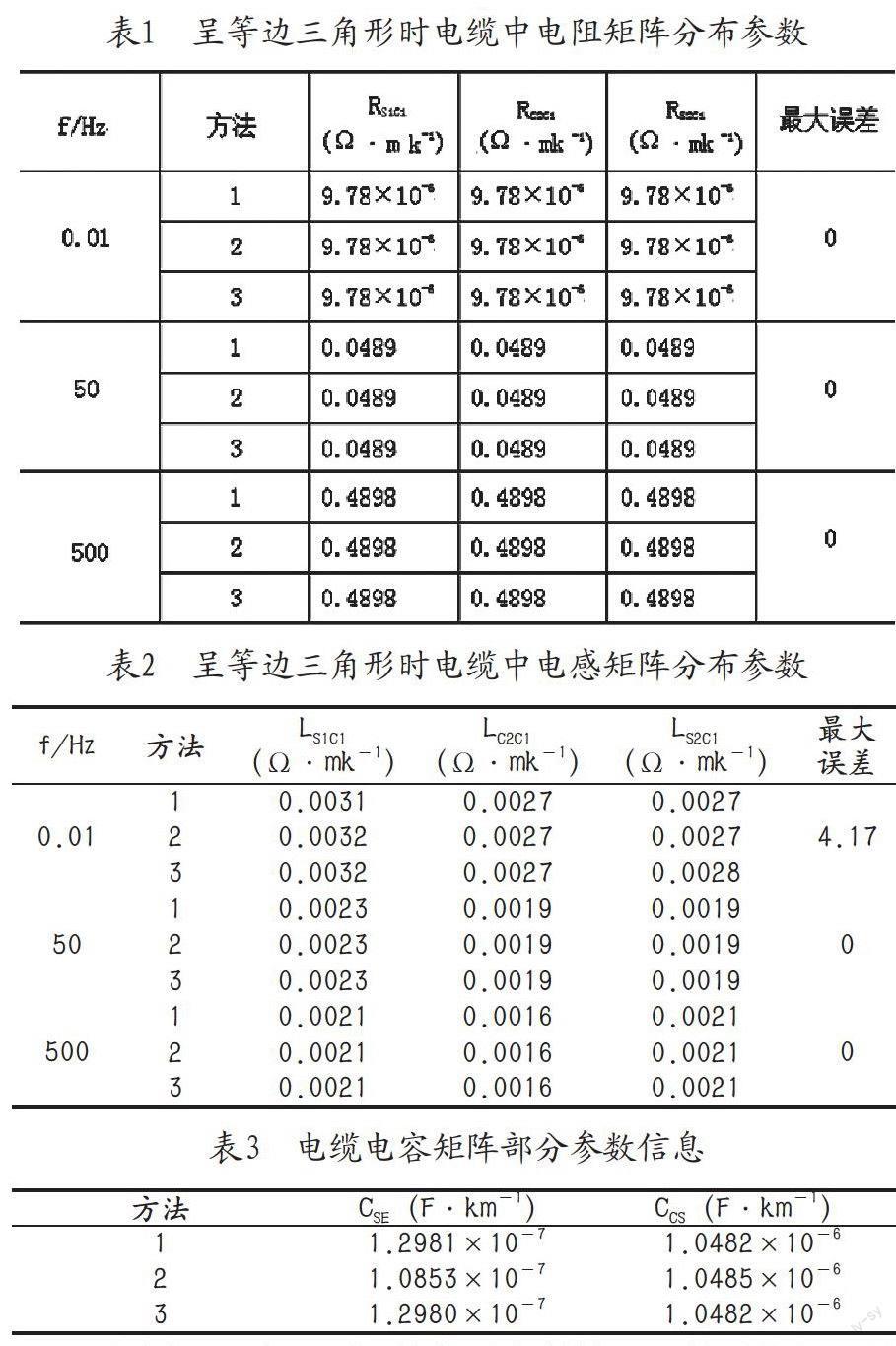
沒有鎧裝層電纜呈等邊三角形排列時，3根電纜之間距離完全相同，表1為3種不同計算方法下，得到的電阻矩陣中的部分參數；表2中表示的則為電感矩陣中的部分參數，在表中，C表示導體，S表示護套，下腳標表示導體的具體編號，例如S2C1表示為2號電纜的護套與1號電纜導體之間的互電感或互電阻。電纜電容的矩陣參數詳細信息如表3所示：

通過表1、表2、表3將各項參數輸入，然后依據阻抗推導公式，對沒有鎧裝的等邊三角形序列的阻抗進行計算，通過計算結果可知，正序阻抗和負序阻抗兩者的數值相等，并且在正序電感和零序電感達到一定頻率后，兩者的數值趨近相等，但是如果在具體電纜鋪設過程中，電纜為平鋪，正序電感和零序電感的頻率范圍將會存在較大差距。

2.2 鎧裝電纜

在對鎧裝電纜進行分析時，假設鎧裝層的材料為鋁，開組層的內徑大小為0.0689m，外徑的大小為0.07988m，電阻率的大小為3×10-8m，對電纜的橫截面積進行量測，通過量測得到電纜橫截面積大小為0.0028m2，電纜的相對磁導率大小為1.5，電纜外層的橡膠互層的厚度為0.003m，相對介質常數大小為2.5。其余參數，例如護套、線芯等，都與沒有鎧裝電纜的參數相同。表4、表5分別對比了方法二和方法三兩種計算方法所獲得的電阻、電容參數，這主要因為power cablepram算法不能用于對沒有鎧裝電纜參數的計算。

3 結語

綜上所述，電纜電氣參數計算過程中可以采用不同的方法進行，不同的計算方法取得的效果不同。本文主要分析了三種不同的計算方法，從電纜電氣參數計算的準確性和便捷性來看，在計算中應用方法一是最佳選擇。

參考文獻

[1] 甘啟才.電力電纜電氣參數及電氣特性研究[J].中國高新技術企業，2016，（3）.

[2] 李婧，郭金明，黃鋒.用于電力電纜現場測試的電氣參數及接頭位置識別裝置的研制[J].低碳世界，2015，（31）.

[3] 杜伯學，李忠磊，張鍇，王立.220kV交聯聚乙烯電力電纜接地電流的計算與應用[J].高電壓技術，2013，（5）.

[4] 鄭雁翎，王寧，李洪杰，張冠軍.電力電纜載流量計算的方法與發展[J].電氣應用，2010，（3）.

[5] 成凌飛，王泰華.礦用通信電纜基本電氣參數數值模型[J].電工技術學報，2010，（12）.

[6] 唐忠，高巍.單芯XLPE電纜分布參數的研究與計算

[J].華東電力，2014，（3）.