基于相平面法的同步Buck變換器動態分析

周小林

摘要：相平面法可以直觀清晰地反映系統的動態過程及性能，現有的Buck變換器分析過程大部分基于微分方程，分析過程欠直觀。文章利用相平面法對Buck變換器進行分析，選取電流和電壓作為相平面坐標，分析其電流和電壓的變化過程。該方法計算簡單、概念清晰，可以直觀地反映電流和電壓的變化過程。

關鍵詞：Buck變換器；非線性系統；相平面法；微分過程；相平面坐標 文獻標識碼：A

中圖分類號：TM133 文章編號：1009-2374（2016）20-0062-02 DOI：10.13535/j.cnki.11-4406/n.2016.20.030

1 概述

相對于傳統的線性電源，開關電源具有轉換效率高、輸入電壓范圍大、輸出電壓穩定等優點，廣泛應用于工業控制、電力系統等領域。開關電源的拓撲形式多種多樣，其中Buck變換器是最為簡單且具代表的一種，已應用于光伏并網、LED和電池充電等領域。雖然Buck變換器應用廣泛，但其分析過程大部分是基于微分方程的，分析過程欠直觀，難于工程應用。

相平面法是分析非線性系統的一種常用方法，通過相平面圖直觀清晰地反映系統的動態過程及性能，其計算簡單、概念清晰，非常適合于工程應用。

本文利用相平面法對同步Buck變換器的動態過程進行分析，選取具體的物理量為相平面坐標軸，通過相平面得到Buck變換器中變量的變化趨勢，為后續的分析設計提供依據。

2 同步Buck變換器模型

Buck變換器的原理圖如下：

當開關S1、S2處于不同狀態時，該電路有不同的動態特性，該系統屬于切換系統，其數學模型如下：

當S1閉合、S2斷開時，Buck變換器的狀態空間模型

如下：

當S1斷開、S2閉合時，Buck變換器的狀態空間模型如下：

式（1）、式（2）中：L表示電感感量；C表示輸出電容容量；R表示負載電阻阻值；iL表示電感電流；vi表示輸入電壓；vo表示輸出電壓。

當電路正常工作時，以上兩種狀態不停切換，其整體呈現出來的動態特性就是以上兩種特性的疊加。

3 Buck變換器的相平面模型及其動態分析

若對同步Buck變換器直接套用傳統的相平面法，則獲得輸出電壓及其導數構成的相平面，與實際物理量不存在直接對應的關系。為了獲得物理意義明確的相平面圖，這里選擇實際物理量作為相平面坐標，使相平面更加直觀清晰。對上述的同步Buck模型，選取vo為橫坐標、iL為縱坐標，則相平面中的曲線斜率如下：

當S1閉合、S2斷開時，相平面中的斜率為：

當S1斷開、S2閉合時，相平面中的斜率為：

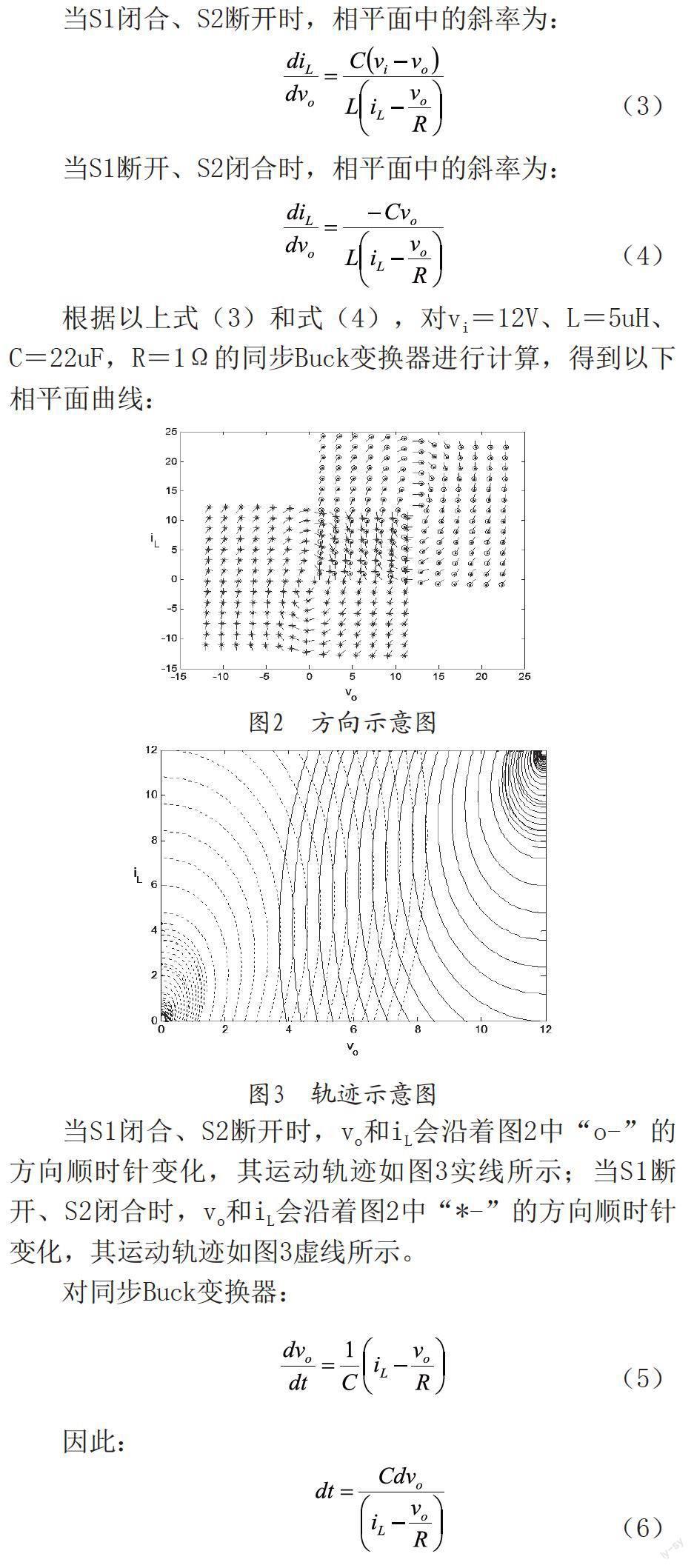
根據以上式（3）和式（4），對vi=12V、L=5uH、C=22uF，R=1Ω的同步Buck變換器進行計算，得到以下相平面曲線：

當S1閉合、S2斷開時，vo和iL會沿著圖2中“o-”的方向順時針變化，其運動軌跡如圖3實線所示；當S1斷開、S2閉合時，vo和iL會沿著圖2中“*-”的方向順時針變化，其運動軌跡如圖3虛線所示。

對同步Buck變換器：

式中：Δvo代表上述兩點間的vo的差；代表兩點間的平均電壓；兩點間的平均電流。

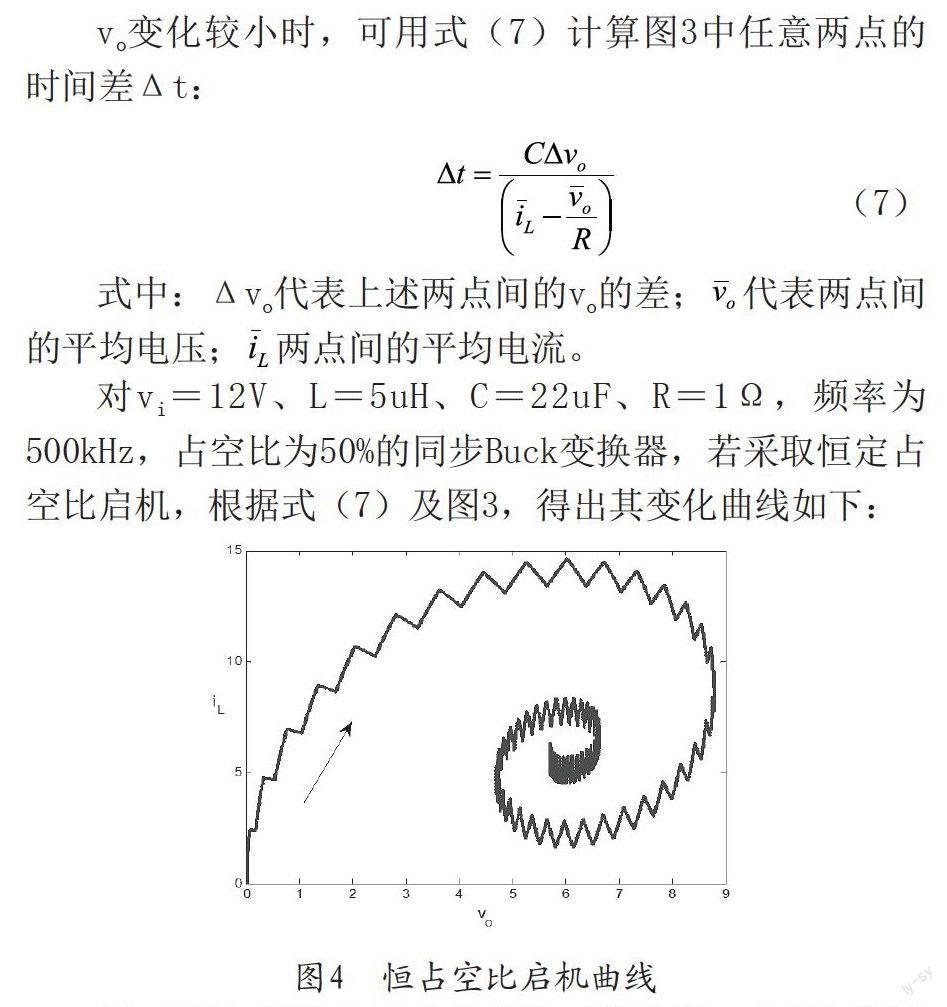
對vi=12V、L=5uH、C=22uF、R=1Ω，頻率為500kHz，占空比為50%的同步Buck變換器，若采取恒定占空比啟機，根據式（7）及圖3，得出其變化曲線如下：

圖4反映了同步Buck變換器啟動的過程。由于占空比為50%，因此輸出電壓穩定值為6V。vo從0V變化到8V，然后下降到6V，iL從0A上升到14A，然后回落到6A。

根據以上相平面圖，可以直觀地分析出vo和iL的變化過程，確定vo和iL的變化范圍和變化趨勢，為方案設計和元器件選擇提供依據。

4 結語

本文利用相平面法對Buck變換器進行分析，選取電流和電壓作為相平面坐標，分析其電流和電壓的變化過程，計算簡單、概念清晰，可以直觀地反映電流和電壓的變化過程。除了Buck變換器外，該方法還可以推廣到boost、Buck-boost等二階變換器。

參考文獻

[1] 嵇保健，洪峰，趙劍鋒.一種不隔離三電平雙Buck光伏并網逆變器[J].中國電機工程學報，2012，32（12）.

[2] 閻鐵生，許建平，曹太強，等.基于二次型BuckPFC變換器的無頻閃無變壓器LED驅動電源[J].電工技術學報，2015，30（12）.

[3] M.G.Kim.Proportional-Integral Compensator Design of Duty-Cycle-Controlled Buck LED Driver[J].IEEE Transactions on Power Electronics，2015，30（7）.

[4] Ying-Chun Chuang.High-Efficiency ZCS Buck Converter for Rechargeable Batteries[J].IEEE Transactions on Industrial Electronics，2010，57（7）.

[5] L.Shi，B.P.Baddipadiga，M.Ferdowsi，M.L.Crow.Improving the Dynamic Response of a Flying-Capacitor Three-Level Buck Converter[J].IEEE Transactions on Power Electronics，2013，28（5）.

[6] 胡壽松.自動控制原理（第六版）[M].北京：科學出版社，2013.

[7] K.Sun，S.T.Lee，P.Zhang.An Adaptive Power System Equivalent for Real-Time Estimation of Stability Margin Using Phase-Plane Trajectories[J].IEEE Transactions on Power Systems，2011，26（2）.