蘭州市財政收入與GDP的協(xié)整分析與誤差修正模型研究
王玉芳


摘要:利用協(xié)整理論對蘭州市1978-2013年的財政收入和GDP的關(guān)系進行實證分析,結(jié)果表明,蘭州市財政收入和GDP相關(guān)度較高,整體上存在長期穩(wěn)定的協(xié)整關(guān)系,二者的動態(tài)調(diào)整機制可自動實現(xiàn)長期均衡;Granger因果檢驗表明,財政收入和GDP間存在單向因果關(guān)系,即GDP的增長是蘭州市財政收入增長的決定因素。
關(guān)鍵詞:協(xié)整分析;Granger因果檢驗;誤差修正模型
中圖分類號:F127 文獻識別碼:A 文章編號:1001-828X(2016)009-000-02
一、引言
作為實現(xiàn)政府職能和協(xié)調(diào)收入分配的重要保障,財政收入通常包括地方財政收入和中央財政收入,是衡量一個地區(qū)或國家的財力和經(jīng)濟發(fā)展水平的重要指標(biāo)[1]。國內(nèi)生產(chǎn)總值(GDP)是一個地區(qū)或國家在一定時期內(nèi)國民經(jīng)濟活動最終成果的總量指標(biāo),反映經(jīng)濟發(fā)展的綜合水平。財政收入的影響因素主要有經(jīng)濟發(fā)展水平、收入分配政策和物價水平。本文以蘭州市為例,重點研究財政收入與GDP即經(jīng)濟發(fā)展水平間的關(guān)系。
目前,國內(nèi)學(xué)者對GDP和財政收入關(guān)系的研究主要集中在增長速度的比較和二者關(guān)系的探究。何凌云等(2013)[2]對財政收入增速超過經(jīng)濟增長增速的問題進行了統(tǒng)計分析;林國立等(2015)[3]基于GDP與財政收入間的關(guān)系,對蚌埠市財政收入和GDP增幅的差異性進行分析。王玉華等(2009)[4]對山東省財政收入和GDP進行時間序列分析,認(rèn)為二者存在長期穩(wěn)定關(guān)系;文秀琴(2013)[5]對河南省財政收入和GDP進行相關(guān)分析,證明二者存在一元線性回歸關(guān)系。本文采用協(xié)整理論,深入分析蘭州市財政收入和GDP間的關(guān)系,并建立誤差修正模型。
二、研究方法
(一)單位根檢驗
單位根檢驗主要用于檢驗變量的平穩(wěn)性并推斷其單整階數(shù),常用的方法包括ADF檢驗、DF檢驗和PP檢驗。本文采用使用最廣泛的ADF檢驗,其原理是將因變量的滯后差分項加入回歸方程以控制高階序列相關(guān),基本模型為:
式中,xt為時間序列,t為時間趨勢因素,Δ為一階差分,n為最佳滯后階數(shù),為白噪聲。原假設(shè):H0: λ=1,即{xt}有一個單位根(非平穩(wěn))。本文采用AIC準(zhǔn)則確定最佳滯后階數(shù)n,并使用Mackinnon臨界值判定序列的平穩(wěn)性。
(二)協(xié)整檢驗
協(xié)整檢驗用于確定變量間是否存在長期穩(wěn)定的均衡關(guān)系,主要方法包括Engle-Granger兩步法和Johansen檢驗法。Engle-Granger兩步法適用于兩變量的協(xié)整分析,而Johansen檢驗法常用于多變量的協(xié)整分析,且可求出變量間可能存在的多種協(xié)整關(guān)系。因財政收入和GDP僅為兩變量,故本文采用Engle-Granger兩步法。設(shè)有一階單整變量{yt}與{xt},首先對其進行協(xié)整回歸:
其次,檢驗殘差的平穩(wěn)性,若平穩(wěn),則可認(rèn)為{yt}和{xt}間存在(1,1)階協(xié)整關(guān)系,即存在長期均衡,反之不存在。在存在協(xié)整關(guān)系的基礎(chǔ)上,引入誤差項建立誤差修正模型:
ecmt為誤差修正項。誤差修正模型既可描述變量的長期波動,又可通過差分項描述變量的短期波動,故該模型可研究變量的靜態(tài)(長期)趨勢和動態(tài)(短期)特征。
(三)Granger因果關(guān)系檢驗
即使判定兩變量間存在長期均衡關(guān)系,但是否存在因果關(guān)系,還需進一步檢驗。若變量x有助于預(yù)測y,即對y回歸時,加上x的滯后值可顯著提高回歸的解釋能力,則稱x為y的Granger原因,否則為非Granger原因。若x為y的Granger原因,說明x中包括了預(yù)測y的有效信息。其模型如下:
檢驗的零假設(shè)H0: a1=a2=…=aq=0,即x是y的非Granger原因。若零假設(shè)成立,則有:
用最小二乘法求出式(4)和式(5)的殘差平方和SSE1和SSE0,構(gòu)造自由度為(q,T-p-q-1)且服從F分布的統(tǒng)計量。其中,S為樣本容量,p為y的滯后階數(shù),q為x的滯后階數(shù),p和q用AIC準(zhǔn)則確定。比較F統(tǒng)計量與臨界值的大小,若F大于臨界值,則拒絕零假設(shè),即x為y的Granger原因,反之接受零假設(shè)。
三、實證研究
(一)樣本數(shù)據(jù)選擇和數(shù)據(jù)處理
本文以蘭州市為例,以1978-2013年財政收入(CZSR)和地區(qū)生產(chǎn)總值(GDP)為樣本數(shù)據(jù),所有數(shù)據(jù)均來源于《蘭州市統(tǒng)計年鑒》。
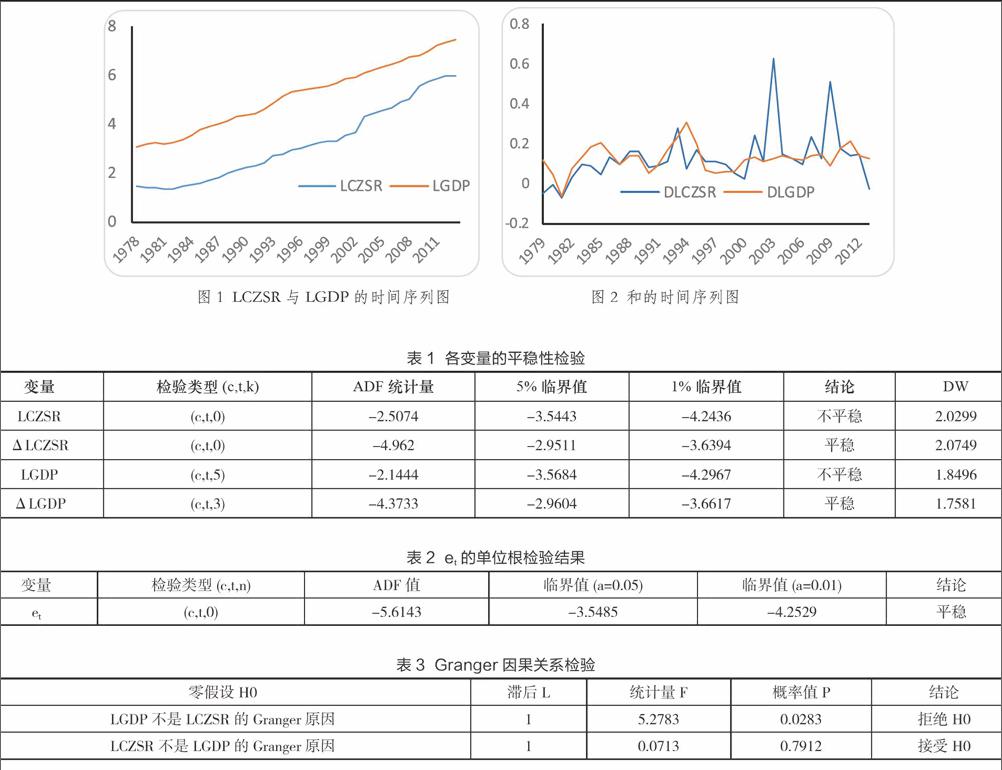
為消除數(shù)據(jù)中存在的異方差和趨勢線性化現(xiàn)象,在不改變變量間協(xié)整關(guān)系的前提下,首先對CZSR和GDP進行自然對數(shù)變換。變換后的財政收入和GDP分別用LCZSR和LGDP表示,其時間序列圖如圖1。從圖1可看出,LCZSR和LGDP都呈遞增趨勢,具有顯著的不平穩(wěn)性。故對LCZSR和LGDP進行一階差分,差分后分別用和表示,其時間序列圖如圖2。從圖2可看出,一階差分后的兩列時間序列均較平穩(wěn),可用單位根檢驗來證實其平穩(wěn)性。
(二)財政收入與GDP的單位根檢驗
進行ADF檢驗時,根據(jù)AIC準(zhǔn)則自動確定滯后階數(shù),檢驗結(jié)果見表1。從表1可看出,LCZSR和LGDP在5%和1%的顯著水平上都是非平穩(wěn)的;而其一階差分ΔLCZSR和ΔLGDP在5%和1%的顯著水平上都是平穩(wěn)的。由于LCZSR和LGDP經(jīng)過一階差分均變成平穩(wěn)序列,故LCZSR和LGDP都為一階單整序列,記為I(1)。
(三)財政收入與GDP間的協(xié)整檢驗和誤差修正模型
由單位根檢驗結(jié)果可知,LCZSR和LGDP均為一階單整序列,故二者可能存在協(xié)整關(guān)系。本文采用Engle Granger兩步法檢驗其協(xié)整關(guān)系。首先對LCZSR和LGDP進行協(xié)整回歸,其回歸方程為:
LCZSRt=-2.474321+1.0979LGDPt+ut(6)
R2=0.9582 A-R2=0.9570 F=779.6285 DW= 0.1902 S.E.=0.3175
由于協(xié)整回歸結(jié)果DW=0.1902較小,說明可能存在自相關(guān)。因此,需加入LCZSR和LGDP的滯后因素,并重新估計LCZSR和LGDP間的協(xié)整關(guān)系。利用AIC準(zhǔn)則確定LCZSR和LGDP的滯后階數(shù),得到如下模型:
LCZSRt=-0.4003+0.3441LGDPt-0.1737LGDPt-1+0.8772LCZSRt-1 +et(7)
R2=0.9942 A-R2=0.9937 F=1778.34 DW= 2.0175 S.E.=0.1213
現(xiàn)對et的平穩(wěn)性進行檢驗,結(jié)果如表2。由表2可知,ADF=-5.6143,5%的臨界值為-3.5485,1%的臨界值為-4.2529,因為ADF小于5%和1%的臨界值,所以在5%和1%的顯著水平上,et都是平穩(wěn)的,即et~I(0),因此,蘭州市財政收入與GDP間存在協(xié)整關(guān)系。其誤差修正項為:
ecmt-1=et=(LCZSRt+0.4003-0.3441LGDPt+0.1737LGDPt-1-0.8772LCZSRt-1)(8)
現(xiàn)將LCZSR與LGDP間的協(xié)整方程寫成如下形式:
LCZSR=α+βLGDP(9)
α=-0.4003/(1-0.8772)=-3.2598
β=(0.3441-0.1737)/(1-0.8772)=1.3876
故LCZSR與LGDP間的長期協(xié)整關(guān)系方程為:
LCZSR=-3.2598+1.3876LGDP(10)
根據(jù)協(xié)整關(guān)系方程,長期內(nèi),蘭州市(對數(shù))的生產(chǎn)總值每變動1%,同期(對數(shù))的財政收入將同方向變動1.3876%.
(四)財政收入與GDP的Granger因果關(guān)系檢驗
由于蘭州市對數(shù)的財政收入和對數(shù)的GDP均為一階單整且具有協(xié)整關(guān)系,故可檢驗二者的Granger因果關(guān)系,檢驗結(jié)果如表3:
根據(jù)格蘭杰因果關(guān)系分析可知,在滯后階數(shù)為1階顯著性水平為5%時,蘭州市GDP是蘭州市財政收入的Granger原因,而蘭州市財政收入不是蘭州市GDP的Granger原因,即蘭州市GDP是蘭州市財政收入的決定因素,而蘭州市財政收入不是蘭州市GDP的決定因素。因此,可用蘭州市GDP的變化來解釋蘭州市財政收入的變化,且蘭州市GDP的增加可以拉動蘭州市財政收入的增加。
四、結(jié)論
由協(xié)整檢驗可知,雖然蘭州市財政收入和蘭州市GDP均具有非平穩(wěn)性,但二者相關(guān)度較高,整體上存在長期穩(wěn)定的協(xié)整關(guān)系;由誤差修正模型可知,短期內(nèi)蘭州市財政收入和蘭州市GDP間的動態(tài)調(diào)整機制可使二者自動實現(xiàn)內(nèi)在的長期均衡。
由Granger因果檢驗可知,在滯后階數(shù)為1階時,蘭州市財政收入和蘭州市GDP間存在單向因果關(guān)系,即蘭州市GDP是蘭州市財政收入的Granger原因,而蘭州市財政收入不是蘭州市GDP的Granger原因。故蘭州市GDP的增長是蘭州市財政收入增長的決定因素,提高市內(nèi)經(jīng)濟發(fā)展水平能夠增加財政收入。
參考文獻:
[1]胡秀英.撫寧縣財政收入與GDP的相關(guān)分析[J].統(tǒng)計與管理,2015,(7):73-74.
[2]何凌云,胡振虎.我國財政收入超GDP增長的比較研究[J].財政研究,2013,(6):64-68.
[3]林國立,尚菲,張濤.蚌埠市GDP與財政收入增長關(guān)聯(lián)性分析[J].蚌埠學(xué)院學(xué)報,2015,4(3):179-183.
[4]王玉華,劉貝貝.山東省GDP與財政收入的實證分析[J].東岳論叢,2009,30(7):53-58.
[5]文秀琴.河南省財政收入與GDP相關(guān)性分析[J].河南財政稅務(wù)高等專科學(xué)校學(xué)報,2013,27(3):53-58.

