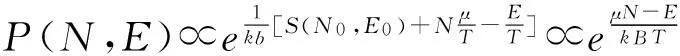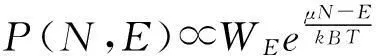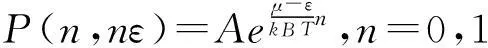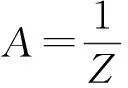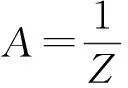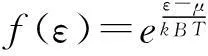關于近獨立子統計分布導出的探討
李建英
(忻州師范學院,山西忻州 034000)
?
關于近獨立子統計分布導出的探討
李建英
(忻州師范學院,山西忻州 034000)
[摘要]本文采用Darwin-Fowler平均法和Gibbs統計系綜理論,由熵和巨正則分布分別導出近獨立子的三種統計分布,克服了Boltzmann概率法在數學上人為假設的缺點,為三種統計分布的正確性提供了堅實的理論基礎。
[關鍵詞]玻色-愛因斯坦分布;費米-狄拉克分布;麥克斯韋-玻耳茲曼分布
任一宏觀量都是在一定宏觀條件下所有可能達到的微觀運動狀態的相應微觀量的統計平均值,在這一觀點的前提下,有不同的求統計平均值的方法,如Boltzmann的概率法、Darwin-Fowler的平均法、Gibbs的統計系綜理論.對于近獨立子的三種統計分布律導出,絕大部分教材采用Boltzmann的概率法,在導出過程中都假設ωi>>1,ni>>1,并使用了Stirling近似公式,實際上所作的假設未必能滿足,因此這是嚴重的缺陷,采用Darwin-Fowler的平均法和Gibbs的統計系綜理論導出所述的分布律則不存在數學上人為假設的缺點,為它們的正確性提供了堅實的理論基礎.
1用Gibbs的統計系綜理論,由巨正則分布導出近獨立子的三種統計分布
考慮全同近獨立子體系的巨正則系綜,其布函數為
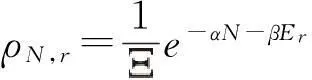
配分函數為

1.1Boss-Einstein分布律
玻色子的能級分布{ni}的總量子狀態數為
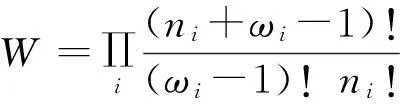
配分函數為
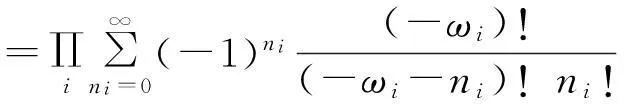
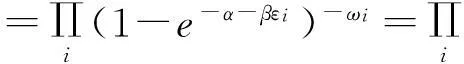

能級εi上的平均粒子數為
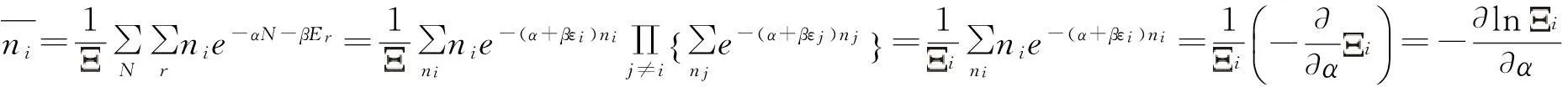

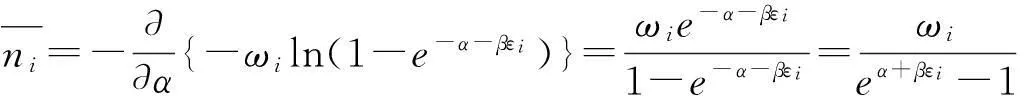
1.2Fermi-Dirac分布律
費米子遵守Pauli原理,ωi≥ni,能級分布{ni}的總量子狀態數為
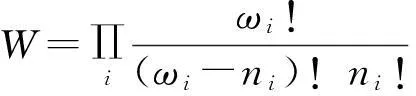
巨正則配分函數為

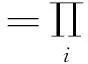

能級εi上的平均粒子數為
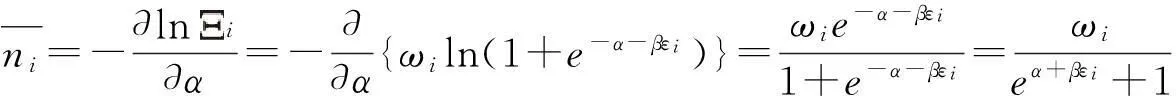
1.3Maxwell-Boltzmann分布律
離域獨立子經典體系,能級分布{ni}的總量子狀態數為
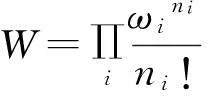
巨正則配分函數為

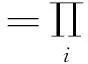

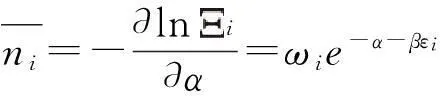
2用Darwin-Fowler的平均法,由熵引出三種統計分布
考慮一個具有恒定能量E0與恒定粒子數N0的很大的孤立系統,它由系統與其余很大的稱為媒質的部分構成,系統與媒質可以交換能量與粒子.當系統的能量為E,粒子數為N時,媒質的能量則為E0-E,粒子數為N0-N.當系統與媒質處于熱平衡時,兩者的溫度T與化學勢μ相等.
設系統對應于能量E的狀態數為WE,為一小量,因此系統與媒質所擁有的狀態數近似為媒質所擁有的狀態數,W(N0-N,E0-E),系統有N個粒子,能量為E的概率也就是媒質有N0-N個粒子,能量為E0-E的概率,這個概率和狀態數W(N0-N,E0-E)成正比,即P(N,E)∝W(N0-N,E0-E).
現用媒質的熵表示,則有
S(N0-N,E0-E)=kBlnW(N0-N,E0-E).
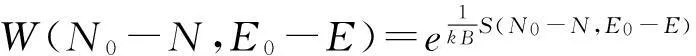
設N< 所以 若系統的能級E對應的狀態數WE≠1,則有 2.1Fermi-Dirac分布 現考慮由N個費米子構成的孤立系統,總能量為E,它由一個小系統與大媒質組成,取1個或0個費米子占據的單個量子態作為系統,取N個或N-1個費米子占據的其它量子態作為媒質.系統與媒質可以交換一個粒子和能量ε.由于費米子服從泡利原理,所以,對應的媒質所擁有的狀態數為W(N,E)或W(N-1,E-ε).熵為S(N,E)=kBlnW(N,E)或kBlnW(N-1,E-ε). 設系統的能量ε對應的狀態數WE=1,則系統有n個費米子,能量為nε的概率為 P(n,nε)∝W(N-n,E-nε). 或 2.2Boss-Einstein分布 現考慮玻色子系統,方法與費米子系統相同,差別在于對于費米子系統,n=0,1,而對玻色子系統,由于不受泡利原理制約,能量為ε的單個量子態允許有任意個玻色子占據,n=0,1,2,…. 設系統的能量ε對應的狀態數WE=1,則系統有n個玻色子,能量為nε的概率為 P(n,nε)∝W(N-n,E-nε). 或 2.3Maxwell-Boltzmann分布—經典情況 這是費米分布與玻色分布的共同極限情況,這就是經典的玻耳茲曼分布. 3討論 (1)用Darwin-Fowler的平均法,在數學方法上比概率法嚴格;另外,由熵引出三種統計分布,更突出了熵概念在統計物理中的重要地位,是對熵概念的進一步深化. (2)Gibbs的統計系綜理論,由巨正則分布導出近獨立子的三種統計分布,數學嚴謹,物理概念清晰,對獨立子體系與相依子體系都適用,是平衡態統計理論最完美的方法. [參考文獻] [1]高執棣,郭國霖.統計熱力學導論[M].北京:北京大學出版社,2004. [2]汪志誠.熱力學·統計物理[M].北京:高等教育出版社,2003. [3]嚴燕來,葉慶好.大學物理拓展與應用[M].北京:高等教育出版社,2002. [4]梁希俠,班士良.統計熱力學[M].呼和浩特:內蒙古大學出版社,2000. A Study on Derivating the Statistical Dstribution of Approximately Independent Partical LI Jian-ying (Xinzhou Teachers University, Xinzhou Shanxi 034000, China) Abstract:In the artical,statistical distributions of the appximately independent partical are derivated from entropy and grand canonical distribution through Darwin-Fowler statistical average and Gibbs statistical ensemble theory. It overcomes the shortcomings of Boltzmann probability statistics that gives the man-made assumption in mathematics and provids the solid theoretical basis for the correctness of three statistical distributions. Key words:Boss-Einstein distributions; Fermi-Dirac distributions; Maxwell-Boltzmann distributions [中圖分類號]O21 [文獻標識碼]A [文章編號]2095-7602(2016)04-0008-04 [作者簡介]李建英(1967- ),女,副教授,碩士,從事熱力學、統計物理和基礎物理實驗教學研究。 [基金項目]忻州師范學院基金項目“地方師范院校物理學專業實驗教學體系構建和創新人才培養模式研究”(JGZD201511)。 [收稿日期]2015-12-30