Forced Vibrations of a Submerged Finite Cylindrical Shell with an Internal Longitudinal Plate

,,,

(1.Wuxi Institute of Technology,Wuxi 214121,China;2.China Ship Scientific Research Center,Wuxi 214082,China;3.National Key Laboratory on Ship Vibration&Noise,Wuxi 214082,China)

Forced Vibrations of a Submerged Finite Cylindrical Shell with an Internal Longitudinal Plate

CUI Hong-fei1,QIAN Yan1,HUANG Jie1,YIN Xue-wen2,3

(1.Wuxi Institute of Technology,Wuxi 214121,China;2.China Ship Scientific Research Center,Wuxi 214082,China;3.National Key Laboratory on Ship Vibration&Noise,Wuxi 214082,China)

By utilizing Lagrangian equations,an approximation formulation is developed for the vibrations of a submerged finite cylindrical shell joined(hinged or clamped)to an internal longitudinal plate.The displacements for the cylindrical shell and its internal plate are respectively expanded as modal series while the displacement compatibilities at their junctions are enforced by Lagrange multiplier method.Fluid loading induced by the vibration of the shells is also taken into account,which is expressed in terms of the integral of harmonic Green’s function multiplied by boundary velocities over the vibrating surfaces.The numerical results for the natural frequencies and forced dynamic responses of shell structures agree well with the analytical solutions and FEM results, which demonstrates that the proposed method has great potential to address the dynamics of submerged finite cylindrical shell joined with an internal plate.

finite cylindrical shells;internal longitudinal plate;Lagrange multiplier

0 Introduction

Complex plate/shell structures are extensively used in many engineering applications, such as underwater vehicles,aircrafts,etc.,most of which can be generally modeled as the combinations of shells and/or plates,rings,frames,etc.The dynamic behaviors of the empty plate/shell structures are often modified by the addition of their internal structures due to the mechanical coupling between them at their interfaces[1-2].Reddy and Mallik[3]studied an infinite cylinder stiffened with axial frames,in which case the circumferential harmonics are coupled,but effects of axial stiffeners on the sound radiation were not addressed.A series of papers by Guo[4-7]gave good insights into the mechanism of the scattering and radiation from an infinite cylindrical shell due to the presence of the internal plate.In particular,Guo[7]examined the effects of four types of joints at two connected flat plates,namely,fully clamped attachment and pinned joints,on the sound scattering.It was shown that the scattered field is dominated by contributions from normal forces.Skelton[8]proposed a 3×3 receptance matrix involving simultaneously axial and circumferential co-ordinates,for an infinite cylindrical with an axial line force.

The above works utilized either wave approach or its alternatives,through which the responses of the shell were decomposed into free waves within it.When the shell is in finite length,the waves often manifest themselves in the form of modes with particular frequencies[9], and sound radiation is then associated with structural modes.In this case,modal approach is an effective and alternative way,through which the displacements can be represented as mode expansions or other series,such as trigonometric functions,power series,etc.Therefore,conventional approximate approaches such as Rayleigh-Ritz method,Galerkin method,or finite element method,etc,can be readily implemented.One of the earliest papers involving this subject may be traced back to Junger[10]who used the Lagrange equations to investigate a submerged,infinite shell reinforced with regularly spaced rigid septa and stiffening rings.Due to the rigid septa,the Fourier series expanded in a finite shell was used in deriving the dynamic equations of such an infinite shell.The elastic stiffeners were taken into account in terms of the prescribed shell displacements,which may correspond to the additional mass and stiffness in the governing equations of the shell.Besides,the fluid loading due to the acoustic field is divided into the contribution from the acoustic reactance and resistance,which,respectively, represent the added mass and radiation damping.Using Lagrange equations,several researchers addressed the vibrations of cylindrical shells with oddly-stiffened rings[11]and longitudinal stiffeners[12].

The dynamics of rings or frames are usually simplified as one dimensional problem,so their displacements can be readily represented in terms of those of the shells[10-12].The governing equations of the combined system can be directly expressed through the generalized coordinates of the shell.When the shell is connected to the plate,the dynamic behaviour of the plate is generally two-dimensional.Moreover,the generalized co-ordinates of the plate and the shell are not independent and the displacement compatibility between them must be enforced. Peterson and Boyd[13]investigated the free vibration of a finite cylinder with a longitudinal plate,where the combination of beam functions and circumferential mode series is prescribed. Bjarnason et al[9]investigated the sound radiation from a cylindrical shell with a flat plate and various types of connections between the plate and the shell were also considered.They all enforced the coupling conditions by introducing the Lagrange multipliers.Another way to deal with this problem was proposed by Missaoui et al[14]who modeled the mechanical coupling between the plate and the shell through an artificial spring.

Besides,when the shells are submerged in unbounded acoustic medium,the fluid-shell interaction must be taken into account.For infinite cylindrical shells,analytical expression for the acoustic field generated by the vibrating cylindrical surface is readily expanded as double series in cylindrical co-ordinates[1-4].However,it is awkward to deal with the fluid-shell interaction for a finite length shell due to the discontinuity of the surface velocity beyond its two ends.In this case,we have to resort to the classical surface integral formulation which is available for vibrating surface with arbitrary configuration[15].For the exterior problem for Neumann boundary condition,Stepanishen[16-17]proposed the acoustic impedance expressions for a finitevibrating cylindrical surface in terms of the shell’s in vacuo eigenfunctions,considering the effects of self-and interaction radiation impedance.In the present paper,the governing equations of for the vibrations of a submerged finite cylinder with an internal plate will be developed.The displacement compatibility along plate-shell conjunctions is enforced by the method of Lagrange multiplier.Numerical examples are also provided,which is partially validated by numerical method,as well as analytical method.

1 Model description and theory

1.1 Dynamic equations of the plate and the shell

Consider a thin cylindrical shell with a flat plate hinged or clamped to it along its axial direction as shown in Fig.1.The shell and the plate are both with finite length of l and their two ends are simply supported.The radius of the shell is given by a and thickness by hs,and the thickness of the plate is given by hp.The shell is immersed in an acoustic medium with density ρ0and sound velocity c0.Fluid loading inside the shell is assumed to be negligible.The two ends of the shell are connected to the rigid circular extensions.The plate is driven with a harmonic force vectorand the shell is driven by a harmonic force vector.For simplicity,it is assumed that all the loadings have the time dependence ofwhere ω is the angular frequency and t is the time. For algebraic convenience,will henceforth be suppressed throughout.

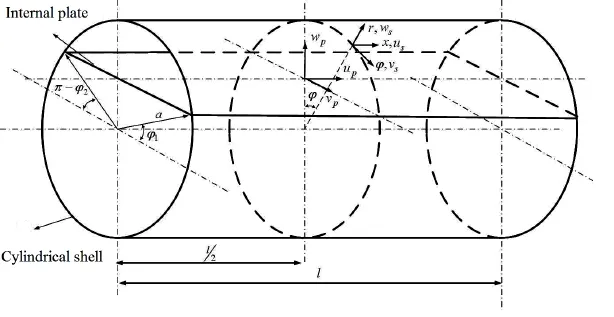
Fig.1 Illustration of an finite cylindrical shell connected with an internal plate

The displacement functions of the shell can be expanded as assumed series in φ and xaxes

where us,vs,and wsare the longitudinal,circumferential and radial displacements of the shell, respectively.Umn,Vmnand Wmnare the undetermined amplitude coefficients.

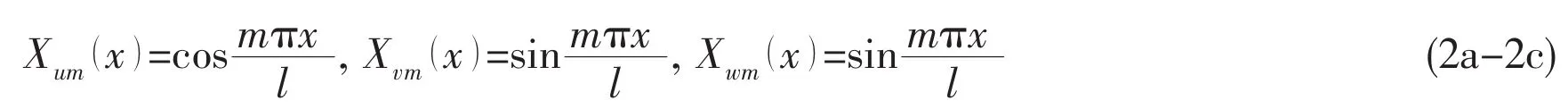
The circumferential functions that are used for the shell are given as follows,for symmetric modes,

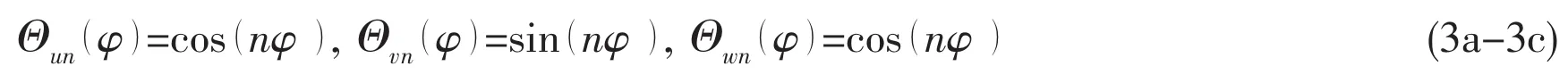
and,for antisymmeric modes

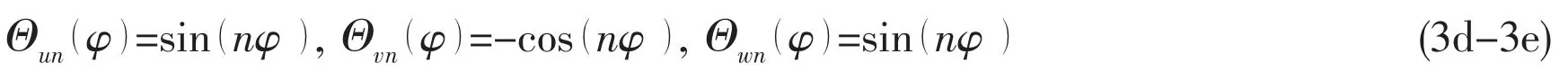
Eq.(1)may be written in a concise matrix form as follows:

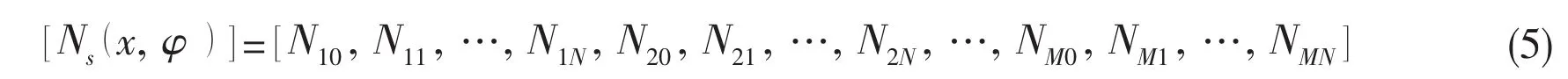
where the sub-matrix in Eq.(5)is

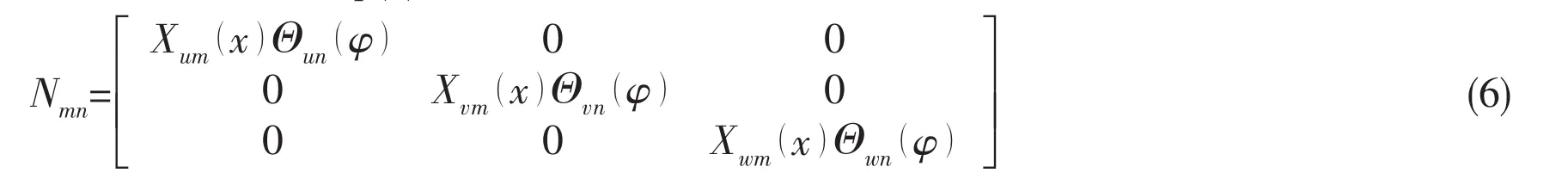
The generalized displacement vectoris arranged in the following form:

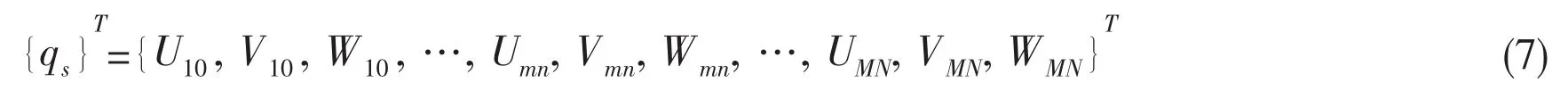
Similarly,the displacements for the plate may be expressed as follows:

and are written in a concise matrix form

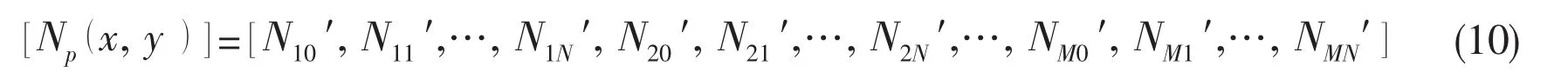
and the corresponding sub-matrix is

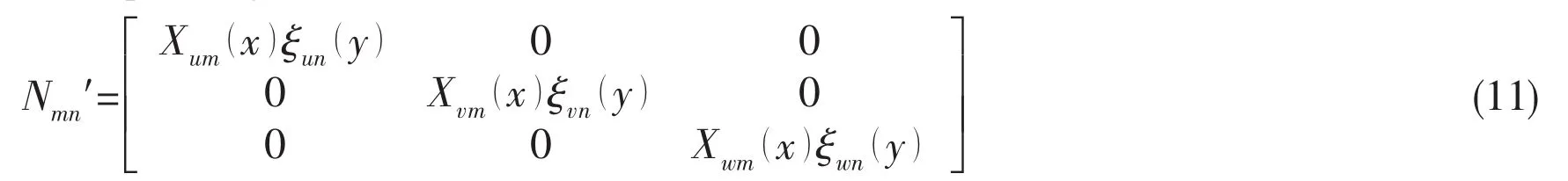
According to thin shell theory,the kinetic energy of the shell associated with us,vsand wsis

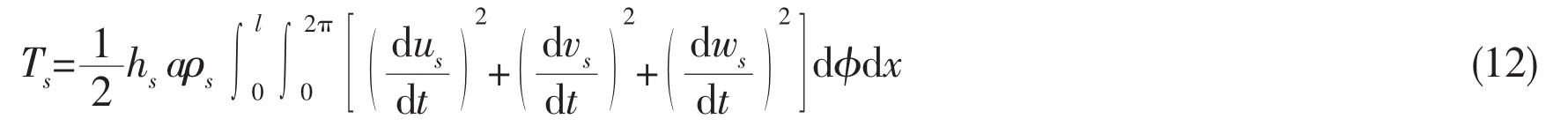
and the strain energy of the shell in its middle surface is

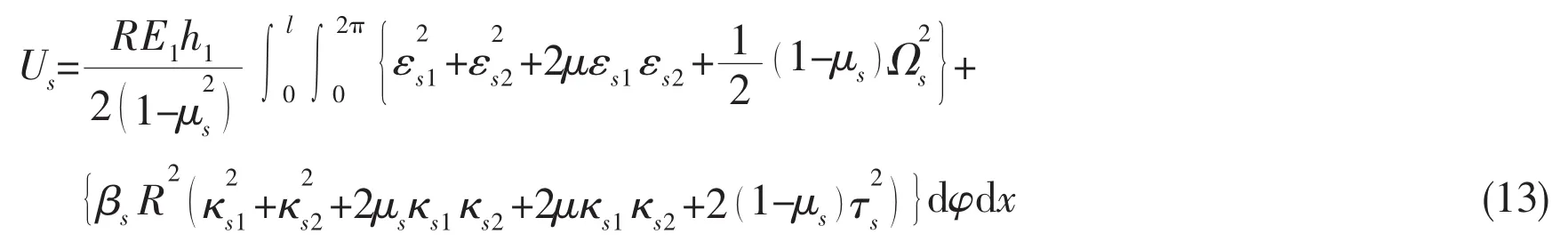
Similarly,the kinetic energy of the internal plate is

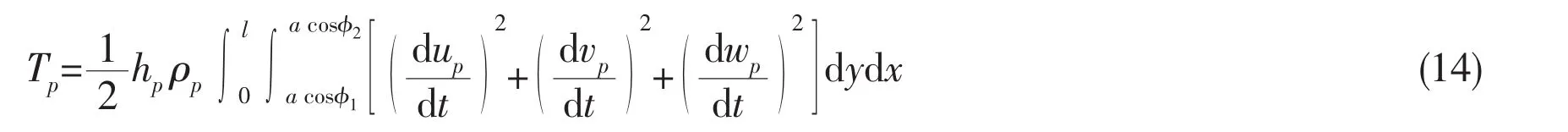
and the strain energy of the plate is

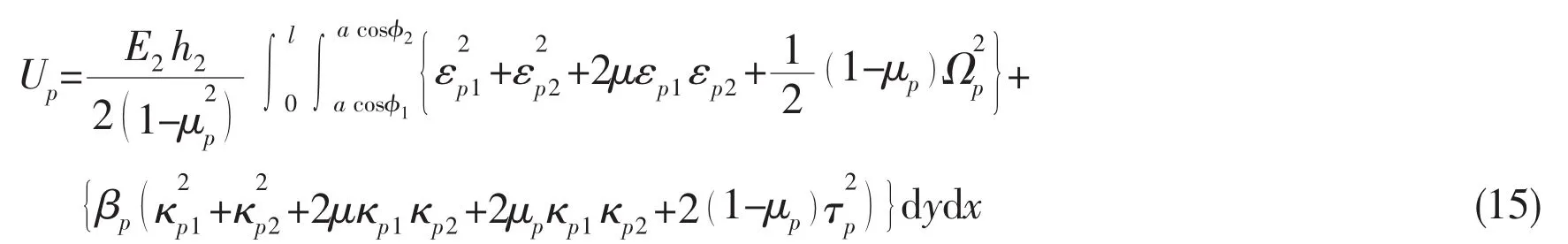
where βsand βpare geometric parameters of the shell and plate,respectively.The strain formulations in the thin plate and shell theory are as follows:

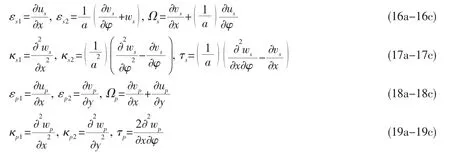
The kinetic and strain energies of the shell and plate are respectively written in the following matrix form:

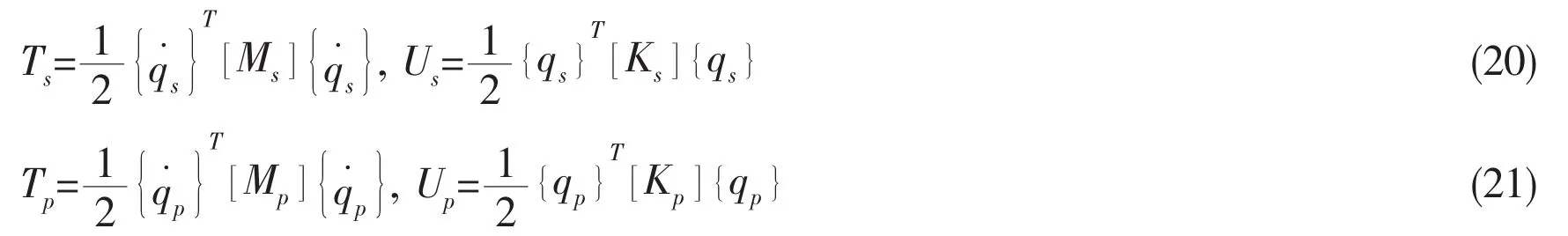
The work done by the external force at the internal plate is

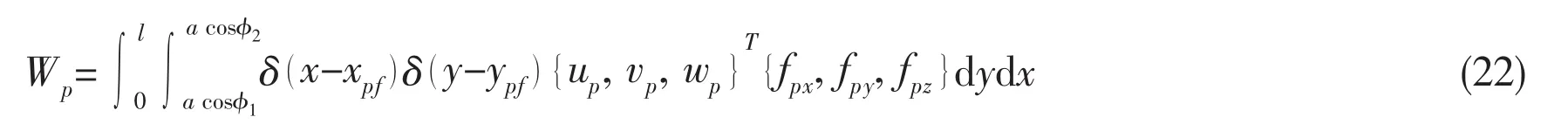
substituting Eq.(9)into Eq.(22),yields

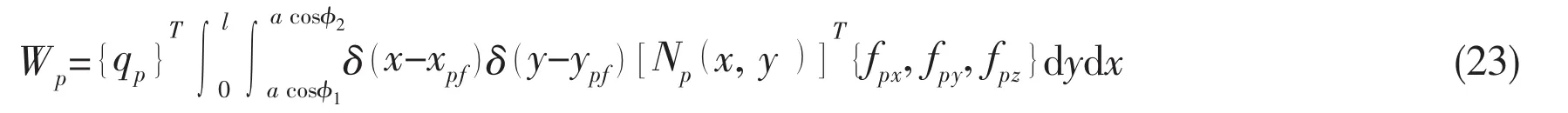
Eq.(23)may be written in the matrix form as follows:

Similarly,the work done by the external force at the shell is

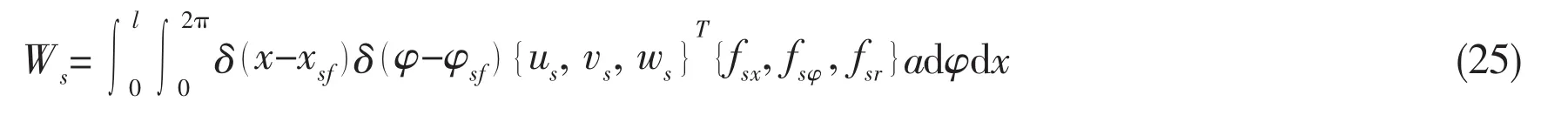
substituting Eq.(4)into Eq.(25),yields

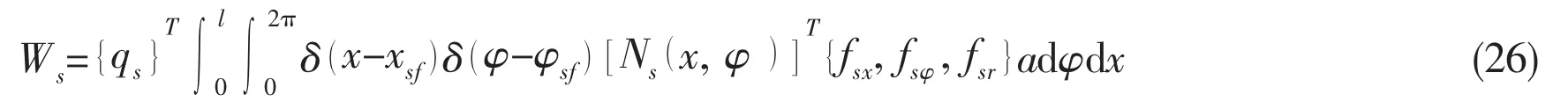
Eq.(26)may be written in the matrix form as follows:

1.2 Displacement compatibility between the plate and the shell

When the plate is connected,e.g.clamped or hinged,to the shell along their junctions, compatibility of displacements and rotations between the plate and the shell is required.For the clamped attachment,all three displacements and rotations of the shell must be equal to those of the plate,which can be satisfied by enforcing the following conditions:

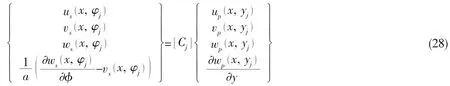
Substituting Eq.(4)and Eq.(9)into Eq.(28),displacement capabilities can be further expressed by the following expression:

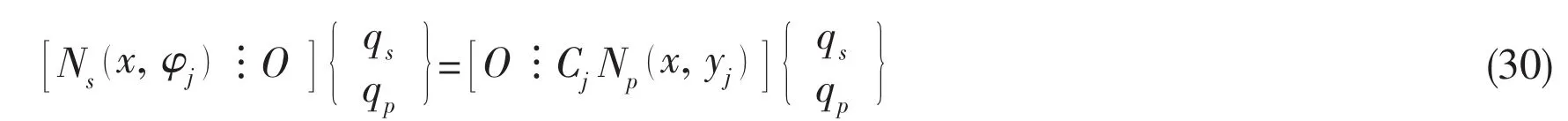
Transposing the right terms of Eq.(30)to the left side and gathering them up

The constraint equations at the two junctions between the plate and the shell can be expressed as follows after the transpose of the matrix:

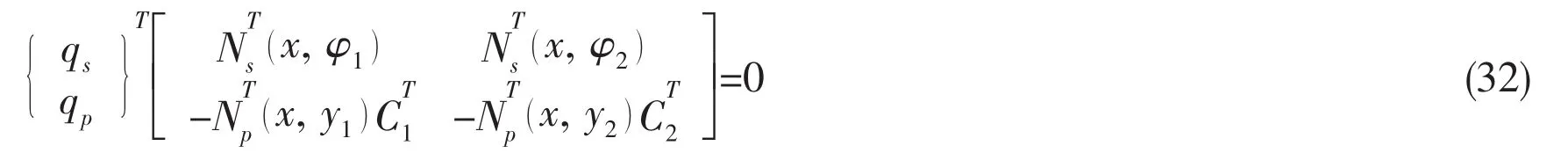
1.3 Work done by the acoustic field

For vibrating surfaces,the exterior acoustic pressure is simply expressed as the wellknown surface integral

When the radial velocity of the shell is assumed as follows:

the harmonic Green’s functionfor exterior Neumann boundary value problem can be expressed as

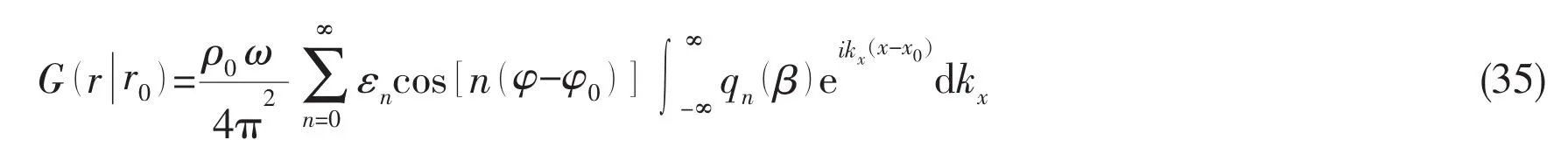
The work done by the acoustic field could be expressed as follows:

Substituting Eqs.(4)and(33)into Eq.(36)yields

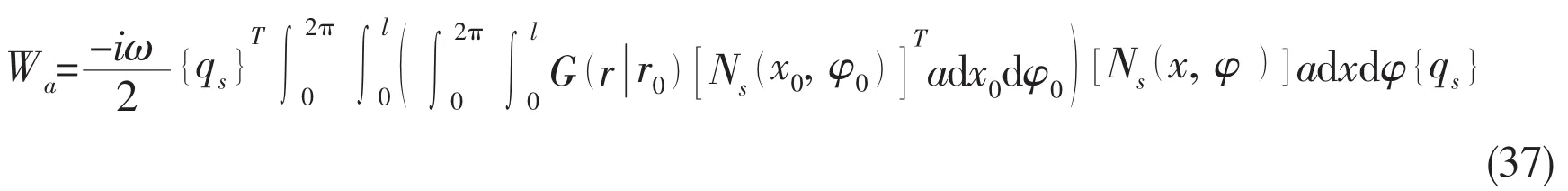
The work done onto the shell by the acoustic field may be written in the following matrix form:

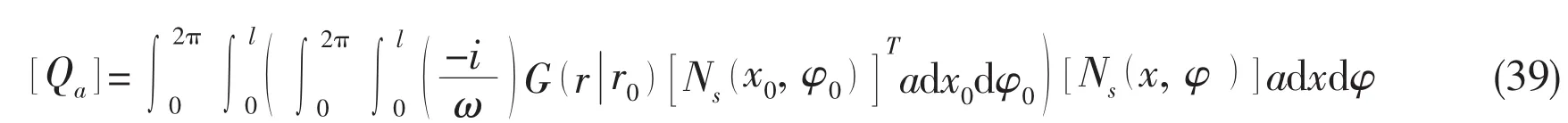
Eq.(39)is very complex,and when Stepanishen’s method[16]is employed,it reduces to the following more concise form

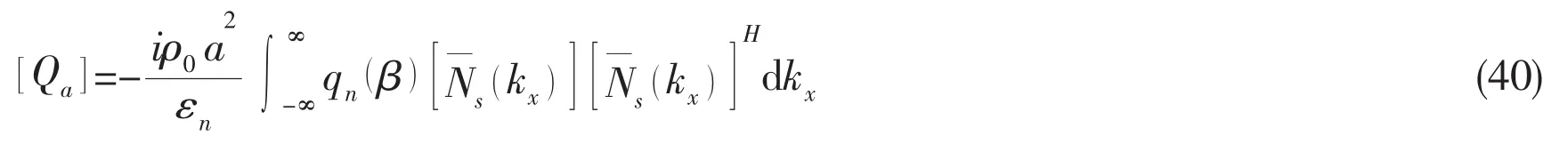
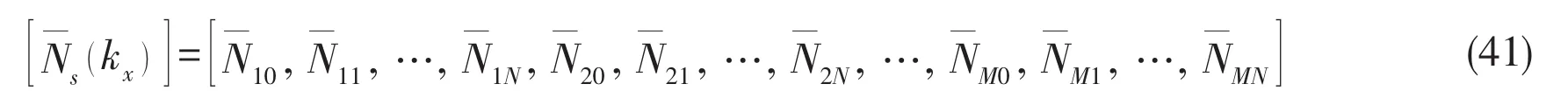
where the sub-matrix in Eq.(41)is

1.4 Governing equations in terms of generalized co-ordinates

In the above sections,the kinetic and potential energies of the shell and plate are ex pressed in terms of the generalized co-ordinates by using the stain-displacement relations and the material constitutive relations.The components of the co-ordinate vectors of the shell and plate are not independent because constraint equations must be introduced to ensure displacement compatibility along the junctions between the plate and the shell.Thus the modified Lagrangian is employed by adjoining the constraint equations through a vector of Lagrange multipliers,

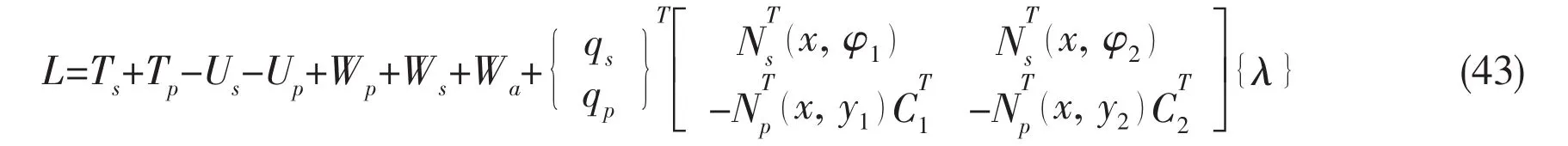
The whole system is characterized by using the classical Hamilton’s principle,which needs the calculations of the kinetic and strain energy of the combined system,as well as the work done by the external force and induced acoustic pressure.The modified Lagrangian is then substituted into Lagrange’s equations as follows:

then the following governing equations in a matrix form are obtained:

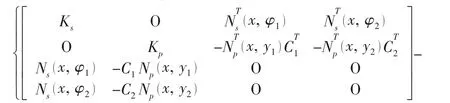
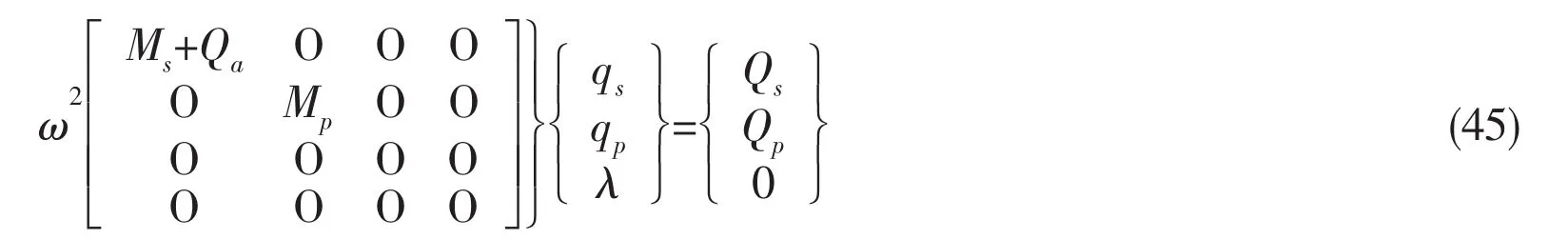
Eq.(45)is a standard linear equation,however,are not positively definite matrices because when the index number n is zero,as shown in Eqs.(1)and(8),all elements in the corresponding rows and columns ofare zero,which shall be eliminated before numerical implementation.

When the external forces at the shell and the plate are omitted,Eq.(45)will reduce to the eigenvalue problem of a fluid-loaded finite cylindrical shell,particularly,when the fluid loading termis also ignored,Eq.(45)will further reduce to the eigenvalue problem of a‘dry’ finite cylindrical shell.

2 Numerical examples and validation

2.1 Resonant modes of the finite shell

When the fluid-loaded shell is loaded without any internals,Eq.(45)will reduce to the following,

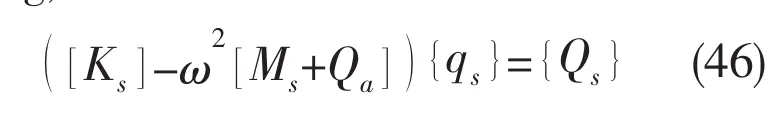
Particularly,when the fluid loading termand the external force vectorare omitted,Eq.(46)will reduce to the eigenvalue problem for a‘dry’finite cylindrical shell.In this section,the natural frequencies of a simply supported finite cylindrical shell without fluid loading are solved by the present method as well as by the analytical method. The parameters of shell are given in Tab.1.

As shown in Tab.2(a)-Tab.2(d),the vibration modes calculated by the present method agree well with those obtained by the analytical method.

Tab.1 Parameters of the finite cylindrical shell(SI units)

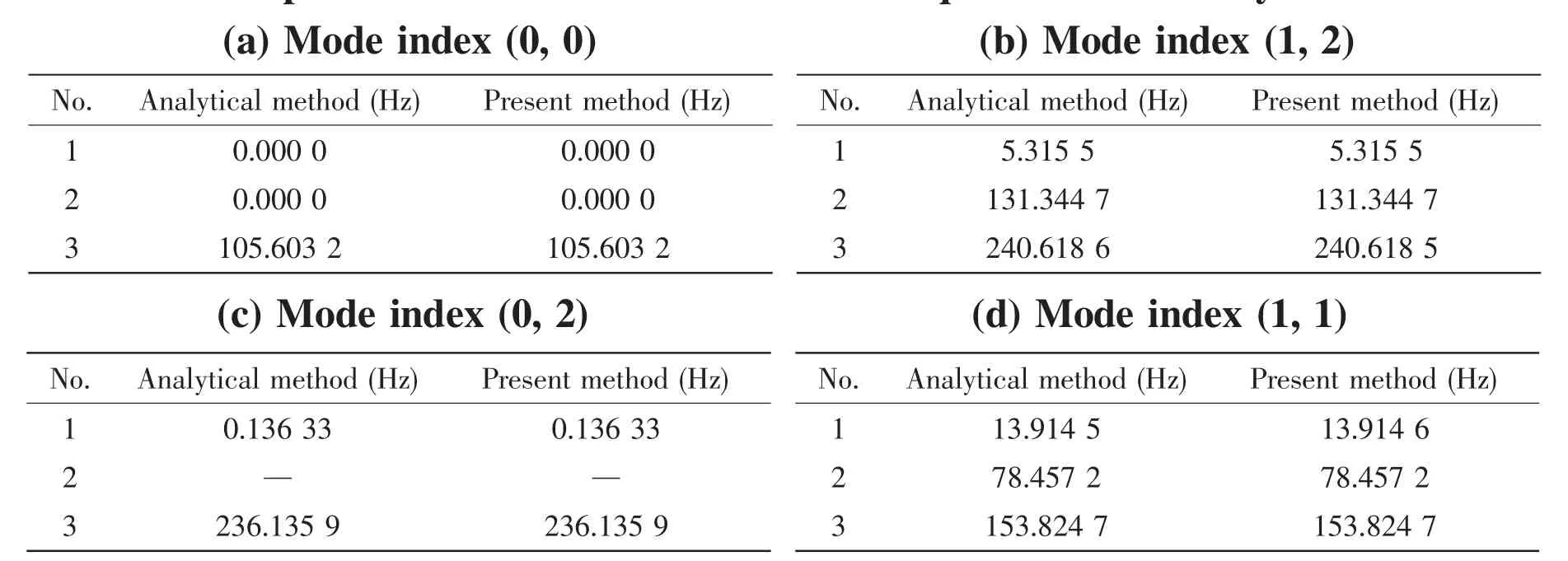
Tab.2 Comparison of our obtained resonant frequencies with analytical results:

2.2 Forced responses of the finite shell with internal plate

The parameters of a finite cylindrical shell rigidly connected with an internal plate are shown in Tab.3.The eigenvalue problem of such a model is solved by ANSYS and by the present method,respectively.Once the eigen vectors qs｛ ｝and qp｛ ｝are determined from the eigenvalue problem of Eq.(46),the modal shapes of the shell-plate structure may be obtained from Eqs.(4)and(9).

Tab.3 Parameters of the finite cylindrical shell rigidly connected with an internal plate(SI units)

The internal plate is driven by a harmonic point force and the response point is chosen at the shell,the locations of which are listed in Tab.3.As shown in Fig.2,when the shell is hinged with an internal plate,the responses at the given point obtained by FEM and by the present method agree well.Similarly,in Fig.3,when the shell is rigidly connected with an internal plate,the responses at the same point by the two methods also agree very well.

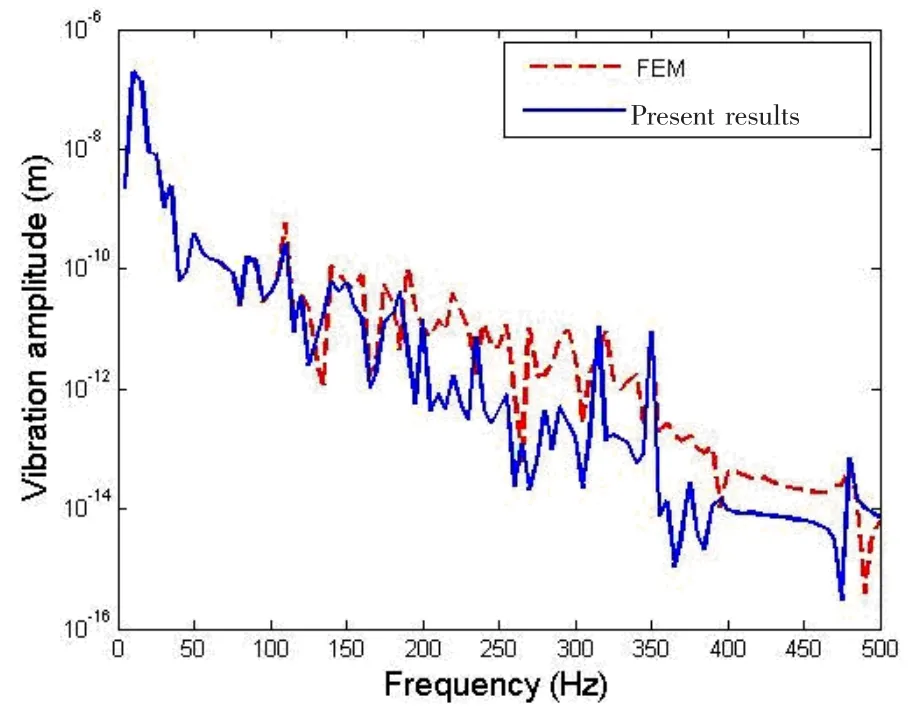
Fig.2 Comparison of forced responses of a simply supported cylindrical shell hinged with an internal plate with FEM results

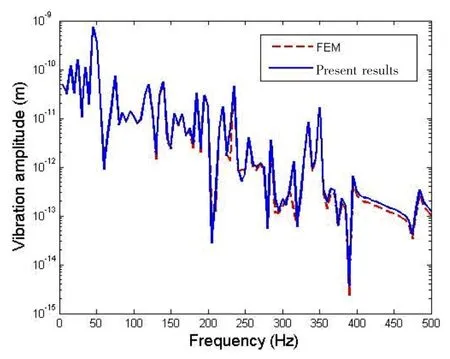
Fig.3 Comparison of forced responses of a simply supported cylindrical shell rigidly connected with an internal plate with FEM results

3 Conclusions

Though this work needs further validation through experiments or related results,thederivation process of the governing equations and its numerical implementation are well selfcontained.In addition,compared to conventional FEM,this method has great computation efficiency because of inherent minimum discretization requirements,especially in high frequencies.

Hence,we can conclude that our method has great potentials in dealing with the vibrations of combined plate-shell structures due to its high computation efficiency and accuracy. We can also anticipate that this method can be facilitated in addressing the dynamic characteristics of internal plate structures and the supporting shells.

[1]Yin X W,Liu L J,Hua H X.Acoustic radiation from an infinite laminated composite cylindrical shell with doubly periodic rings[J].J of Vibration and Acoustics,2009,131:011005-1.

[2]Li Guang,Wu Wenwei.Vibration and sound radiation research based on power flow method[J].Journal of Ship Mechanics,2015,19(5):609-618.(in Chinese)

[3]Reddy E S,Mallik A K.Response of and sound radiation from a layered cylinder with regular axial stiffeners[J].J Sound and Vibration,1985,103(4):519-531.

[4]Guo Y P.Acoustic radiation from cylindrical shells due to internal forcing[J].J Acoust.Soc.Am.,1996,99(3):1495-1505.

[5]Guo Y P.Acoustic scattering from cylindrical shells with deck-type internal plate at oblique incidence[J].J Acoust.Soc. Am.,1996,99(5):2701-2713.

[6]Guo Y P.Acoustic scattering by bulkheads in cylindrical shells[J].J Acoust.Soc.Am.,1993,93(4):1936-1946.

[7]Guo Y P.Effects of structural joints on sound scattering[J].J Acoust.Soc.Am.,1993,93(2):857-863.

[8]Skelton E A.Line force receptance of an elastic cylindrical shell with heavy exterior fluid loading[J].J Sound and Vibration,2002,256(1):131-153.

[9]Bjarnason J,Achenbach J D,Igusa T.Acoustic radiation from a cylindrical shell with an internal plate[J].Wave Motion, 1992,15:23-41.

[10]Junger M C.Dynamic behavior of reinforced cylindrical shells in a vacuum and in a fluid[J].J App.Mech.,1954,3:35-41.

[11]Basdeks N,Chi M.Response of oddly stiffened circular cylindrical shells[J].J Sound and Vibration,1971,17(2):187-206.

[12]Rinehart S A,Wang J T.Vibration of simply supported cylindrical shells with longitudinal stiffeners[J].J Sound and Vibration,1972,24(2):151-163.

[13]Peterson M R,Boyd D E.Free vibrations of circular cylinders with longitudinal,interior partitions[J].J Sound and Vibration,1978,60:45-62.

[14]Missaoui J,Cheng L,Richard M J.Free and forced vibration of a cylindrical shell with a floor partition[J].J Sound and Vibration,1996,190(1):21-40.

[15]Sandman B E.Fluid-loading coefficients for a finite cylindrical shell[J].J Acoust.Soc.Am.,1976,60(6):1256-1264.

[16]Stepanishen P R.Modal coupling in the vibration of fluid-loaded cylindrical shells[J].J Acoust.Soc.Am.,1982,71(4): 813-823.

[17]Stepanishen P R.Radiated power and radiation loading of cylindrical surfaces with nonuniform velocity distributions[J].J Acoust.Soc.Am.,1978,63(2):328-338.

具有內部縱板的水下有限圓柱殼體的強迫振動

崔宏飛1，錢 燕1，黃 捷1，殷學文2，3

（1.無錫職業技術學院，江蘇 無錫214121；2.中國船舶科學研究中心，江蘇 無錫214082；3.船舶振動噪聲國家重點實驗室，江蘇 無錫 214082）

運用拉格朗日方程，導出具有內部縱板鉸接或固接的水下有限圓柱殼體的振動方程。平板和圓柱殼體的位移場皆采用假設振型展開形式，而殼體和平板之間的位移連續條件通過引入拉格朗日乘子法實現。殼體振動誘發的流體負載采用格林函數和邊界振速乘積的邊界積分方程表示。采用文中方法得到的殼體結構自然頻率和強迫響應同解析法、有限元結果符合良好，表明該方法對于處理具有內部平板結構的有限圓柱殼體的動力學問題有較好適用性和較大潛力。

有限圓柱殼；內部縱板；拉格朗日乘子

O326

A

崔宏飛（1975-），女，無錫職業技術學院講師；

O326

A

10.3969/j.issn.1007-7294.2016.06.009

1007-7294（2016）06-0736-12

錢 燕（1981-），女，無錫職業技術學院講師；

黃 捷（1963-），女，無錫職業技術學院副教授；

殷學文（1974-），男，博士，中國船舶科學研究中心高級工程師。

Received date：2016-03-05

Biography:CUI Hong-fei(1975-),female,lecturer of Wuxi Institute of Technology;QIAN Yan(1981-), female,lecturer of Wuxi Institute of Technology;YIN Xue-wen(1974-),male,correspondence author,senior engineer of CSSRC.