巧用輔助線解決問題
王瀚
最近,剛學完用反比例函數解決問題,我就在課后獨自做了幾個練習來試試手. 剛開始的幾道題做起來得心應手,心里便有些沾沾自喜,但是繼續往下做的時候,這個節奏就被打斷了,因為下面這道題我不知道該如何下手了.
如圖1,E為矩形ABCD的邊CD上的一個動點,BF⊥AE于F,AB=3,BC=4,設AE=x,BF=y,求y與x之間的關系式,并寫出x的取值范圍.
首先我可以確定的是,點E在CD上運動,那么AE最短時長度與AD相等,AE最長時長度與AC相等,根據勾股定理,我可以得到AC=5,所以我可以確定x的取值范圍是3≤x≤5,但是還要求y與x的關系,這可把我難倒了. AE和BF就是兩條互相垂直的線,怎么才能確定它們之間的關系呢?
想來想去,還是直接去問老師吧. 老師看了一遍題目,說道:“BF和AE垂直,想想垂直有什么用呢?”我又想了一會,搖搖頭,感覺這個垂直好像還是沒法用.
這時老師把BE連接起來:“再看看這個垂直,現在有什么用呢?”我頓時眼前一亮:“我看到了直角三角形BFE.”當我正激動時,老師卻說道:“直角三角形BFE中BF有了,可是EF不知道呀,我們想要的是BF和AE之間的聯系呀,你再看看,BF和AE這個垂直怎么可以為你所用?”這時,我又仔細地思考了一遍,發現這個垂直可以把AE作為底,BF看做是底邊上的高,用來求三角形的面積. 而且這個三角形的面積還可以通過另外一種方法來求:把AB看做是底,那這個三角形的高就等于BC的長度. 這樣之后得到關于x和y的關系式:1/2xy=1/2×3×4,化簡之后得到y=12/x,再考慮之前x的取值范圍,那這道題的最后結果應該是:y=12/x(3≤x≤5).
一想到我想了好久的題目,老師畫了一條輔助線之后很快就解決了,我頓時感覺輔助線真的很神奇,可以化復雜為簡單. 而我以后碰到這種圖形的問題,在沒有思路的時候也可以換條途徑,想想能不能添加輔助線來幫助解決問題.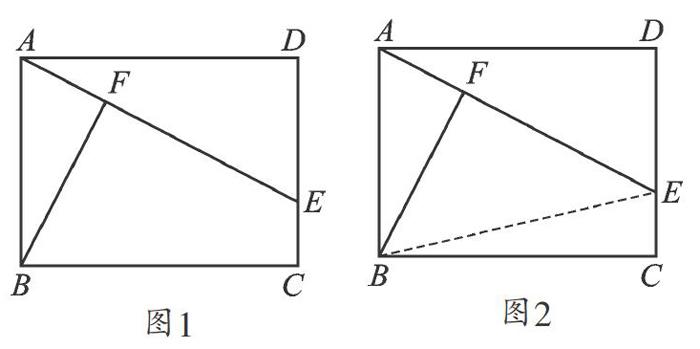
教師點評:該生能敏銳地察覺到x的取值范圍實屬不易,而且知道想要利用垂直解題,但是找不到突破口. 在這道題中,利用好這個垂直是解決本題的關鍵,這時候要想到垂直就有垂線段,聯想到三角形的面積也需要垂線段,那就構造一個三角形,建立x和y所對應的兩條邊之間的聯系,這時候這個問題就迎刃而解了.
(指導教師:龔 瑩)

