超密集網絡中寬帶頻譜快速感知研究

周雄

為滿足超密集網絡中基站對寬帶頻譜資源的實時感知要求，提出了一種寬帶頻譜感知算法。本方法根據信號結構，通過保護邊帶獲得噪聲功率水平，據此迭代獲得平均信號功率，從而得到信號與噪聲的最佳判決門限，感知空閑頻譜。本方法運算復雜度低，適用于已知信號結構下的寬帶頻譜感知。仿真結果表明，該算法有較好的性能且能適應較低信噪比的條件。

超密集網絡 寬帶頻譜感知 快速感知

1 引言

超密集網絡通過提高接入點密度，提高了區域頻譜效率，是5G通信的重要發展方向。在超密集網絡中，基站與認知無線電的結合將提升站點的即插即用能力[1]，提供高速率、低耗能的通信服務。

頻譜感知作為認知無線電技術的核心功能，受到了廣泛的關注，主要的頻譜檢測方法有：能量檢測[2-3]、匹配濾波檢測[4]、特征檢測[5]以及波形檢測[6]等。然而對于超密集網絡，同一資源可能被多個相鄰站點使用，感知信號復雜。感知基站通常處于鄰居站點有效覆蓋范圍之外，信噪比條件較差，為保證負載的實時通信，須在較短感知周期內完成感知。對于寬帶頻譜感知方法，目前的研究成果主要是最優化頻譜檢測方法[7]，但是其感知周期長、復雜度高、可操作性低，其判決門限獲取方法復雜，在超密集網絡中不可行。在自組織網絡中，由于感知信息難以相互共享，多個感知節點聯合檢測方法[8]難以在此適用。當前對于超密集網絡中需要的，快速、準確、低復雜度的寬帶頻譜感知技術仍需進一步研究。

本文提出了一種寬帶頻譜檢測技術，通過前端采樣的子頻帶信息，利用保護邊帶的噪聲信息，估計噪聲功率與信噪比，從而獲得最佳判決門限。在一個符號周期內，只需一次FFT運算，快速有效地得到感知帶寬內各子頻段的使用情況。本文方法利用保護邊帶的噪聲信息，獲得了最佳判決門限，復雜度低、可行性高、實時性能好，適合超密集網絡中實際需要的寬帶頻譜感知。

2 系統模型

2.1 無線感知環境

在自組織的超密集網絡中，各基站之間競爭共存，其配置參數一般各不相同，具體如圖1所示。為滿足用戶的需求，保證網絡中頻譜資源能夠被各個基站最優化地分配使用，每一個基站都必須實時掌握自己覆蓋范圍內的可用頻譜資源信息，從而選擇最佳頻譜使用策略。所以，網絡中的每一個基站都需要對寬帶頻譜中各個子頻帶進行感知，需要實時地、高效地感知出寬帶頻譜內每一個頻點的使用情況。并且通常感知基站不在鄰居節點覆蓋范圍內，信噪比條件較差，因此感知方法還需在低信噪比條件下有較好的性能。

對于頻分復用的無線通信方式，其頻譜都包含一個特定的工作頻段和相應的保護頻帶。工作頻段會被劃分為多個通信子頻帶，每個子頻帶會占據一定帶寬，保護頻帶則沒有被任何用戶使用。例如在LTE寬帶通信中，頻帶寬達20MHz，等間隔劃分為110個資源塊，每個資源塊包含12個子載波。此外，有寬達數十兆赫茲的保護頻帶。

2.2 感知信號

在LTE系統中，頻譜資源的分配是以資源塊為單位的。以一個資源塊為單位進行分析，既能滿足頻譜感知精細度的要求，又能避免信號畸變對OFDM信號正交性破壞帶來的影響。綜上所述，感知需求就是正確感知每一單位頻率資源的使用情況。

在自組織超密集網絡中，各站點可自由加入或退出頻移資源共享系統的，在感知周期內，站點之間缺乏協調機制。所以，基站接收到的信號往往來自多個基站，令接收信號xmi（t）代表來自編號為m的鄰居節點第i段頻譜時域檢測信號，則：

其中smi（t）表示發送信號，vmi（t）表示時域噪聲，M表示鄰居基站個數，H0代表沒有信號，H1代表有信號。令I表示感知寬帶內的頻譜單元總數，αi，m為相應信道增益，那么總的寬帶范圍的接收信號就為：

3 寬帶頻譜感知方法

超密集網絡中，通常感知信號是來自多個站點信號的疊加，這會使得感知信號特征被破壞。對于某一頻段，選擇能量感知來判斷是否被占用是一種簡單的方法。對于本文討論的場景中全體子頻帶的感知，因為空口信號的結構是已知的，因此可以確定保護帶的位置，保護帶不會被任何站點所使用。因此，可以利用這一先驗知識，獲得噪聲功率的電平值，通過迭代運算，計算出平均信號功率，從而得到最佳判決門限。對所有子載波是否被占用進行最終判決，具體流程如圖2所示：

下文中，詳細分析了從前端采樣獲得的時域信號，并推導出最佳判決門限，詳細敘述了迭代獲取平均信號功率的方法，估計出信噪比參數，完成了寬帶頻譜的感知。

3.1 寬帶采樣信號分析

對于感知節點而言，若有任意一個鄰居節點正在使用某一子頻段，則感知基站應避免使用該子頻段，令xi（t）為子頻段i的總感知信號，則有：

令Ei（x）表示子頻段i對應的時域感知信號能量，ωi表示某頻點或者該資源塊所對應的頻率范圍的中心頻率，△ω表示對應頻率單元的頻譜寬度，Tsense為感知周期，F（ω）為感知信號的傅立葉變換。則由帕塞瓦爾定理可知：

可令Tsense=N×Tsample，其中Tsample為基站的信號采樣周期，N則為感知周期內的采樣點數。令為感知信號N點離散傅立葉變換值，于是感知能量估計值為：

其中，服從卡方分布[9]，但是當N足夠大時（一般只需N≥20，在實際通信系統中很容易滿足），可以認為漸進的服從正態分布，其統計特征模型如下：

其中Ps為信號功率，δ2v為噪聲功率。當選擇一個判決門限γ之后，相應的虛警率與檢測率分別可表示為：

若是采用FFT運算進行功率譜估計，則在一個感知周期內就可以得到整個寬帶內所有子頻帶信號的能量。如果能夠確定合理的判決門限γ，便可判斷每一個子頻帶的使用情況，確定感知向量。FFT快速運算即可滿足感知算法的實時性要求。

3.2 判決門限的選擇

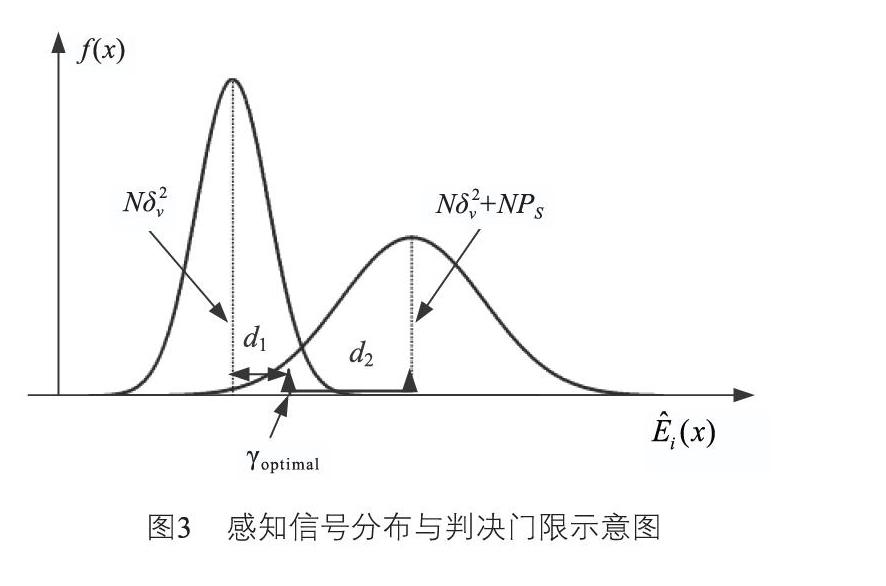
綜上所述，該方法所得的感知結果主要與判決門限的選擇有關。從公式（6）可以看出，當接收信號在H0和H1情況下，二者分布的方差不相等，所以判決門限不能簡單地視為二者期望的平均值。為找到綜合考慮虛警率和漏檢率的最佳判決門限γoptimal，記d1=γoptimal-Nδv，d2=Nδ2v+NPS-γoptimal分別為判決門限與H0、H1情況下能量期望的距離。在方差較大的H1時，其期望與判決門限距離應該較遠，以平衡虛警率和漏檢率，如圖3所示。于是借助切比雪夫不等式：

根據公式（10）：

由此可得最佳判決門限γoptimal為：

γoptimal

從上述表達式可以看出最佳判決門限主要取決于信噪比和噪聲功率。在實際系統中，需要估計這兩個參數，以求得最佳判決門限。

3.3 參數估計

通過上面的分析，實現寬帶頻譜感知需要估計噪聲功率和信噪比。通過對寬帶采樣信號的分析，可通過FFT運算，獲得寬帶中所有子頻段及其保護頻帶的功率譜信息。那么在高斯信道條件下，可以對該感知周期內的信噪比與平均高斯噪聲功率進行估計。

通常保護邊帶只包含了噪聲信息，基站的發送信號經過成型濾波后，旁瓣衰減很快，泄漏到保護帶的能量較小，可以認為是噪聲的一部分。利用保護頻帶內的平均功率，可以估計噪聲功率δv2 ，其中ω'代表邊帶頻率，B為保護邊帶寬度，△ω為信號子頻帶寬度。噪聲功率的公式為：

在高斯信道中，估計出噪聲功率之后，可求得信號總功率為：

其中，Ps_sum為有用信號總功率，Psum為感知帶寬內感知信號總功率。令lused為實際被占用的子頻帶數目，Ps為子頻帶上發射信號的平均功率。雖然鄰居節點的覆蓋半徑有可能不一樣，但是考慮到功率自適應調整，在各個小區邊緣用戶服務質量相同的情況下，可以認為不同節點的發送信號傳輸到其覆蓋邊緣時的功率基本相等，則Ps_sum為：

為求得信號平均功率Ps，采用如下迭代方法估計lused，然后代入公式（13）中求解可得Ps。迭代算法步驟如下：

其中，[·]運算代表四舍五入取整，q為迭代次數。在上述迭代運算中，

是對lused進行的估計值，當時，用對lused進行估計則包含了部分只有噪聲的子載波；反之，則有部分有信號子載波未被包含。令Pextra表示相應誤差所對應的多余或者遺漏的功率值，可表示為：

可寫為：

于是，求解使用子頻帶使用數量估計值為：

從公式（18）可以看出，有如下性質：

從公式（19）可以看出，經過多次迭代運算之后，會使得收斂于lused，并且該方法對初始門限γ0的取值不敏感，仿真結果也表明了這一點。的迭代運算結果趨近實際的子頻帶使用數量lused，從而求得信號平均功率與信噪比如下：

4 仿真結果

在進行仿真時，采用OFDM調制方式的LTE寬帶通信系統。在20MHz帶寬的LTE系統中，包含110個資源塊，每一個資源庫包含12個正交子載波[10]。主要仿真結果如圖4、圖5所示。給出了漏檢率與虛警率仿真曲線，分別同公式（7）、公式（8）中的理論曲線進行對比。

圖4與圖5分別表示漏檢率與虛警率。從仿真結果來看，仿真曲線與理論曲線基本契合，且在較低信噪比條件下，依然能夠獲得較低的漏檢率與虛警率，從而保證頻譜感知效率。并且，在對lused進行估計時，γ0取值從功率歸一化取值范圍為0.3至0.8，均可以在10次迭代計算以內收斂。然而在公式（6）中，將卡方分布近似成正態分布，存在一定誤差，這也是造成仿真曲線與理論曲線存在誤差的主要因素。

5 結束語

本文提出了一種快速寬帶頻譜感知方法，該方法能夠在高斯信道下，準確地估計出感知信號信噪比與平均噪聲功率，求得最佳判決門限。進而在一個感知周期內分別感知寬帶頻譜內每一個資源塊或頻點的使用情況，運算復雜度較低，有非常強的實時性，針對采用OFDM的LTE寬帶系統有良好的性能。通過仿真驗證可知，在較低信噪比條件時，其仍具有較低的虛警率與漏檢率，仿真結果曲線與理論曲線有很好的一致性。

參考文獻：

[1] Lee J， Yoon J， Song H， et al. Traffic pattern-based opportunistic spectrum access of cognitive femto base stations for decentralized cross-tier interference management[A]. Ubiquitous and Future Networks （ICUFN）， 2014 Sixth International Conf. on. IEEE， 2014： 352-356.

[2] Kay S M. Fundamentals of Statistical Signal Processing： Detection Theory[M]. Englewood Cliff， NJ： Prentice-Hall， 1988： 248-299.

[3] Wang C C， Wang D S， Chen S Y， et al. A wide range and high conversion gain power detector for frequency shift sensing applications[A]. Circuits and Systems （MWSCAS）， 2015 IEEE 58th International Midwest Symposium on IEEE， 2015： 1-4.

[4] Poor H V. An Introduction to Signal Detection and Estimation[M]. New York： Springer-Verlag， 1998： 50-150.

[5] Enserink S， Cochran D. A cyclostationary feature detector[J]. Signals Systems and Computers， 1994（2）： 806-810.

[6] Axell E， Leus G， Larsson E G， et al. Spectrum sensing for cognitive radio： State-of-the-art and recent advances[J]. Signal Processing Magazine， IEEE， 2012，29（3）： 101-116.

[7] Sun H， Nallanathan A， Wang C X， et al. Wideband spectrum sensing for cognitive radio networks： a survey[J]. Wireless Communications， IEEE， 2013，20（2）： 74-81.

[8] Sun H， Chiu W Y， Jiang J， et al. Wideband spectrum sensing with sub-Nyquist sampling in cognitive radios[J]. IEEE Transactions on Signal Processing， 2012，60（11）： 6068-6073.

[9] MacKenzie A B， Reed J H， Athanas P， et al. Cognitive radio and networking research at Virginia Tech[J]. Proceedings of the IEEE， 2009，97（4）： 660-688.

[10] Sesia S， Toufik I， Baker M. LTE： the UMTS long term evolution[M]. New York： John Wiley & Sons， 2009.