激發興趣，體驗成功，培養學生創造性思維

楊基玉

數學是思維的體操，教學中培養學生的創造性思維，發展學生的創造能力，是現代教育的出發點和歸宿。在數學教學過程中，一個重要任務就是培養學生的創造性思維。但學生數學思維的培養不是一朝一夕的事，它寓于教學的全過程。作為一名數學教師，絕對不能忽視培養學生的數學思維能力。在教學中，教師應自始至終以培養學生的創造性思維為核心，鼓勵學生多動腦，教會學生怎樣想。本文結合實際教學，就如何在數學教學中培養學生的創造性思維，并促使學生能力發展展開探討。

一、學習興趣是激發學生創造性思維的前提

興趣，是創造性思維素質的成分之一，在創造性思維中具有觸發與催化的作用。在學習活動中，學生的學習是一種有意識的行動，需要一種能夠激勵、推動他們去學習的內部動力，從而達成學習的目的，而這種內部動力產生于學習需要，只有當學生有了學習數學知識的需求和愿望，才能積極主動地參與到學習活動中，教學才能煥發出生命的光彩。

例如，教學“兩位數加、減兩位數口算”一課。筆者先用卡片出示一組計算題，要求學生迅速口算，對于最初的幾道“兩位數加減整十數、一位數”的題目，學生紛紛搶答，且正確率高。當學生沉浸在自我滿足，欣喜于自己的表現時，筆者突然出示算式“28+37=？”。筆者鼓勵學生說一說自己在計算時的思考。這時，學生各抒己見，廣泛地展開討論。有的學生按照筆算的方法在大腦中擺個算式，從低位算起；有的學生先算20+30=50，8+7=15，再算50+15=65。筆者對想出不同方法的學生給予鼓勵，在學生情緒高漲時，再告訴他們：“這道題還有更簡便的口算方法，即28+30=58，58+7=65。”使學生記憶深刻，提高他們的思維靈活性。首先，像這樣利用學生已有的知識經驗，人為地制造認識沖突，將課題教學巧妙地融于問題情境中，毫無疑問能夠激發學生對學習新知的強烈好奇心和求知欲。其次，鼓勵學生憑借自己的智慧和才能，積極、獨立地思考問題，力求打破常規，不拘泥、不守舊，尋求新的角度，探究不同的解題方法，解決更多的問題。這樣的思維是全新的，具有批判性、廣闊性、獨特性、敏捷性、靈活性等特點。凡事多思、多想，從多方面、多角度，創造性地解決問題，促進思維能力的發展和思維水平的提高，進而達到提高學生分析、解決問題的能力。

二、獲得成功體驗是學生培養創造性思維的原動力

教師在教學中要適時激發學生的求知欲，還要讓學生在自主學習中獲得成功的情感體驗。只有這樣，學生的思維才會敏捷，才可能進行創造。因此，發揮評價的作用，把激勵帶進課堂，積極為學生創造表現自我的機會，并想方設法幫助他們獲得不同程度的成功，體現自身的價值，才能產生“親其師而信其道”的心理效應。使學生產生最佳的學習心態和求知的主動性、積極性。

對學生在課堂上發表的見解，發現問題、完成練習等，教師都應給予積極的評價。如“真不錯”“你說得太好了”“別緊張，再想一想，老師知道你能行”等。對于未獲得成功的學生，教師不能簡單地給予批評指責，在他們的解題思路中，教師應該盡量發現其錯誤中的正確成分，予以肯定，并啟發學生自己思考發現，糾正錯誤。

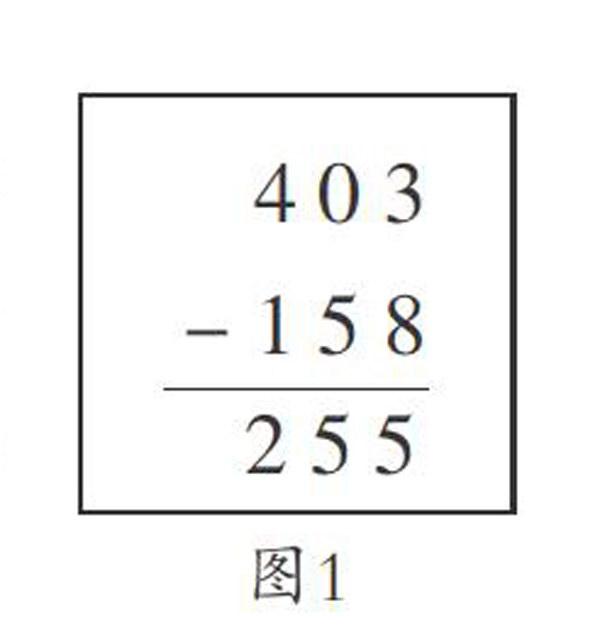
例如，教學“被減數中間有零的連續退位減法”一課。筆者在出示“403-158=？”后，讓學生嘗試列豎式計算，有位學生板演這樣列式（圖1）。

這時，班上有個別同學發出唏噓聲。筆者問：“看來大家都挺有想法，再仔細觀察，看一看有計算正確的步驟嗎？找一找哪些地方是正確的，哪些地方是錯誤的？”板演的學生眼前一亮，也積極加入“尋找”的隊伍中。不一會兒，學生們紛紛舉手：“個位、百位計算正確，十位點了退位點卻忘了退1。”筆者：“是呀，被減數中間有零的連續退位減法中，哪一位上不夠減，要從前一位退1，這位同學說得非常好，個位不夠減，從十位退1，而十位是0，又需要從百位退1。這位同學只是在十位上點了退位點，卻忘了退1再減。”通過這樣糾錯、發現的過程，學生們對于被減數中間有零的連續退位減法的算理理解更深刻了。同時，也讓學生養成糾錯中不但要發現他人解題中的錯誤，更要發現其中正確的地方。這樣的處理，既教育了其他學生，又給了板演的學生爭取成功的機會，使學生在探究新知或遇到解題困難（挫折）時，能始終保持積極向上的樂觀情緒，努力探求獲得成功的強烈愿望。

三、實踐操作是培養學生創造性思維的良好方式

“手和腦有著千絲萬縷的聯系，手使腦得到發展，使它更明智；腦使手得到發展，使它變成思維的工具和鏡子。”（蘇霍姆林斯基）可見，數學學習活動需要實踐，需要學生親身經歷。雖然現代多媒體技術走進了課堂，但無論問題情境設計得多么完美、新穎、生動，學生只是從大屏幕中，以及教師完美的敘述里去模擬建構，抑或與生活中的所見所聞進行對照、類比。學生如果沒有在數學活動中親身體會，理解也難以深刻。所以，在教學中，教師要注重給學生創設動手操作的機會和平臺，讓學生在操作中創造性地發現真理。

例如，教學“有余數的除法”一課。面對二年級的學生，筆者讓他們從動手實踐中感知———先讓學生把9根小棒平均分給3個小朋友，再把9根小棒平均分給4個小朋友，看看結果怎么樣？在實際操作中讓學生通過比較的方法認識有余數的除法和余數，再抽象到算式。接著把12塊小木塊平均分給5個小朋友，學生都能想出正確的結果。這時，筆者又進一步提問：把16塊小木塊也平均分給5個小朋友，結果剩下多少個？有些學生順勢就說剩下6個，有的學生不同意，便產生了分歧。筆者請學生具體分一分，讓實踐來證明誰是正確的，引導學生歸納出余數要比除數小的結論。以上教學過程，都是在教師的引導下由學生獨立完成的。學生看到了自己創造性的“發現”，無不為之動容。他們在動手操作中發現真理，培養了創新能力。

（作者單位：福建省平潭縣嵐城鄉中心小學 責任編輯：王彬）