尖軌降低值超限對轉轍器動力特性的影響研究

馬曉川， 王 平， 王 健， 徐井芒

(西南交通大學 高速鐵路線路工程教育部重點實驗室， 四川 成都 610031)

高速道岔轉轍器處，由于尖軌頂面降低，開始階段的輪軌接觸點位于基本軌上，并隨尖軌頂寬的增大逐漸外移，直到輪軌接觸點由基本軌過渡到尖軌上。這個過程中，輪對在橫向蠕滑力的作用下會向尖軌方向偏離。當輪對中心偏離軌道中心線時，左右車輪將以不同的滾動圓半徑向前運行，輪對中心的運動軌跡呈波形曲線，稱為輪對的蛇行運動[1-2〗。道岔轉轍器處的動力性能是道岔研究內容的重點，當輪對發生擺動時會惡化輪軌動力作用。

尖軌降低的位置和大小是影響道岔轉轍器動力特性的重要因素，許多學者針對轉轍器的動力特性進行了研究。文獻[3〗提出了求解道岔轉轍器輪載分布規律的計算模型和方法。文獻[4〗提出了車輛道岔系統動力學理論。文獻[5〗運用車輛道岔系統動力學的方法，研究了轉轍器軌距優化技術對高速道岔動力性能的影響。文獻[6〗建立了道岔動力參數設計法，并對道岔轉轍器部分的軌距加寬進行了優化設計。

本文針對42號高速道岔存在尖軌降低值超限的問題，運用車輛-道岔系統動力學理論，通過仿真計算研究尖軌降低值超限對道岔轉轍器處輪載過渡、車輛穩定、輪軌動力附加力、行車安全指標等的影響。

1 尖軌降低值及輪廓變化

1.1 尖軌降低值測量結果

使用深度尺對42號高速道岔直尖軌相對于曲基本軌的頂面降低值逐枕進行了測量，測量降低值與設計降低值的對比見圖1。可見，該道岔直尖軌實際降低值普遍大于設計值，特別是在輪載從基本軌向尖軌過渡的范圍內降低值偏差較大，最大值約2.3 mm，已超過TB/T3302—2013《高速鐵路無砟軌道道岔鋪設技術條件》[1〗中“尖軌與基本軌頂面高度偏差不大于1 mm”的規定。

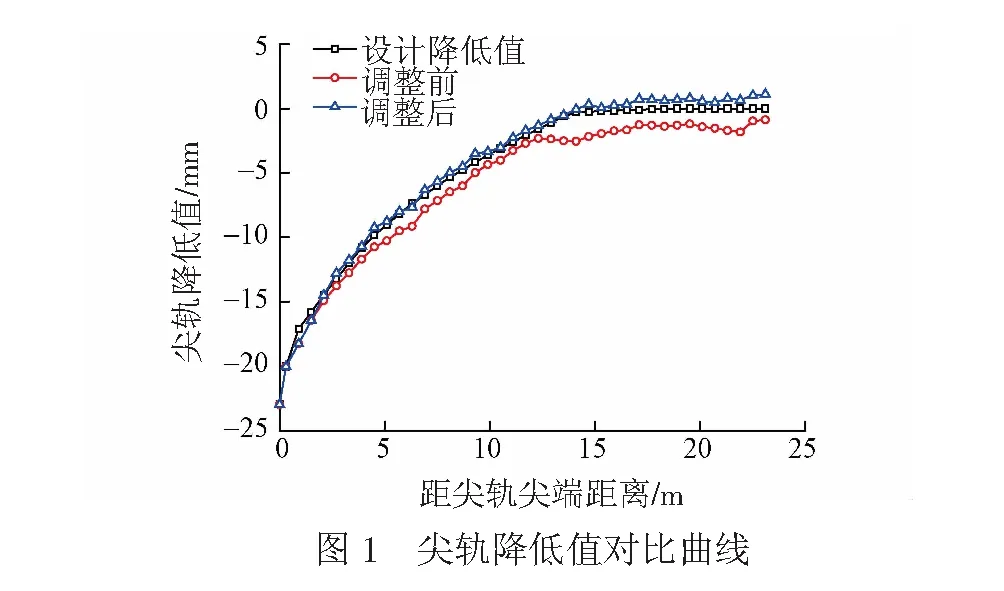
動車組以295 km/h的速度直向通過該道岔時，在轉轍器處會出現較為嚴重的晃車現象。根據尖軌降低值的偏差，在尖軌軌底和滑床臺板之間設置不同厚度的鐵墊片使尖軌抬高。由于現場條件及道岔本身結構的限制，調整后的尖軌降低值與設計降低值存在一定的偏差，但偏差被控制在1 mm之內。

1.2 尖軌輪廓變化

當實測尖軌降低值與設計降低值不符時，尖軌和基本軌的“組合輪廓”會隨之發生變化。根據測得的尖軌降低值的偏差，分別得到尖軌頂寬20、35、50 mm三個關鍵斷面處的輪廓變化，見圖2。

2 計算理論

參考文獻[4〗和文獻[8〗，建立車輛-道岔系統耦合振動模型。該模型包含3個部分，分別是車輛模型、道岔模型和輪軌接觸模型。

2.1 車輛模型

道岔區的車輛模型與區間線路的車輛模型相同。本文為了更好地模擬車輛經過道岔時的動力特性，采用整車模型。車輛模型見圖3。

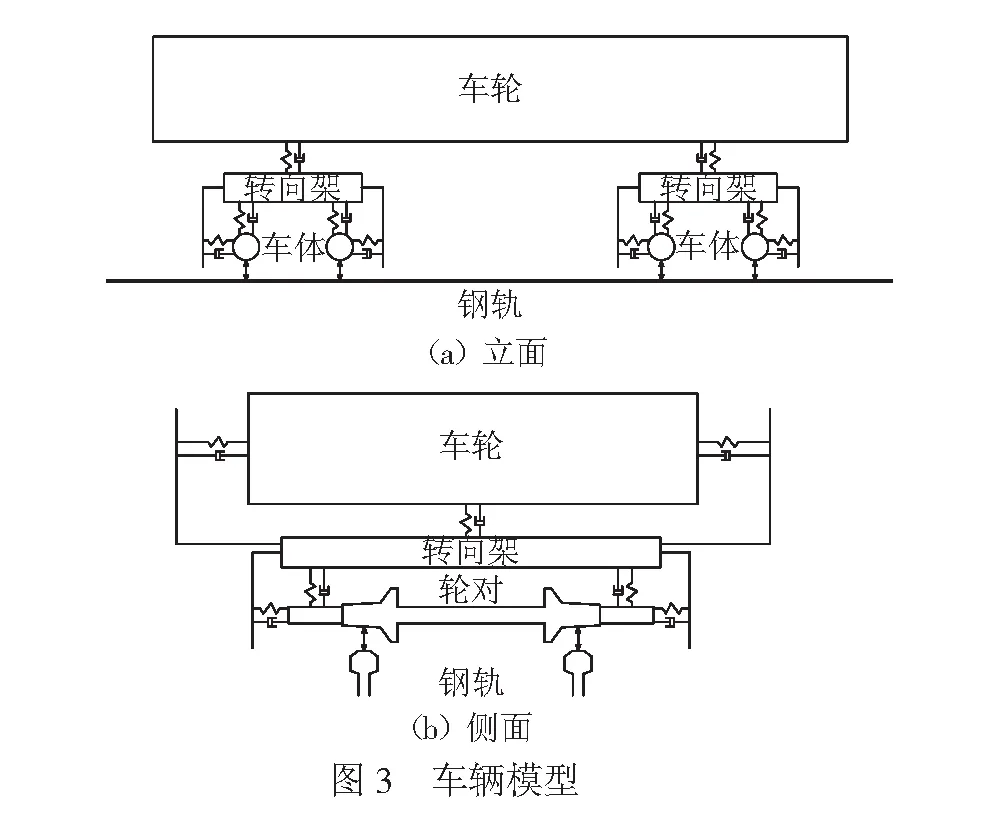
在車輛模型中，考慮31個運動自由度：車體有橫移、沉浮、側滾、點頭和搖頭5個自由度；2個轉向架分別有橫移、沉浮、側滾、點頭和搖頭5個自由度;4個車輪分別有橫移、沉浮、側滾和搖頭4個自由度。

計算模型坐標系的選取為：以車輛前進方向為x軸正方向，以車輛前進方向的右側為y軸正方向，z軸正方向根據右手法則確定。

車輛的基本計算參數包括車體、轉向架和輪對的質量，繞各軸的慣性矩，一、二系懸掛的剛度和阻尼。本文的車輛基本計算參數取自文獻[8〗，見表1。

表1 車輛基本計算參數

2.2 道岔模型

根據42號高速道岔的設計圖建立42號可動心軌高速道岔整體模型，見圖4。

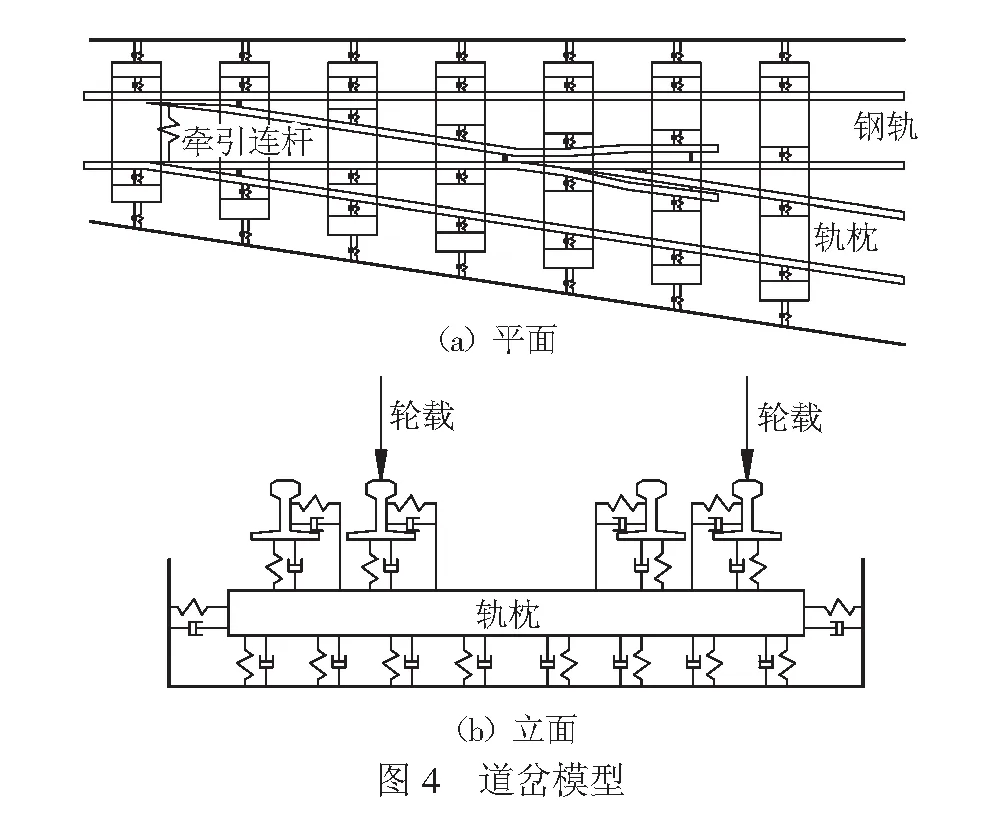
在道岔模型中，將道岔中的每根鋼軌按軌枕支承點劃分為有限個梁單元，每個單元節點有垂向位移、垂向轉角、橫向位移及橫向轉角4個自由度。軌枕在橫向上被視為一個剛體質量塊，具有橫向位移1個自由度。在垂向上將軌枕按鋼軌支承點劃分為有限個梁單元，每個單元具有垂向位移和垂向轉角2個自由度。

42號高速道岔的基本計算參數見表2。

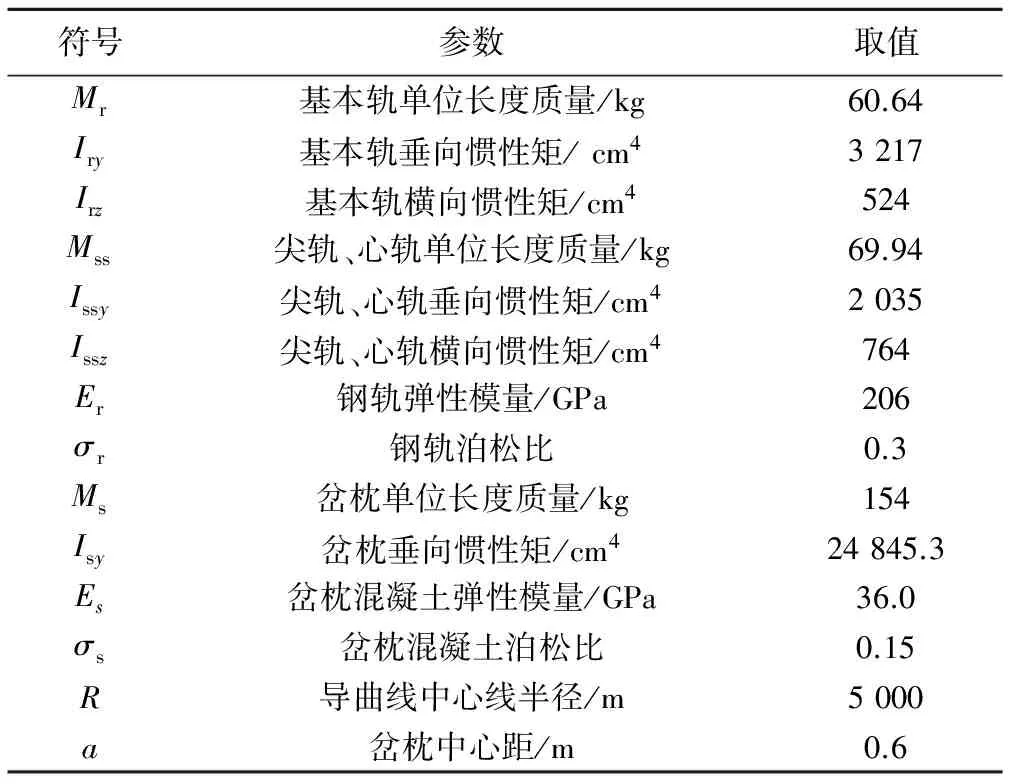
表2 道岔基本計算參數

2.3 輪軌接觸模型

車輛模型和道岔模型之間由輪軌接觸模型建立關聯。在輪軌接觸模型中，考慮車輪與鋼軌踏面的接觸關系、車輪輪緣與鋼軌的接觸關系和車輪輪背與翼軌的接觸關系。同時，考慮車輛運行至道岔不同部位時接觸軌跡的變化。

輪軌垂向作用由非線性的赫茲接觸彈簧力反映，輪軌橫向作用由輪軌蠕滑力和輪緣力等反映，考慮車輪與基本軌、尖軌以及車輪與翼軌、心軌可能發生的多點接觸情況。

2.4 振動方程

采用變分形式的最小勢能原理方法，建立道岔輪軌振動系統的微分方程。由最小勢能原理可知，在所有滿足邊界條件的協調位移中，滿足平衡條件的位移可以使系統的總勢能π達到極值，即

δπ=δ(U+V)=0

( 1 )

式中:U、V分別為系統的總應變能和總外力勢能。

以大地為參考坐標系，以軌道及車輛均不受外力狀態為初始狀態，推導系統中各個能量的變分表達式及變分形式的位移協調條件，經計算機對號入座形成系統的質量矩陣M、剛度矩陣K及阻尼矩陣C，并組成系統的振動微分方程如式( 2 )所示

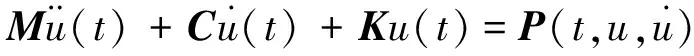
( 2 )

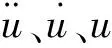
利用系統的振動微分方程，在某一時間步長下，迭代判斷協調位移能否滿足系統平衡條件。若不滿足則重新組建新的振動微分方程，直到滿足要求為止。如此可得到該時刻的系統振動響應。

2.5 計算模型驗證

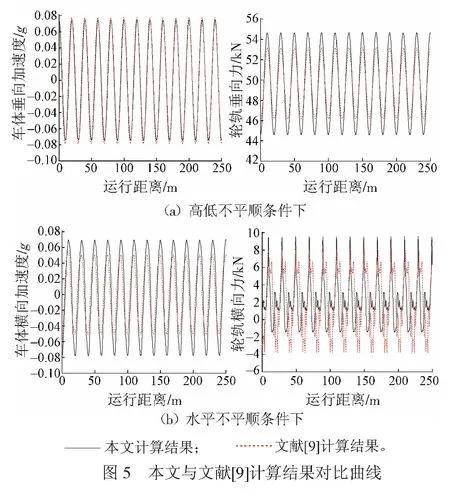
文獻[10〗中建立了車輛-軌道空間模型，并通過與NUCARS和SIMPACK商業軟件數值仿真結果的對比驗證了其計算結果的可靠性。車輛進入道岔前，本文的計算結果與文獻[9〗計算結果的對比見圖5。計算時車速取為160 km/h，軌道不平順采用的是單一的諧波型高低和方向不平順，該不平順可按式( 3 )進行描述

Y=0.5Asin(2πx/λ)

( 3 )

式中：A為不平順的全峰值，取為10 mm；λ為不平順波長，取為20 m；x為線路的縱向距離。

由圖5可見:當軌道只存在高低不平順時，與文獻[10〗計算結果相比，本文計算結果中車體的垂向加速度基本吻合，輪軌垂向力的波動范圍略大，兩者的變化規律大致相同；當軌道只存在水平不平順時，與文獻[9〗計算結果相比，本文計算結果中車體橫向加速度的波動范圍略大，輪軌橫向力的最大值略大，兩者的變化規律大致相同。這說明本文所使用的計算模型可以較為真實可靠地反映車輛-軌道系統的振動特性。

3 計算結果分析

本文的計算是基于車輛-道岔系統動力學理論，應用SIMPACK動力學軟件，通過仿真計算可分別得到動車組車輛以295 km/h的速度直向通過道岔和以120 km/h的速度側向通過道岔時，道岔鋼軌接觸點的位移、輪對橫向位移、車體橫向加速度、輪軌橫向及垂向動力附加力、脫軌系數、減載率等道岔動力性能參數。

3.1 轉轍器輪載過渡

基于輪軌接觸跡線法[11-12〗的基本原理，計算得到設計尖軌降低值條件下與尖軌降低值超限條件下尖軌關鍵斷面處輪軌接觸點對分布的對比，設計尖軌降低值條件下輪軌接觸點對的分布見圖6，尖軌降低值超限條件下輪軌接觸點對的分布見圖7。

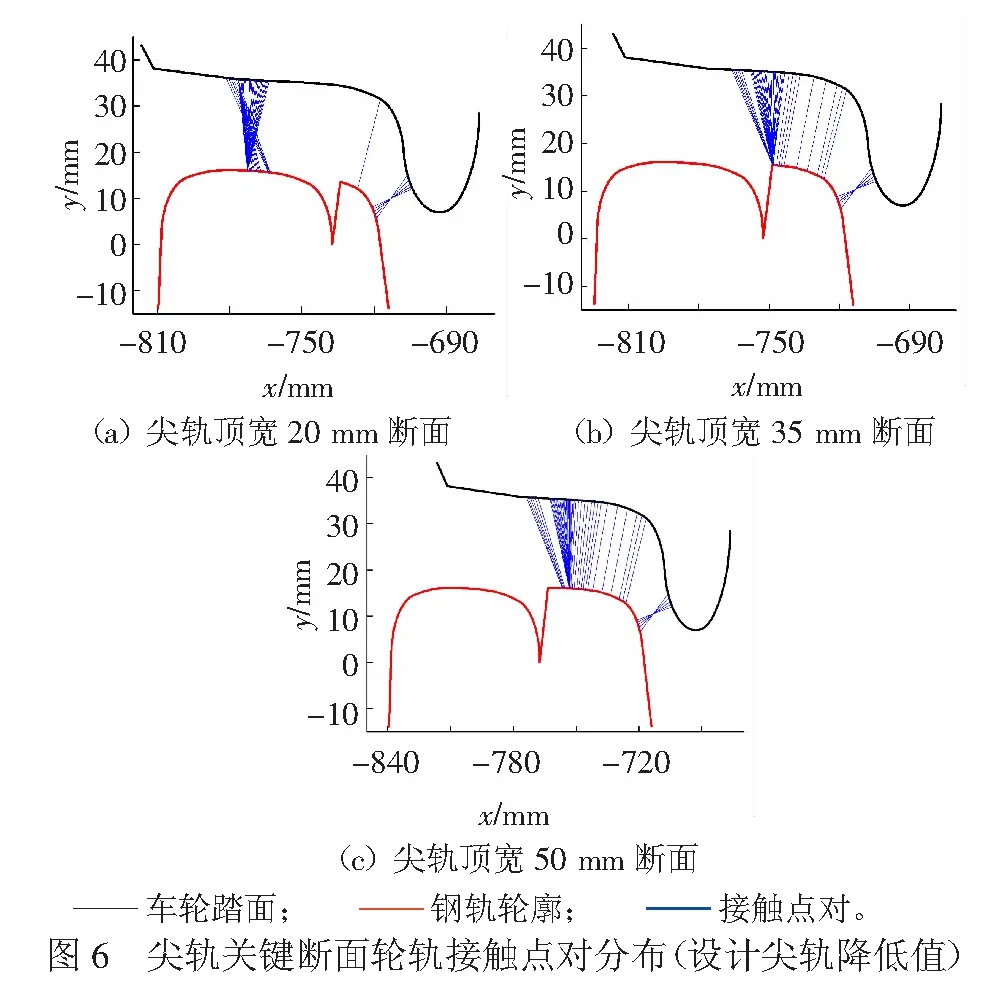
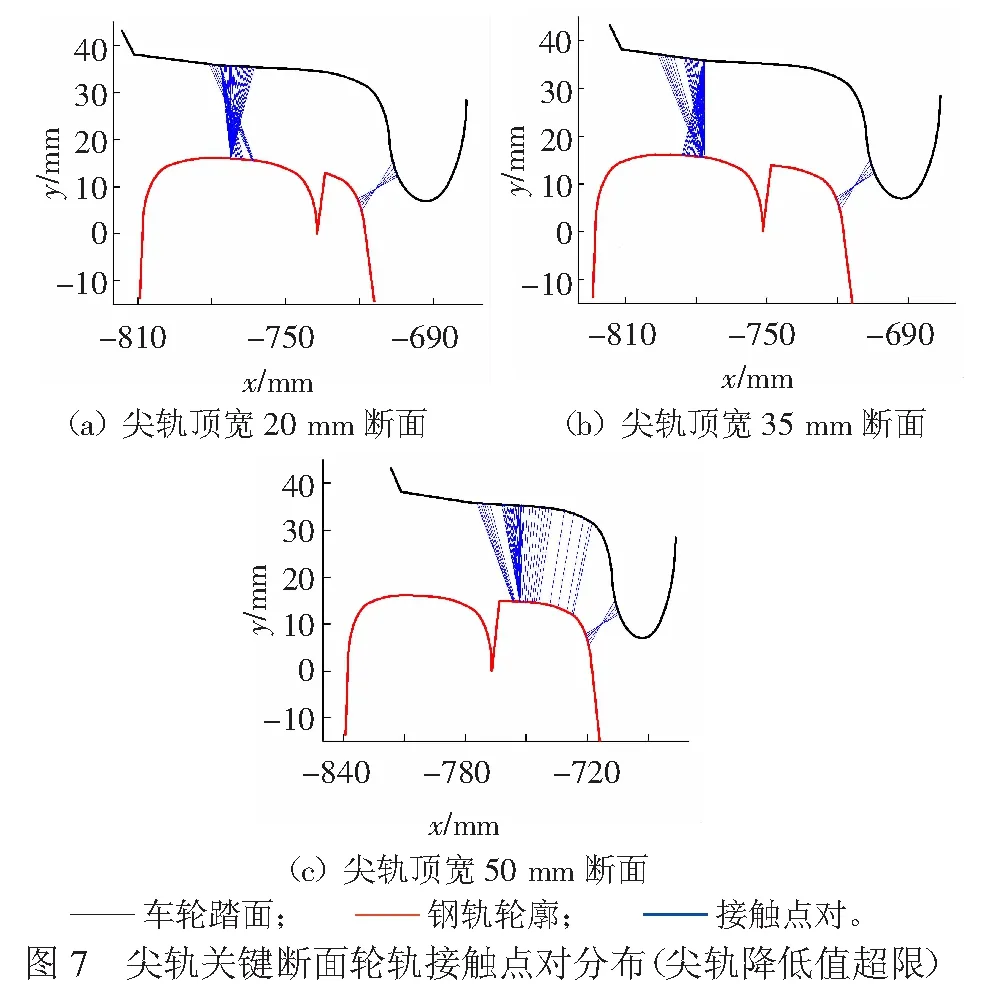
車輛經過道岔轉轍器時，開始階段輪軌接觸點主要分布在基本軌上，當車輪位于轉轍器輪載過渡段時，輪軌接觸點逐漸由基本軌過渡到尖軌上，最后輪軌接觸點全部過渡到尖軌上。

圖8所示為車輪從尖軌尖端運行到到尖軌跟端過程中，車輪荷載在基本軌上的比例系數變化規律。可見車輪荷載完全作用在基本軌上時，比例系數為1；反之，車輪荷載完全作用在尖軌上時，比例系數為0。

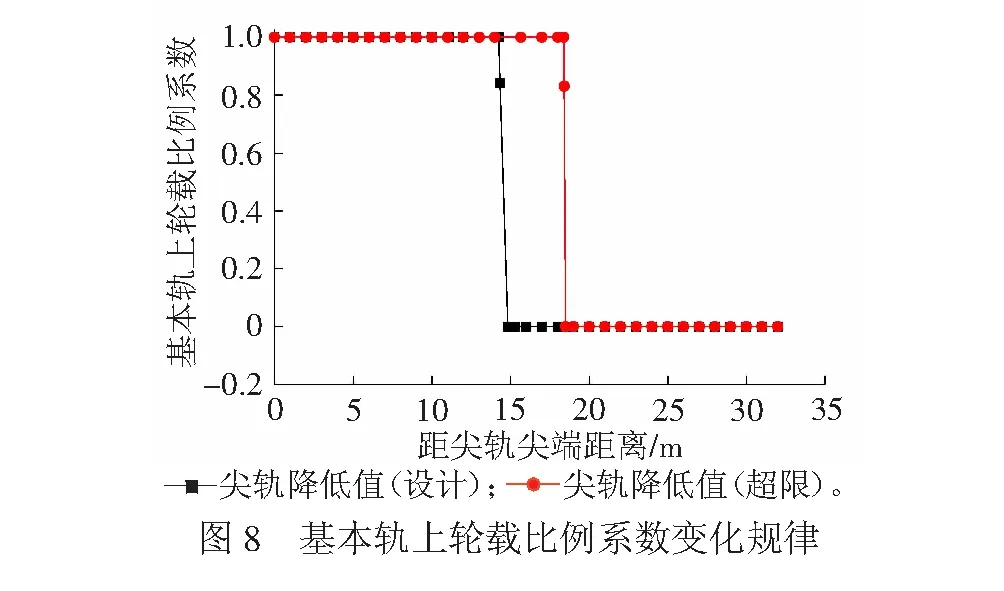
由圖8可知：設計尖軌降低值條件下，輪載過渡段在距尖軌14.236～14.822 m，過渡段長度約586 mm；尖軌降低值超限條件下，輪載過渡段在距尖軌18.393～18.507 m，長度約為114 mm，與設計尖軌降低值條件相比明顯后移和縮短。這說明尖軌降低值超限使得輪載過渡的起點后移且發生輪載過渡的時間明顯減小。

由圖6～圖8可知，尖軌頂寬35 mm斷面處，設計尖軌降低值條件下，輪軌接觸點已由基本軌全部過渡到尖軌上，尖軌降低值超限條件下，輪軌接觸點依然分布在基本軌上，說明尖軌降低值超限引起輪載過渡段的起點后移。

設計尖軌降低值條件、降低值超限調整前及調整后3種工況下計算的鋼軌接觸點位置的變化規律見圖9。

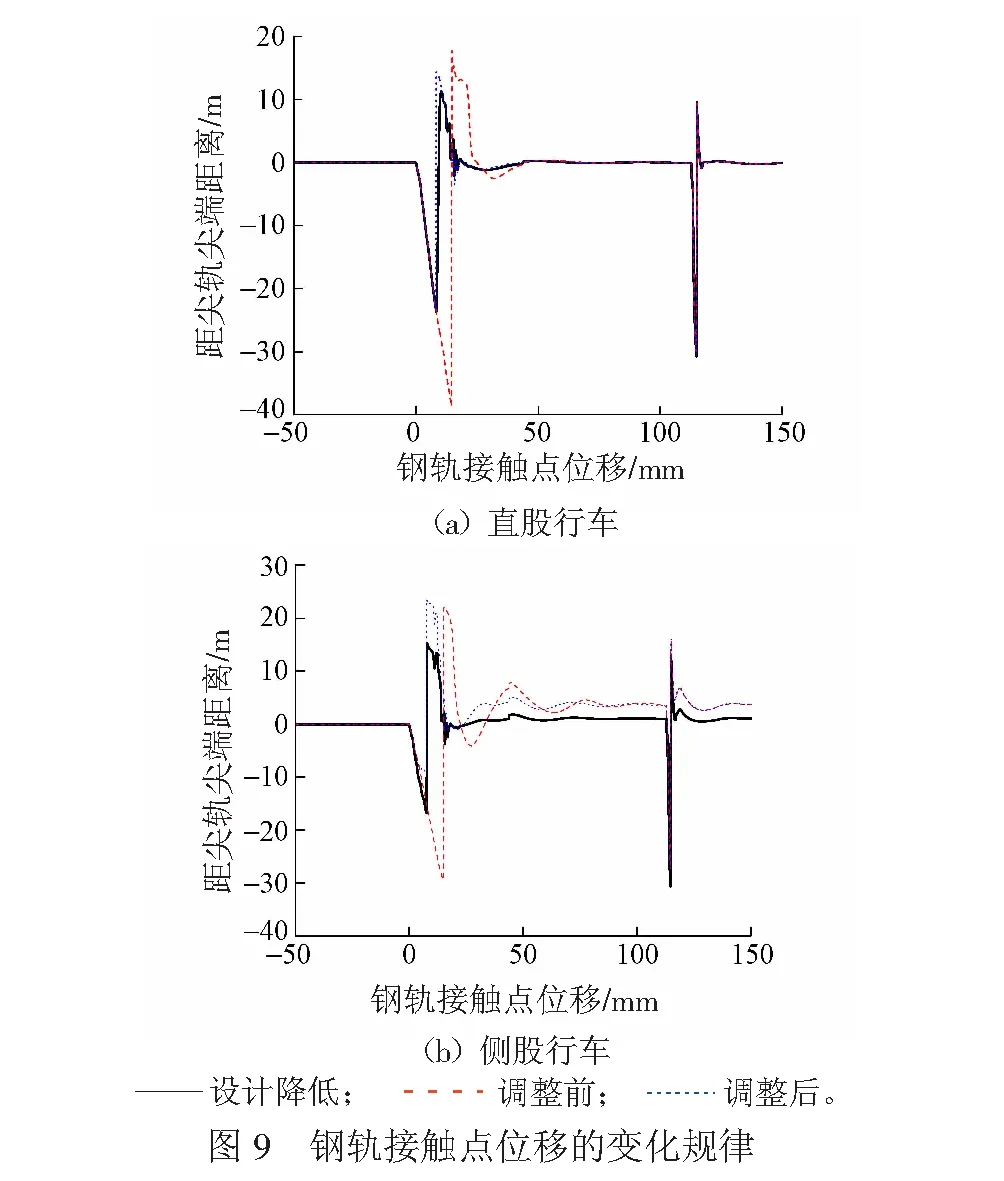
由圖9(a)可知：直股行車時，開始階段鋼軌接觸點不斷外移，設計尖軌降低值條件下，鋼軌接觸點的外移幅值為23.3 mm；尖軌降低值超限調整前，鋼軌接觸點的外移幅值達到38.7 mm，為設計條件下的1.66倍；尖軌降低值超限調整后，鋼軌接觸點的外移幅值為23.3 mm，與設計條件下一致。尖軌降低值超限時，轉轍器處輪載過渡的起點發生后移現象，后移量約為6.4 m，與靜力分析結果一致。由圖9(b)可知：側股行車時，開始階段鋼軌接觸點不斷外移，設計尖軌降低值條件下，鋼軌接觸點的外移幅值為16.8 mm；尖軌降低值超限調整前，鋼軌接觸點的外移幅值達到29.3 mm，為設計條件下的1.74倍；尖軌降低值超限調整后，鋼軌接觸點的外移幅值為9.1 mm，與設計條件相比偏小。尖軌降低值超限時，轉轍器處輪載過渡的起點發生后移現象，后移量約為7.3 m，亦與靜力分析結果一致。

尖軌降低值超限時，道岔轉轍器輪載過渡起點的后移加大輪對通過轉轍器時蛇行運動的距離和幅度，加劇輪對的擺動，最終會導致輪軌動力作用惡化，影響行車。尖軌降低值超限調整后，轉轍器輪軌過渡的起點回復到設計條件的位置，減小了輪對通過道岔轉轍器時的擺動，有利于車輛安全平穩地通過道岔轉轍器。

3.2 車輛穩定

尖軌降低值設計條件、降低值超限調整前及調整后3種工況下計算的輪對橫向位移的變化規律，見圖10。

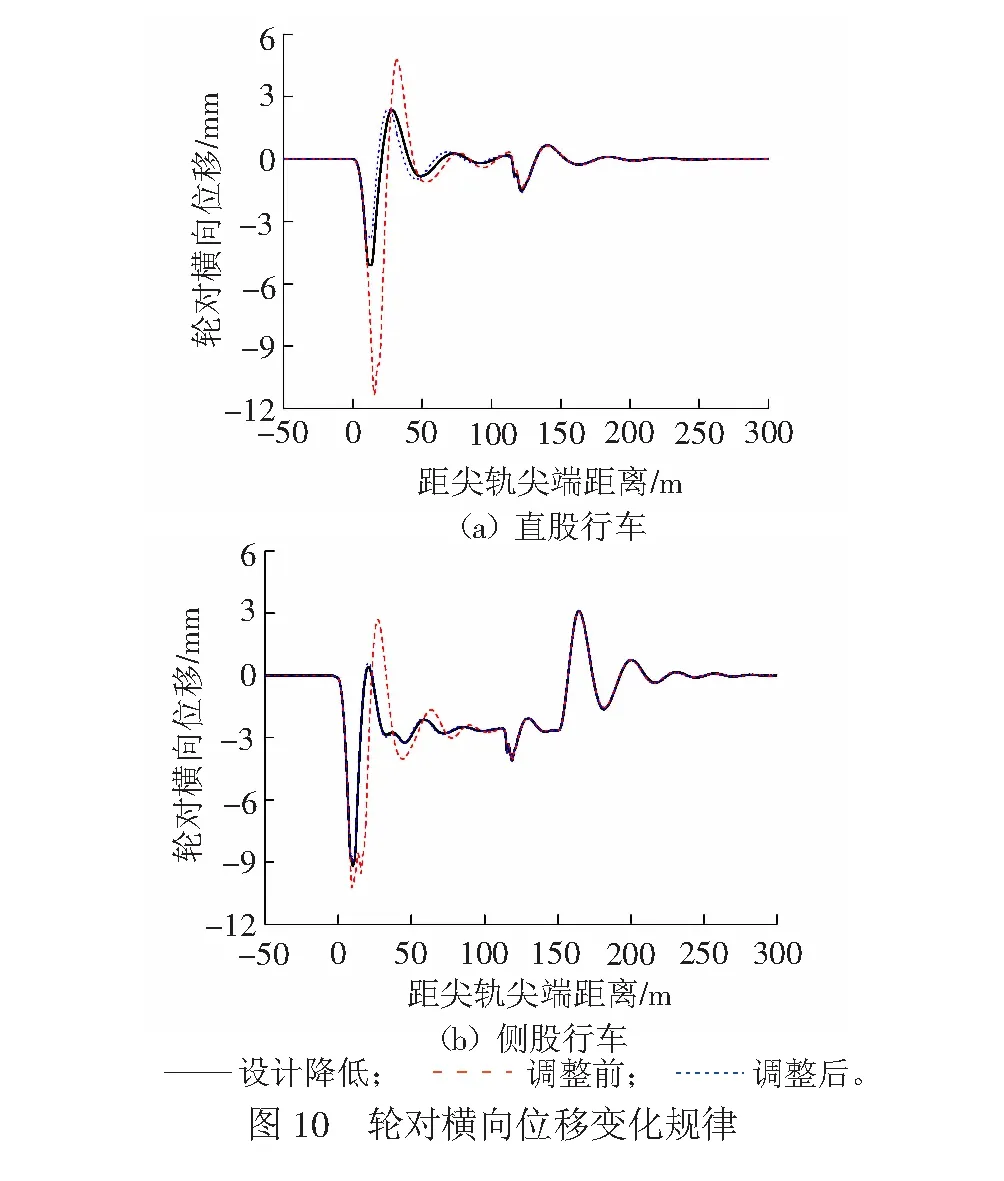
由圖10(a)可知：直股行車時，設計尖軌降低條件下，輪對橫向運動的幅值為5.1 mm；尖軌降低值超限調整前，輪對橫向運動的幅值為11.3 mm，為設計條件下的2.2倍；尖軌降低值超限調整后，輪對橫向運動的幅值為3.82 mm，較設計條件下有所減小。由圖10(b)可知：側股行車時，設計尖軌降低條件下，輪對橫向運動的幅值為9.2 mm；尖軌降低值超限調整前，輪對橫向運動的幅值為10.2 mm，相比設計條件略有增大；尖軌降低值超限調整后，輪對橫向運動的幅值為9.0 mm，較設計條件下略有減小。

尖軌降低值設計條件、降低值超限調整前及調整后3種工況下計算的車體橫向加速度的變化規律見圖11。

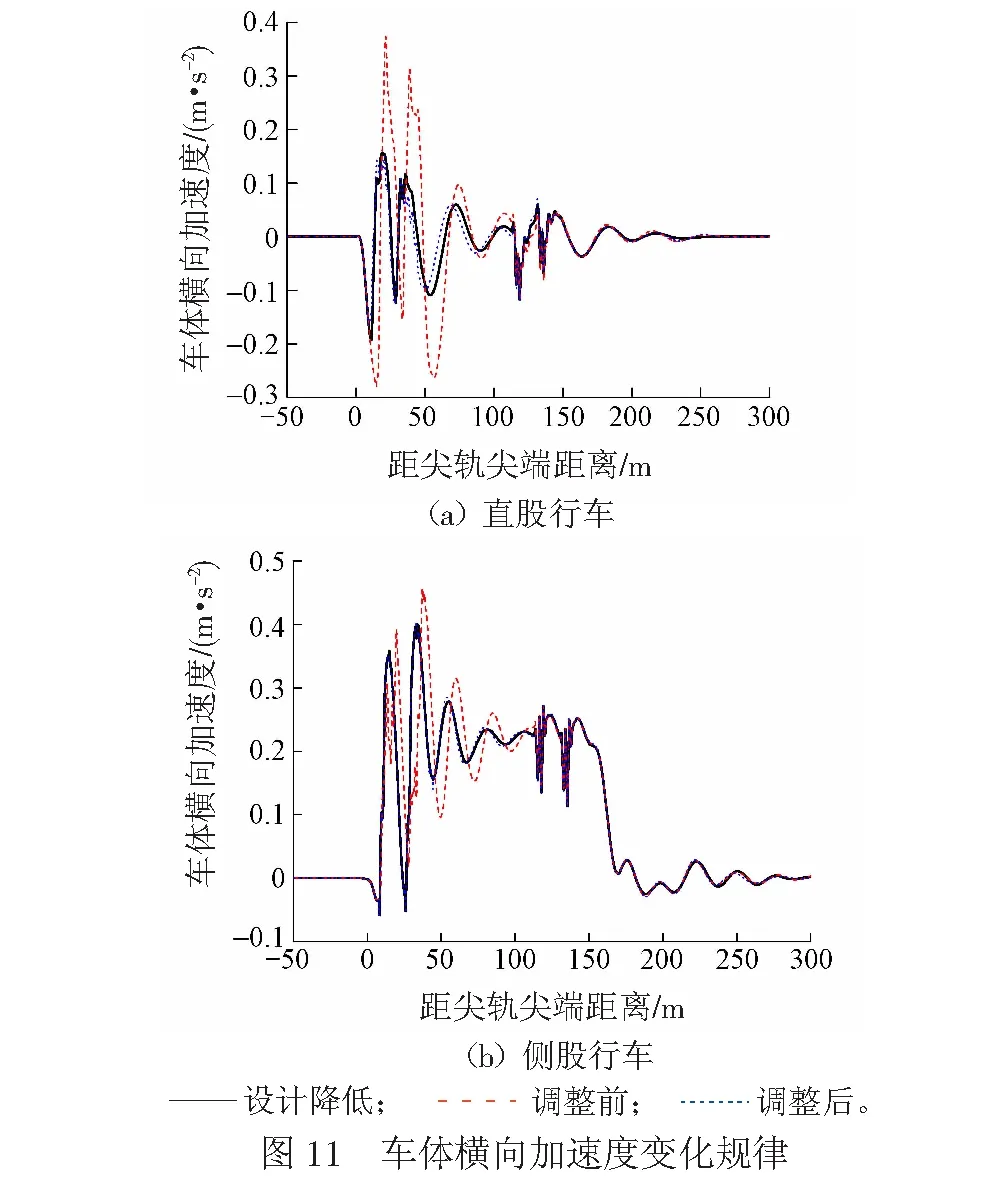
由圖11(a)可知：直股行車時，設計尖軌降低條件下，車體橫向加速度的幅值為0.193 m/s2；尖軌降低值超限調整前，車體橫向加速度的幅值為0.374 m/s2，為設計條件下的1.9倍；尖軌降低值超限調整后，車體橫向加速度的幅值為0.164 m/s2，相比設計條件下有所減小。由圖11(b)可知：側股行車時，設計尖軌降低條件下，車體橫向加速度的幅值為0.400 m/s2；尖軌降低值超限調整前，車體橫向加速度的幅值為0.457 m/s2，為設計條件下的1.2倍；尖軌降低值超限調整后，車體橫向加速度的幅值為0.401 m/s2，與設計條件下的基本相同。

由直股行車時3種工況下輪對橫向位移變化規律和車體橫向加速度變化規律可知，與設計尖軌降低值條件相比，尖軌降低值超限工況下車輛通過道岔轉轍器時，輪對的橫向位移幅值和車體橫向加速度幅值均顯著增大，約為設計條件下的2倍，容易引起晃車現象，解釋了現場車輛通過轉轍器時存在的晃車現象。尖軌降低值調整后，車輛通過道岔轉轍器時，輪對橫向位移幅值和車體橫向加速度幅值相比設計條件均有一定程度的減小，說明調整尖軌降低值有效。

3.3 輪軌動力附加力

尖軌降低值設計條件、降低值超限調整前及調整后3種工況下計算的輪軌橫向和垂向動力附加力的變化規律見圖11、圖12。

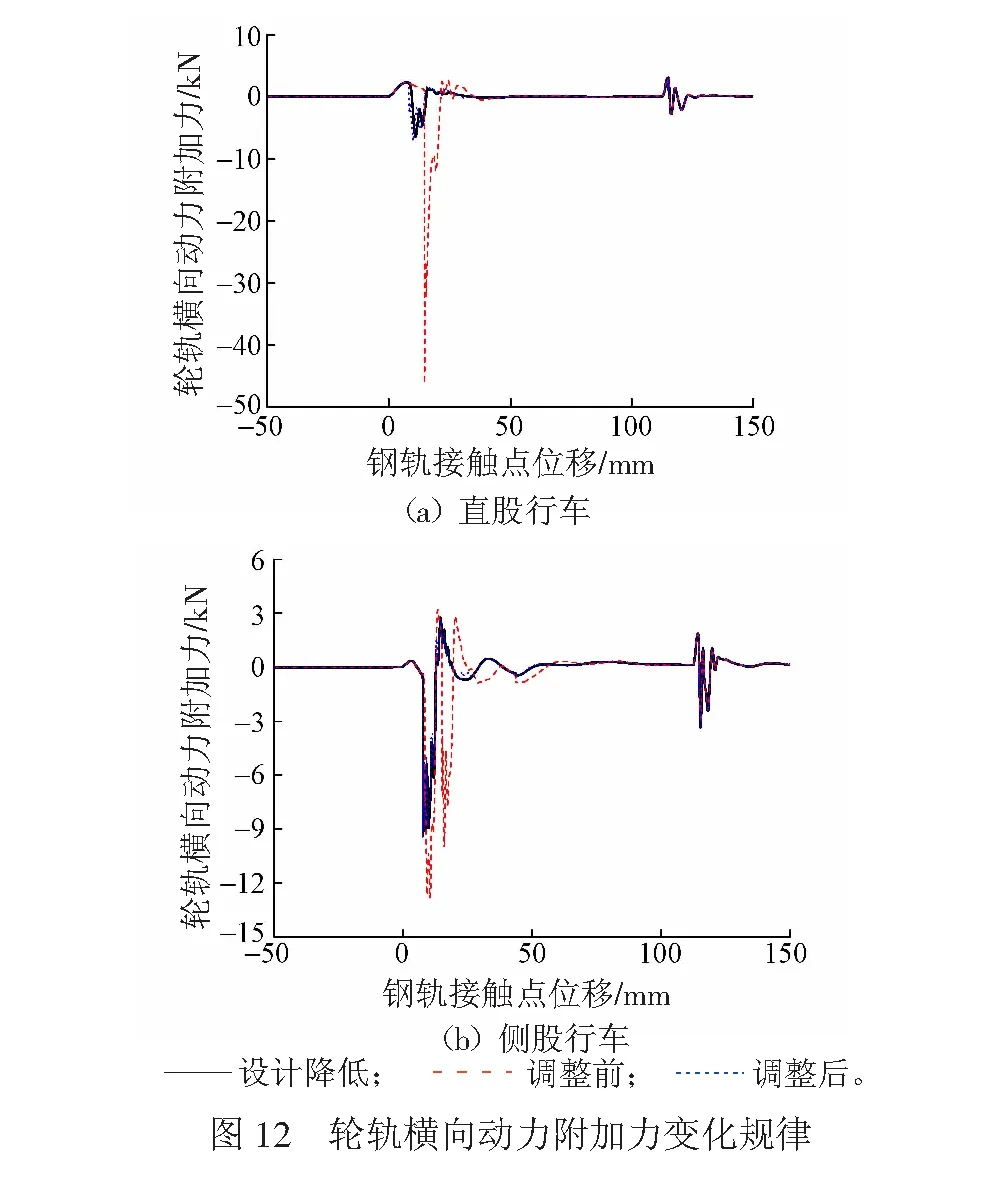
由圖12(a)可知：直股行車時，尖軌降低值設計條件下，輪軌橫向動力附加力幅值為6.29 kN；尖軌降低值超限調整前，輪軌橫向動力附加力幅值為46.28 kN，為設計條件下的7倍；尖軌降低值超限調整后，輪軌橫向動力附加力幅值為6.98 kN，較設計條件有所增大。由圖12(b)可知：側股行車時，尖軌降低值設計條件下，輪軌橫向動力附加力幅值為9.06 kN；尖軌降低值超限調整前，輪軌橫向動力附加力幅值為12.83 kN，為設計條件下的1.4倍；尖軌降低值超限調整后，輪軌橫向動力附加力幅值為8.99 kN，較設計條件略有減小。

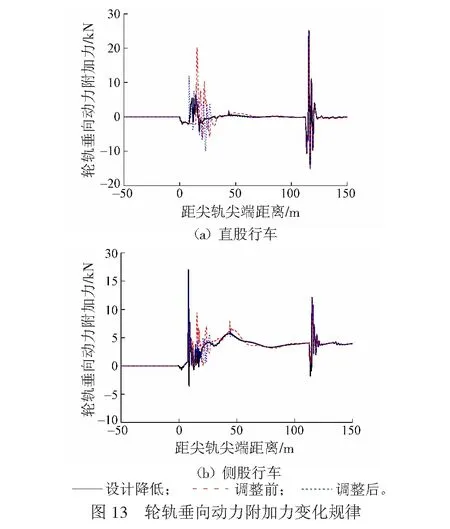
由圖13(a)可知：直股行車時，尖軌降低值設計條件下，輪軌垂向動力附加力幅值為5.73 kN；尖軌降低值超限調整前，輪軌垂向動力附加力幅值為20.04 kN，為設計條件下的3.5倍；尖軌降低值超限調整后，輪軌垂向動力附加力幅值為10.98 kN，較設計條件有所增大。由圖13(b)可知：股行車時，尖軌降低值設計條件下，輪軌垂向動力附加力幅值為16.97 kN；尖軌降低值超限調整前，輪軌垂向動力附加力幅值為9.51 kN，較設計條件有較大的減小；尖軌降低值超限調整后，輪軌垂向動力附加力幅值為16.75 kN，較設計條件略有減小。

由直股行車3種工況下輪軌動力附加力的變化規律可知：與尖軌降低值設計條件相比，尖軌降低值超限時輪軌動力附加力有顯著的增大，尤其是橫向動力附加力，增大幅度為7.0倍，垂向動力附加力的增大幅度達到3.5倍。尖軌降低值超限時，輪軌動力作用急劇惡化，加大轉轍器處鋼軌的傷損和磨耗速率，降低鋼軌使用壽命。鋼軌的傷損反過來加劇輪軌動力作用的惡化，形成惡性循環。尖軌降低值調整后，輪軌的動力附加力恢復到一個較小的水平，與設計條件相比則有所增大，說明調整尖軌降低值有效。

3.4 行車安全

尖軌降低值設計條件、降低值超限調整前及調整后3種工況下計算的車輪脫軌系數的變化規律見圖14。由圖14(a)可知：直股行車時，尖軌降低值設計條件下，車輪的脫軌系數幅值為0.10；尖軌降低值超限調整前，車輪的脫軌系數幅值為0.65，是設計條件下的6.5倍；尖軌降低值超限調整后，車輪的脫軌系數幅值為0.11，相比設計條件有所增大。由圖14(b)可知：側股行車時，尖軌降低值設計條件下，車輪的脫軌系數幅值為0.15；尖軌降低值超限調整前，車輪的脫軌系數幅值為0.18，是設計條件下的1.2倍；尖軌降低值超限調整后，車輪的脫軌系數幅值為0.14，比設計條件的略有減小。

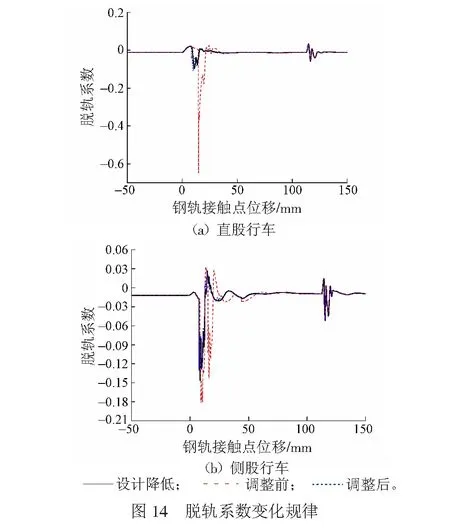
理論仿真尖軌降低值設計條件、降低值超限調整前及調整后3種工況下車輪減載率的變化規律見圖15。由圖15(a)可知：直股行車時，尖軌降低值設計條件下，車輪的減載率幅值為0.06；尖軌降低值超限調整前，車輪的減載率幅值為0.08，與設計條件的相差不大；尖軌降低值超限調整后，車輪的減載率幅值為0.14，較前兩種工況均有所增大，但數值相差不大。由圖15(b)可知：股行車時，設計尖軌降低值條件下，車輪的減載率幅值為0.05；尖軌降低值超限調整前，車輪的減載率幅值為0.03，與設計條件比較小但相差不大；尖軌降低值超限調整后，車輪的減載率幅值為0.04，與前兩種工況的相差不大。

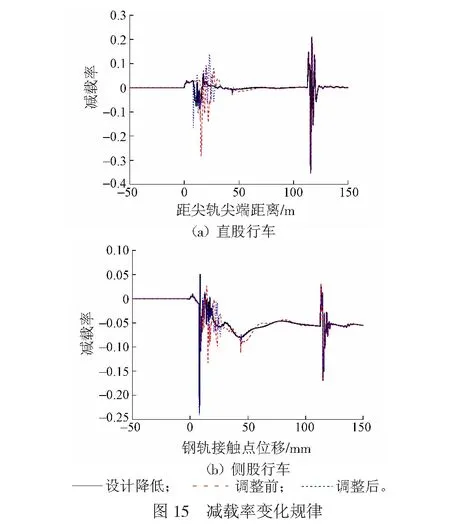
由直股行車3種工況下車輪脫軌系數和減載率的變化規律可知：相比尖軌降低值設計條件，尖軌降低值超限時，車輪脫軌系數顯著增大，脫軌系數達到0.65，已十分接近安全限值0.8，約為設計條件下的6.5倍;車輪減載率變化不大，說明尖軌降低值超限時，車輛通過轉轍器時，行車安全出現很大程度的惡化，嚴重時可能危及行車安全；尖軌降低值調整后，車輪脫軌系數與設計條件下相比變化不大，車輪減載率有所增大，說明調整尖軌降低值有效。

比較動車組車輛直股行車和側股行車時道岔轉轍器的動力響應，發現直股行車時尖軌降低值超限對道岔轉轍器動力特性的影響大于側股行車時的。主要原因有兩點：①動車組車輛直股行車的速度是295 km/h，遠大于側股行車的速度120 km/h；②道岔內不設置超高，因此動車組車輛側股行車時，由于道岔曲線線形的影響，離心運動在車輛的運動過程中起主要作用，此時尖軌降低值超限對道岔轉轍器動力響應帶來的影響不明顯。

4 結論

本文針對42號高速道岔尖軌降低值設計條件、超限調整前及調整后3種工況下，研究車輛通過時對道岔轉轍器動力特性的影響。主要結論如下：

(1) 與設計條件相比，尖軌降低值超限時道岔轉轍器輪載過渡段起點后移，加大了輪對通過轉轍器時蛇行運動的距離和幅度，加劇了輪對的擺動，最終導致輪軌動力作用惡化，影響行車。

(2) 直股行車時，與設計條件相比尖軌降低值超限、車輛通過道岔轉轍器處時，輪對橫向位移和車體橫向加速度均顯著增大，約為設計條件下的2倍，容易引起晃車現象，解釋了現場車輛通過該道岔轉轍器時存在的晃車現象。

(3) 直股行車時，與設計條件相比尖軌降低值超限時輪軌動力附加力顯著增大，尤其是橫向動力附加力增大幅度為7.0倍，垂向動力附加力的增大幅度約為3.5倍，輪軌動力作用的急劇增大，加大轉轍器處鋼軌的傷損速率，降低鋼軌使用壽命，鋼軌的傷損反過來加劇輪軌動力作用的惡化，形成惡性循環。

(4) 直股行車時，與設計條件相比尖軌降低值超限時車輪脫軌系數顯著增大，脫軌系數幅值達到0.65，十分接近安全限值0.8，約為設計條件下的6.5倍，車輪減載率變化不大。車輛通過轉轍器時，行車安全出現很大程度的惡化，嚴重時可能危及行車安全。

(5) 尖軌降低值出現超限時，道岔轉轍器的動力特性出現很大程度的惡化。調整后的道岔轉轍器動力特性與設計條件相差不大，說明尖軌降低值調整有效。

參考文獻：

[1〗 DUKKIPATI R V. Lateral Stability Analysis of a Railway Truck on Roller Rig[J〗. Mechanism and Machine Theory, 2001,36(2):189-204.

[2〗 王開云，劉鵬飛.車輛蛇形運動狀態下重載鐵路輪軌系統振動特性[J〗.工程力學，2012，29(1)：235-239.

WANG Kaiyun, LIU Pengfei. Characteristics of Dynamic Interaction Between Wheel and Rail due to the Hunting Montion on Heavy-haul Railway, 2012,29(1):235-239.

[3〗 王平.道岔轉轍器部分的力學特性分析[J〗.鐵道學報，2000，22(1)：79-82.

WANG Ping. Analysis of Mechanical Characteristic for Switch Proper of Turnout[J〗. Journal of The China Railway Society, 2000,22(1):79-82.

[4〗 王平.高速鐵路道岔設計理論與實踐[M〗.成都：西南交通大學出版社，2011：209-231.

[5〗 蔡小培，王平，李成輝.轉轍器軌距加寬對高速道岔動力特性的影響[J〗.鐵道科學與工程學報，2008，5(4)：1-6.

CAI Xiaopei, WANG Ping, LI Chenghui. Effect of Gauge Widening of Switch on Dynamic Characteristics of High-speed Turnout[J〗. Journal of Railway Science and Engineering, 2008,5(4):1-6.

[6〗 劉哲，王平，陳嶸，等.道岔動力參數設計法及其在轉轍器設計中的應用[J〗.西南交通大學學報，2012，47(4)：611-617.

LIU Zhe, WANG Ping, CHEN Rong,et al. Dynamic Parameters Design Method for Turnout and Its Application in Switch Design[J〗. Journal of Southwest Jiaotong University,2012,47(4):611-617.

[7〗 中華人民共和國鐵道部.TB/T3302—2003高速鐵路無砟軌道岔鋪設技術條件[S〗.北京：中國鐵道出版社，2003.

[8〗 曹陽.道岔平面線型動力分析及其設計方法研究[D〗.成都：西南交通大學，2013：33-64.

[9〗 陳小平.高速道岔軌道剛度理論及應用研究[D〗.成都: 西南交通大學，2008：36-46.

[10〗 陳果.車輛-軌道耦合系統隨機振動分析[D〗.成都：西南交通大學，2000：100-104.

[11〗 王開文.車輪接觸點跡線及輪軌接觸幾何參數的計算[J〗.西南交通大學學報，1984，19(1)：89-98.

WANG Kaiwen. The Track of Wheel Contact Points and the Calculation of Wheel/Rail Geometric Contact Parameters[J〗. Journal of Southwest Jiaotong University,1984,19(1):89-98.

[12〗 嚴雋髦.具有任意輪廓形狀的輪軌空間幾何約束的研究[J〗.西南交通大學學報，1983，18(3)：40-48.

YAN Juanmao. A Study on Wheel/Rail Spatial Geometric Constrains for Arbitrary Wheel and Rail Profiles[J〗. Journal of Southwest Jiaotong University, 1983,18(3):40-48.