不同頻率諧波下單芯電纜溫度場仿真分析

張 磊，朱立翔，陳青云

（1.國網(wǎng)湖北省電力公司宜昌供電公司，湖北 宜昌 443000；2.武漢黌門電工科技有限公司，湖北 武漢 430073）

0 引言

我國電力電纜線路在電力系統(tǒng)中的使用量正逐年上升，尤其是高壓交聯(lián)聚乙烯（XLPE）絕緣電纜在電網(wǎng)中所占的比重日益增長，城區(qū)110 kV線路大量采用交聯(lián)聚乙烯電纜[1-2]。隨著電力電子器件的增加，諧波對其影響越來越大。諧波頻率的不同，導線集膚效應和鄰近效應會導致電纜交流電阻、阻抗的不同，而且諧波頻率高，導線集膚效應和鄰近效應使諧波電阻較基波電阻增大，因此諧波引起的電阻損耗導致的電纜溫度升高問題不容忽略。

目前，從國內(nèi)外發(fā)表的文獻和著作來看，關于電力電纜溫度計算的研究多數(shù)采用解析方法，文獻[3-5]采用電纜熱模型來計算電纜的損耗值，不能實際模擬電纜的運行狀態(tài)，并且計算沒有考慮諧波的影響。而數(shù)值法具有運算靈活、拓寬研究范圍、減少實驗的工作量等優(yōu)點。

為了研究諧波下的電纜溫度，本文以電磁場理論為基礎，利用有限元數(shù)值計算，考慮趨膚效應和臨近效應，結(jié)合電纜的敷設方式，分析纜芯損耗、屏蔽層損耗及絕緣層損耗，基于多物理場耦合的方法模擬出諧波情況下電纜的溫度圖，定性分析了諧波對電纜溫度的影響，為電纜的熱老化壽命評估奠定了基礎。

1 電纜溫度場計算原理

本文使用大型數(shù)值仿真軟件Ansys作為電力電纜溫度場仿真計算的工具，采用有限元的方法進行電纜的溫度場建模與計算。本文研究對象為110 kV單芯電纜，電纜結(jié)構(gòu)如圖1所示。電纜的溫度與電纜的敷設方式和排列方式有著密切的關系。地下電力電纜的敷設根據(jù)安裝方式的不同分為：土壤直埋敷設、溝槽敷設和排管敷設。三相電力電纜在敷設時主要有兩種排列方法，分別是三角形排列和一字形排列。土壤直埋敷設是最常用的電力電纜安裝方式，本文以土壤直埋敷設方式下一字型排列的三相電纜為例進行仿真計算。

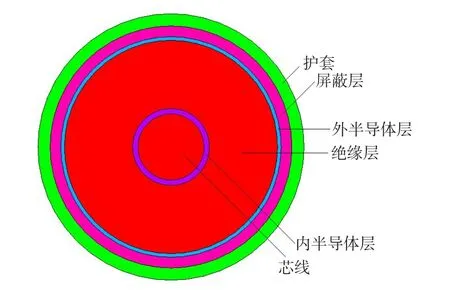
圖1 單芯電纜結(jié)構(gòu)圖Fig.1 The structure of single core cable

當電力電纜正常工作時，電纜產(chǎn)生的熱量在土壤中以固體傳熱的方式進行傳遞，這種傳熱方式為熱傳導，是指在物體內(nèi)部或相互接觸的物體表面之間，由于分子、原子及自由電子等微觀粒子的熱運動而產(chǎn)生的熱量傳遞現(xiàn)象，這是在固體內(nèi)的主要傳熱現(xiàn)象。當物體內(nèi)部的不同部位之間存在溫度差時，熱量將會以熱傳導的方式從溫度高的區(qū)域傳遞到溫度低的區(qū)域[6-9]。若定義單位時間內(nèi)流過單位面積的熱流量為熱流密度，用q表示，單位為 W/m2。熱流密度與垂直于傳熱方向的溫度變化率成正比，即

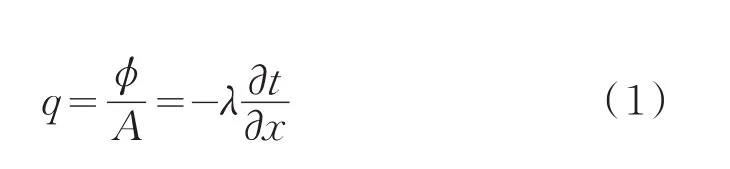
式中：φ表示通過面積A的總熱量，稱為熱流量，單位為W；比例系數(shù)λ為材料的導熱系數(shù)，單位為W/(m·K)。

由于電纜軸向長度非常大，一般認為軸向溫度分布均勻，因此本文只考慮電纜的徑向?qū)幔豢紤]三維軸向的導熱。其穩(wěn)態(tài)導熱微分方程如下式所示，通過熱源φ是否為0控制有無熱源。

在求解導熱微分方程時還需要已知邊界條件，才能準確求得唯一的溫度。導熱微分方程主要包括三種邊界條件[10-11]：

（1）第一類邊界條件：邊界溫度場恒定不變且為已知量

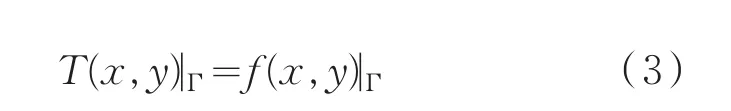
式中：G為物體邊界；T為已知溫度值。

（2）第二類邊界條件：研究場區(qū)邊界上的熱流密度分布已知

式中：k為導熱系數(shù)，單位為W/(m·℃)；q為已知熱流密度值，單位為W/m2。

（3）第三類邊界條件：研究區(qū)域邊界與周圍流體的表面?zhèn)鳠嵯禂?shù)以及周圍流體的溫度已知

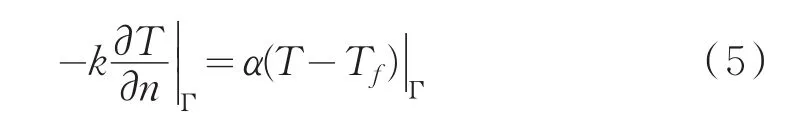
式中：a為對流換熱系數(shù)，單位為W/(m2·℃)；k為導熱系數(shù)，單位為W/(m·℃)。

2 電纜諧波損耗分析

諧波電流通過電纜時會使電力電纜在傳輸過程中產(chǎn)生有功損耗，散發(fā)出熱量，進而表現(xiàn)為電纜各層的溫度升高。電纜運行時，主要損耗分為電阻損耗與介質(zhì)損耗。電阻損耗又分為纜芯的電阻損耗和金屬屏蔽層的電阻損耗，而目前國內(nèi)外大多數(shù)都通過公式計算的方法來計算電纜的電阻損耗，常常忽略了金屬屏蔽層的損耗。本文通過有限元仿真的方法對絕緣層、纜芯、金屬屏蔽層各自損耗進行計算來求解電力電纜總的有功損耗。

2.1 絕緣層介質(zhì)損耗

電力電纜運行時在絕緣層上面會有比較高的電壓，由此而引發(fā)的電力電纜損耗稱為絕緣層損耗。對于普通單芯電力電纜，單位長度電纜的絕緣層損耗可以通過下式來計算，

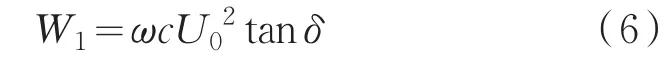
式中：ω為角頻率；U0為絕緣層對地相電壓，單位為 V；tanδ表示絕緣損耗因素，可以查表得到；c為單位長度的電纜的電容，單位 F/m。通過時諧電場的仿真來計算電纜絕緣層的介質(zhì)損耗。

2.2 纜芯損耗

電力電纜在通過交流電流時，纜芯的導體會發(fā)熱產(chǎn)生焦耳熱損耗，焦耳熱損耗可以通過下式求得，

式中：W2為電力電纜纜芯導體單位長度的損耗；I為電力電纜中通過的電流；R為電力電纜單位長度的有效電阻，Ω/m。計算電力電纜纜芯導體的交流電阻需要考慮電纜在運行時的趨膚效應和臨近效應，可以根據(jù)下式來計算，

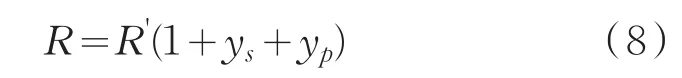
式中：yp為鄰近效應系數(shù)；ys為趨膚效應系數(shù)；R'為導體在工作溫度下的直流電阻。電纜在工作溫度下的直流電阻可以通過查表或者IEC-60287提供的公式計算得到[12-14]。在考慮趨膚效應和臨近效應的情況下通過時諧磁場仿真來計算電纜的纜芯損耗。

2.3 金屬屏蔽層損耗

電力電纜金屬屏蔽層中的熱損耗以兩種形式體現(xiàn)，分別為環(huán)流損耗和渦流損耗。在計算電力電纜金屬屏蔽層的損耗時，需要考慮電力電纜的導體芯數(shù)、排列方式、接地方式等因素。在工程實際應用中，為了減小金屬屏蔽層中產(chǎn)生的環(huán)流，主要采用金屬護套交叉互聯(lián)的接地方式。因此本文研究的110 kV單芯交聯(lián)聚乙烯電力電纜以交叉互聯(lián)的方式接地，不考慮金屬護套的環(huán)流，僅僅考慮由感應電壓產(chǎn)生的渦流損耗。同樣通過時諧磁場的仿真來計算金屬屏蔽層由于感應出渦流而產(chǎn)生的焦耳熱損耗。

3 電磁熱耦合分析

目前關于電力電纜溫度場的計算大多采用熱路模型的方法來計算，計算過程中所需的導線熱源是根據(jù)解析法進行計算得到的，作了比較多的假設和近似，如將該熱源值均勻加載到輸電線導體上求解電力電纜的溫度場分布。雖然在計算導體交流電阻公式中考慮了導體的集膚效應以及導體電導率的溫度(往往取導體最高允許溫度)特性，但公式中用到的許多參數(shù)值大多都是經(jīng)驗值等等。這些假設和近似就導致了現(xiàn)有的計算方法都存在不夠精確的缺點。因此，本文借鑒前人的研究成果，提出一種基于電磁-熱耦合場的數(shù)值計算方法，即溫度場計算所需熱源通過電磁場部分計算得到，形成一種比較符合實際的數(shù)值計算方法。

電磁熱耦合的方法同時考慮到了絕緣層損耗、纜芯損耗和屏蔽層損耗，并且也在計算中也考慮了導體之間的臨近效應及交流電流下導體的趨膚效應，能更準確的計算出電纜的各層損耗。該方法先用電場仿真計算出絕緣層的損耗，在金屬屏蔽層加載0電位，纜芯加載電壓激勵，計算得到絕緣層的電場分布，從而得到絕緣層的介質(zhì)損耗；再利用磁場仿真計算出纜芯和屏蔽層損耗，電纜電磁場的麥克斯韋方程為[15-18]

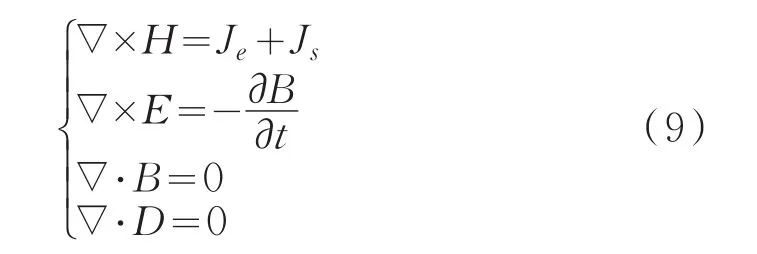
式中：Je為渦電流密度；Js為源電流密度。

不同介質(zhì)的交界面上電特性連續(xù)的方程為

式中n為法線方向上面的分量。

根據(jù)麥克斯韋方程，推導出電纜纜芯區(qū)域和金屬屏蔽層矢量磁位方程

式中：Js為電纜纜芯的電流密度；A1為電纜導體的矢量磁位；Je為金屬屏蔽層的渦流密度；A3為金屬護套的矢量磁位。

電纜各層損耗的計算公式為

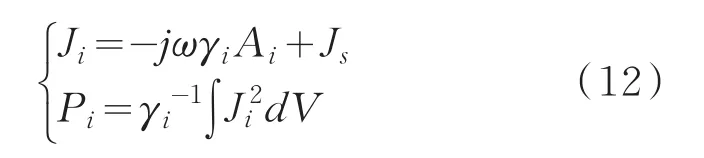
式中：Ji為各層電流密度；Ai為各層的矢量磁位；Pi為各層單位長度損耗功率；γi為材料的電導率。通過得到纜芯和金屬屏蔽層的電流密度，從而得到纜芯和屏蔽層損耗。

將三種損耗作為熱源導入到溫度場進行仿真計算出電纜各層的溫度及周圍土壤環(huán)境的溫度。與數(shù)值計算相比，有限元仿真的方法更準確地模擬了電纜的工作狀態(tài)，而且比利用經(jīng)驗公式計算電纜的各層損耗要更加精確，為研究各次諧波情況下電纜的溫升問題減小了誤差。電力電纜在各次諧波電流下的溫度計算流程圖如圖2所示。

圖2 電纜溫度計算流程圖Fig.2 The flow chart for calculating cable temperature

4 仿真分析

4.1 電纜模型及參數(shù)

根據(jù)圖2，可以通過編程對不同諧波情況下電纜溫度進行計算。對110 kV電纜進行各次諧波的仿真研究用的110 kV單芯XLPE電纜型號為YJLW03，電纜額定電壓為110 kV，標稱截面為1 000 mm2，電纜的截面圖如圖1所示，由內(nèi)而外分別是芯線、內(nèi)半導體層、絕緣層、外半導體層、屏蔽層和護套。電纜各層所用材料及尺寸參數(shù)如表1所示。線芯及金屬屏蔽層的電阻率是查資料所得，其它各層均可以作為絕緣材料來處理，電阻率取值均為1×1014Ω·m，該型號電纜各層均沒有非線性鐵磁材料，因此相對磁導率取值均為1。

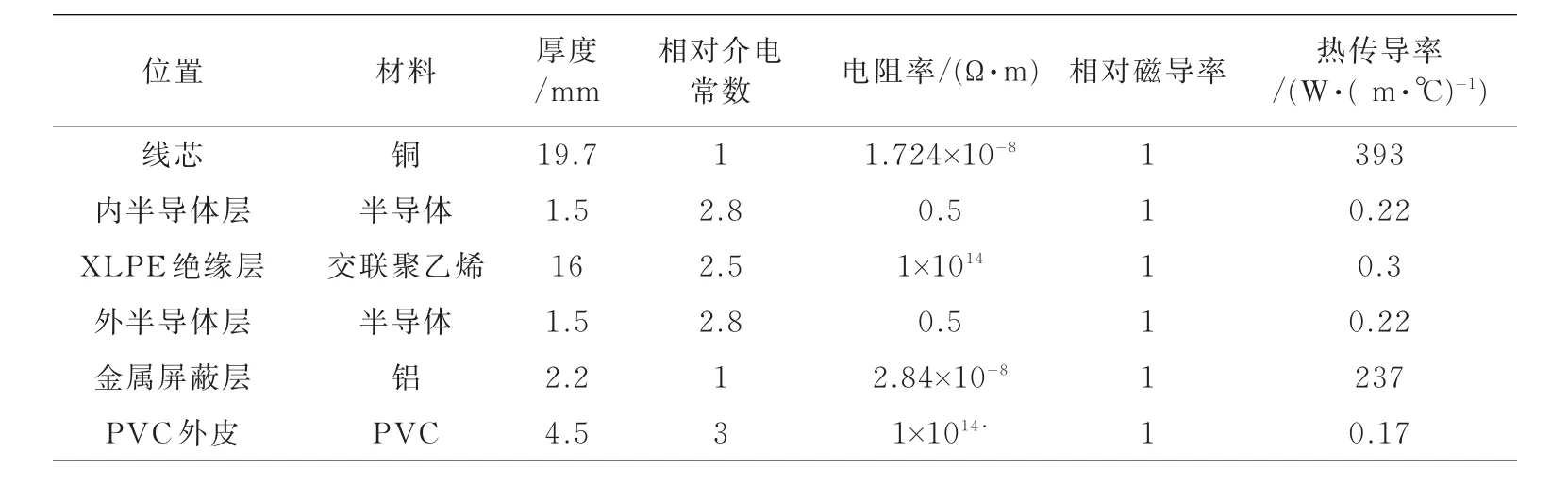
表1 電纜結(jié)構(gòu)參數(shù)Tab.1 The parameters of cable structure

以土壤直埋敷設方式下的一字型排列的三相電纜作為研究對象，三相電纜的土壤直埋敷設示意圖如圖3所示。電纜的上下側(cè)鋪以砂層，緊鄰砂層外側(cè)是保護板，保護板外面是土壤[19]。按照電纜之間的彼此間距為2 m，上保護板距離地面的深度為8 m，上下保護板間的距離為3 m，砂層或軟土對最近電纜的距離2 m，保護板的厚度0.8 m的參數(shù)進行三相電纜的敷設。周圍環(huán)境相關物理參數(shù)如表2所示。采用 FEM 計算電纜的溫度場分布，為提高計算效率，可將電纜的半無限大場轉(zhuǎn)換成閉域場，即確定計算區(qū)域的邊界，按有界場計算。結(jié)合相關文獻可知[20-22]：溫度僅在電纜附近變化較為劇烈，當遠離電纜時，土壤溫度將與環(huán)境溫度相同。通常距離電纜2 m的土壤已不受電纜的影響。因此可取距離下保護板2 m的土壤作為下邊界，取距離砂層外側(cè)2 m的土壤作為左右邊界。則土壤直埋敷設電纜的半無限大平面場可按有界場進行分析。對應的邊界條件為：下邊界條件為土壤溫度恒定值，符合第一類邊界條件；左右兩邊界條件的水平溫度梯度為 0，符合第二類邊界條件，即己知邊界法向熱流密度；地表邊界對流換熱系數(shù)和空氣溫度已知，符合第三類邊界條件。

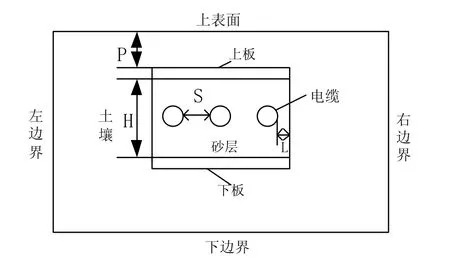
圖3 電纜三相直埋示意圖Fig.3 Three phase cable directly buried diagram

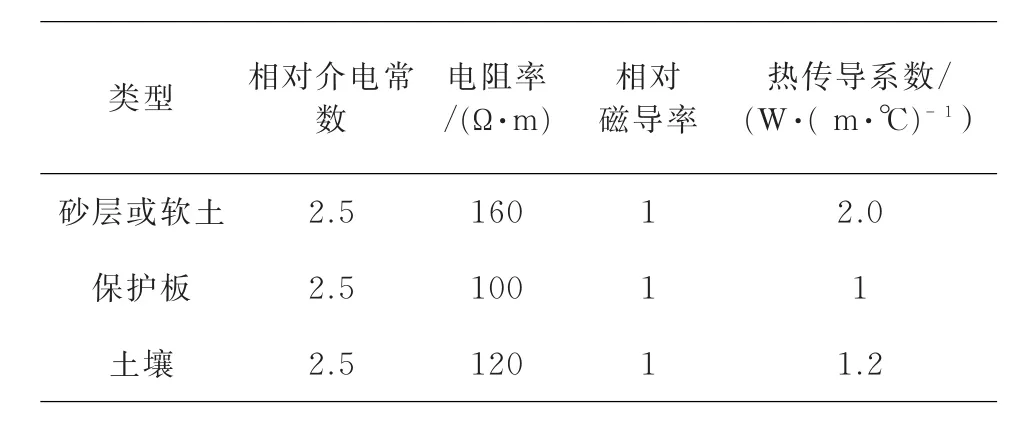
表2 周圍環(huán)境參數(shù)Tab.2 The environmental parameters

4.2 仿真結(jié)果分析

根據(jù)圖3所示電纜敷設示意圖，結(jié)合表1和表2中的參數(shù)在ansys中建立三相電纜的模型。模型建立之后進行網(wǎng)格的剖分，網(wǎng)格剖分的是否合理直接影響最后的計算結(jié)果，因此為了得到更準確的溫度，對于物理材料特性比較均勻的區(qū)域，如土壤區(qū)域，由于網(wǎng)格之間的方程與參數(shù)相同，網(wǎng)格剖分的相對而言會大一些；而對于電纜本體，材料的變化差異比較大，不同結(jié)構(gòu)層的厚度也比較小，采用映射剖分的方式進行剖分，且使用三角形網(wǎng)格，剖分比較密，以得到更加準確的結(jié)果。

首先以50 Hz基波為例加載進行仿真計算，查詢電纜手冊可知，所使用的電纜載流量為500 A，故磁場仿真中加載幅值為50 Hz的電流，電場仿真加載110 kV電壓，完成參數(shù)和邊界條件設置后，對模型進行仿真，按照第3節(jié)中的流程計算電纜的溫度。計算出基波情況下電纜的溫度場如圖4所示。電纜最高溫度為29.2℃。

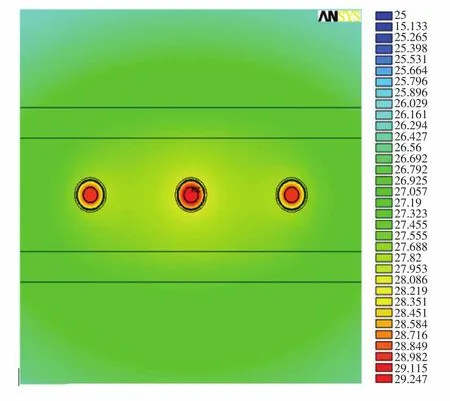
圖4 電纜溫度云圖（單位：℃）Fig.4 The cable temperature nephogram

分別對電纜進行磁場和電場的仿真，可以得到纜芯損耗、屏蔽層損耗以及絕緣層的介質(zhì)損耗。單根電纜的纜芯損耗和屏蔽層損耗密度圖如圖5所示，從圖5可以看出熱損耗在纜芯截面上呈非均勻分布，在纜芯表面附近達到最大值，這一分布與趨膚效應規(guī)律相吻合。單根電纜的介質(zhì)損耗密度圖如圖6所示，從圖6可以看出越靠近纜芯處的熱損耗越大。

圖5 單根電纜芯和屏蔽層損耗密度圖（單位：W/m）Fig.5 The loss density figure of single cable core and shield

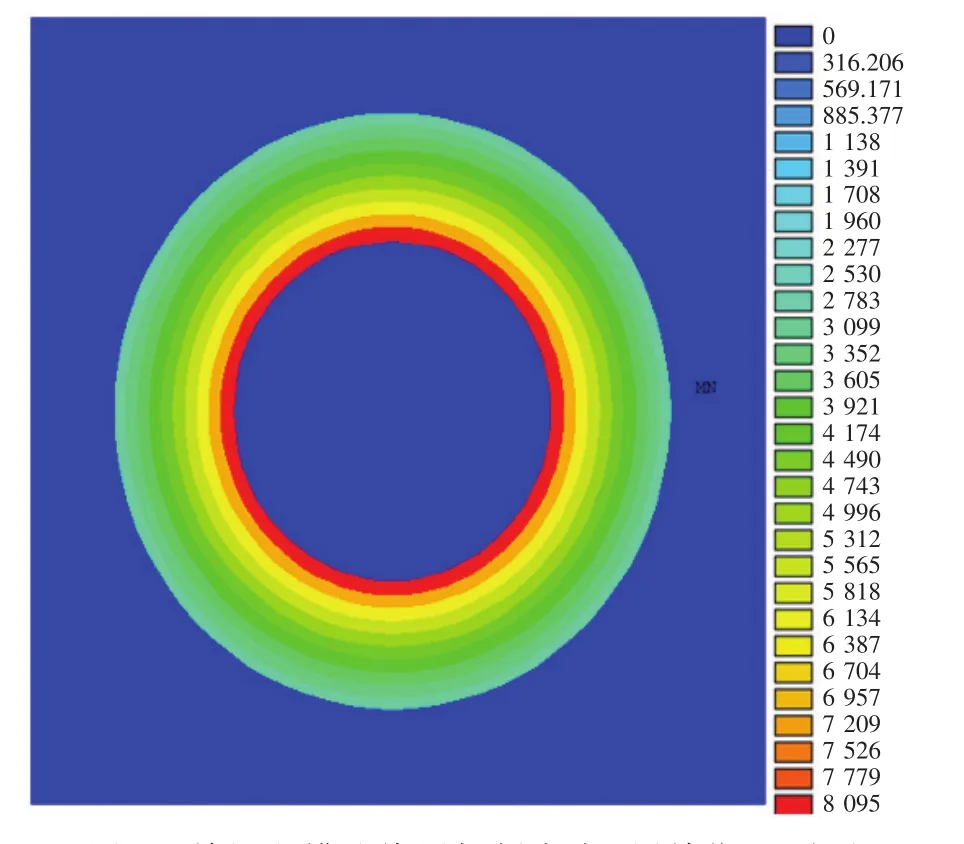
圖6 單根電纜絕緣層損耗密度圖（單位：W/m）Fig.6 The loss density figure of single cable insulation layer

按照同樣的方法分別對電纜加載不同頻率的諧波電流和電壓進行仿真分析，分別計算出不同頻率諧波下電纜的介質(zhì)損耗及渦流損耗，如圖7所示，頻率越高，渦流損耗越大，這是由于高次諧波下趨膚效應的作用更加明顯，電纜的等效電阻變大，因此損耗會增加，絕緣層介質(zhì)損耗也會增加，但相對而言，介質(zhì)損耗增加程度比電阻損耗小得多，說明高次諧波對趨膚效應的影響更加顯著。

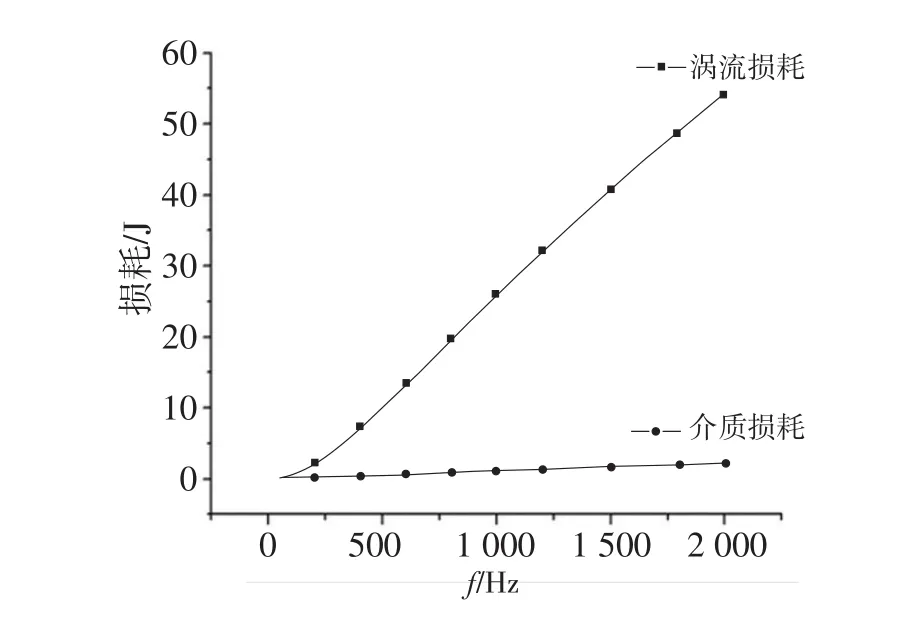
圖7 頻率對介質(zhì)損耗和渦流損耗的影響Fig.7 The influence of frequency on the dielectric loss and eddy current loss

不同頻率諧波下電纜溫度變化如圖8所示，在低頻下，諧波對電纜溫度影響不大，但是隨著諧波頻率的增加，高次諧波下，電纜的最高溫度會顯著上升。表面高次諧波對電纜溫升有極大影響，會加速電纜的老化。

圖8 電纜溫度隨頻率變化圖Fig.8 The cable temperature on frequency variation

5 結(jié)論

（1）分析了電力電纜的溫度場計算原理，以及電纜焦耳熱損耗的計算方法，電纜損耗包括絕緣層損耗、纜芯損耗和屏蔽層損耗，計算電纜的損耗需要考慮趨膚效應和臨近效應，為后面的多物理場耦合模型提供了理論依據(jù)。

（2）建立了一種比較符合實際的電力電纜線路的電磁-熱耦合模型，形成了多物理耦合場的有限元法的電力電纜輸電線路在諧波下的溫度計算方法。

（3）以土壤直埋敷設的110 kV單芯三相電纜為實例進行數(shù)值計算與分析。結(jié)果表明熱損耗在纜芯截面上呈非均勻分布，在纜芯表面附近達到最大值，這一電流分布與趨膚效應規(guī)律相吻合，從而驗證了模型和計算的正確性。

[參考文獻]（References）

[1]李紅雷，張麗，李莉華.交聯(lián)聚乙烯電纜在線監(jiān)測與檢測[J].中國電力，2010，43(12)：31-34.LI Honglei,ZHANG Li,LI Lihua.Online monitor?ing and detection techniques of XLPE cables[J].Electric Power,2010,3(12)：31-34.

[2]曹曉瓏，劉英，鐘力生，等.從2010國際大電網(wǎng)會議看電力電纜技術的發(fā)展現(xiàn)狀和趨勢[J].高電壓技術，2010，36(12)：3078-3083.CAO Xiaolong,LIU Ying,ZHONG Lisheng,et al.Power Cable Technology Status and trends seeing from the 2010 CIGRE conference[J].High Voltage Engineering,2010,36(12)：3078-3083.

[3]Olsen R S.Dynamic temperature estimation and real time emergency rating of transmission cables[C]//2012 IEEE Power and Energy Society General Meet?ing,2012.

[4]Olsen，Rasums.Modelling of dynamic transmission cable temperature considering soil-specific heat，thermal resistivity，and precipitation[J].IEEE Trans?actions on Power Delivery,2013,28(3)：1909-1917.

[5]陳誠.電纜溝敷設10 kV三芯電纜溫度場計算及試驗研究[D].廣州：華南理工大學，2012.CHEN Cheng.The Computational and Experimental Rese-arch on 10 kV Three-core Cable Temperature Field of the Cable Trench[D].Guangzhou：South Chi?na University Technology,2012.

[6]劉毅剛,羅俊華.電纜導體溫度實時計算的數(shù)學方法[J].高電壓技術，2005，31(5)：52-54.LIU Yigang,LUO Junhua.Mathematical method of temperature calculation of power cable conductor in real time[J].High Voltage Engineering,2005,31(5)：52-54.

[7]趙建華,袁宏水,范維澄,等.基于表面溫度場的電纜線芯溫度在線診斷研究[J].中國電機工程學報,1999，19(11)：52-54.ZHAO Jianhua,YUAN Hongyong,FAN Weicheng,et al.Surface temperature field based online diagno?ses study for power cable's conductor temperature[J].Proceedings of the CSEE,1999,19(11)：52-54.

[8]梁永春,李延沐,李彥明,等.利用模擬熱荷法計算地下電纜穩(wěn)態(tài)溫度場[J].中國電機工程學報，2008，28(16)：129-134.LIANG Yongchun,LI Yanmu,LI Yanming,et al.Calculation of the static temperature field of under?ground cables u sing heat charge simulation method[J].Proceedings of the CSEE,2008,28(16)：129-134.

[9]李志堅,張東斐,曹慧玲,等.地下埋設電纜溫度場和載流量的數(shù)值計算[J].高電壓技術，2004，30(4)：27-30.LI Zhijian,ZHANG Dongfei,CAO Huiling,et al.Numerical calculation of temperature field and cur?rent of underground cable[J].High Voltage Engineer?ing,2004,30(4)：27-30.

茄子棉鈴蟲主要啃食茄子莖及嫩芽，嚴重影響茄子的正常生長，及時進行防治。以幼蟲蛀食蕾、花、果為主，也危害嫩莖、葉和芽。花蕾受害時，苞葉張開，變成黃綠色，2～3天后脫落。幼果常被吃空或引起腐爛而脫落，成果雖然只被蛀食部分果肉，但因蛀孔在蒂部，便于雨水、病菌流入引起腐爛，所以，果實大量被蛀會導致果實腐爛脫落，造成減產(chǎn)。

[10]王有元，陳仁剛，陳偉根，等.有限元法計算地下電纜穩(wěn)態(tài)溫度場及其影響因素[J].高電壓技術，2008，34（12）：3086-3092.WANG Youyuan,CHEN Rengang,CHEN Weigen,et al.Calculation of static temperature field of bur?ied cable based on FEM and analysis of influential factors[J].High Voltage Engineering,2008，34（12）：3086-3092.

[11]梁永春，李彥明，柴進愛.地下電纜群穩(wěn)態(tài)溫度場和載流量計算新方法[J].電工技術學報，2007，22（8）：185-190.LIANG Yongchun,LI Yanming,CHAI Jin’ai.A new method to calculate the steady-state tempera?ture field and ampacity of underground cable sys?tem[J].Transactions of China Electrotechnical Soci?ety,2007,22(8)：185-190.

[12]IEC 602872321—1995 Calculation of the current rating of electric cables，part 3：Sections on oper?ating conditions,section 1：Reference operating conditions and selection of cable type[S].1995.

[13]IEC 602872121—1994 Calculation of the current rating of electric cables，part 1：Current rating equations(100% load factor)and calculation of losses,section 1：General[S].1994.

[14]IEC 602872122—1993 Calculation of the current rating of electric cables part 1：Current rating equations(100% load factor)and calculation of losses，section 2：Sheath eddy current loss factor for two circuit s in flat formation[S].1993.

[15]胡明麗.基于多物理場耦合模型的高壓電力電纜溫度場與載流量計算[D].廣州：華南理工大學，2015.HU Mingli.Calculation of thermal distribution and ampacity for high-voltage power cables by using multi-physics coupled model[D]. Guangzhou：South China University of Technology,2015.

[16]孫國霞，舒乃秋，吳曉文，等.基于多物理場耦合的氣體絕緣母線觸頭接觸溫升有限元計算[J].電工技術學報，2013，28（2）：408-413.SUN Guoxia,SHU Naiqiu,WU Xiaowen,et al.Fi?nite element analysis of contact temperature rise in gas insulated busbars based on coupled multi-physics[J].TransactionsofChinaElectro?technical Society,2013,28(2)：408-413.

[17]楊上興.基于電磁－熱耦合模型的直埋電纜載流量計算及間距的影響研究[J].電氣應用，2015，34（19）：85-89.YANG Shangxing.Study on the effect of load flow calculation and spacing of buried cables based on electromagnetic thermal coupling model[J].Electro?technical Application,2015,34(19)：85-89.

[18]邱超.雙回路單芯電力電纜不同敷設與排列方式下溫度場與載流量計算[D].廣州：華南理工大學，2013.QIU Chao.Calculations of thermal field and ampac?ity for two-circuit single-core power cables in dif?ferent laying modes and arrangements[D].Guang?zhou：South China University of Technology,2013.

[19]DL/T5221-2005城市電力電纜項目設計技術規(guī)定，2005.DL/T5221-2005 Technical rule for design of urban power cables，2005.

[20]孔祥謙.有限單元法在傳熱學中的應用[M].3版.北京：科學技術出版社，1998.KONG Xiangqian.ApplicationofFEM inheat transfer[M].3rd ed.Beijing：Science Press,1998.

[21]陶文銓.數(shù)值傳熱學[M].2版.西安：西安交通大學出版社，2001.TAO Wenquan.Numerical heat transfer[M].2nd ed.Xi’an：Xi’an Jiaotong University Press,2001.

[22]梁永春，柴進愛，李彥明，等.有限元法計算交聯(lián)電纜渦流損耗[J].高電壓技術，2007，33（9）：196-199.LIANG Yongchun,CHAI Jin’ai,LI Yanming,et al.Calculation of eddy current losses in XLPE cables by FEM[J].High Voltage Engineering,2007，33(9)：196-199.