懷疑邏輯的弗協(xié)調(diào)方案探賾

周龍生

(北京大學(xué) 哲學(xué)系，北京　100871)

?

懷疑邏輯的弗協(xié)調(diào)方案探賾

周龍生

(北京大學(xué) 哲學(xué)系，北京100871)

摘要：目的 提供一個(gè)建立在弗協(xié)調(diào)認(rèn)知邏輯基礎(chǔ)上的包含三分認(rèn)知世界思想的懷疑邏輯構(gòu)造方案。方法 在系統(tǒng)SPN內(nèi)定義相關(guān)的認(rèn)知模態(tài)算子。結(jié)果 懷疑邏輯三分認(rèn)知世界的設(shè)想得以實(shí)現(xiàn)，同時(shí)由于弗協(xié)調(diào)認(rèn)知邏輯的原因，一些懷疑邏輯公式的有效性發(fā)生了變化。

關(guān)鍵詞：懷疑邏輯；三分認(rèn)知世界；弗協(xié)調(diào)認(rèn)知邏輯

一、懷疑邏輯與三分認(rèn)知世界

人們?cè)谠S多領(lǐng)域要運(yùn)用關(guān)于懷疑的推理。懷疑邏輯的提出對(duì)于懷疑這一認(rèn)知模態(tài)詞作邏輯分析提供了可能。關(guān)于懷疑算子的性質(zhì)是通過(guò)一系列懷疑公理[1]的設(shè)想來(lái)刻畫(huà)的。如下所示，其中懷疑算子用“D”表示。

D2:Dq→D(p→q) ∨Dp

D4:D(p∨q)→Dp∧Dq

D5:D(p∧q)→Dp∨Dq

其中公理D8被稱(chēng)為“笛卡爾公理”，即如果懷疑p，那么對(duì)懷疑p是不可懷疑的。笛卡爾的名言“我思，故我在”在此可理解為：我懷疑，但我當(dāng)下的懷疑是不可懷疑的。“公理D8為‘我思，故我在’的形式化。”[1]

“人的認(rèn)知世界可劃分為三個(gè)部分：信念世界(WB)、懷疑世界(WD)和無(wú)知世界(WU)。這三個(gè)世界是命題組成的集合，組成它們的元素是認(rèn)知命題。”[2]

信念世界是指某人所相信的命題所組成的世界，即信念組成的集合。某個(gè)命題p屬于信念世界，記作Bp。懷疑世界是由認(rèn)知主體懷疑的那些命題組成的。某個(gè)命題p是懷疑世界的一個(gè)元素記為Dp。無(wú)知世界“是由那些主體沒(méi)有‘考慮’的命題所構(gòu)成。對(duì)于這些命題(以及它們的否定)，認(rèn)知主體從沒(méi)有‘接觸’到它們，主體對(duì)它們一無(wú)所知，或者主體雖然‘接觸’過(guò)它們，但不清楚它們的意義，因而主體既不相信它們，也不懷疑它們”[2]。主體對(duì)p無(wú)知，記為Up。3個(gè)認(rèn)知世界之間的關(guān)系是：信念世界(WB)、懷疑世界(WD)和無(wú)知世界(WU)共同組成整個(gè)認(rèn)知世界，并且這3個(gè)世界不會(huì)相互重疊。三者的關(guān)系如圖1所示。

圖1　設(shè)想中的認(rèn)知世界關(guān)系

二、弗協(xié)調(diào)認(rèn)知邏輯SPN

定義(LPN)弗協(xié)調(diào)認(rèn)知邏輯SPN使用的形式語(yǔ)言L(fǎng)PN,是由弗協(xié)調(diào)命題邏輯的語(yǔ)言加認(rèn)知算子※得到的。LPN包括4類(lèi)初始符號(hào)：

[1] 命題符：p1，p2，p3，…，pk，…；k為自然數(shù)；

[3] 認(rèn)知聯(lián)結(jié)符：※；

[4] 標(biāo)點(diǎn)符：(，)。

定義(Expr(LPN))一個(gè)由形式語(yǔ)言L(fǎng)PN中符號(hào)構(gòu)成的任意有窮序列稱(chēng)為一個(gè)表達(dá)式，全體表達(dá)式組成的集合記為Expr(LPN)。

定義(Atom(LPN))A∈Atom(LPN)，即LPN中的一個(gè)表達(dá)式A是原子公式，當(dāng)且僅當(dāng)A是一個(gè)單獨(dú)的命題符。

定義(Form(LPN))A∈Form(LPN)，即LPN中的一個(gè)表達(dá)式A是公式，當(dāng)且僅當(dāng)它能由(有窮次使用)下列規(guī)則得到：

[1] Atom(LPN) ?Form (LPN)，即原子公式是公式；

[3] 如果A，B∈Form(LPN)，則(A∧B)，(A∨B)，(A→B)∈Form(LPN)。

為敘述方便，引進(jìn)以下縮寫(xiě)符號(hào)：

(A?B)是指(A→B)∧(B→A)；

Ak指A00…0，這里一共有k個(gè)0，其中k為自然數(shù)；

A(n)指(…(A1∧ A2) ∧ A3∧…∧An)；

弗協(xié)調(diào)認(rèn)知邏輯的公理系統(tǒng)是在科斯塔的弗協(xié)調(diào)命題邏輯系統(tǒng)Cn(1≤n<ω)上增加含認(rèn)知算子※的若干公理以及新的推理規(guī)則構(gòu)成。公理模式如下：

(Ax1)至(Ax12)所有Cn(1≤n<ω)的公理模式[3]

(Ax13) A(n)→(※A)(n)

(Ax14) ※(A→B) →(※A→※B)

(Ax15) ※A→A

分離規(guī)則(MP)：如果├A，├A→B，那么├B；

認(rèn)知規(guī)則(N)：如果├A，那么├※A。

定義(框架、SPN框架)設(shè)〈W，R〉是任一二元組，〈W，R〉是一個(gè)正規(guī)框架(簡(jiǎn)稱(chēng)框架)，當(dāng)且僅當(dāng)，W是任一非空集，R是W上的任一二元關(guān)系，即R?W×W。

一個(gè)SPN框架，表示為FSPN，是同時(shí)滿(mǎn)足下述條件的一個(gè)框架〈W，R〉，對(duì)于所有的w∈W，

[1] ?w(Rww)；

[2] ?w?w′?w′′ (Rww′∧ Rw′w″→Rww″)。

定義(賦值)設(shè)〈W，R〉是任一框架，V是〈W，R〉上對(duì)LPN公式的一個(gè)賦值，當(dāng)且僅當(dāng)，V是LPN公式集Form(LPN)與W的笛卡爾積Form(LPN) ×W到集合{1，0}上的映射，即

V： Form(LPN)×W → {1，0}

通過(guò)分析及居民生態(tài)城市和城市林業(yè)的內(nèi)涵和特點(diǎn)，宣傳在構(gòu)建生態(tài)城市建設(shè)中發(fā)展城市林業(yè)的作用，提出推進(jìn)城市林業(yè)和生態(tài)城市可持續(xù)發(fā)展的建議，充分發(fā)揮城市林業(yè)在構(gòu)建生態(tài)城市中的作用。讓每一位公民參與到建設(shè)生態(tài)城市的工程中，全力打造一個(gè)生態(tài)良好的發(fā)展中城市，為我國(guó)生態(tài)環(huán)境的改善及生態(tài)經(jīng)濟(jì)的發(fā)展貢獻(xiàn)力量。

并滿(mǎn)足以下條件：對(duì)任意的LPN公式A、B，任意的w∈W，

[4] V(A→B，w)=1 ? V(A，w)=0或者V(B，w)=1；

[5] V(A∧B，w)=1 ? V(A，w)=V(B，w)=1；

[6] V(A∨B，w)=1 ? V(A，w)=1或者V(B，w)=1；

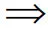
[8] V(※A，w)=1 ? 對(duì)于任一w′ ∈W，若Rww′，則V(A，w′)=1。

定理如果V是框架F上的一個(gè)賦值，那么對(duì)任意的A∈Form(LPN)，w∈W：

[3] V(A，w)=0 ? V(～A，w)=1；

[6] V(※※A，w)=1 ? 對(duì)于任意的w，w′，w″∈W，如果Rww′并且Rw′w″，則V(A，w″)=1。

弗協(xié)調(diào)認(rèn)知邏輯系統(tǒng)SPN具有可靠性和完備性。相關(guān)證明參見(jiàn)張清宇的《弗協(xié)調(diào)邏輯》[4]。

三、SPN與三分認(rèn)知世界

表1　真值組合1

表2　真值組合2

由表1可知，我們定義“相信”和“懷疑”這兩個(gè)算子時(shí)，如果采取如下方法：

則公式Bp∧Dp是可滿(mǎn)足的，即存在某個(gè)認(rèn)知狀態(tài)w∈W，使得V(Bp∧Dp，w)=1，也就是說(shuō)在某個(gè)認(rèn)知狀態(tài)w中有命題p既屬于信念世界WB，又屬于懷疑世界WD。并且可以看出，對(duì)于任何w∈W，都有V(Bp∨Dp，w)=1成立，即在狀態(tài)w中不存在既不屬于信念世界WB又不屬于懷疑世界WD的認(rèn)知命題。這樣構(gòu)成的認(rèn)知狀態(tài)中，無(wú)知世界WU變?yōu)榭占恕Ｈ鐖D2所示。

圖2　SPN中的一種認(rèn)知世界關(guān)系

其中W=WB∪WD，陰影部分顯示的是滿(mǎn)足Bp∧Dp的認(rèn)知命題集合。這樣的定義與懷疑邏輯的本意和三分認(rèn)知世界的思想相去甚遠(yuǎn)。

表3　真值組合3

表4　真值組合4

于是，我們得到如下定義：

從得出定義的過(guò)程來(lái)看，滿(mǎn)足Up的認(rèn)知命題集，不會(huì)和滿(mǎn)足Bp或者滿(mǎn)足Dp的命題集相交，即不存在既屬于信念世界又屬于無(wú)知世界，或者既屬于懷疑世界又屬于無(wú)知世界的認(rèn)知命題。

以上3組定義的生成和語(yǔ)義證明的過(guò)程可以用下面關(guān)系圖表示：

表4列出了各認(rèn)知命題間所有可能的真值關(guān)系。因此，對(duì)于所有的認(rèn)知命題而言，要么滿(mǎn)足公式Bp，要么滿(mǎn)足公式Dp，要么滿(mǎn)足公式Up；由這些認(rèn)知命題構(gòu)成的與之相應(yīng)的信念世界、懷疑世界以及無(wú)知世界構(gòu)成了全部的認(rèn)知世界。

至此，我們?cè)诟f(xié)調(diào)認(rèn)知邏輯系統(tǒng)SPN內(nèi)對(duì)于相關(guān)認(rèn)知算子的定義，以及隨之確定的3組命題集合，體現(xiàn)了三分認(rèn)知世界的思想，保證了3個(gè)世界的性質(zhì)與關(guān)系得到實(shí)現(xiàn)。

即兩個(gè)互相矛盾的命題可以同時(shí)成為我們的信念。這樣的結(jié)果在三分認(rèn)知世界理論的最初設(shè)想中是不存在的，之所以得到這樣的結(jié)果，是因?yàn)楦f(xié)調(diào)方案所致。

四、SPN與懷疑邏輯

以下是一些懷疑邏輯的SPN系統(tǒng)內(nèi)定理：

SPND1: Dq→D(p→q)∨Dp

SPND3: D(p∨q)→Dp∧Dq

SPND4: D(p∧q)→Dp∨Dq

SPND6: D(p∧～p)

SPND7: ～Dp→～D～Dp

SPND9: Dq∧～Dp→D(p→q)

例1：D(p∧～p)是系統(tǒng)內(nèi)定理

證明：

1. ※p→p

2.～p→～※p

3. ～～p→～※～p

4.p→～※～p

5.※p→～※～p

6.※～p→～※p

7.※～(p∧～p)→～※(p∧～p)

8. ～(p∧～p)

9. ※～(p∧～p)

10. ～※(p∧～p)

11.D(p∧～p)

例3：Dp→～DDp(笛卡爾公理)不是SPN系統(tǒng)內(nèi)定理。

Dp→～DDp存在SPN框架上的反模型，如下所示。

笛卡爾公理Dp→～DDp在SPN系統(tǒng)內(nèi)的失效，說(shuō)明了笛卡爾公理對(duì)于SPN系統(tǒng)的獨(dú)立性，也說(shuō)明了笛卡爾公理和其他的懷疑邏輯公理在刻畫(huà)關(guān)于“懷疑”認(rèn)知模態(tài)詞的性質(zhì)上的層次差異。然而，我們可以在SPN的基礎(chǔ)上，將笛卡爾公理Dp→～DDp作為新的系統(tǒng)公理引入，構(gòu)建新的形式系統(tǒng)。或者增加一條可以推演出笛卡爾公理的系統(tǒng)公理，例如：

(Ax17) ～※～A→※～※～A，

得到新系統(tǒng)SPN*，則笛卡爾公理Dp→～DDp在SPN*內(nèi)是可證的。

證明：

1. ～※～～p→※～※～～p

2.※～※～～p→ ～～※～※～～p

3. ～※～～p→ ～～※～※～～p

4. ～※p→ ～～※～※p

5.Dp→～DDp

參考文獻(xiàn)：

[1]潘天群.建立在“笛卡爾公理”上的一個(gè)懷疑邏輯系統(tǒng)[J].湖南科技大學(xué)學(xué)報(bào)(社會(huì)科學(xué)版),2004(9):33-36.

[2]潘天群.三分的認(rèn)知世界與懷疑邏輯的獨(dú)立性[J].湖南科技大學(xué)學(xué)報(bào)(社會(huì)科學(xué)版),2005(9):39-41.

[3]杜國(guó)平.經(jīng)典邏輯與非經(jīng)典邏輯基礎(chǔ)[M].北京：高等教育出版社,2006.

[4]張清宇.弗協(xié)調(diào)邏輯[M].北京：中國(guó)社會(huì)出版社,2003.

[5]周北海.模態(tài)邏輯導(dǎo)論[M].北京：北京大學(xué)出版社,1997.

(責(zé)任編輯張佑法)

Preliminary Analysis of Paraconsistent Doubting Logic

ZHOU Long-sheng

(Department of Philosophy, Peking University, Beijing 100871, China)

Abstract:Objective This paper aimed to provide a formalization of doubting logic with tri-partitioning of epistemic worlds based on paraconsistent epistemic logic. Method We defined the related epistemic modal operator in SPN. Result The idea of tri-partitioning of epistemic worlds was achieved. Meanwhile, the validity of some formulas about doubting logic was changed for the paraconsistent epistemic logic reasons.

Key words:doubting logic; tri-partitioning of epistemic world; paraconsistent epistemic logic

中圖分類(lèi)號(hào)：B81

文獻(xiàn)標(biāo)識(shí)碼：A

文章編號(hào)：1674-8425(2016)03-0025-06

作者簡(jiǎn)介：周龍生(1981—)，男，山東棗莊人，博士研究生，研究方向：符號(hào)邏輯。

基金項(xiàng)目：國(guó)家社會(huì)科學(xué)基金重大項(xiàng)目“應(yīng)用邏輯與邏輯應(yīng)用研究”(14ZDB014)

收稿日期：2015-08-09

doi:10.3969/j.issn.1674-8425(s).2016.03.005

引用格式：周龍生.懷疑邏輯的弗協(xié)調(diào)方案探賾[J].重慶理工大學(xué)學(xué)報(bào)(社會(huì)科學(xué))，2016(3):25-30.

Citation format：ZHOU Long-sheng.Preliminary Analysis of Paraconsistent Doubting Logic[J].Journal of Chongqing University of Technology(Social Science)，2016(3):25-30.