基于頻響函數辨識鼓筒-輪盤結合部連接參數的選點原則

王洪玉， 秦朝燁， 褚福磊， 劉彥琦(.清華大學 摩擦學國家重點實驗室，北京　00084； . 北京市勞動保護科學研究所，北京　00054)

?

基于頻響函數辨識鼓筒-輪盤結合部連接參數的選點原則

王洪玉1， 秦朝燁1， 褚福磊1， 劉彥琦2(1.清華大學 摩擦學國家重點實驗室，北京100084； 2. 北京市勞動保護科學研究所，北京100054)

摘要：基于頻響函數的辨識方法被廣泛用于識別結合部動態參數，其中如何選擇頻響數據是關鍵問題。針對結合部采用彈簧和阻尼器連接的鼓筒-輪盤模型提出了頻響數據選取原則和對應于該原則的量化標準。具體選點原則為所選取的局部信噪比最高的頻點所對應的模態對連接剛度的綜合靈敏度應該最高。為了定量比較不同模態對連接剛度的綜合靈敏度，建立了具體的量化指標和標準。理論分析表明所提出的頻響數據選取原則和量化標準是有效的，具有一定的工程應用價值。

關鍵詞：連接結合部；頻響函數；參數識別；選點原則；量化指標

盤鼓式轉子結構廣泛應用于航空發動機等大型渦輪機械中。盤鼓式轉子由輪盤、鼓筒和轉軸組成，各級輪盤和鼓筒之間主要通過螺栓連接在一起。相關研究表明，連接結合部對機械系統的整體動力學特性具有非常重要的影響[1]。由于影響結合部剛度、阻尼特性的因素眾多[2]，作用機理異常復雜，純粹依靠理論方法精確獲得結合部特性參數顯得非常困難[3]。因此，目前結合部連接參數的獲取主要依賴參數辨識的方法。

連接結合部參數辨識的方法主要有兩種，一是基于模型的辨識方法[4-6]，二是基于實驗的辨識方法[7-9]。基于模型的辨識方法主要是同時利用結構有限元模型和實驗數據辨識結合部參數。Yuan等[4-5]利用減縮的有限元模型和不完整模態振型辨識結合部的剛度和阻尼。Yang等[6]將不完備頻響函數與子結構有限元模型相結合辨識栓接結合部連接參數。基于模型的辨識方法，其缺點是結構的阻尼特性無法通過有限元方法獲得。基于實驗的辨識方法主要是利用實測頻響函數識別結合部的等效參數。Hwang[7]利用含有結合部和不含結合部兩種條件下的頻響函數逆矩陣辨識得到了結合部參數。Yang等[8]利用實測頻響函數辨識出了栓接結合部的平移剛度和扭轉剛度。Wang等[9]針對栓接結合部剛度與阻尼量級相差顯著的情況，提出應用誤差函數選擇最佳數據辨識結合部參數。蔡力鋼等[10-11]針對頻響函數完備和不完備的情況，研究了結合部等效動力學參數的辨識問題。

盡管基于頻響函數的識別方法應用廣泛，然而如何選擇有效的頻響數據以確保結合部參數辨識的精度與效率一直未能得到有效解決。李玲等[12]提出采用條件數的方法對實測頻響數據進行處理，然后進行結合部參數辨識，然而沒有明確定義保證矩陣為良態的臨界條件數。本文從概率靈敏度的角度出發，針對結合部采用彈簧和阻尼器連接的鼓筒-輪盤模型，提出了頻響數據選取原則和具體的量化標準。

1鼓筒-輪盤模型

如圖1所示為鼓筒-輪盤結構力學模型，模型中左端輪盤與右端鼓筒之間通過4個連接單元連接在一起，左端鼓筒端面固支。如圖2所示，每個連接單元由3個正交方向的等效彈簧和等效阻尼器構成，r,θ,z分別表示徑向、周向和軸向。軸向連接剛度和阻尼的取值根據文獻[13]確定，徑向和軸向連接參數的取值根據文獻[14]確定，如表1所示。

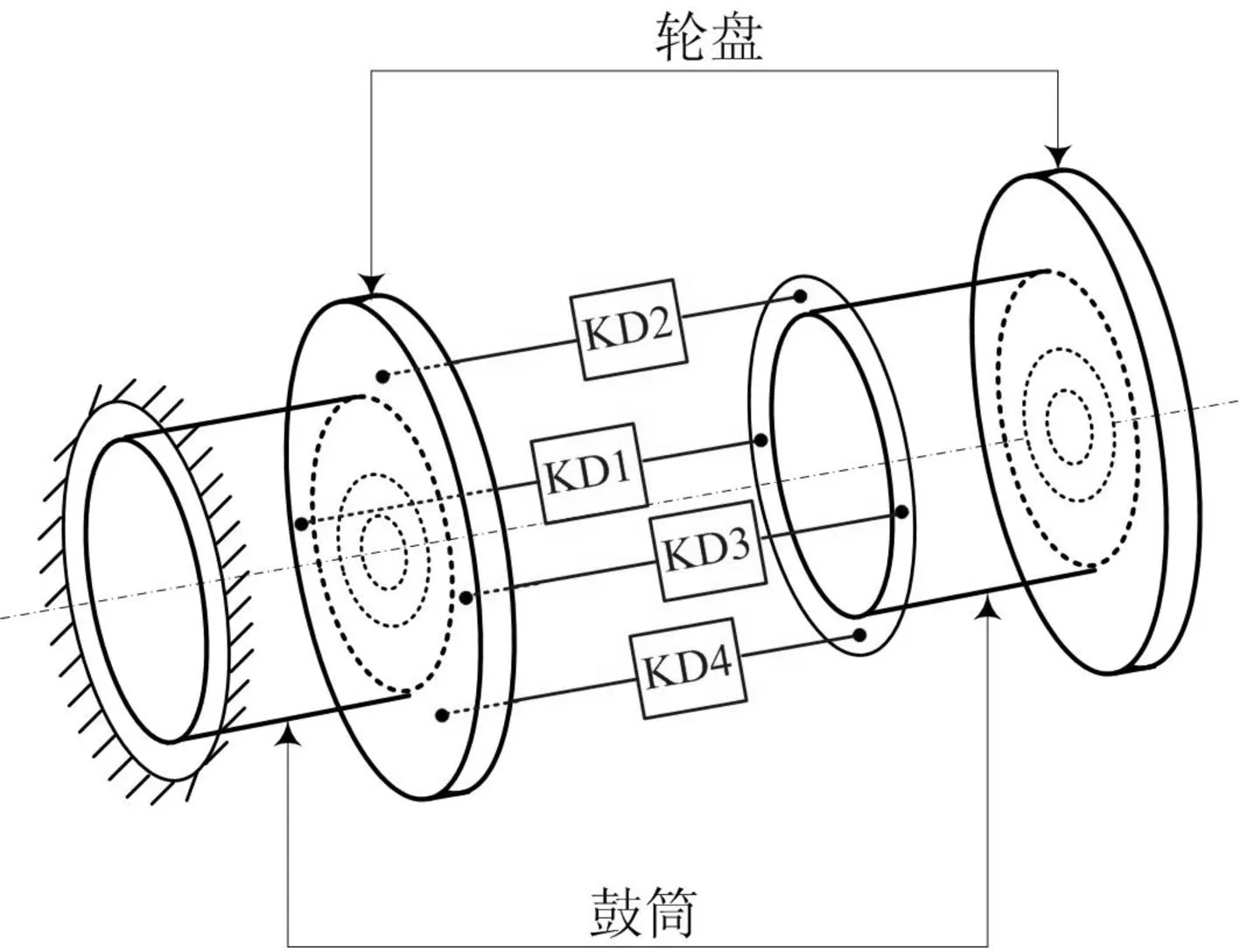
圖1　鼓筒-輪盤力學模型Fig.1 Mechanical model of the drum-disk

參數量值單位軸向剛度kz1,kz2,kz3,kz41.2×109N/m軸向阻尼dz1,dz2,dz3,dz41.5×105Ns/m周向剛度kθ1,kθ2,kθ3,kθ41.0×108N/m周向阻尼dθ1,dθ2,dθ3,dθ41.0×105Ns/m徑向剛度kr1,kr2,kr3,kr41.0×108N/m徑向阻尼dr1,dr2,dr3,dr41.0×105Ns/m

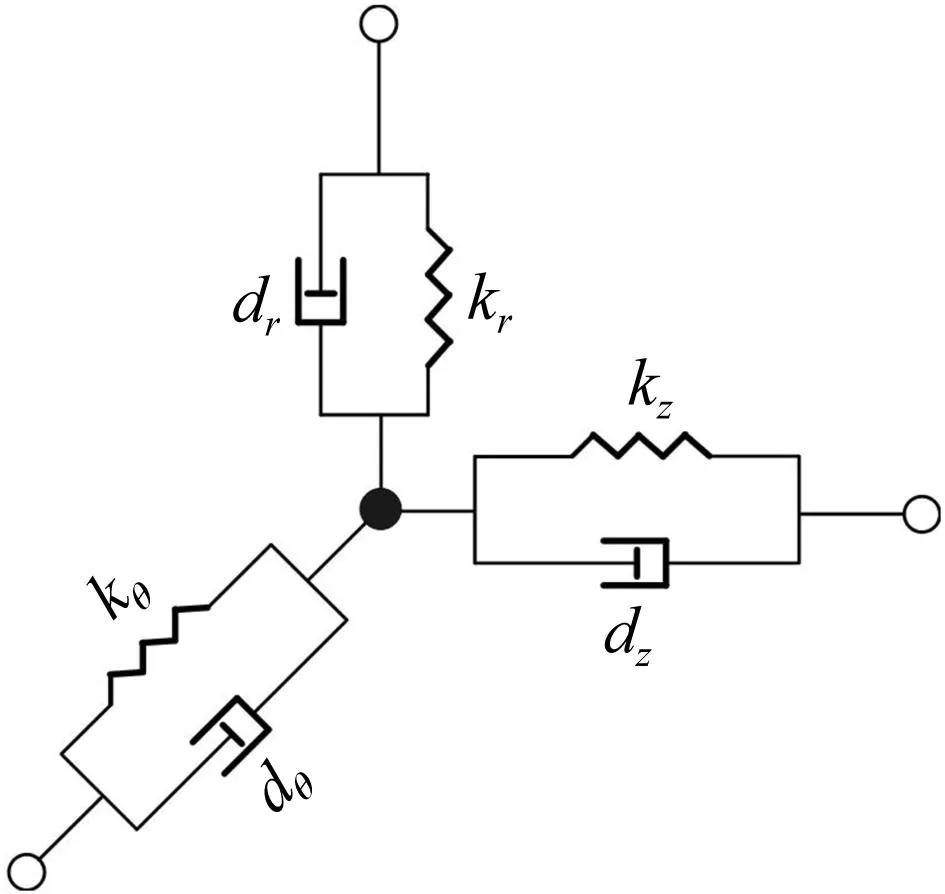
圖2　結合部連接單元Fig.2 Connecting element of the joint

2辨識原理

以結合部軸向連接剛度和阻尼的識別說明參數辨識的基本原理。不考慮結合部連接子結構時，鼓筒-輪盤的運動方程可表示為：

(1)

式中M，D，K，F分別表示被聯接結構的質量、阻尼、剛度矩陣以及作用于被聯接結構的力向量；Xa，Xb分別表示左端鼓筒-輪盤和右端鼓筒-輪盤位于連接界面的耦合運動坐標；XA，XB分別表示左端鼓筒-輪盤和右端鼓筒-輪盤的非耦合運動坐標。

由式(1)可得整體系統在不考慮結合部連接子結構時的動剛度Z：

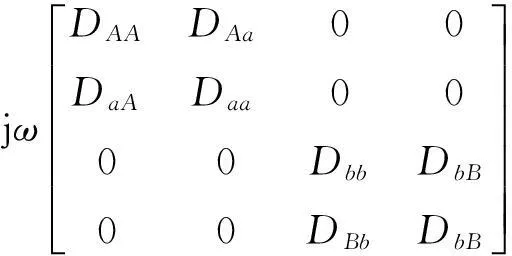
(2)

式中,Z,H分別表示不考慮結合部連接子結構時鼓筒-輪盤的動剛度矩陣和頻響函數矩陣；ω為激勵頻率。

假設所有彈簧與阻尼器彼此獨立，結合部連接子結構的運動方程可表示為：

(3)

式中,kzi、czi(i=1,2,3,4)分別表示連接結合部的軸向等效剛度和軸向等效阻尼。

由式(3)可得結合部連接子結構的動剛度ZJ：

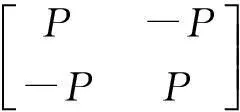
(4)

(5)

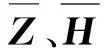
由方程(2)和(5)可得

(6)

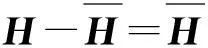
(7)

為了盡可能多地利用原點頻響函數信息，同時又盡量少地利用經過換算的頻響函數，選擇式(7)的子式(8)辨識鼓筒-輪盤結合部的連接剛度和阻尼參數。由于篇幅的限制，具體的參數辨識過程參見文獻[15]提出的基于實測頻響函數的基本識別算法。

(8)

3選點原則

為了準確高效地識別連接結合部的連接剛度和阻尼參數，頻響數據的選擇是一個至關重要的問題。現有研究多依靠經驗進行選擇，導致參數辨識的準確性差，效率低。為此本文提出選擇頻響數據的定性原則：所選取的局部信噪比最高的頻點所對應的模態對連接剛度的綜合靈敏度應該最高。

3.1振動模態計算

為了預測要選取的局部信噪比最高的頻點，首先將連接剛度代入圖1所示的力學模型，利用有限元法計算鼓筒-輪盤的振動頻率和模態振型。表2所示為鼓筒-輪盤前12階振動頻率的計算值，圖3所示為前12階模態振型的計算結果。

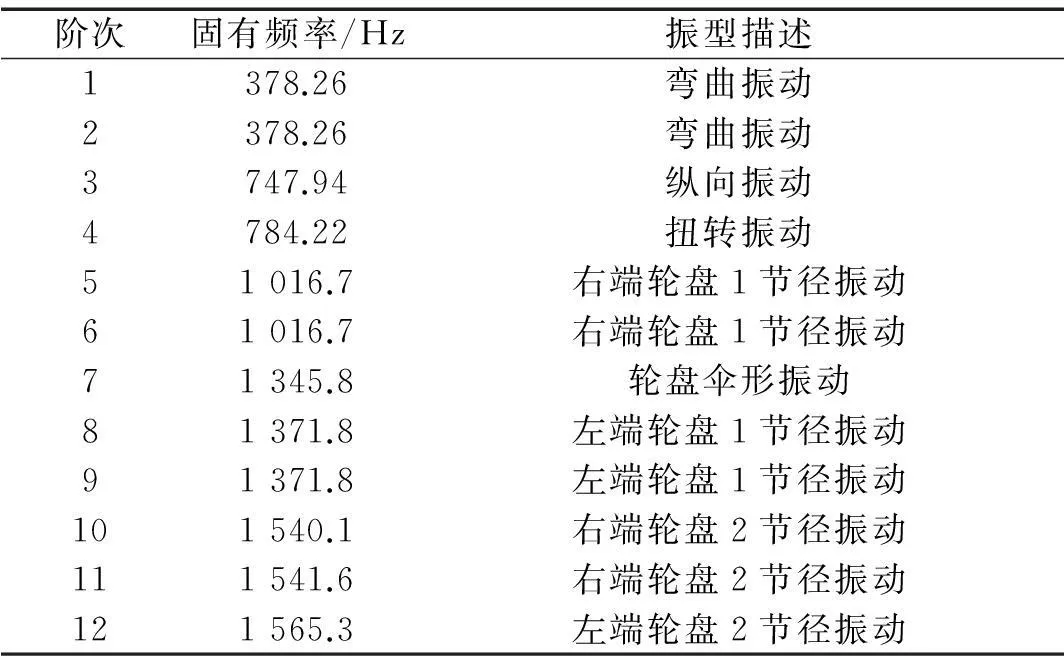
表2　鼓筒-輪盤振動頻率計算值

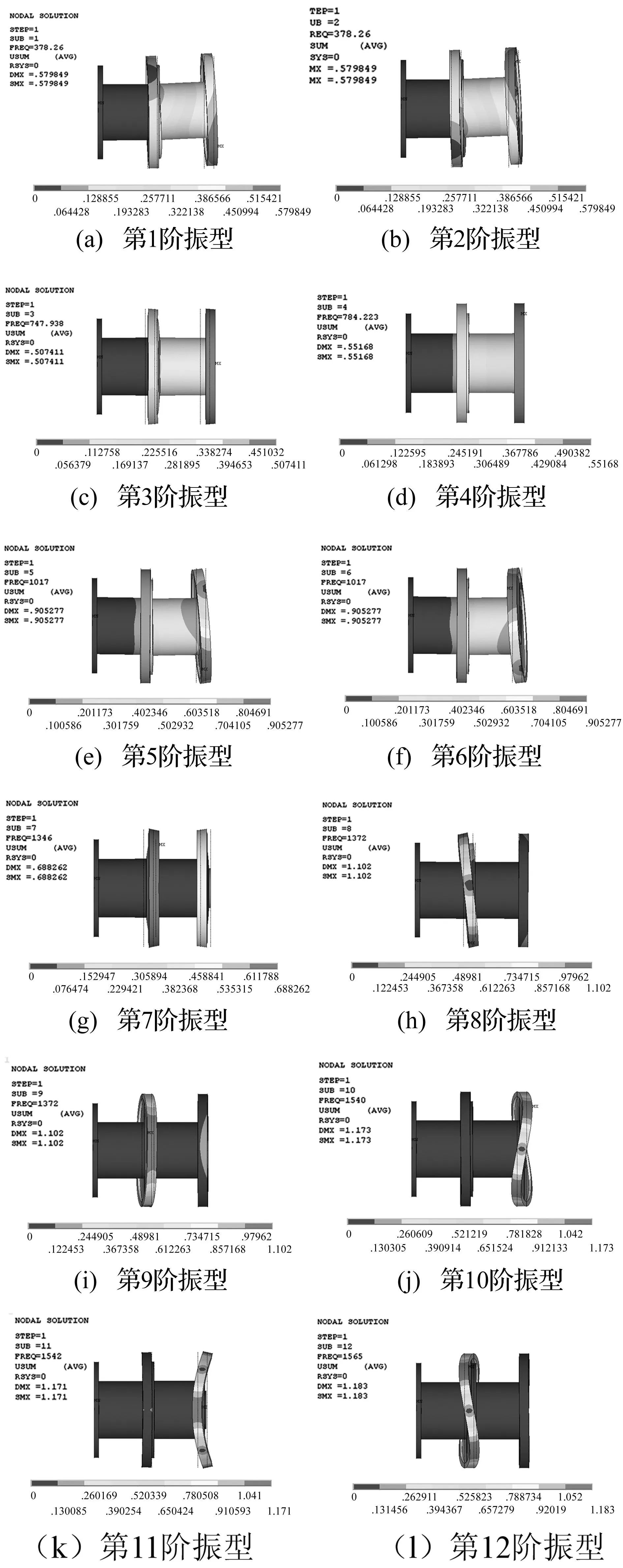
圖3　鼓筒-輪盤前12階模態振型Fig.3 The first twelve mode of the drum-disk

3.2量化標準

為了定量比較不同模態對結合部連接剛度的綜合靈敏度，必須建立具體的量化指標和標準。

(9)

式中,Sji綜合反映了鼓筒-輪盤固有頻率對結合部連接剛度的靈敏度，稱為綜合靈敏度。

綜合靈敏度越高，表示鼓筒-輪盤振動模態對結合部連接剛度越敏感，對應的頻響信息用于辨識結合部連接參數越有利。因此，應選擇綜合靈敏度最高的頻點所對應的頻響數據識別結合部連接參數。

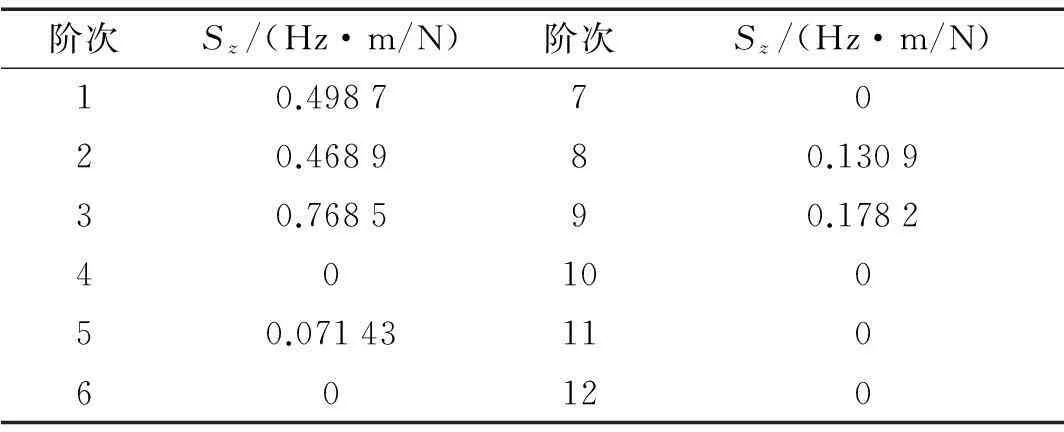
表3　固有頻率對軸向連接剛度kz1, kz2, kz3, kz4的綜合靈敏度

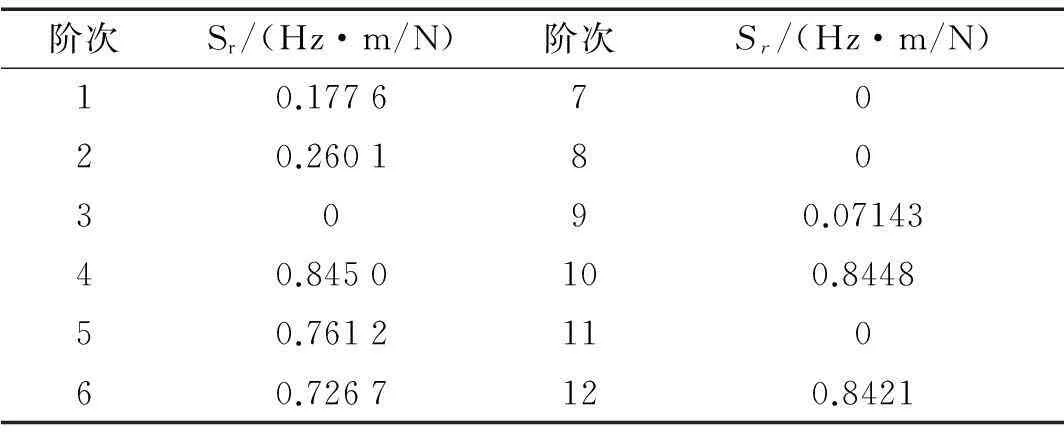
表5　固有頻率對徑向連接剛度kr1, kr2, kr3, kr4的綜合靈敏度

由表3～表5可以看出，鼓筒-輪盤第3階模態(縱向振動)對結合部軸向連接剛度的綜合靈敏度最高，第11階模態(右端輪盤2節徑振動)對結合部周向連接剛度的綜合靈敏度最高，第4階模態(扭轉振動)對結合部徑向連接剛度的綜合靈敏度最高，所以根據量化標準，應該分別選擇頻率為747.94 Hz、1541.6 Hz、784.22 Hz附近的頻響數據辨識結合部的軸向、周向、徑向連接參數。

4頻響函數計算

根據圖4～圖6所示的頻響函數曲線并結合3.2的分析可知，應分別選擇頻點750.5 Hz、1541 Hz、1 108 Hz所對應的頻響數據辨識鼓筒-輪盤結合部軸向、周向、徑向的連接參數。

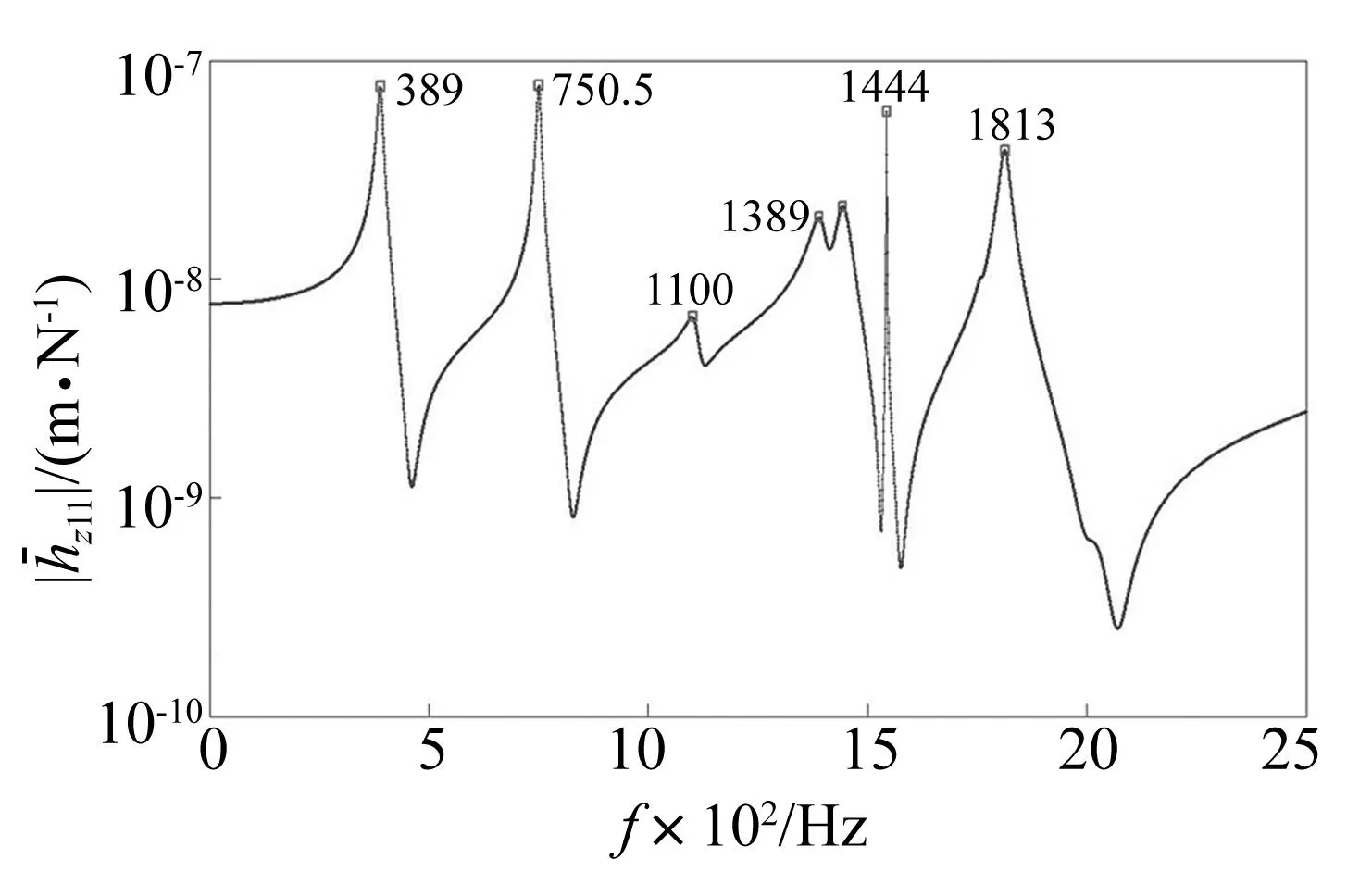
圖4　軸向位移頻響函數z11的幅頻特性曲線Fig.4 The amplitude-frequency curve of axial FRF z11

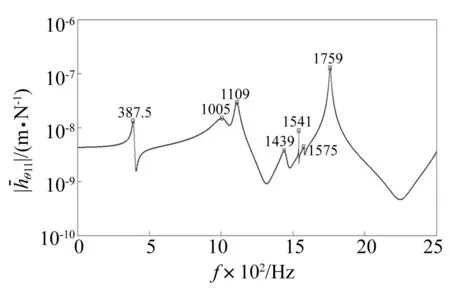
圖5　周向位移頻響函數θ11的幅頻特性曲線Fig.5 The amplitude-frequency curve of circumferential FRF θ11

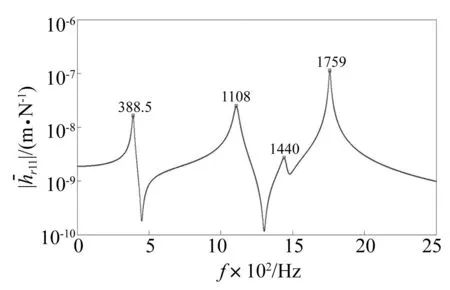
圖6　徑向位移頻響函數r11的幅頻特性曲線Fig.6 The amplitude-frequency curve of radial FRF r11

5辨識結果及驗證

表6～表8所示為依靠經驗選取高信噪比頻點辨識得到的鼓筒-輪盤結合部軸向、周向和徑向連接參數，表9～表11所示為根據本文提出的選點原則辨識得到的鼓筒-輪盤結合部軸向、周向及徑向參數。對比表8、表11可以明顯看出，依靠經驗選點辨識得到的結合部徑向連接參數均為負值，沒有物理意義，而根據本文提出的選點原則辨識得到的結合部連接參數均為正值，具有明確的物理意義。

表6　依靠經驗選點辨識得到的軸向連接剛度和阻尼

表7　依靠經驗選點辨識得到的周向連接剛度和阻尼

表8　依靠經驗選點辨識得到的徑向連接剛度和阻尼

表9　根據選點原則選點辨識得到的軸向連接剛度和阻尼

表10　根據選點原則選點辨識得到的周向連接剛度和阻尼

表11　根據選點原則選點辨識得到的徑向連接剛度和阻尼

為了對比依靠經驗選點與根據本文提出的選點原則選點辨識得到的結合部連接參數識別精度，進行相對誤差分析，如表12～表14所示。由相對誤差分析結果可以看出，依據本文提出的選點原則選點辨識得到的鼓筒-輪盤結合部連接參數具有較高的精度，充分說明本文提出的選點原則及量化指標是有效的，而依靠經驗選點辨識得到的連接參數精度較差，不能滿足工程精度要求。

表12　軸向連接參數識別結果相對誤差

表13　周向連接參數識別結果相對誤差

表14　徑向連接參數識別結果相對誤差

6結論

針對結合部采用彈簧和阻尼器連接的鼓筒-輪盤模型，開展了基于頻響函數的結合部連接參數識別研究，結論如下：

(1) 針對鼓筒-輪盤結合部連接參數的辨識，提出了頻響數據的選點原則，即所選取的局部信噪比最高的頻點所對應的模態對連接剛度的綜合靈敏度應該最高。

(2) 為了定量比較不同模態對連接剛度的綜合靈敏度，提出了衡量綜合靈敏度大小的量化指標和標準。

(3) 理論分析結果表明本文提出的頻響數據選點原則和量化標準是合理的。

(4) 本文所提出的頻響數據選點原則和量化標準為實際復雜結構結合部參數辨識提供了有意義的參考，具有一定的工程應用價值。

參 考 文 獻

[ 1 ] Ibrahim R A, Pettit C L. Uncertainties and dynamic problems of bolted joints and other fasteners [J]. Journal of Sound and Vibration, 2005, 279: 857-936.

[ 2 ] 蔡力鋼, 郝宇, 郭鐵能, 等. 螺栓結合面法向靜態剛度特性提取方法研究[J]. 振動與沖擊, 2014, 33(16): 18-23.

CAI Li-gang, HAO Yu, GUO Tie-neng, et al. Method ofextracting normal static stiffness of bolted joint interfaces [J]. Journal of Vibration and Shock, 2014,33(16):18-23.

[ 3 ] Wang Mian, Wang Dong, Zheng Gang-tie. Joint dynamic properties identification with partially measured frequency response function [J]. Mechanical Systems and Signal Processing, 2012, 27: 499-512.

[ 4 ] Yuan J X, Wu S M. Identification of the joint structural parameters of machine tool by DDS and FEM [J]. Journal of Engineering for Industry, 1985, 107(1): 64-69.

[ 5 ] Kim T R, Wu X M, Eman K F. Identification of the joint parameters for a taper joint [J]. American Society of Mechanical Engineers, Journal of Engineering for Industry, 1989, 111: 282-287.

[ 6 ] Yang K T, Park Y S. Joint structural parameter identification using a subset of frequency response function measurements [J]. Mechanical Systems and Signal Processing, 1993, 7(6): 509-530.

[ 7 ] Hwang H Y. Identification techniques of structure connection parameters using frequency response function [J]. Journal of Sound and Vibration, 1998, 212: 469-479.

[ 8 ] Yang T, Fan S H, Lin C S. Joint stiffness identification using FRF measurements [J]. Computers and Structures, 2003, 81: 2549-2556.

[ 9 ] Wang J H, Chuang S C. Reducing error in the identification of structural joint parameters using error function [J]. Journal of Sound and Vibration, 2004, 273: 295-316.

[10] 郭鐵能, 李玲, 蔡力鋼, 等. 基于頻響函數辨識機械結合部動態參數的研究[J]. 振動與沖擊, 2011, 30(5): 69-72.

GUO Tie-neng, LI Ling, CAI Li-gang, et al.Identifying mechanical joint dynamic parameters based on measured frequency response functions [J]. Journal of Vibration and Shock, 2011, 30(5): 69-72.

[11] 蔡力鋼, 李玲, 郭鐵能, 等. 基于不完備頻響函數辨識結合部參數的研究[J]. 振動工程學報,2011,24(4):345-350.

CAI Li-gang, LI Ling, GUO Tie-neng, et al. Identifying mechanical joint dynamic parameters based on incomplete frequency response functions [J]. Journal of Vibration Engineering, 2011, 30(5): 69-72.

[12] 李玲, 蔡力鋼, 郭鐵能, 等. 機械結合部動態剛度辨識與實驗研究[J]. 振動工程學報, 2012, 25(5):488-496.

LI Ling, CAI Li-gang, GUO Tie-neng, et al.Identification and experimental research on dynamic stiffness of mechanical joints [J]. Journal of Vibration Engineering, 2012, 25(5):488-496.

[13] Nassar S A, Abboud A. An improved stiffness model for bolted joints [J]. Journal of Mechanical Design, 2009, 131(121001): 1-11.

[14] Eriten M, Lee C H, Polycarpou A A. Measurements of tangential stiffness and damping of mechanical joints: Direct versus indirect contact resonance methods [J]. Tribology International, 2012, 50: 35-44.

[15] 陳新. 機械結構動態設計理論方法及應用[M]. 北京:機械工業出版社,1997.

A principle of selecting points for identifying joint part parameters of a drum-disk structure based on frequency-response functions

WANGHong-yu1,QINZhao-ye1,CHUFu-lei1,LIUYan-qi2(1. State Key Laboratory of Tribology, Tsinghua University, Beijing 100084, China；2. Beijing Key Laboratory of Environment Noise and Vibration, Beijing Municipal Institute of Labour Protection, Beijing 100054, China)

Abstract:Methods based on frequency-response functions (FRFs) are widely used to identify joint part parameters. A key problem in FRFs-based methods is how to choose FRFs data for joint part parametric identification. Here, a principle for FRFs data selection and a quantitative criterion corresponding to the principle were proposed based on a drum-disk model. The drum and the disk were combined with springs and dampers at the connected joint. The proposed principle was that the comprehensive sensitivity of the mode which corresponds to the selected frequency point with the highest local signal-to-noise ratio (SNR) to the joint stiffness should be the maximum. In order to compare the comprehensive sensitivities of different modes, a quantitative index was subsequently established. The study showed that the proposed principle and the quantitative criterion are effective and valuable in engineering application.

Key words:connected joints; frequency-response function; parametric identification; principle of selecting points; quantitative index

中圖分類號:TH113；TB123

文獻標志碼：A

DOI:10.13465/j.cnki.jvs.2016.05.012

通信作者褚福磊 男，博士, 教授, 博士生導師, 1959年生

收稿日期：2015-01-23修改稿收到日期：2015-03-19

基金項目：國家自然科學基金(11472148;11102093)；北京市自然科學基金(3143024)

第一作者 王洪玉 男，博士, 1982年生