導體電阻率的統計動力學機制

張太榮，劉松紅(六盤水師范學院物理與電子科學系，貴州六盤水553004)

?

導體電阻率的統計動力學機制

張太榮，劉松紅
(六盤水師范學院物理與電子科學系，貴州六盤水553004)

摘要：從經典統計出發，基于電子的隨機行走模型，使用蒙特卡洛方法進行數字模擬，給出了高斯分布、lévy分布等條件下導體的電阻率特征及機制。

關鍵詞：統計動力學；高斯分布；lévy分布；溫度；電阻率

On the Statistical Dynamics Mechanism of the Conductor Resistivity

ZHANG Tai-rong，LIU Song-hong
(Physics and Electronic Sciences Department, Liupanshui Normal University, Liupanshui 553004, China)

由于導體的電阻是產生焦耳熱的根本原因，是電磁能量傳輸損耗的主要因素，因此良導體的尋找（諸如高溫超導材料）是目前科學技術界的重要研究方向。1911年昂內斯（Onnes）發現了超導現象；1950年倫敦（London）和金茲堡-郎道（Ginzbao-Langdau）基于經典電動力學分別對超導現象給出了唯象解釋。1957年巴丁（J.Bardeen）、庫伯（L.N.Cooper）、施里弗（J.R.Schrieffer）用電子-聲子機制建立了BCS理論，就低溫超導機制給出了電子庫伯對的解釋，成功地解釋了低溫超導現象。1986年穆勒（Muller）和柏諾茲（Bednorz）發現陶瓷氧化物LaBaCuO的超導轉變溫度可達到35K，此高溫超導現象至今仍然沒有較為公認的理論解釋[1]。導體的電阻率是導體的一個基本特性。在經典范疇，導體的電阻率本質上是由導體的晶格結構及電子熱運動對輸運電子的作用所致，即處于晶格中的電子受外場作用遷移時，其阻尼主要來源于自由電子的熱運動、晶格的散射、晶格中周期場的作用。對于導體電阻率的經典統計動力學機制，并沒有文獻報道。利用統計動力學方法研究經典模型下晶格中的電子輸運，給出導體電阻率的經典統計動力學機制，有助于物理教學及高溫超導機制的研究。

1導體中經典電子的輸運

1.1弱周期勢近似下的電子輸運

弱周期近似，是指粒子電子在外場作用下進行輸運時，忽略晶格的散射和周期場的作用，只考慮自由電子的熱運動，此時電子之間的相互作用是導致電阻的主要因素。在均勻外場的作用下，電子的動力學運動服從郎之萬（Langevin）方程[2]。

1.2緊束縛近似下的經典電子輸運模型

緊束縛近似是粒子電子在外電場作用下進行輸運時，除受到自由電子的熱運動影響外，還受到晶格的周期場的散射作用。此時電子的動力學運動滿足廣義郎之萬方程。

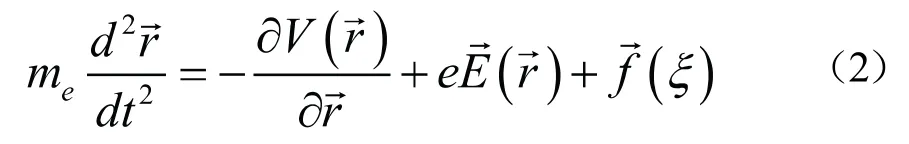
2數值模擬結果

2.1弱周期勢的動力學特征

考慮短弛豫近似，電子每次所受熱運動碰撞的時間間隔近似相等。在空間各向同性的情況下，電子在空間的分布均勻。最簡單情形，考慮一維晶格中的運動，采用無量綱標度，并且外電場為均勻場，則電子運動的郎之萬方程為：

考慮輸運時間為：

第i次碰撞導致電子的空間遷移為：

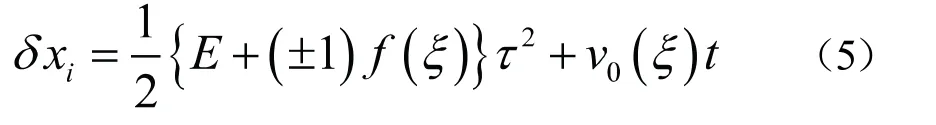
于是，一維晶格的電阻為：

采用乘分布舍選法進行抽樣[3]，

作變量代換：

取中間函數H(x)：

則H(x)的極值為M。

則可得到滿足麥克斯韋速率分布的隨機速率的平方值：

圖1弱周期近似下高斯分布時電流隨溫度的變化（恒定電壓條件）

（2）在隨機力為均勻分布時（白噪聲），I-T關系如圖2所示。使用Matlab7.0軟件。從圖2的I-T關系看出，在絕對零度時出現了電子的凝聚（絕緣態），此時電流為零。溫度較低時，電阻隨溫度迅速降低（恒定電壓下的電流迅速增大），說明電子的熱運動決定了介質的導電特性。有明顯的溫度拐點，拐點后的電阻幾乎不隨溫度變化，此時表現為電子數密度決定了介質的導電特性。

圖2弱周期近似時均勻分布條件下電流與溫度的變化關系

（3）在隨機力滿足lévy分布[4]時（冪律白噪聲），

采用直接抽樣時，為防止抽樣時的發散，采取低端截斷。得到電場恒定時I-T關系如圖3所示。使用Matlab7.0軟件模擬。此處取指數指標為=1.5，采用直接抽樣方法，得到噪聲的隨機樣本為：

圖3弱周期近似下穩恒場中lévy分布對應的電流-溫度關系

從圖3的T-I關系可看出，沒有絕緣狀態，沒有溫度拐點，電阻隨溫度呈線性變化。超擴散的量子特征在此沒有體現出預期的超導現象。

2.2在緊束縛近似下的動力學特征

考慮晶格對輸運電子的作用近似為對稱鋸齒勢：

圖4晶格對輸運電子的對稱鋸齒勢

（1）麥克斯韋分布條件下的動力學特征

采用隨機行走模型，在無量綱標度下，勢井深度為擾動的100倍時，高斯分布（白噪聲）情況下，確定導體的電流在恒定電壓下隨溫度的變化的數值模擬結果如圖5所示（采用Matlab7.0模擬）。從圖56可以看出，出現了介質絕緣-導電的溫度轉換點。介質轉換為導體后，電阻隨溫度線性下降。

圖5緊束縛條件下高斯分布時恒定電場中電流隨溫度的變化

（2）lévy分布下的動力學特征

采用勢井深度為隨機擾動的1000倍，在無量綱標度下，于常溫范圍，得到lévy分布時的電流隨溫度的變化如圖6所示（采用Matlab7.0模擬），出現了恒溫電阻的現象，是高溫陶瓷材料的基本特征。

圖6緊束縛近似下lévy分布時電流溫度關系

3結論

從蒙特卡洛的數值模擬情況來看，經典帶電粒子的熱運動對導體電阻的貢獻，主要表現為電阻的負溫度特性（導體的電阻隨溫度增加而減少）,這個規律與通常態的純凈金屬導體的溫度特性相一致。同時在低溫下，并沒有出現零電阻特征（電場恒定時，沒有無窮大電阻的出現）。由此更進一步證明了用經典的電子熱運動模型不能對物質的超導現象進行解釋。

參考文獻：

[1]郭碩鴻.電動力學(第三版)[M].北京:高等教育出版社,2008. 92-102.

[2]H Risken.The Forkker-Planck Equation[M].北京:世界圖書出版公司,1984.32-36.

[3]張太榮.統計動力學及其應[M].北京:冶金工業出版社,2007. 159-164.

[4]R Metzler,J Klafter.The random walk’s guide to anomalous diffusion:a fractional dynamics approach[DB/OL].(2015-08-14) http://www.docin.com/p-632676442.html

（責任編輯：朱彬）

Key words：By means of classicalstatistics and on the basis of random walk model of electronics,the author of this paper uses Monte Carlo method to do digital simulation to discuss the resistivity characteristics and mechanism of conductor under the Gauss distribution, lévy distribution, etc. classical statistics dynamics; Gauss distribution; lévy distribution; temperature; resistivity

作者簡介：張太榮，男，貴州畢節人，六盤水師范學院物理與電子科學系教授，主要從事統計動力學研究。

收稿日期：2015-09-14

中圖分類號：O411

文獻標識碼：A

文章編號：1009-3583（2016）-0095-04