混合不確定度量化方法及其在計算流體動力學迎風格式中的應用*

梁 霄,王瑞利

(1.北京應用物理與計算數學研究所,北京 100094;2.山東科技大學數學學院,山東 青島 266590)

混合不確定度量化方法及其在計算流體動力學迎風格式中的應用*

梁 霄1,2,王瑞利1

(1.北京應用物理與計算數學研究所,北京 100094;2.山東科技大學數學學院,山東 青島 266590)

針對流體力學數值求解間斷問題時，初始狀態含有偶然和認知混合型的不確定性，將認知不確定度作為外層，偶然不確定度作為內層，分別使用非嵌入多項式混沌方法(non-intrusive polynomial chaos,NIPC)和概率盒(P-box)理論處理偶然不確定度和認知不確定度，發展了流體力學數值求解過程中，初始狀態含有混合不確定度傳播量化的一種方法。以迎風格式和黎曼解法器求解Sod問題為例，評估了左狀態密度(偶然不確定度)和理想氣體多方指數(認知不確定度)對模型輸出結果的影響，有效驗證了該方法的可行性。

爆炸力學;建模與模擬;非嵌入多項式混沌法;混合不確定度量化;概率盒

在重大復雜工程領域,眾多工程事故已經引發社會各界的關注。人們總是抱著一個良好的愿望,希望能逼真建模,研制高可信度的數值模擬軟件,精確模擬各類事故的發生過程，科學分析其產生的機理。因此,數值模擬軟件必須能真實反映實際系統的外部表征、內在特性及其動作行為等現象,其數值模擬結果才能使人置信。但由于物理過程的復雜性及人們的認知缺陷,物理建模與數值模擬始終存在誤差和不確定性。為此,要利用數值模擬結果分析機理和模擬過程,必須量化數值模擬結果的不確定性,評估建模與模擬的可信度。但長期以來,物理建模與數值模擬軟件的研制者重點關注的是軟件自身的研制和對實際問題的順利模擬,即算下去的問題,對軟件自身的正確性、模擬結果的不確定性和建模與模擬的可信度,即算多準的問題,一直沒有給予足夠的重視。尤其是對于理論、實驗無法解釋或難于解決的科學問題,或做實驗耗資巨大的工程設計,很想利用數值模擬真實、全過程,全系統、反復精密地進行模擬的研究者持一種矛盾的心態：既想利用數值模擬這條快捷經濟的重要研究途徑,又對程序的正確性和數值模擬提供的結果心存疑慮。為了給復雜裝置設計提供高效可靠的數值模擬工具,必須展開計算模型正確性和可信度的評估研究。

流體力學方程及求解方法是眾多復雜工程多物理過程建模與模擬(modeling & simulation，M&S)中的最基本模型,此計算模型的驗證與確認(verification and validation,V&V)受到高度重視[1-7]。W.L.Oberkampf等[8]綜述了機械工程領域中科學計算V&V的發展,系統論述了科學計算中V&V的基本概念、原理及步驟和發展過程。王瑞利等[5]綜述了V&V的相關概念、 術語、規范、可信度評估方法和應用等的研究進展,就M&S的V&V的幾個關鍵問題進行了概括,構建了復雜工程M&S的V&V的知識指南。確認是建立在定量準確評價的概念上,是評價模型描述實際物理過程/實驗(試驗)的準確程度、模型形式與參數的適應范圍,確認刻畫實際問題/實驗(試驗)區域的形狀,預測可信度評估等重要活動。對于流體力學確認的核心是隨機輸入參數對模擬輸出響應量不確定傳播進行量化的方法。

不確定度量化(uncertainty quantification,UQ)方法是利用各種數學和統計學方法,對隨機因素或認知缺陷盡可能給出分布或區間描述,建立建模和模擬中隨機或認知不確定性因素和建模與模擬描述系統響應量之間的關系,進而量化影響系統性能的不確定性,給出系統響應量性能分析的不確定度度量的方法。對于不確定度量化有多種方法,其中敏感度分析方法、抽樣方法、代理模型方法、隨機微分方程方法和參數率定與優化方法已在復雜工程中得到很好的應用。

在上述幾種方法中,隨機微分方程是20世紀中葉發展起來的一種不確定度量化方法。廣義的隨機微分方程包括隨機過程驅動的微分系統和系數為隨機量的微分方程,狹義上的隨機微分方程往往專指前者。對于隨機過程驅動的微分系統,方程的解往往是一個隨機過程函數。雖然求解常微分方程的方法不適用于求解隨機微分方程,然而,有些復雜過程可以直接使隨機過程建模、模型的不確定性,直接表現在模型本身上而不是輸入參數的不確定性,隨機微分方程是研究不確定度量化的很好途徑。另一方面,系數為隨機量的微分方程可以直接處理為隨機參數的微分方程,常見的分析方法是隨機譜方法。

隨機譜方法是使用譜逼近隨機微分方程或參量,然后將其分解為獨立的確定性分量和隨機分量來量化不確定性。其數學思想是數學模型中的每一個參量利用正交多項式如(如Hermite多項式)展開成無窮級數項,在實際應用中取有限項。無窮級數第1項表示參量的期望,第2項表示高斯隨機波動,第3項及高階項表示非高斯隨機波動。隨機譜方法已在建模和模擬不確定度量化中得到了廣泛應用。常見的2種方法:KL展開(Karhunen-Loeve expansion)和多項式混沌方法(polynomial chaos,PC)。本文中，將著重介紹PC在Riemann問題不確定度量化中的應用。

1 流體力學方程組與迎風格式

一維拉氏流體力學方程組[9]:

(1)

式中：ρ、u、E、e和p分別為流體密度、流體速度、總能、比內能和流體壓強,v為比容,γ為理想氣體多方指數。一維拉氏流體力學方程組迎風型格式見文獻[9]

2 多項式混沌法

多項式混沌法其數學思想是數學模型中的每一個參量利用正交多項式(如Hermite多項式)展開成無窮級數項。設系統的解具有如下形式：

(2)

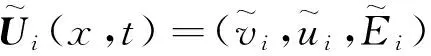
(3)

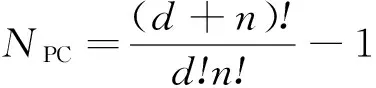
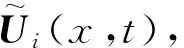
IPC是將數學模型中的每個參量進行正交多項式展開,然后利用Galerkin映射,得到相應的隨機控制方程,但是每一次展開都需要重新書寫控制方程。因此，IPC無法利用已有程序,需要對已有的數值求解程序進行大量修改或者重新研制計算程序。

NIPC是把已有的數值求解程序作為一個黑匣子,在隨機空間里通過一定的抽樣方法,獲得若干個樣本點,將樣本點輸入到確定性程序求解,然后對確定性輸出結果進行統計分析,以獲得相關數值求解結果的統計特征,來評估輸入參數或計算條件的不確定性在計算過程中傳播的影響。NIPC采用已有的數值模擬程序,不需要對控制方程進行修改,不需要重新編寫程序。NIPC不確定度評估的計算流程見文獻[7]。

3 P-box的構造方法

若問題中同時存在偶然不確定和認知不確定,需要將其結合起來考慮,此時可采用概率盒方法進行描述，即將各參數分為內外2層循環：外層循環考慮認知不確定參數,使用拉丁超立方取樣(Latin hypercube sampling,LHS)方法抽樣；內層循環考慮偶然不確定參數,取值由隨機抽樣給出。

P-box計算步驟:

(1)外層循環考慮認知不確定參數,從其區間中,采用LHS方法得到N個樣本；內層循環考慮偶然不確定參數,利用Monte Carlo(MC)抽樣得到M個樣本,作為左端密度初值;

(2)固定一個外層認知不確定變量γ,計算出相應的M個結果;

(3)尋找相應物理量的最大、最小值,然后分成100份,計算每一份對應的樣本容量,繪出相應的累積分布曲線;

(4)對剩余的N-1個認知不確定數施行同樣運算,劃出N條累積分布曲線;

(5)選取最內層和最外層的那一條作為概率邊界，構成一個P-box;

(6)讀出概率盒的意義。

4 混合不確定量化方法在Sod問題中的應用

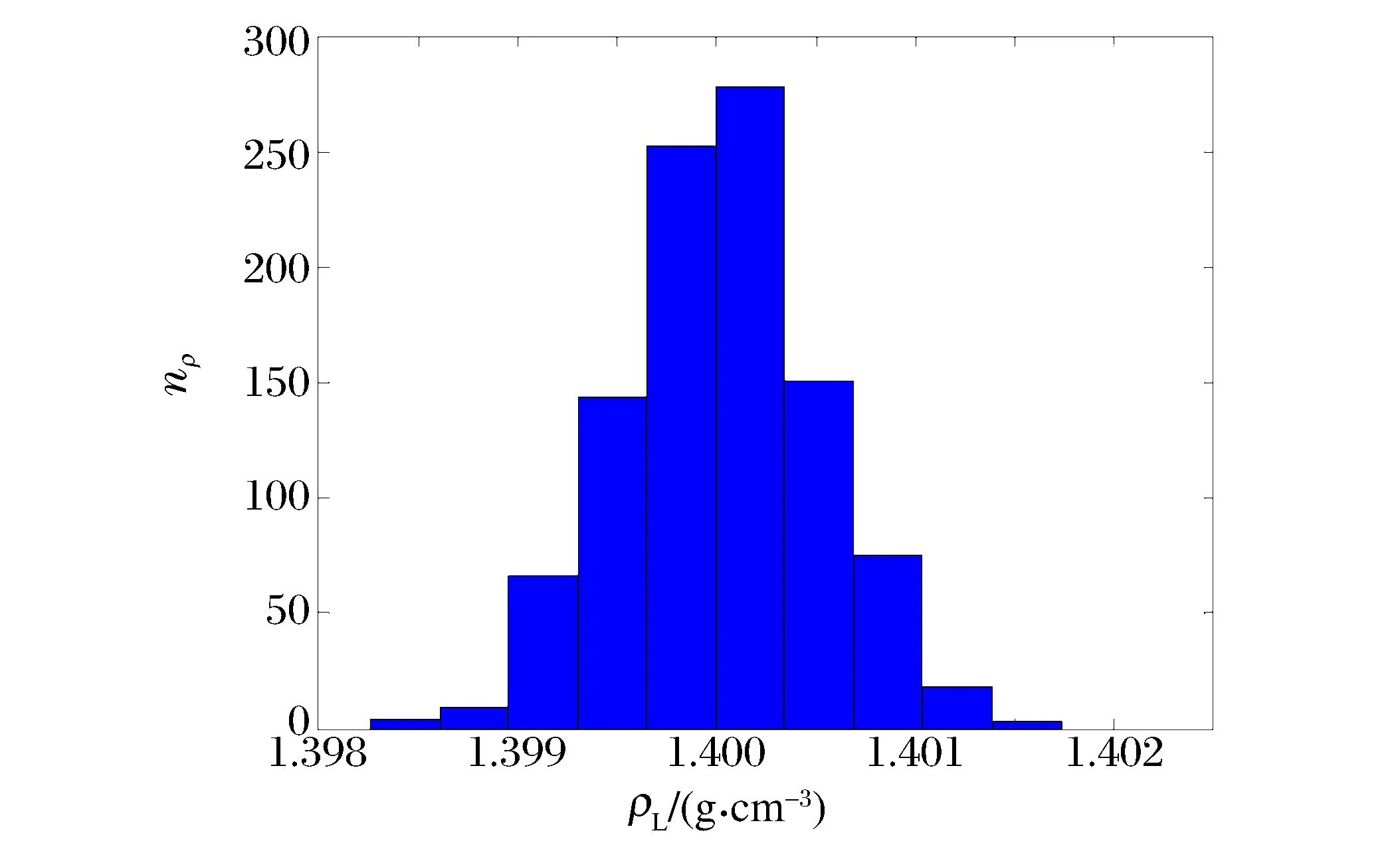
圖1 炸藥密度分布直方圖Fig.1 Histogram showing distribution of explosive density

Sod激波管問題是初始間斷的分解問題,在一個無限長管道中,在x=0處的左端是高壓氣體,右邊是低壓氣體,在初始時刻處于靜止狀態,兩者之間用薄膜隔離。t=0時刻薄膜破裂,形成向左稀疏波和向右激波。Sod問題計算區域為[-1,1],初值為:

x≤0時，ρL～N(1.0,2.5×10-7),uL=0.0,pL=1.0,γL∈[1.4,3.1];

x>0時,ρR=0.125,uR=0.0,pR=0.1,γR=1.4。

采用理想氣體狀態方程:

p=(γ-1)ρe

此問題的特點是左右2種狀態的γ不一樣,是一個多介質激波管問題,有解析解。但其中左右密度量含有不確定因素,對其量化才能實施計算模型的確認。對于左端炸藥密度,由于加工過程中炸藥顆粒凝結的不均勻性,導致密度存在隨機性。

假設其服從正態分布,期望為μ=1.4 g/cm3,標準差σ=0.5 mg/cm3,即炸藥密度服從正態分布：

N(μ,σ2)=N(1.4,1.5×10-7)

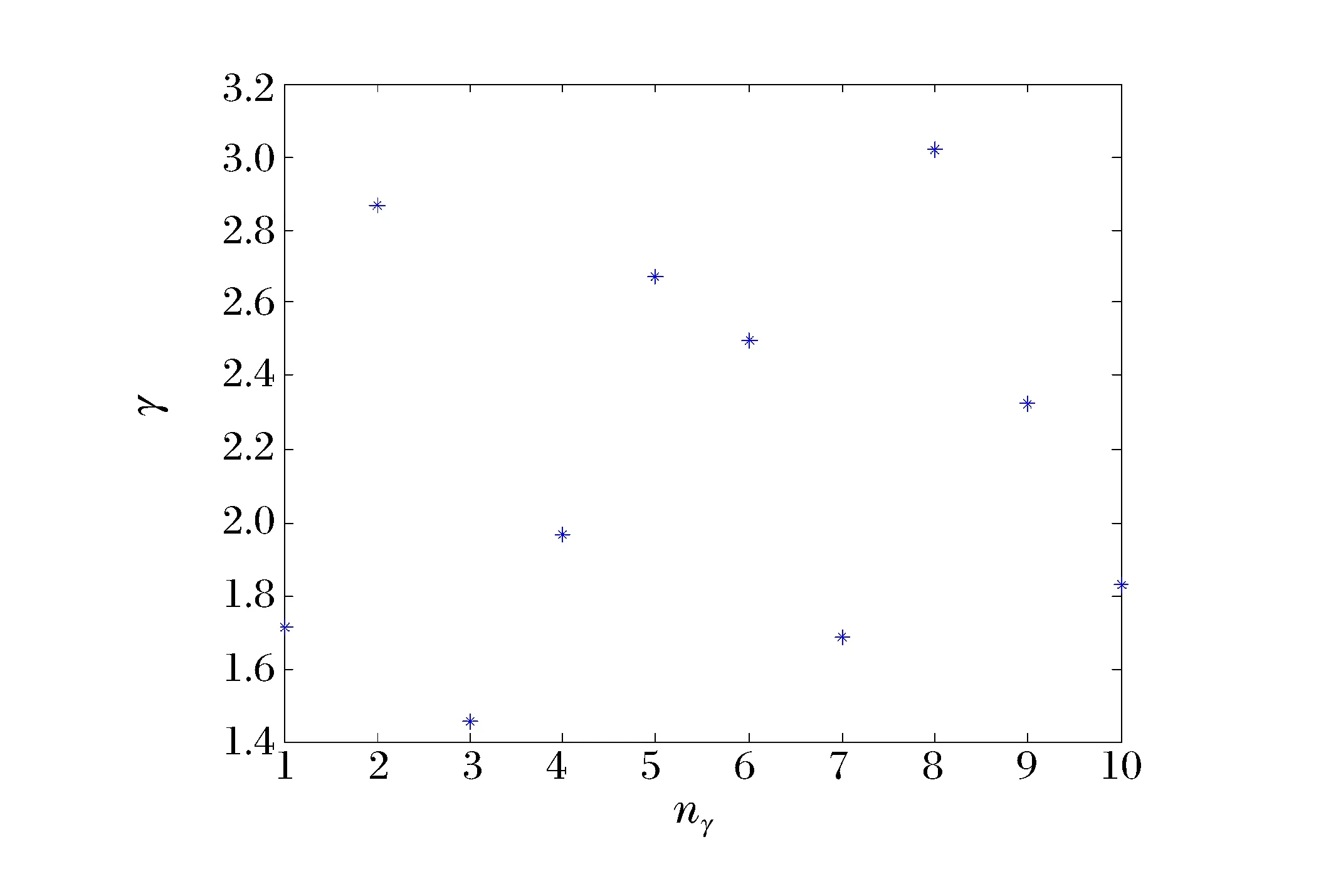
圖2 多方指數分布散點Fig.2 Scatter of polytrophic exponent

對炸藥密度采用MC方法,取樣1 000次,分布直方圖如圖1所示。

對于多方指數γ，不知道它的任何信息,只知道它位于[1.4，3.1],在實際設計或計算中采用哪個數值由設計者決定,這種選取的過程與認識水平有關,屬于認知不確定度。利用LHS采樣10次,如圖2所示。

當固定γ時,會得到1 000組狀態確定性Sod問題的樣本點,將其代入迎風格式的流體力學程序和精確解法器,得到1 000組響應量的樣本狀態,γ=2.29時,計算到t=0.22時,密度、壓力、速度、能量的狀態構成的馬尾圖,如圖3所示。從圖3可以看出,在某些地方解的分散度很明顯。當γ變化時,會得到10張類似的馬尾圖。

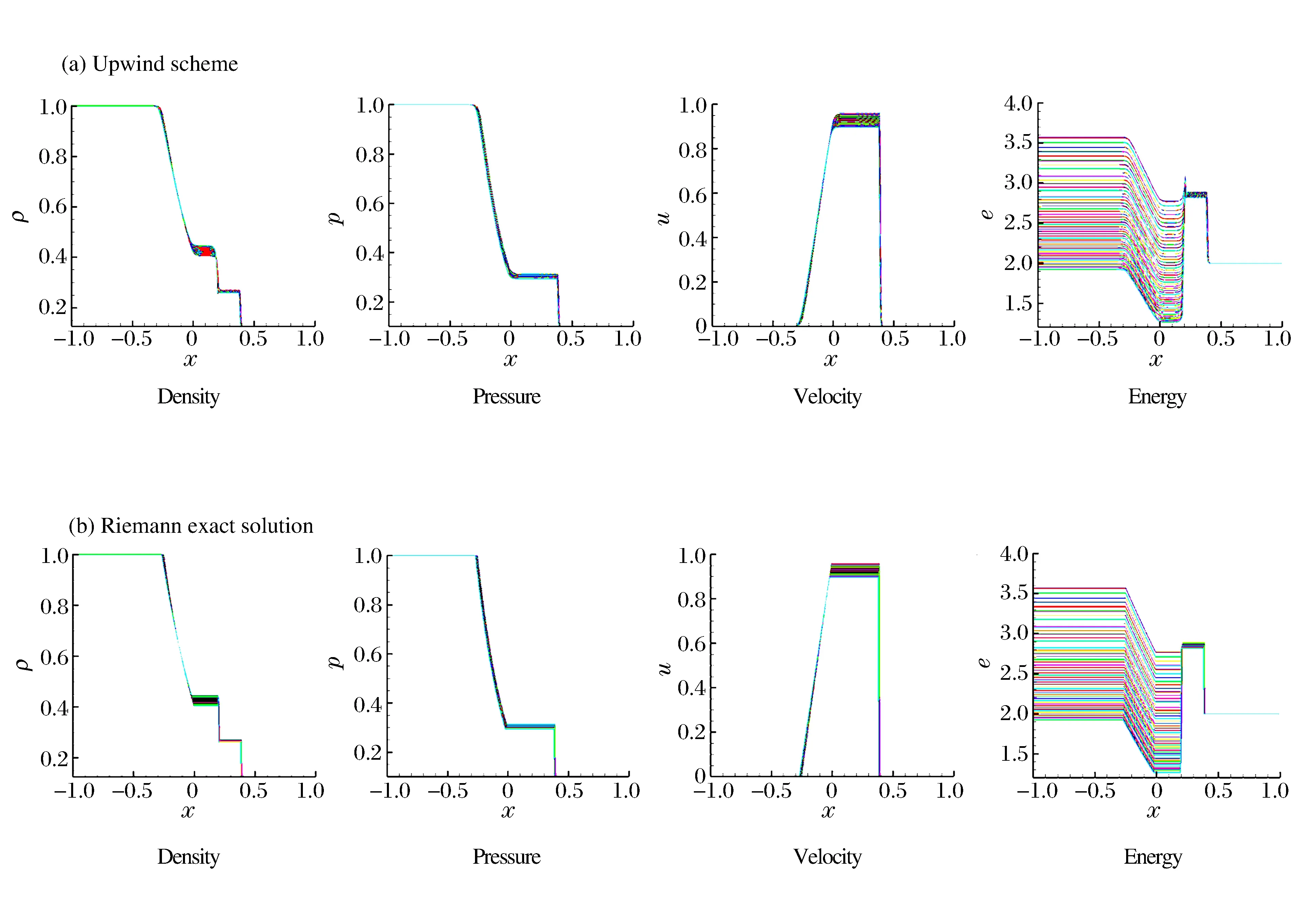
圖3 Sod問題1000組計算結果Fig.3 1000 sets of computational results for the Sod problem

4.1 可信范圍

對于上述計算結果,信息量巨大,現在提取有用的信息。首先,將10張馬尾圖合并,得到10×1 000=10 000組響應量樣本狀態,采用NIPC方法開展不確定度量化。

圖4給出了計算得到的密度、壓力、速度、能量的期望和方差,從圖可以看出有些地方方差很大,精確求解黎曼解法器的方差比迎風格式的高。

圖5給出了迎風格式可信范圍和精確黎曼解法器可信范圍,從圖可以看出有80%的地方完全重疊,其他局部重疊或者不重疊,說明采用迎風格式求解Sod問題是可信的。

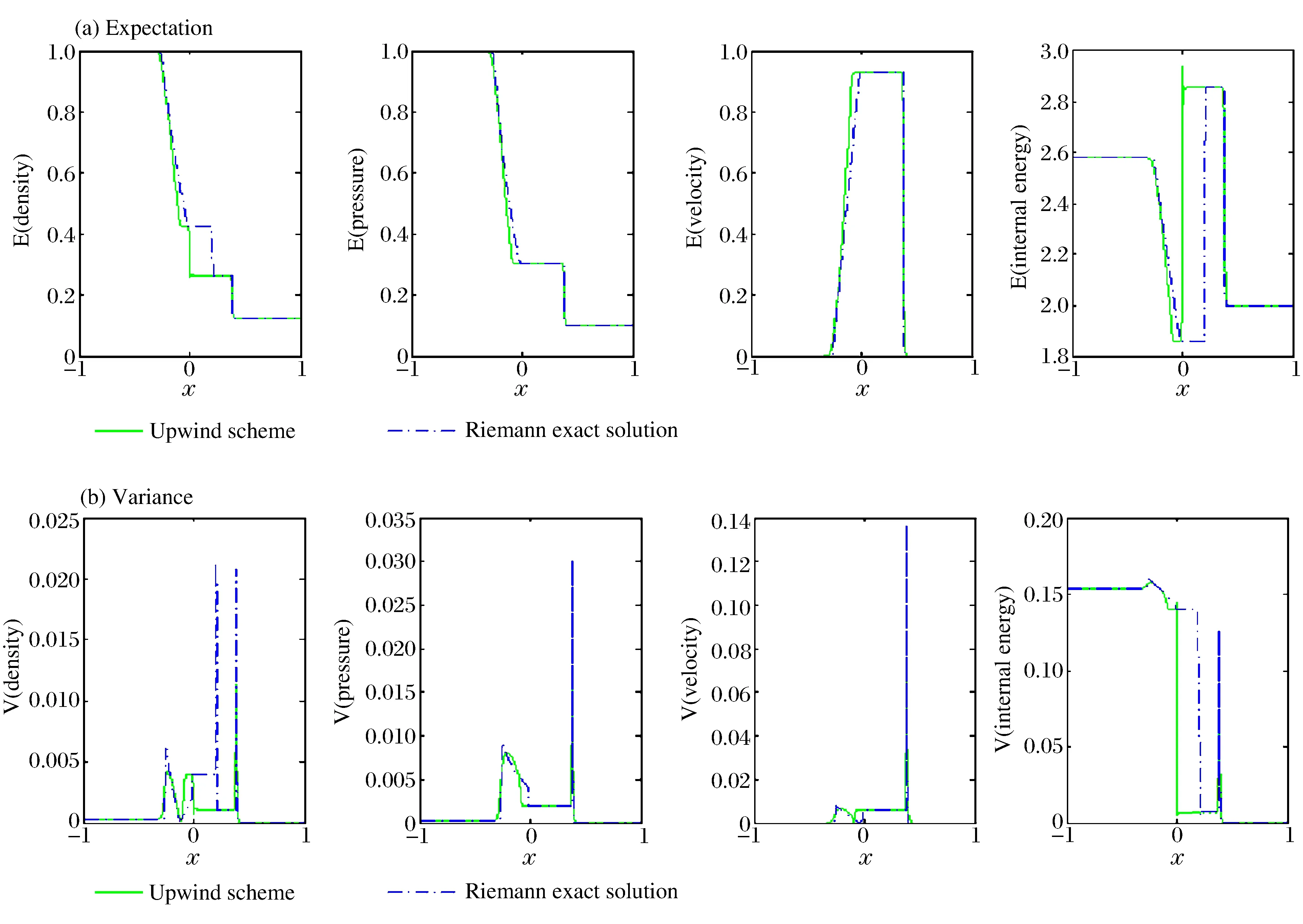
圖4 t=0.22時Sod問題的期望和方差Fig.4 Expectation and variance for the Sod problem at t=0.22

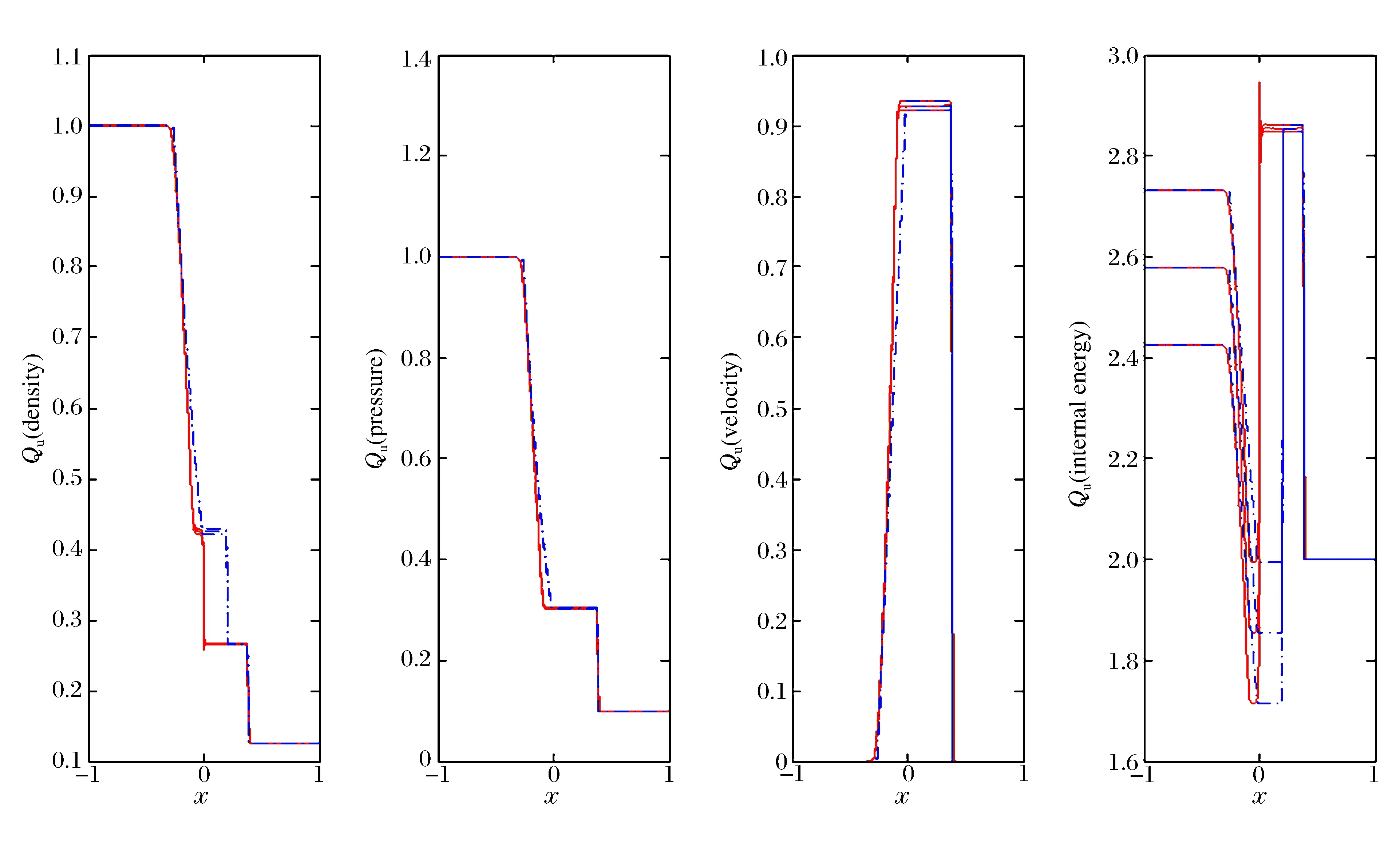
圖5 2種方法計算Sod可信區間的比較Fig.5 Comparison of confidential intervals from two computational methods in solving the Sod problem

4.2 Sod問題的P-box

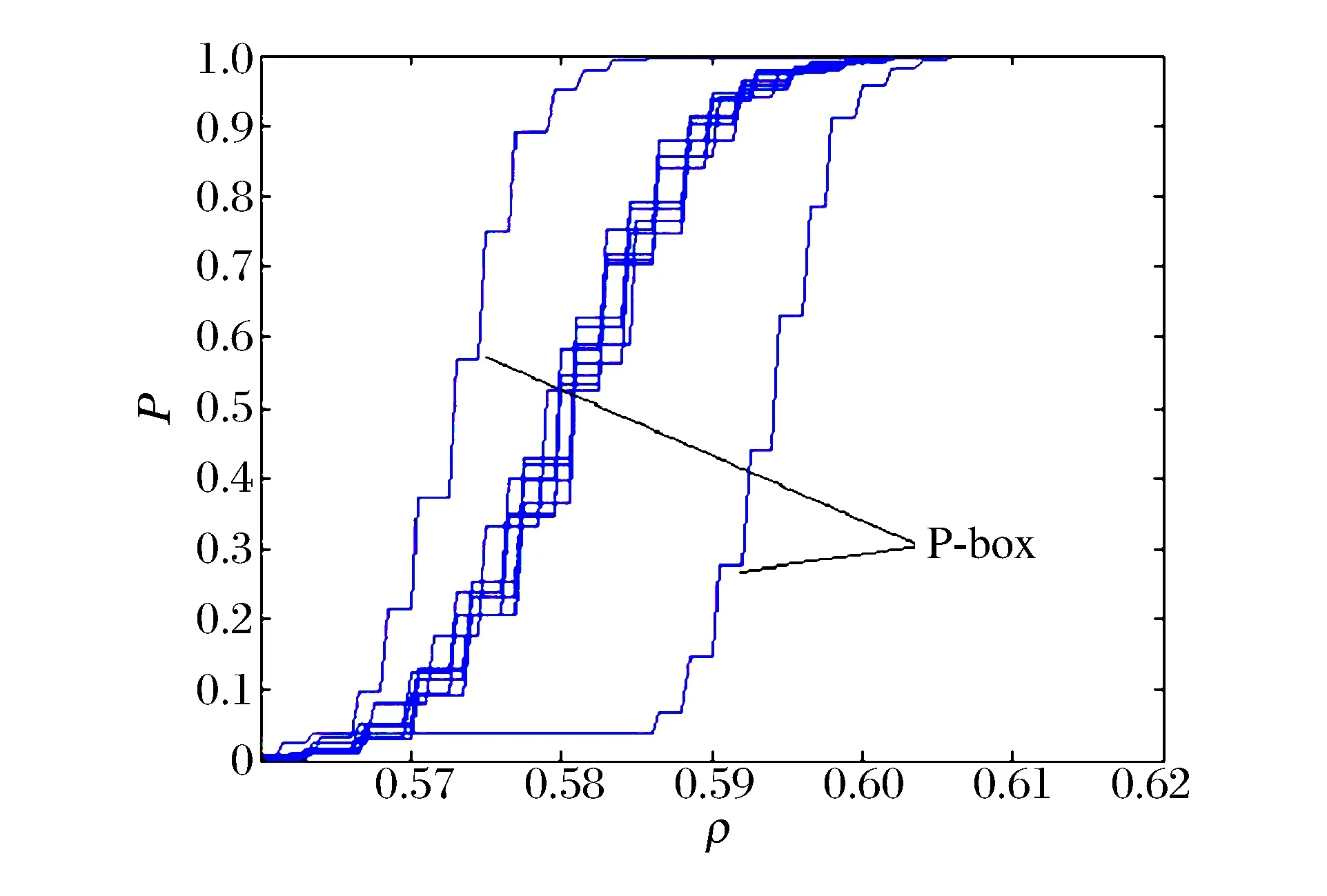
圖6 密度函數的累積分布函數族Fig.6 Cumulative distribution function ensemble of density function

利用第3節中的方法,構造Sod問題中迎風格式的P-box,做出在x=0.1,t=0.22處,密度函數的累積分布函數,如圖6所示,然后選取最內層和最外層概率邊界曲線構成一個P-box,如圖7所示。

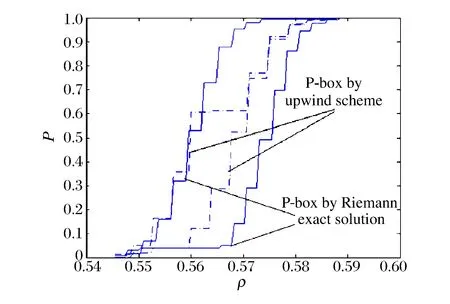
從圖7可以看出，在t=0.22,x=0.1時, 密度ρ(x,t)≤0.555 1的概率0.1

同時,做出黎曼解法器的P-box,并與迎風格式做比較,如圖8所示,不難看出迎風格式構成的P-box基本包含黎曼解法器的P-box,兩者差異不大,這說明采用迎風格式求解Sod問題是有效的。

圖7 利用迎風格式構造的密度函數的P-boxFig.7 P-box constructed by the upwind schemefor density function

圖8 用2種方法構成的密度函數的P-boxFig.8 P-box constructed by two methodsfor density function

5 結 論

(1)流體力學數值模擬過程中初始狀態或輸入條件常含有偶然和認知混合型的不確定性，對模擬結果的響應量有很大影響。

(2)針對流體力學初始狀態中含有偶然不確定性，給出了非嵌入式多項式混沌法量化方法。針對初始狀態中含有認知不確定度，給出了P-box量化方法，提出了一種流體力學輸入參數對模擬輸出響應量不確定性傳播量化的方法。

(3)以迎風格式和黎曼解法器求解Sod問題為例，給出了Sod問題左狀態密度ρL偶然不確定度和多方指數γL認知不確定度，分別采用非嵌入式多項式混沌法和P-box量化結果，給出了流體力學方程組迎風格式數值求解可信度與輸入不確定度的范圍關系，為流體力學數值求解過程中不確定性傳播量化和可信度評估提供了一種有效方法。

[1] Roache P J. Verification of codes and calculations[J]. AIAA Journal, 1998,36(5):696-702.

[2] Staf A A. Guide for the verification and validation of computational fluid dynamics simulations[M]. Reston: American Institute of Aeronautics and Astronautics, 1998:126-180.

[3] American Nuclear Society. Guidelines for the verification and validation of scientific and engineering computer programs for the nuclear industry[M]. ANSI/ANS-10.4-1987, 1987:63-119.

[4] 鄧小剛,宗文剛,張來平,等.計算流體力學中的驗證與確認[J].力學進展,2007,37(2):279-288. Deng Xiaogang, Zong Wengang, Zhang Laiping, et al. Verification and validation in computational fluid dynamics[J]. Advances in Mechanics, 2007,37(2):279-288.

[5] 王瑞利,溫萬治.復雜工程建模與模擬的驗證與確認[J].計算機輔助工程,2014,23(4):61-68. Wang Ruili, Wen Wanzhi. Advances in verification and validation of modeling and simulation of the complex engineering[J]. Computer Aided Engineering, 2014,23(4):61-68.

[6] 劉全,王瑞利,林忠,等.爆轟計算JWL狀態方程參數不確定度研究[J].爆炸與沖擊,2013,33(6):647-654. Liu Quan, Wang Ruili, Lin Zhong, et al. Uncertainty quantification for JWL EOS parameters in explosive numerical simulation[J]. Explosion and Shock Waves, 2013,33(6):647-654.

[7] 劉全,王瑞利,林忠.非嵌入式多項式混沌方法在拉氏計算中的應用[J].固體力學學報, 2013,33(增):224-233. Liu Quan, Wang Ruili, Lin Zhong. Uncertainty quantification for Lagrange computation using non-intrusive polynomial chaos[J]. Chinese Journal of Solid Mechanics, 2013,33(suppl):224-233.

[8] Oberkampf W L, Roy C. Verification and validation in scientific computing[M]. New York: Cambridge University Press, 2010:241-305.

[9] 水鴻壽.一維流體力學差分方法[M].北京:國防工業出版社,1998:225-236.

[10] Xiu Dongbin, Karniadkis G E. The Wiener-Askey polynomial chaos for stochastic differential equations[J]. SIAM Journal on Scientific Computing, 2002,24(2):619-644.

[11] Cameron R H, Martin W T. The orthogonal development of non-linear functionals in series of Fourier-Hermite functionals[J]. Annals of Mathematics, 1947,48(2):385-398.

(責任編輯 張凌云)

Mixed uncertainty quantification and its application in upwind scheme for computational fluid dynamics (CFD)

Liang Xiao1,2, Wang Ruili1

(1.InstituteofAppliedPhysicsandComputationalMathematics,Beijing100094,China;2.CollegeofMathematics,ShandongUniversityofScienceandTechnology,Qingdao266590,Shandong,China)

Both aleatory uncertainty and epistemic uncertainty exist in the initial and boundary conditions when we numerically solve the CFD with sharp discontinuity. In this paper, mixed uncertainty quantification approaches are developed to deal with this situation. Specifically, the outer level uncertainty is linked to epistemic uncertainties, and the inner uncertainty is linked to aleatory uncertainty. The non-intrusive polynomial chaos method is utilized to cope with the aleatory uncertainties, while the P-box theory is used to deal with the epistemic uncertainties, and the upwind scheme and Riemann solver are used to solve the deterministic system. We apply this method to the Sod problem in the CFD, and acquire preferable effect. This method evaluates the influence of input uncertainty such as density (aleatory uncertainty) and polytrophic exponent (epistemic uncertainty) on the output uncertainty, the efficiency of this method is also proved. This method is also helpful in evaluating the degree of confidence and validation of the result from modeling and simulation by other models.

mechanics of explosion; modeling and simulation; non-intrusive polynomial chaos; mixed uncertainty quantification; P-box

10.11883/1001-1455(2016)04-0509-07

2014-12-24；

2015-03-27

國家自然科學基金項目(11372051,11475029);中國工程物理研究院科學基金項目(2015B0202045);山東科技大學人才引進項目(2013RCJJ027)

梁 霄(1984— )，男，博士，講師，mathlx@163.com。

O385國標學科代碼：13035

A