具有最小交易量限制的多階段均值-半方差投資組合優化

張 鵬，張衛國，張逸菲

(1.武漢理工大學經濟學院， 湖北 武漢 430070；2.華南理工大學工商管理學院，廣東 廣州 510641；3.武漢科技大學管理學院，湖北 武漢 430081)

具有最小交易量限制的多階段均值-半方差投資組合優化

張 鵬1，張衛國2，張逸菲3

(1.武漢理工大學經濟學院， 湖北 武漢 430070；2.華南理工大學工商管理學院，廣東 廣州 510641；3.武漢科技大學管理學院，湖北 武漢 430081)

考慮交易成本，借款約束和閾值約束,文章提出了具有最小交易量限制的多階段均值-半方差投資組合模型。該模型是具有路徑依賴性的混合整數動態優化問題,還是NP完全問題。文章提出了前向動態規劃方法求解。最后，通過一個算例比較不同風險約束下的最優投資策略，從而驗證模型和算法的有效性。

多階段投資組合；均值-半方差；最小交易量；借款約束；前向動態規劃方法

1 引言

Markowitz[1-2]提出的均值—方差投資組合理論為現代投資組合的發展奠定了基礎。此后投資多元化問題已經變成了計算問題。Deng Xiaotie等[3]和Hirschberger等[4]提出了基于方差風險度量投資組合模型。雖然方差一直在投資組合中充當風險度量的角色，但其具有一定的局限性[2, 5]。一個明顯的缺點是方差將高收益和低收益同樣認為不好，因為高收益有助于出現極端方差。當證券收益的概率分布是不對稱的，基于方差的投資組合可能犧牲太多的預期收益去消除極端的低收益和高收益，在現實中，許多實證研究,如[6-7]證明了證券收益不是對稱分布的。

為了克服均值-方差模型的局限性，人們開始考慮收益分布的不對稱性。有些學者采用偏態，即三階中心矩來測量收益分布的不對稱性[8-9]，其他學者則直接用下方風險度量，即以負偏差取代方差的度量方法。下方風險度量只關注低于某個預定水平的收益。因此，它符合投資者風險和收益的觀念。實證研究[10]表明投資者大多贊成下方風險度量。Rom和Ferguson[11]研究表明下方風險日益普及。下方風險度量方法有許多形式，安全首要準則[12],半方差[2]。許多學者，如Markowitz等[14]和Huang Xiaoxia[13]研究了半方差的屬性和計算問題。

上述投資組合模型假設投資組合中資產數量為實數，這是不符合實際的。特別是資產都有最小交易量限制(所謂的手)，而解決方案只涉及資產的實數權重，而不涉及資產交易單位。例如，股票手數進行買賣，互惠基金有其各自的最低交易數量。因此，這些模型得到的最優解必須為整數，具有最小交易量的投資組合優化問題是一個組合優化問題(一個NP完全問題)，其可行域是不連續的。一些研究者提出了不同的求解方法，例如Konno和Wijayanayake[15]，Speranza[16]，Mansini和 Speranza[17]， Kellerer等[18]，Lin Changchun和Liu Yiting[19]，Soleimani等[20]，Golmakani和Fazel[21]。

對于上述模型，他們都假設投資期限為一期。但是，在現實生活中，投資組合策略常常是多階段的，因為投資者可以隨時重新分配自己的財富。所以，我們很自然的將單階段投資組合優化擴展到多階段。Mossin[22]運用動態規劃方法求解多階段投資組合模型。Hakansson[23]運用投資組合決策的一般理論方法分析了多階段均值-方差。Li Duan等[24]運用動態規劃的方法來解決多階段安全首要的投資組合問題。用同樣的方法，Li Duan和Ng[25]提出了多階段均值-方差終期財富最大化投資組合模型，并求出了最優投資策略和有效前沿的解析表達式。Calafiore[26]考慮金融資產配置的多階段序貫決策問題，提出了具有線性控制策略的多階段投資組合模型。Zhu Shushang等[27]提出了具有破產風險控制的多階段均值-方差投資組合模型。Gülpnar和Rustem[28]運用情景分析法提出了隨機多階段均值-方差投資組合模型。Yu Mei等[29]提出了具有破產控制的均值-絕對偏差動態投資組合模型。?likyurt和?zekici[30]提出了幾種隨機多階段均值-方差投資組合模型。然而，上述文章多用方差度量風險。在當資產的收益分布不對稱的情況下，利用方差作為風險度量可能會為了消除低收益和高收益極端而犧牲太多的預期收益。為了衡量金融市場中真正的投資風險，學者們采用了一些新的風險度量來取代方差。例如，Yan Wei等[31-32]提出了多階段均值-半方差投資組合模型。Pnar[33]提出了多階段均值—下方風險投資組合模型。Zhang Weiguo等[34-35]和Liu Yongjun等[36-37]提出了多階段模糊投資組合模型，并分別運用遺傳算法，混合智能算法和差分進化算法求解。袁子甲和李仲飛[38]研究了引入參數不確定和學習時的連續時間動態投資組合選擇問題, 使用鞅方法求導出了具有CRRA 型效用函數的投資者的最優投資策略的顯式表達式。金秀等[39]提出了預期效用最大化的動態損失厭惡多階段投資組合優化模型.上面多階段投資組合研究都假設決策變量是連續型變量，實際投資過程中，買賣股票均為整數手(最小交易量)，如中國證券市場規定為100股的整數倍。

文章提出一個新的具有最小交易量限制，借款約束限制和交易成本的多階段均值-半方差投資組合模型。該模型是一個具有路徑依賴的整數動態優化問題。我們提出了前向動態規劃方法求解。

2 多階段均值—半方差投資組合模型

本文討論具有隨機回報的多階段投資組合問題。首先是問題的描述和符號說明，接著描述多階段投資組合的收益和風險，最后提出投資組合模型的最小交易量。

2.1 問題描述和符號說明

假設一個多階段投資組合有n種風險資產和1種無風險資產可供選擇。假設投資者用初始財富W1進行投資，投資者將其財富投資n+1種資產進行T期連續投資，他的財富將在每個時期的開始進行調整。為了方便說明，我們現將所有下文中將使用的符號列在下面。

xit第t期第i種風險資產投資手數的數量，其中xit是整型變量;

xi0第0期第i種風險資產的初始投資的手數;

xt第t期投資組合的手數，其中xt= (x1t,x2t…,xnt);

pit第t期第i種風險資產的單位價格;

Wt第t期的初始財富;

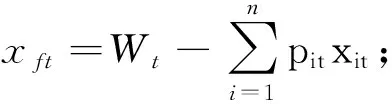
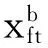
Rit第t期第i種風險資產的隨機收益率;

rit第t期第i種風險資產的期望收益率, 其中rit=E(Rit) ;

rpt第t期投資組合xt的期望收益率;

rNt第t期投資組合xt的凈收益率;

uit第t期第i種風險資產的投資上界;

q第t期第i種風險資產的最小交易量(手)，如中國證券市場規定的100股;

rbt第t期無風險資產的借款利率;

rlt第t期無風險資產的貸款利率;

cit第t期第i種風險資產的單位交易成本;

2.2 多階段投資組合的收益和風險

投資組合中的借款約束是其中的一個影響因素。大多數經紀公司提供從券商借入不同種類的資產進行收購的機會。一些研究人員研究了借款約束，例如，DengXue和LiRongjun[40]提出了具有借貸限制的均值-方差模糊投資組合。Sadjadi等[41]提出了具有不同借款利率和貸款利率的模糊多階段投資組合模型。在實踐中，我們應當考慮到每個資產都有其最小交易量。那么，投資組合優化問題的解必須是整數， t期的投資組合投資數量qxt= (qx1t, qx2t,…, q xnt)′的期望收益為:

(1)

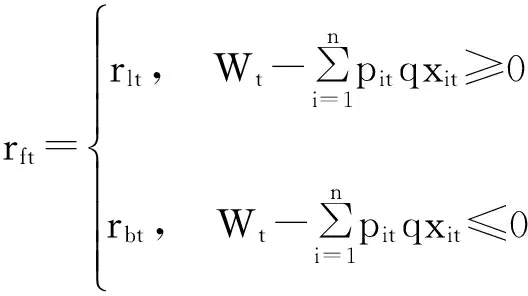
交易成本是投資者關心的主要因素之一。Arnott和Wagner[42]研究發現，忽略交易成本會導致無效投資組合。Yoshimoto[43]的實證分析也得出了同樣的結論。Bertsimas和Pachamanova[44]和Gulpnar等[45]研究了具有交易成本的多階段投資組合問題。我們假設交易成本為第t期投資組合qxt= (qx1t,qx2t…,qxnt)和第t-1期內投資組合qxt-1= (qx1(t-1),qx2(t-1),…,qxn(t-1)) 的V型函數。這就是說，第t期第i種資產的交易成本為cit|pitqxit-pit-1qxit-1|。因此，第t期投資組合xt= (x1t,x2t,…,xnt)的總交易成本可表示為:

(2)

因此，第t期投資組合xt的凈收益可以表示為:

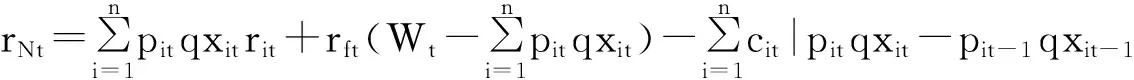
(3)

第t期的借款約束可以寫成:

(4)

那么，第t期的初始財富可以寫成:

(5)

定理1 假設pit表示第t期第i種風險資產的單位價格，q表示第t期第i種風險資產的最小交易量(手)，xit表示第t期第i種風險資產投資手數的數量，其中xt= (x1t,x2t,…,xnt)，則投資組合xt的半方差可以表示為:

(6)

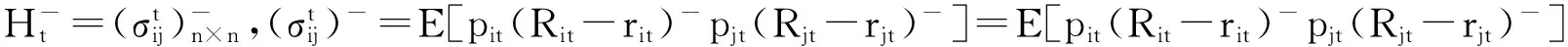
證明：

St(xt)=St(p1tqr1tx1t+p2tqr2tx2t+…+pntqrntxnt)=E{[(p1tqR1tx1t+…+pntqRntxnt)-(p1tqr1tx1t+…+pntqrntxnt)]-}2=E{[q(p1tR1tx1t+…+pntRntxnt)-q(p1tr1tx1t+…+pntrntxnt)]-}2=q2E{[(p1tR1tx1t+…+pntRntxnt)-(p1tr1tx1t+…+pntrntxnt)]-}2=q2E{[(p1t(R1t-r1t)x1t+…+pnt(Rnt-rnt)xnt]-}2

根據Markowitz[2]，上式可以轉化為:

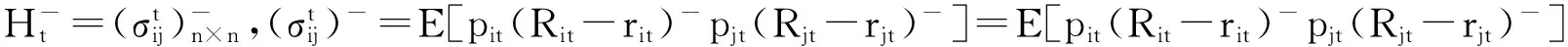
定理證畢。

第t期第i種風險資產的投資上界為:

pitqxit≤zituit

(7)

2.3 具有最小交易量的多階段均值—半方差投資組合模型

假設投資者的目標是在整個T期終期財富最大化。具有最小交易量的多階段投資組合模型為:

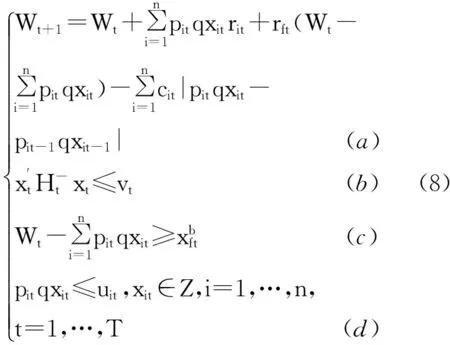
由于模型(8)的可行域是非凸集，該模型不再是凸動態規劃問題。該模型(8)的目標函數是T期投資過程中投資者終期財富最大化。約束條件(a)表示的是財富轉移方程；約束條件((b)表示在任何一個時期內投資組合xt的半方差不超過給定值vt; 約束條件(c)表示第t期無風險資產投資金額的下界限制；約束條件(d)表示xit的上界限制，并且xit是整數值。

在模型(8)中，vtmin≤vt≤vtmax。vtmin和vtmax可以通過以下方法得到：

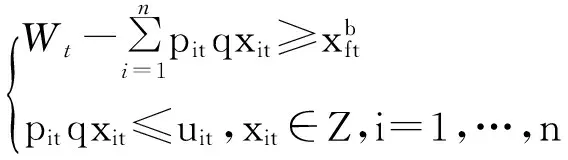
(9)

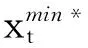
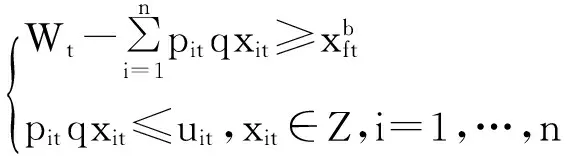
(10)

3 多階段投資組合優化

我們提出了一個前向動態規劃法求解模型(8)。

模型(8)的t期子問題可轉化為:

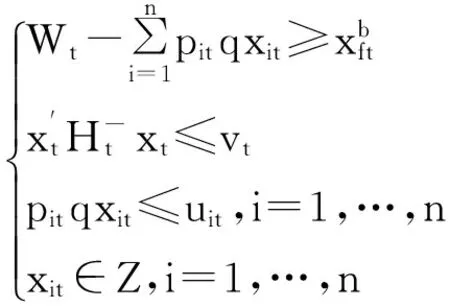
(11)

算法 前向動態規劃方法

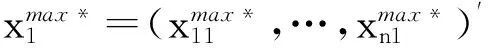
步驟2 如果t=m(m≥1 和mZ+), 由于和已知，運用CPLEX求解模型(11)，也就是說我們已經得到t=m+1的最優解。同時，我們也得到:

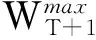
當第t階段決策變量不是太多，運用CPLEX可以求出模型(8)的第t個子問題(11)的全局最優解。因此，運用前向動態規劃也可以求出模型(8)的全局最優解。

4 實證研究

假設投資者從上證權重股中選擇20只股票，分別為S1(600000), S2(600015), S3(600016), S4(600030), S5(600036), S6(600310), S7(600104), S8(600362), S9(600519), S10(600663), S11(6000501), S12(600283), S13(600551), S14(600064), S15(600011), S16(600660), S17(600196), S18(600749), S19(600389), S20(600396)。我們收集了從2006年4月到2013年9月的數據，并且以每三個月為一個周期進行處理。

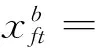
如果在投資組合中借入無風險資產，我們用前向動態規劃方法來解決模型(8)，可以得到如下相應的結果。

當t=1,…,5,我們用CPLEX分別解模型(9)和模型(10)，那么我們得到v1max=0.1203099E+08,v1min=0;v2max=0.1073514E+08,V2min=0;v3max=0.1270018E+08,V3min=0;v4max=0.1515640E+08,V4min=0;v5max=0.1286227E+08,V5min=0。

假設vt=4000000,t=1,…,5,最優解如表1所示。

允許借入無風險資產時，第1期的最優投資策略是x13=1,x41= 96,x91= 14,x131= 133,x161= 201,x171=143,x191=50，其它為0，這意味著投資者應該將他的初始財富分配于資產1, 資產4, 資產9,資產13, 資產16, 資產17, 資產19分別為1, 96,14, 133, 201, 143, 50手， 其他13只股票分配

表1 具有借入無風險資產的多階段投資組合最優解

表2 不含有無風險資產的多階段投資組合最優解

0。從表1還可以得到第2、3、4和5期最優投資策略。終期財富為1766828.4。

如果投資組合不含有無風險資產，模型(8)可轉化為以下模型：

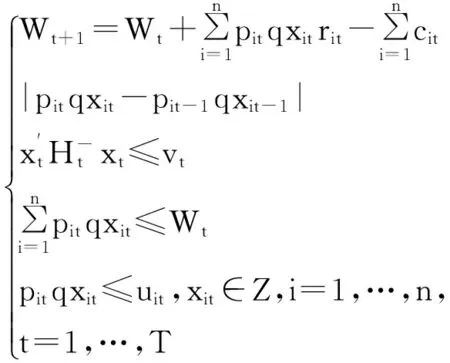
(12)

我們用前向動態規劃方法解決問題(12)，我們可以得到如下的相應結果。

假設vt=4000000,t= 1,…,5,我們可以得到最優解如表2所示。

不含有無風險資產的多階段投資組合的終期財富為1704116。

為了表明無風險資產對于投資組合決策的影響，我們分別考慮了借入無風險資產和不含有無風險資產情況下的投資組合優化問題。運用動態規劃方法求解模型(8)和模型(12)得到相應的最優投資策略如表1和表2所示。從表1 和表2可以看出，當在投資組合決策模型中借入無風險資產，終期財富也隨之變大，這反映了允許借入無風險資產對多階段投資策略有較大的影響。

5 結語

考慮交易成本，最小交易量和借款約束，本文提出了具有風險控制的多階段均值-半方差投資組合模型，該模型為具有路徑依賴的整數動態優化問題。提出前向動態規劃方法求解。最后以一個具體實例比較了不具有無風險借款限制和不含有無風險資產兩種情況下的最優投資策略，驗證了模型和算法的有效性。

與以前多階段投資組合相比，本文研究的多階段投資組合的決策變量是整數與現實投資組合更加符合。對于投資者來說，本文的方法具有良好的可操作性和實用價值。本文結合前向動態規劃方法和CPLEX可以很快地計算出多階段投資組合的最優投資策略。

[1] Markowitz H. Portfolio selection [J]. Journal of Finance, 1952,7(1): 77-91.

[2] Markowitz H. Portfolio selection: Efficient diversification of investments [M]. New York:Wiley, 1959.

[3] Deng Xiaotie, Li Zhongfei, Wang Shouyang. A minimax portfolio selection strategy with equilibrium [J]. European Journal of Operational Research, 2005, 166(1):278-292.

[4] Hirschberger M, Qi Yue, Steuer R E. Randomly generating portfolio-selection covariance matrices with specified distributional characteristics [J]. European Journal of Operational Research, 2007, 177(3): 1610-1625.

[5] Grootveld H, Hallerbach W. Variance vs downside risk: Is there really that much difference? [J]. European Journal of Operational Research, 1999, 114(2):304-319.

[6] Fama E F. Portfolio analysis in a stable paretian market [J]. Management Science, 1965,11(3): 404-419.

[7] Simkowitz M A, Beedles W L. Diversification in a three moment world [J]. Journal of Financial and Quantitative Annals, 1978,13(5): 927-941.

[8] Leung M T, Daouk H, Chen Ansing. Using investment portfolio return to combine forecasts: A multiobjective approach [J]. European Journal Operations Research, 2001,134(1):84-102.

[9] Liu S C, Wang Shouyang, Qiu W H. Mean-variance-skewness model for portfolio selection with transaction costs [J]. International Journal Systems Science, 2003, 34(4):255-262.

[10] Unser M. Lower partial moments as measures of perceived risk: An experimental study [J]. Journal of Economic Psychology, 2000, 21(3):253-280.

[11] Rom B M, Ferguson K W. Post-modern portfolio theory comes of age [J]. Journal of Investing, 1994, 3(3):11-17.

[12] Roy A D. Safety first and the holding of assets [J]. Econometrica, 1952, 20(3): 431-449.

[13] Huang Xiaoxia. Mean-semivariance models for fuzzy portfolio selection [J], Journal of Computational and Applied Mathematics, 2008, 217(1):1-8.

[14] Markowitz H,Todd P,Xu Ganlin,et al. Computation of mean-semivariance efficient sets by the critical line algorithm [J]. Annals of Operations Research, 1993, 45(1): 307-317.

[15] Konno H, Wijayanayake A. Portfolio optimization problem under concave transaction costs and minimal transaction unit constraints [J]. Mathematical Programming, 2001, 89(2): 233-250.

[16] Speranza M G. A heuristic algorithm for a portfolio optimization model applied to the Milan Stock Market [J]. Computers and Operations Research, 1996, 23(5):433-441.

[17] Mansini R, Speranza M G. Heuristic algorithms for the portfolio selection problem with minimum transaction lots [J]. European Journal of Operational Research, 1999, 114(2): 219-233.

[18] Kellerer H, Mansini R, Speranza M G. Selecting portfolios with fixed costs and minimum transaction lots [J]. Annals of Operations Research, 2000, 99(1): 287-304.

[19] Lin Changchun, Liu Yiting. Genetic algorithms for portfolio selection problems with minimum transaction lots [J]. European Journal of Operational Research, 2008,185(1): 393-404.

[20] Soleimani H, Golmakani H R, Salimi M H. Markowitz-based portfolio selection with minimum transaction lots, cardinality constraints and regarding sector capitalization using genetic algorithm[J]. Expert Systems with Applications, 2009, 36(3):5058-5063.

[21] Golmakani H R, Fazel M. Constrained portfolio selection using particle swarm optimization [J]. Expert Systems with Applications, 2011, 38(7): 8327-8335.

[22] Mossion J. Optimal multiperiod portfolio policies [J]. Journal of Business, 1968, 41(2): 215-229.

[23] Hakansson N H. Multi-period mean-variance analysis: Toward a general theory of portfolio choice [J]. Journal of Finance, 1971, 26(4):857-884.

[24] Li Duan, Chan T F, Ng W L. Safety-first dynamic portfolio selection [J]. Dynamics of Continuous, Discrete and Impulsive, Systems Series B: Applications and Algorithms, 1998,4(4): 585-600.

[25] Li Duan, Ng W L. Optimal dynamic portfolio selection: multiperiod mean-variance formulation [J]. Mathematical Finance, 2000,10(3):387-406.

[26] Calafiore G C. Multi-period portfolio optimization with linear control policies [J]. Automatica, 2008, 44(10):2463-2473.

[27] Zhu Shushang, Li Duan, Wang Shouyang. Risk control over bankruptcy in dynamic portfolio selection: a generalized mean-variance formulation [J]. IEEE Transactions on Automatic Control,2004,49(3):447-457.

[29] Yu Mei, Takahashi S, Inoue H, et al. Dynamic portfolio optimization with risk control for absolute deviation model [J]. European Journal of Operational Research, 2010, 201(2):349-364.

[30] ?likyurt U, ?ekici S. Multiperiod portfolio optimization models in stochastic markets using the mean-variance approach [J]. European Journal of Operational Research, 2007, 179(1):186-202.

[31] Yan Wei, Li Shuyong. A class of multi-period semi-variance portfolio selection with a four-factor futures price model [J]. Journal of Applied Mathematics and Computing, 2009, 29(1):19-34.

[32] Yan Wei, Miao Rong, Li Shurong. Multi-period semi-variance portfolio selection: Model and numerical solution [J]. Applied Mathematics and Computation, 2007, 194(1):128-134.

[34] Zhang Weiguo, Liu Yongjun, Xu Weijun. A possibilistic mean-semivariance-entropy model for multi-period portfolio selection with transaction costs [J]. European Journal of Operational Research, 2012, 222(2): 41-349.

[35] Zhang Weiguo, Liu Yongjun, Xu Weijun. A new fuzzy programming approach for multi-period portfolio Optimization with return demand and risk control [J]. Fuzzy Sets and Systems, 2014, 246(1):107-126.

[36] Liu Yongjun, Zhang Weiguo, Xu Weijun. Fuzzy multi-period portfolio selection optimization models using multiple criteria [J]. Automatica, 2012, 48(12): 3042-3053.

[37] Liu Yongjun, Zhang Weiguo, Zhang Pu. A multi-period portfolio selection optimization model by using interval analysis [J]. Economic Modelling, 2013, 33:113-119.

[38] 袁子甲,李仲飛. 參數不確定性和效用最大化下的動態投資組合選擇[J]. 中國管理科學,2010,18(5):1-6.

[39] 金秀,王佳,高瑩. 基于動態損失厭惡投資組合模型的最優資產配置與實證研究[J].2014, 22(5):16-23.

[40] Deng Xue, Li Rongjun. A portfolio selection model with borrowing constraint based on possibility theory [J]. Applied Soft Computing, 2012, 12(2):754-758.

[41] Sadjadi S J, Seyedhosseini S M, Hassanlou Kh. Fuzzy multi period portfolio selection with different rates for borrowing and lending [J]. Applied Soft Computing, 2011, 11(4): 3821-3826.

[42] Arnott R D, Wagner W H. The measurement and control of trading costs [J]. Financial Analysts Journal, 1990, 46(6):73-80.

[43] Yoshimoto A. The mean-variance approach to portfolio optimization subject to transaction costs [J]. Journal of the Operational Research Society of Japan, 1996, 39(1): 99-117.

[44] Bertsimas D, Pachamanova D. Robust multiperiod portfolio management in the presence of transaction costs [J]. Computers and Operations Research, 2008, 35(1):3-17.

Multi-period Mean-semivariance Portfolio Selection with Minimum Transaction Lots Constraints

ZHANG Peng1，ZHANG Wei-Guo2， ZHANG Yi-fei3

(1.School of Economics,Wuhan University of Technology,Wuhan 430070,China;2.School of Business Administration, South China University of Technology, Guangzhou 510641, China;3.School of Management, Wuhan University of Science and Technology, Wuhan 430081, China)

In this paper the multi-period mean semivariance portfolio problem is dealt with minimum transaction lots considering, transaction costs, borrowing constraints and threshold constraints. In this case the problem of finding a feasible solution is NP-complete. An optimal investment policy can be generated to help investors not only achieve an optimal return, but also have a good risk control. The multi-period portfolio selection is the mix integer dynamic optimization problem with path dependence. The forward dynamic programming method is designed to obtain the optimal portfolio strategy. Finally, the comparison analysis with borrowing risk-free assets and without risk-free assets in the portfolio selection is provided by a numerical example to illustrate the efficiency of the proposed approaches and the designed algorithm.

multi-period portfolio selection; mean semivariance; minimum transaction lots; borrowing constraints; the forward dynamic programming method

1003-207(2016)07-0011-07

10.16381/j.cnki.issn1003-207x.2016.07.002

2013-12-29；

2015-01-04

國家自然科學基金資助項目(71271161)；國家社科基金資助項目(13BJL0062)

張鵬(1975-)，男(漢族)，江西吉安人，武漢理工大學經濟學院教授，工學博士，研究方向：投資組合優化、金融工程,E-mail:zhangpeng300478@aliyun.com.

F830

A