長江地鐵隧道地下連續墻施工澆筑數值分析和試驗研究

魏文暉，王寶輝，王志華，王善謠，魏林春

(1.武漢理工大學 道路橋梁與結構工程湖北省重點實驗室，湖北 武漢　430070；2.上海隧道工程股份有限公司，上海　200082)

現澆地下連續墻是地鐵隧道施工中常用的深基坑圍護結構，具有剛度大、整體性好、防滲性強等優點。隨著地下連續墻深度和寬度的逐漸加大，接頭作為整個地下連續墻結構的薄弱環節，其所采用的形式在整個地下連續墻設計中有著重要的影響，其中，H型鋼接頭因其流水線路長、阻力大、止水效果好等優點在地下連續墻設計中得到了普遍采用，并取得了良好的工程效果[1]。然而，H型鋼接頭形式的使用也帶來了一定的問題，即H型鋼在施工澆筑過程中容易出現變形過大[2]，尤其是對于超大、超深的地下連續墻。圖1為地下連續墻澆筑完成后的超聲波檢測圖，過大的H型鋼變形難以保證連續墻之間的咬合，甚至直接影響后幅鋼筋籠的沉槽吊裝，阻礙地下連續墻施工的正常進行。此外，在地下連續墻澆筑過程中，還會出現吊耳鋼筋軸力增大導致鋼筋拉斷的情況，如圖2所示。

目前，大部分針對地下連續墻的研究都集中在地下連續墻施工結束后基坑開挖過程中地下連續墻整體的受力和變形分析[3-15]，鮮有針對施工澆筑過程中地下連續墻受力和變形的研究。因此，施工澆筑過程中地下連續墻H型鋼接頭處變形、吊耳鋼筋受力等關鍵技術問題是地下連續墻施工中亟待研究解決的問題。

圖1地下連續墻超聲波檢測圖2拉斷的吊耳鋼筋

本文利用有限元軟件ANSYS對采用H型鋼接頭的地下連續墻施工澆筑過程進行三維數值分析，研究H型鋼水平變形和吊梁支座反力變化規律，同時以武漢市長江地鐵隧道為研究背景，進行現場試驗研究，并與三維數值分析結果進行對比分析，驗證數值分析方法的合理性和精度，為地鐵隧道地下連續墻施工澆筑工程提供理論和技術支持。

1　工程背景

本文以武漢三陽路長江地鐵隧道工程武昌工作井地下連續墻為研究對象。該工程位于武漢市秦園路下方，工作井平面尺寸為60 m×46 m(長×寬)，圍護采用1.5 m厚C35水下鋼筋混凝土連續墻，接頭形式采用H型鋼接頭，成槽設備采用銑槽機和液壓抓斗成槽機配合施工。地下連續墻的鋼筋籠規格為長56 m，寬5.65 m，厚1.38 m，上部通過由主筋外伸出的吊耳鋼筋懸掛在吊梁上。H型鋼外側填充泡沫高度為56 m，厚度為0.3 m，現澆混凝土高度為h，填充石料高度為L，厚度為0.1 m，土層的相關參數取自相關工程地質勘察報告，地下連續墻澆筑示意圖如圖3所示。

圖3　地下連續墻澆筑示意圖(單位：m)

2　有限元模型

2.1　有限元模型中主要參數的確定

與基坑開挖過程中地下連續墻整體的受力和變形分析不同，地下連續墻澆筑過程中的受力和變形將受到現澆混凝土的直接影響。在澆筑過程中，現澆混凝土將產生收縮變形和凝固，其與鋼筋籠之間的作用也變得更為復雜；同時，在護壁泥漿的影響下，填充石子的物理力學參數也將發生改變。因此，參數的取值、界面接觸的模擬等是否合理，將直接影響三維數值模擬的精確性。

1)現澆混凝土的自生收縮變形

地下連續墻混凝土澆筑時間較長，在此期間混凝土自身會發生一定程度的收縮變形，從而影響H型鋼的變形和吊梁支座反力。因此，選用文獻[16]中建立的自生收縮變形模型進行模擬。該模型綜合考慮了水膠比、礦物摻和料等因素的影響，如式(1)所示。

(1)

在ANSYS分析中，由于混凝土模擬單元SOLID65不具備模擬自生收縮變形的功能，但可以模擬溫度變化產生的變形。因此,本文通過控制混凝土溫度收縮應變使其與混凝土自生收縮應變相同，從而達到模擬混凝土自生收縮變形的效果。

2)現澆混凝土的彈性模量

在澆筑期間，現澆混凝土由于凝結作用，其彈性模量將隨時間的推移而發生變化。因此，采用Kanstad改良彈性模量發展模型[17]進行模擬，如式(2)所示。

(2)

式中：Ect(t)為t時刻混凝土的拉伸彈性模量；Ect,28為混凝土養護28 d的拉伸彈性模量，C35混凝土取3.15×10-2Pa；s為試驗常數，水泥混凝土取0.25；nE為拉伸模量隨時間發展系數，取1.0。

3)填充石料的本構關系

施工澆筑過程中，變形的H型鋼對外側的填充石料將產生明顯的擠壓作用。因此，采用Drucker-Prager屈服準則，描述泥漿影響下填充石料的應力—應變關系，該準則在Mises屈服準則的基礎上考慮了平均主應力對材料抗剪強度的影響，以及因屈服引起的體積膨脹，適用于顆粒狀材料的模擬。

4)現澆混凝土的側向壓力

H型鋼的主要變形是由現澆混凝土的側向壓力引起的。因此，采用雙線性混凝土壓力模型對H型鋼側面施加壓力。雙線性混凝土壓力模型如式(3)所示[18]。

(3)

5)界面接觸問題

地下連續墻澆筑過程中所涉及的界面接觸主要包括：①H型鋼底部砂袋與槽底土體之間的接觸；②填充石料與外側土體之間的接觸。因此采用面—面接觸模型對以上接觸問題進行處理。面—面接觸模型具有能夠傳遞法向壓力和切向摩擦力，不傳遞法向拉力的特點，并支持大滑動和摩擦的大變形，從而可以有效地模擬地下連續墻澆筑過程中的界面接觸。

2.2　基本假定

做如下基本假定：

(1)連續墻施工中，混凝土澆筑速度為勻速；在同一單位時間段(取1 h)內澆筑的混凝土自生收縮變形和彈性模量變化是相同的；

(2)不考慮澆筑過程中混凝土溫度變化產生的應變；

(3)填充石料為連續彈塑性體，采用D—P屈服準則，不考慮其因未壓實而產生的空隙。

2.3　地下連續墻有限元模型

采用不同的有限元模型模擬地下連續墻的各個部分，具體見表1。填充泡沫的彈性模量通過對現場取樣進行單軸壓縮試驗確定，為0.8 MPa。填充石料及場地土層的物理力學參數見表2，其中填充石料的彈性模量及內摩擦角因考慮了泥漿影響而進行了適當弱化。由此建立的地下連續墻有限元模型如圖4所示。

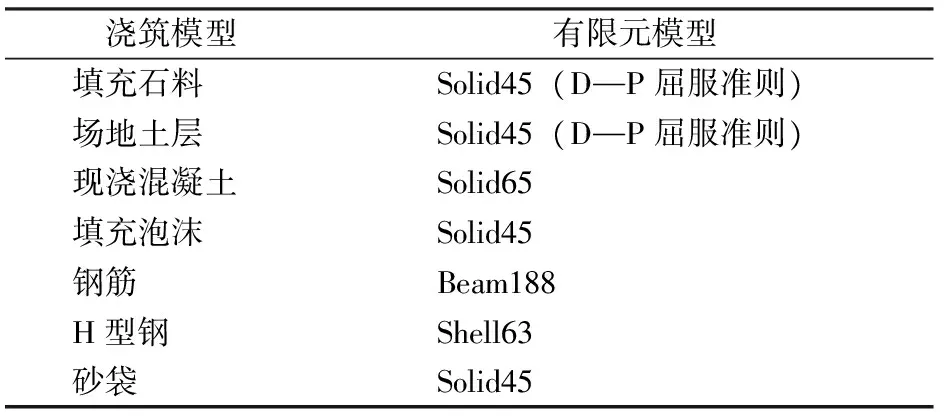
表1　澆筑模型采用的有限元單元

表2　填充石料及場地土層的物理力學參數

圖4　地下連續墻有限元模型

動態施工澆筑過程模擬：①整幅鋼筋籠澆筑過程歷時約為8 h，以每2 h為1個階段將澆筑過程劃分為4個階段；②階段1—階段4的現澆混凝土高度分別為14，28，42，56 m，并考慮不同階段下所澆筑的混凝土由于凝結時間不同而造成混凝土自生收縮變形和彈性模量的差異；③在H型鋼腹板內側面施加相應階段混凝土高度的雙線性混凝土壓力；④結合實際施工中石料填充方案，階段1—階段4的石料填充高度分別為30，40，50，56 m。以此模擬的動態施工澆筑過程如圖5所示。

圖5　動態施工澆筑過程

3　有限元計算結果及分析

從H型鋼水平變形和吊梁支座反力2個方面對地下連續墻澆筑過程中的變形和受力進行分析。

3.1　H型鋼水平變形

為了便于表述H型鋼水平變形隨混凝土澆筑高度變化的規律，將現澆混凝土澆筑高度56 m以每14 m為1個高度段，共劃分為4個高度段，從下至上依次編號為1，2，3，4。澆筑起點和4個高度段終點的相對標高依次為-56，-42，28，-14，0 m。

圖6為有限元計算的各階段下H型鋼的水平變形。從圖6可知：階段1到階段2，H型鋼水平變形在高度段1略有增加，在高度段2內增加較多；階段3，H型鋼水平變形在高度段1和高度段2發生回縮，在高度段3和高度段4之間過渡段(相對標高-21～-7 m)則明顯增加；階段4，H型鋼水平變形在高度段1～高度段3仍出現回縮，在階段3(靠近地下連續墻頂部高度范圍內)有所增大；整個澆筑過程中，H型鋼的最大水平變形始終出現在高度段1內。

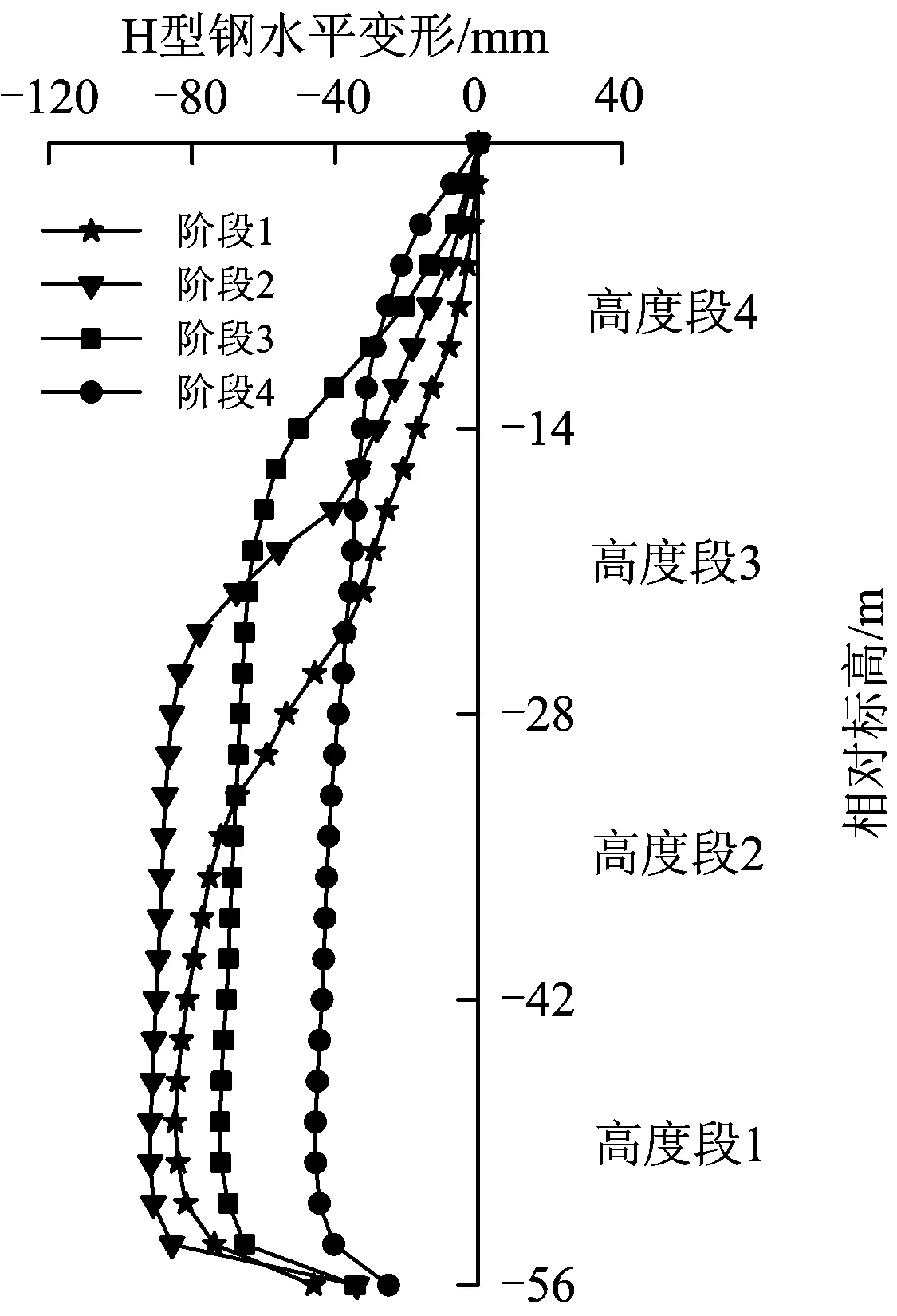
圖6　各階段下H型鋼水平變形

由此可見，H型鋼的最大水平變形在施工澆筑過程初期(階段1、階段2，下同)隨混凝土澆筑高度的增加而增大，在中后期(階段3、階段4，下同)有所減小。究其原因為：一方面是由于在澆筑過程的中后期，混凝土發生的自生收縮，導致H型鋼產生回縮變形；另一方面，隨著混凝土凝結的發展，使得先澆的底部混凝土流動性下降，彈性模量也將相應增大，減少了H型鋼的變形。

3.2　吊梁支座反力

為了便于表述吊梁支座反力隨混凝土澆筑高度變化的規律，對吊梁支座進行編號，如圖7所示。圖8表明了各階段下吊梁各個支座反力隨混凝土澆筑高度變化的規律。

從圖8可知：澆筑過程中，兩側的支座反力變化規律相同；支座反力的最大值始終出現于支座A1(B1)，最小值則始終出現于支座A4(B4)，遠離H型鋼的支座反力大于靠近H型鋼的支座反力，即A1>A2>A3>A4(B1>B2>B3>B4)；階段1到階段2，各吊梁支座反力增大較多；階段3和階段4，支座反力的變化斜率較階段2有所減小。

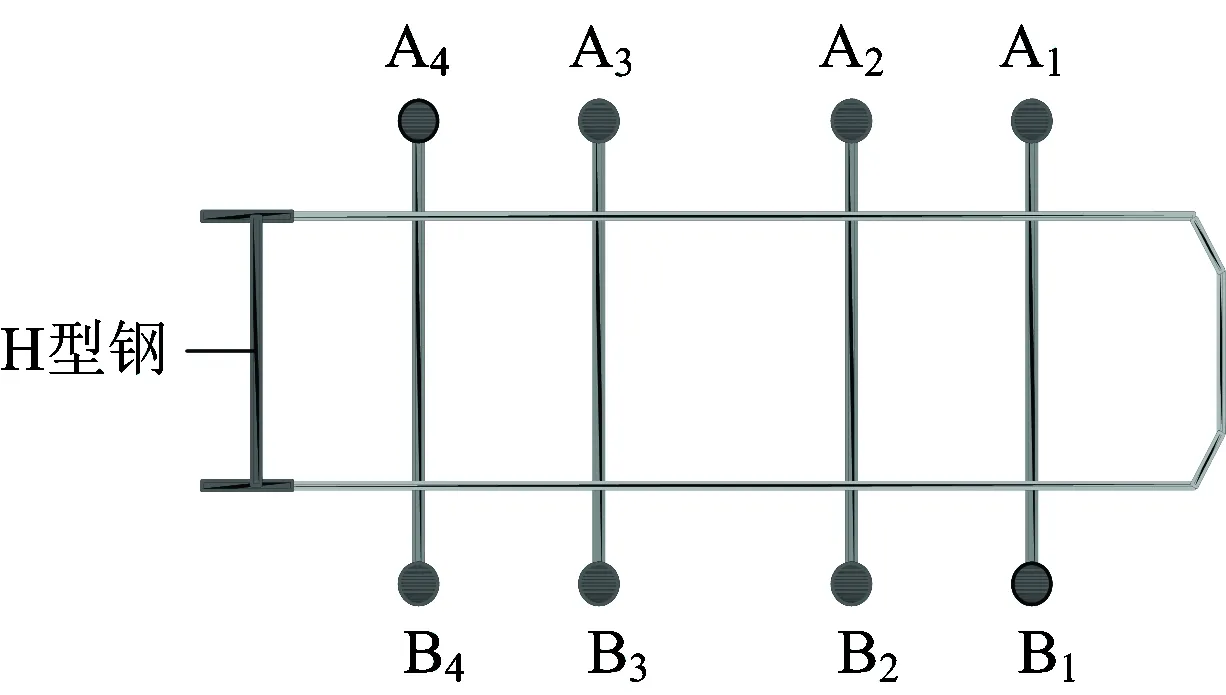
圖7　吊梁支座編號

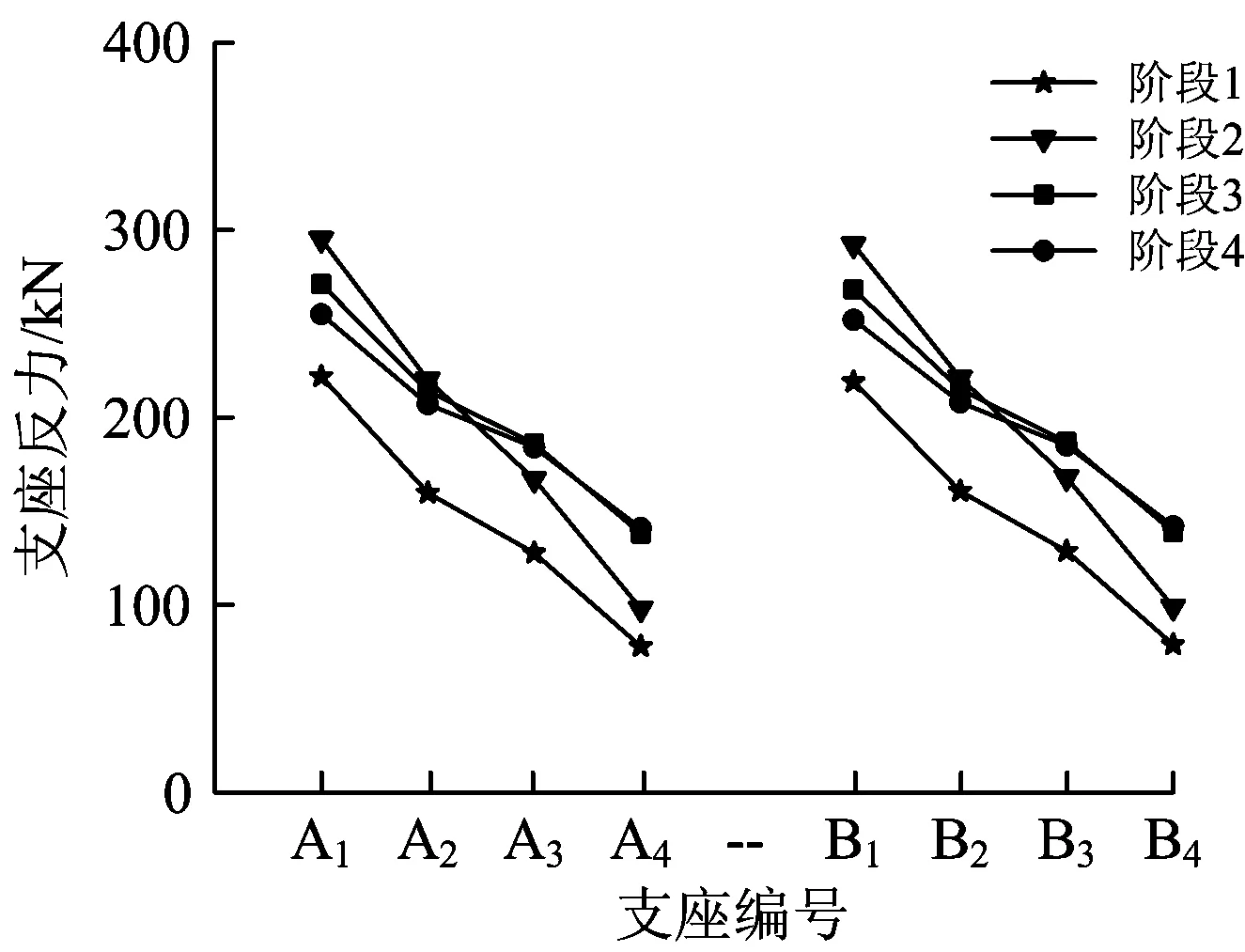
圖8　各階段下吊梁支座反力

圖9為各階段下的吊梁支座總反力(即各支座的反力之和)隨混凝土澆筑高度變化的規律。從圖9可知：隨著混凝土澆筑高度的增加，支座總反力在階段1到階段2為明顯增加，階段2到階段3為略有增加，階段3到階段4則有一定的減小；澆筑過程中，支座總反力的最大值出現于階段3，約為階段1時的1.3倍，并且約為鋼筋籠自身有效重量(885 kN)的2倍。

圖9　各階段下吊梁支座總反力

吊梁支座總反力之所以會出現先增加后緩慢減小的變化規律，主要是因為：在澆筑初期，先澆筑的底部混凝土發生部分凝固且剛度(彈性模量)較低，造成新澆混凝土和底部混凝土的大部分重量通過混凝土與鋼筋之間的粘接作用傳遞到鋼筋籠上部由吊梁承擔，使得支座總反力隨著混凝土澆筑高度的增加而明顯增大，而在澆筑中后期，底部大部分混凝土已經凝固，并且具有較大的剛度，使得混凝土和鋼筋籠的部分重量傳遞到槽底持力層。由于澆筑過程中支座總反力較鋼筋籠自身有效重量高出較多，且現澆混凝土側向壓力引起的彎矩作用會影響支座反力的分布。因此，對此應在施工過程中給以足夠重視，以避免事故發生。

4　現場試驗與有限元分析對比

為了對上述數值分析模型進行驗證，對地下連續墻澆筑過程中的H型鋼水平變形和吊梁支座反力進行了現場試驗。H型鋼水平變形采用美國SLOPE INDICATOR雙向測斜儀量測，如圖10所示，通過讀取固定在H型鋼內側腹板中間測斜儀

圖10　測量H型鋼水平變形的測斜儀

的水平位移來反映H型鋼的水平變形值。吊梁支座反力采用軸力傳感器量測，將軸力傳感器設置于吊梁兩端，如圖11所示。對應4個階段分別統計現場試驗結果。

圖11　測量吊梁支座反力的軸力傳感器

為了能更好地說明施工過程中混凝土的凝結效應(即考慮混凝土自生收縮和彈性模量變化)、泥漿中填充石料的物理力學參數等因素對三維有限元計算結果的影響，除了上節所述的計算結果(定義其為計算1)外，采用上文模型進一步分別對未考慮現澆混凝土凝結效應(即未考慮自生收縮和彈性模量變化)、未考慮泥漿影響的2種情況進行計算，將計算結果分別定義為計算2和計算3，并與現場試驗結果進行對比分析。

4個階段下H型鋼水平變形的計算結果和現場試驗結果對比如圖12所示。由圖12可知：計算1各階段結果與現場試驗結果基本吻合，各高度段無明顯差異(見圖12(a))；計算2明顯大于現場試驗結果，特別是在階段3和階段4時并未發生變形的回縮，與現場試驗結果明顯不符(見圖12(b))；計算3各階段結果明顯小于現場試驗結果(見圖12(c))，表明泥漿影響下填充石料力學參數的取值對于計算結果有較大的影響。

圖12　H型鋼水平變形計算結果與試驗結果的比較

吊梁各支座反力的計算結果與試驗結果對比如圖13所示。由圖13可知：對于各吊梁支座反力，對于計算1，其計算結果與現場試驗結果基本吻合(見圖13(a))；對于計算2，其支座反力的變化斜率大于現場試驗結果，階段3、階段4時在靠近H型鋼一側的支座上出現了“零”反力(見圖13(b))，這是由于H型鋼水平變形過大導致的結果；對于計算3，其支座反力的變化斜率較現場試驗結果略小，且各階段下A1、B1支座反力都小于現場試驗結果(見圖13(c))，這是由于未考慮泥漿影響時H型鋼水平變形較小，對吊梁支座反力分布的影響也較小。

圖13　各吊梁支座反力計算結果與試驗結果的比較

吊梁支座總反力的計算結果與現場試驗結果對比如圖14所示。由圖14可知：階段1—階段4，吊梁支座總反力的計算1和計算3結果與現場試驗結果基本吻合，說明填充石料力學參數的取值對吊梁支座總反力的影響不大。而計算2所得的支座總反力小于現場試驗結果，且在各階段的值幾乎相同，這是因為在有限元分析中將現澆混凝土考慮為理想流體狀態。

圖14　吊梁支座總反力計算結果與試驗結果的比較

以上分析結果證實了考慮混凝土凝結效應和泥漿對填充石料作用的三維有限元計算方法的合理性和準確性，但計算結果與現場試驗結果仍存在一定差異。其原因主要在于：①施工現場環境復雜，填充石料的密實度和泥漿濃稠度難以確定，導致石料的力學參數取值不準確；②本文采用的混凝土自生

收縮模型和彈性模量發展模型是基于常規條件下得到的，本身存在一定誤差，泥漿條件下的相關參數需要進一步研究。

5　結　論

(1)地下連續墻施工澆筑過程中，在現澆混凝土側向壓力和凝結效應的綜合影響下，H型鋼水平變形在施工澆筑過程初期(階段1和2)隨混凝土澆筑高度的增加而增大，在中后期(階段3和4)有所回縮。

(2)施工澆筑過程中，吊梁支座反力的變化較為明顯，澆筑初期隨著混凝土澆筑高度的增加吊梁支座總反力值迅速增加，在澆筑中期略有增加，在澆筑后期出現一定的降低，澆筑過程中總反力最大值約為鋼筋籠有效重量的2倍，且現澆混凝土側向壓力引起的彎矩作用會影響支座反力的分布，在施工過程中應足夠重視，以避免工程事故的發生。

(3)本文計算結果與現場試驗結果基本吻合，說明本文建立的三維有限元模型考慮了施工過程中混凝土的自生收縮變形、彈性模量的變化和泥漿對填充石料的影響，能夠有效地模擬地下連續墻澆筑過程，研究結果可為同類工程施工提供參考和借鑒。

[1]陳懷偉. 杭州地區地下連續墻施工工藝研究[D]. 上海: 同濟大學, 2008.

(CHEN Huaiwei. The Study for Construction Method of Diaphragm Wall in Hangzhou[D]. Shanghai: Tongji University, 2008. in Chinese)

[2]張恒忠. 地下連續墻H型鋼剛性接頭變形的控制措施[J]. 建設監理, 2013(7):70-71.

(ZHANG Hengzhong. Deformation Control Measures of Rigid Joint Used in Diaphragm Wall[J]. Project Management, 2013( 7):70-71. in Chinese)

[3]NG C W W, YAN R W M. Stress Transfer and Deformation Mechanisms around a Diaphragm Wall Panel[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 1998, 124(7): 638-648.

[4]MOHAMMD S Pakbaz，IMANZADEH S，BAGHERINIA K H. Characteristics of Diaphragm Wall Lateral Deformations and Ground Surface Settlements: Case Study in Iran-Ahwaz Metro[J]. Tunnelling and Underground Space Technology, 2013, 35(3): 109-121.

[5]YASUSHI Arai，OSAMU Kusakabe，OSAMU Murata，et al. A Numerical Study on Ground Displacement and Stress during and after the Installation of Deep Circular Diaphragm Walls and Soil Excavation[J]. Computers and Geotechnics, 2008, 35(3): 791-807.

[8]PERLEI E M，RAYUK V F. Use of the Diaphragm Wall Method in Hydrotechnical Construction[J]. Hydrotechnical Construction, 1993,27(11):648-652.

[9]FEDOROV B S，GARAZHA B M. Prospects of Using the Diaphragm Wall Method in Construction[J]. Soil Mechanics and Foundation Engineering,1978,15(1):8-13.

[10]BRUSKOV I V. Analysis of Cast-in-Place Reinforced-Concrete Diaphragm Wall Based on Construction Material[J]. Soil Mechanics and Foundation Engineering，1985, 22(4) :150-152.

[11]LI Kefei，JU Yuwen， HAN Jianguo，et al. Early-Age Stress Analysis of a Concrete Diaphragm Wall through Tensile Creep Modeling[J]. Materials and Structures, 2009,42(7)：923-935.

[12]梅源，胡長明，王雪艷，等. 西安地區濕陷性黃土地鐵車站深基坑開挖引起的地表及基坑支護樁變形特性[J].中國鐵道科學，2016,37(1):9-16.

(MEI Yuan, HU Changming, WANG Xueyan，et al. Deformation Characteristics of Ground Surface and Retaining Pile Induced by Deep Foundation Pit Excavation of Subway Station in Collapsible Loess of Xi’an Area[J]. China Railway Science, 2016, 37(1): 9-16. in Chinese)

[13]徐中華, 王建華, 王衛東. 上海地區深基坑工程中地下連續墻的變形性狀[J]. 土木工程學報, 2008,41(8):81-86.

(XU Zhonghua, WANG Jianhua, WANG Weidong. Deformation Behavior of Diaphragm Walls in Deep Excavations in Shanghai[J]. China Civil Engineering Journal, 2008, 41(8): 81-86. in Chinese)

[14]陳有亮, 李林, 劉井學. 某深基坑地下連續墻開挖變形有限元分析[J]. 地下空間與工程學報, 2008, 4(2): 320-324，330.

(CHEN Youliang, LI Lin, LIU Jingxue. Finite Element Analysis of the Underground Retaining Wall of a Deep Foundation Excavation[J]. Chinese Journal of Underground Space and Engineering, 2008, 4(2): 320-324，330. in Chinese)

[15]楊寶珠，丁克勝，邵強，等. 基于ABAQUS的超深地下連續墻工字鋼接頭型式分析[J]. 地下空間與工程學報, 2014, 10(1): 96-101.

(YANG Baozhu，DING Kesheng，SHAO Qiang，et al. Analysis of H-Steel Joint in Ex-Deep Diaphragm Wall Based on ABAQUS[J]. Chinese Journal of Underground Space and Engineering, 2014, 10(1): 96-101. in Chinese)

[16]張濤. 混凝土早期開裂敏感性的影響因素研究[D]. 北京: 清華大學, 2006.

(ZHANG Tao. Research on the Influence Factors of Concrete Cracking Sensitivity at Early Age[D]. Beijing: Tsinghua University, 2006. in Chinese)

[17]李飛. 混凝土早期約束應力發展與松弛過程研究[D]. 北京: 清華大學, 2009.

(LI Fei. Research on the Development of Restraint Stress and Relaxation of Concrete at Early Age[D]. Beijing: Tsinghua University, 2009. in Chinese)

[18]丁勇春，王建華，褚衍標，等. 地下連續墻施工力學機理三維數值分析[J]. 巖土力學, 2007, 28(8): 1757-1761.

(DING Yongchun，WANG Jianhua，CHU Yanbiao，et al. Three-Dimensional Numerical Analysis Mechanical Behavior of a Constructing Diaphragm Wall Panel[J]. Rock and Soil Mechanics, 2007, 28(8): 1757-1761. in Chinese)