鋼軌磨耗預測模型及其算法的優化

許玉德，魏　愷，孫小輝，陳睿穎

(1.同濟大學 道路與交通工程教育部重點實驗室，上海　201804；2.上海市隧道工程軌道交通設計研究院，上海　200235；3.上海市政工程設計研究總院(集團)有限公司，上海　200092)

磨耗會導致鋼軌的截面面積減小、強度降低，輪軌接觸幾何關系發生變化，影響行車的安全性和舒適性。目前國內外主要將輪軌接觸幾何計算、輪軌滾動接觸理論和輪軌材料磨損模型相結合進行輪軌磨耗的定量預測[1-3]。輪軌接觸幾何計算的研究，從采用簡化的輪軌廓形發展到采用接近真實的輪軌廓形[4-5]，從二維平面的輪軌接觸幾何計算理論發展到考慮車輪搖頭角的三維空間輪軌接觸幾何計算理論[6]，形成了較成熟的跡線法。在輪軌滾動接觸理論方面，Kalker簡化理論(FASTSIM)、沈志云-Hedrick-Elkins小自旋三維滾動接觸理論模型[7]均建立在Hertz接觸理論的基礎上，但是，當輪軌磨耗后(接觸面上存在一定的粗糙)，輪軌接觸條件與Hertz接觸理論的基本假設相悖，因此采用Hertz接觸理論預測輪軌磨耗具有一定的局限性，計算結果誤差較大[8]。目前，非Hertz接觸理論是處理輪軌接觸問題較為準確和完善的理論[9]。

為使輪軌接觸計算準確，本文將非Hertz滾動接觸理論應用于鋼軌磨耗預測模型中；另外，針對用傳統算法更新鋼軌廓形所形成的“毛刺”問題，提出網格拓展的優化算法，以消除“毛刺”問題，使鋼軌磨耗的預測結果更加準確，并將預測結果與實測結果進行對比，以驗證鋼軌磨耗預測模型和優化算法的準確性。

1　鋼軌磨耗預測模型

1.1　鋼軌磨耗計算主要流程

將車輛—軌道動力學仿真[10]、非Hertz接觸理論和能量耗散磨耗模型相結合，對鋼軌磨耗進行計算和分析，主要流程如圖1所示。

圖1　鋼軌磨耗計算主要流程

1.2　車輛—軌道動力學仿真模型

采用Simpack多體動力學仿真軟件建立車輛—軌道動力學仿真模型[7]，其拓撲結構如圖2所示。模型由車輛、軌道兩部分組成，車輛模型由車體、搖枕、側架和輪對組成，且均視為剛體[8]；軌道結構簡化為板式軌道模型，鋼軌和軌道板之間采用剛性連接，軌道板和剛性基礎之間采用彈性連接。

圖2　車輛—軌道動力學仿真模型的拓撲結構

1.3　輪軌非Hertz滾動接觸模型

根據Kalker的非Hertz接觸理論，對鋼軌可能接觸的區域進行網格離散，用正交網格將軌面劃分為矩形單元格，如圖3所示。圖中：xyz坐標系的原點o置于軌頭中心線上；Δx和Δy分別為網格單元在x向和y向的長度。

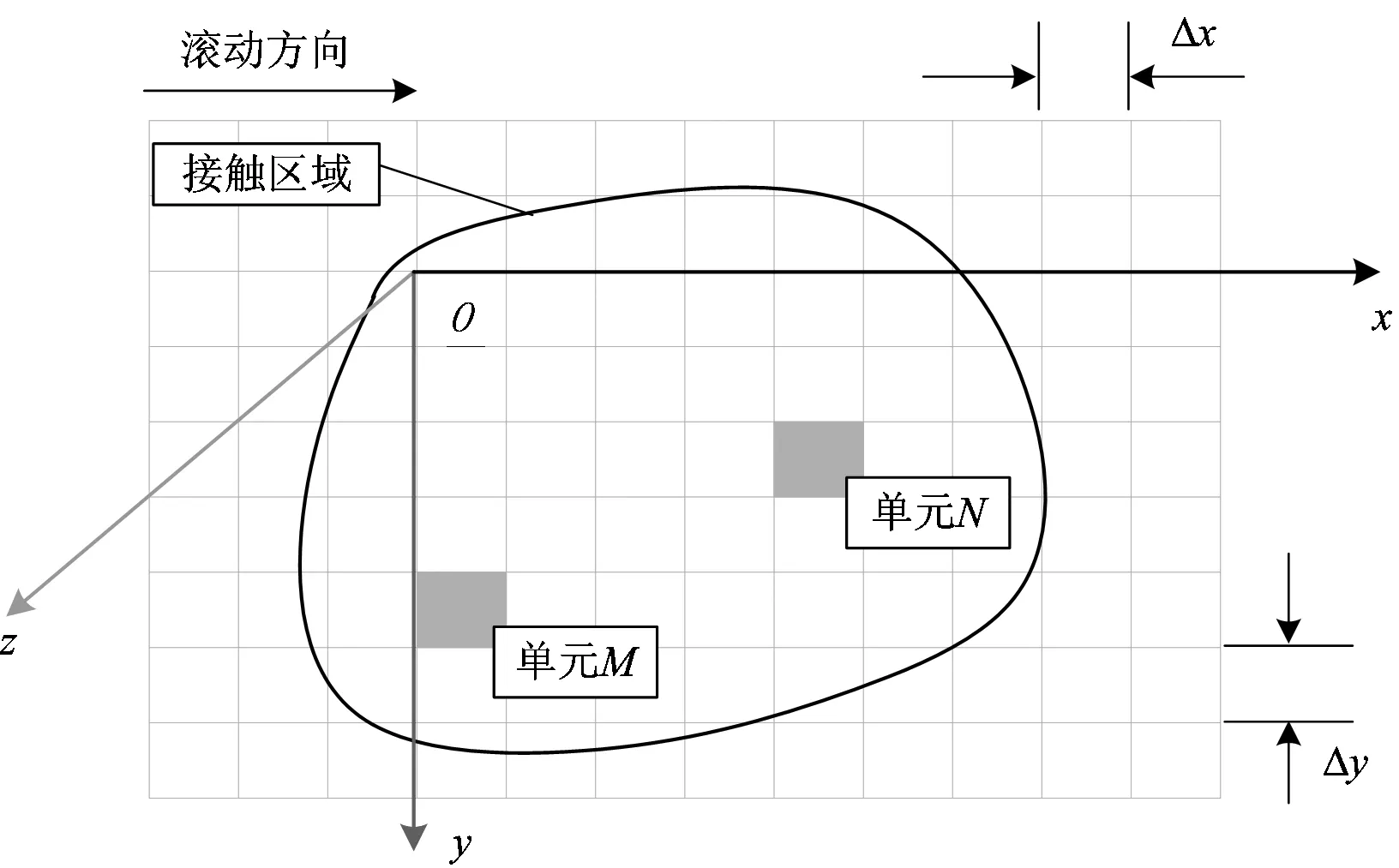
圖3　鋼軌可能接觸區域的網格離散

鋼軌接觸斑上的法向應力和切向應力滿足式(1)。

s.t.

σMz≥0

|σMg|≤bM

?M∈C

(1)

其中，

S=ΔxΔy

按照式(1)對輪軌接觸時的法向和切向應力進行求解。

1.4　鋼軌材料磨損模型

(2)

其中，

P(xM，yM，t)=σMxv0

(3)

(4)

(5)

式中：a為車輪通過網格單元M的過程中所經過的網格數量。

2　數值方法的優化和驗證

2.1　優化算法

在輪對初次通過鋼軌時，其接觸斑內的離散網格能覆蓋全部接觸斑，但輪對通過一定次數后，由于鋼軌磨耗的發展，其接觸斑沿橫向向兩邊擴展。由于按照傳統的基于非Hertz接觸理論的算法(簡稱傳統算法)，網格單元劃分后是固定不變的，因此當實際接觸斑超過網格離散區域后，繼續按照之前的離散網格單元進行鋼軌磨耗計算，預測出的鋼軌型面就會顯現出被磨出的“臺階”。此后，隨著磨耗的疊加將在臺階內和臺階兩側出現更多的臺階，也就是預測出的鋼軌型面會顯現出“毛刺”。因此，本文采用在鋼軌磨耗疊加的過程中逐步擴展離散區域的優化算法，使離散區域總是能覆蓋全部的接觸斑。

假設接觸斑的擴展是連續的，則在輪軌滾動接觸計算中若發現矩形離散區域的邊界上存在法向力，說明接觸斑已經延伸到了離散區域的邊界，此時就應擴展離散區域的邊界。優化算法如圖4所示。

2.2　準確性驗證

Kalker的非Hertz接觸理論有其相應的數值程序CONTACT，但該程序難以實現大量、重復的計算。因此本文在Matlab軟件中采用不動點迭代的方法實現非Hertz接觸理論的數值計算。

數值計算工況的參數見表1。

按照本文提出的優化算法計算鋼軌接觸區域的參數，并與CONTACT軟件中用傳統算法計算的結果進行對比，見表2。

從表2可以看出：優化算法與傳統算法的各項計算結果均較為接近，證明優化算法的可靠性。

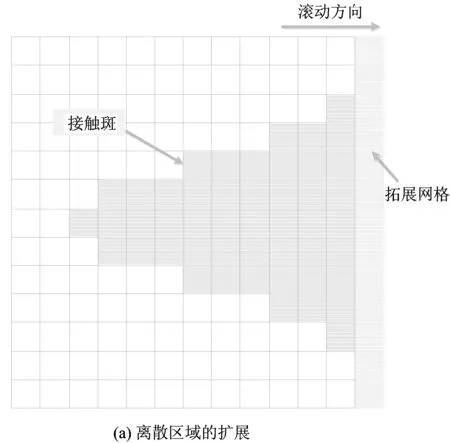
圖4　優化算法

參數名稱參數取值剪切模量/GPa82泊松比03法向力/kN100縱向蠕滑率10-3橫向蠕滑率10-4自旋蠕滑率/(rad·mm-1)2×10-5輪對前進速度/(m·s-1)20單元格面積/mm208×08

3　重載鐵路鋼軌磨耗預測結果

選取國內某重載鐵路曲線段進行鋼軌型面磨耗的預測，該曲線段建立了觀測段，有實測數據作為驗證依據。曲線參數見表3。

表2　優化算法與傳統算法計算結果的對比

表3　實測重載鐵路曲線軌道參數表

3.1　預測結果的對比分析

采用傳統算法和優化算法，分別計算得到的輪對通過不同次數時鋼軌的磨耗量如圖5所示。

圖5　輪對通過不同次數時鋼軌的磨耗量

從圖5可以看出：鋼軌磨耗時的接觸斑沿橫向擴展，這是由于磨耗發展過程中鋼軌型面不斷變化，輪軌接觸點附近的鋼軌表面被“磨平”，趨向于與車輪踏面的共形化，這就導致鋼軌接觸斑的面積變大[12]；采用傳統算法進行鋼軌磨耗預測的過程中出現了較為明顯的毛刺，而采用優化算法時在增加了離散網格的擴展機制后，鋼軌磨耗的預測結果較為平滑，表明優化算法的計算結果更為準確。

3.2　預測結果的驗證分析

根據預測結果，外軌圓曲線中點鄲鋼軌型面上各處通過不同車輛總重時的磨耗如圖6所示。圖中橫坐標為負時指向工作邊，為正時指向非工作邊。

圖6　外軌圓曲線中點處通過不同車輛總重時的磨耗量

從圖6可以看出：鋼軌磨耗最初分布在距離軌頂面中心-26～0 mm弧長范圍內，之后分別向兩邊擴展，其中向鋼軌非作用邊的擴展量較大。

為驗證鋼軌磨耗預測的準確性，將外軌圓曲線中點處的磨耗量的預測值與實測值進行比較，如圖7所示。

圖7　外軌圓曲線中點處磨耗量的預測值與實測值比較

從圖7可以看出：二者的吻合程度較高，但仍有部分差異，表現為預測值的增長是勻速增長趨勢，而實測值的增長是先快速后穩定；這一方面是由于實際工況下重載鐵路新軌表面存在脫碳層，硬度較低，磨耗發展較為迅速，而計算工況時未對其進行模擬；另一方面是由于磨損系數會隨著法向應力的增加而陡增，而計算工況無法與實際工況完全相同。

4　結　語

(1)在現有車輛—軌道多體動力學、輪軌滾動接觸力學和材料摩擦磨耗模型的基礎上，在輪軌接觸中采用輪軌非Hertz接觸理論建立鋼軌磨耗預測模型。

(2)提出在輪軌滾動計算時離散區域隨法向力擴展的優化算法，并與傳統算法進行了對比和驗證，結果相差不超過7%，驗證了優化算法的可靠性。

(3)對比采用優化算法和傳統算法對某重載鐵路曲線段鋼軌磨耗進行預測，并將預測結果與實測結果進行對比，表明優化算法有效減少了鋼軌磨耗的“毛刺”現象，且其預測結果與實測結果的吻合程度較高。

[1]李霞，溫澤峰，金學松.重載鐵路車輪磨耗和滾動接觸疲勞研究 [J]. 鐵道學報，2011，33(3)：28-34.

(LI Xia，WEN Zefeng，JIN Xuesong. Investigation into Wheel Wear and Fatigue of Heavy Haul Railways[J].Journal of the China Railway Society，2011，33(3)：28-34. in Chinese)

[2]李霞.車輪磨耗預測初步研究 [D]. 成都：西南交通大學，2009.

(LI Xia. Preliminary Study on the Prediction of Wheel Wear[D].Chengdu：Southwest Jiaotong University，2009. in Chinese)

[3]LI Xia，JIN Xuesong，WEN Zefeng，et al. A New Integrated Model to Predict Wheel Profile Evolution Due to Wear[J].Wear， 2011，271(1)： 227-237.

[4]王開文.車輪接觸點跡線及車輪接觸幾何參數的計算 [J]. 西南交通大學學報， 1984，19 (1)： 89-98.

(WANG Kaiwen. The Track of Wheel Contact Points and the Calculation of Wheel/Rail Geometric Contact Parameters[J].Journal of Southwest Jiaotong University，1984，19(1)： 89-98. in Chinese)

[5]嚴雋耄.具有任意輪廓形狀的輪軌空間幾何約束的研究[J].西南交通大學學報，1983，18(3)：40-47.

(YAN Junmao. A Study on Wheel/Rail Spatial Geometric Constraints for Arbitrary Wheel and Rail Profiles[J]. Journal of Southwest Jiaotong University， 1983 ，18(3)： 40-47. in Chinese)

[6]張衛華.空間狀態輪輪(軌)接觸點計算方法 [J]. 中國鐵道科學，2006，27(4)：76-79.

(ZHANG Weihua. Calculation Method of Wheel/Roller(Rail)Spatial Contact Point[J].China Railway Science，2006，27(4)：76-79. in Chinese)

[7]金學松，劉啟躍.輪軌摩擦學 [M]. 北京：中國鐵道出版社，2004.

[8]孫樹磊，丁軍君，黃運華，等.鐵路貨車參數對車輪磨耗影響的仿真研究 [J]. 中國鐵道科學，2013，34(5)：100-107.

(SUN Shulei，DING Junjun，HUANG Yunhua，et al. Simulation Study on the Effect of Railway Freight Car Parameters on Wheel Wear [J]. China Railway Science，2013，34(5)：100-107. in Chinese)

[9]KALKER J J.三維彈性體的滾動接觸 [M]. 成都：西南交通大學出版社，1991.

[10]翟宛明. 車輛—軌道耦合動力學 [M]. 北京：科學出版社，2003.

[11]丁軍君，李芾，黃運華. 基于蠕滑機理的車輪磨耗模型分析 [J]. 中國鐵道科學，2010，31(5)：66-72.

(DING Junjun，LI Fu，HUANG Yunhua. Analysis of the Wheel Wear Model Based on the Creep Mechanism [J]. China Railway Science，2010，31(5)：66-72. in Chinese)

[12]LEWIS R,OLOFSSON U. Mapping Rail Wear Transitions[J]. Wear,2004,257(3):721-729.

[13]肖乾， 黃碧坤， 徐紅霞，等. 不同運行工況下高速輪軌穩態滾動接觸蠕滑特性分析[J]. 中國鐵道科學， 2015， 36(3): 81-87.

(XIAO Qian， HUANG Bikun， XU Hongxia，et al.Creep Characteristics of High Speed Wheel-Rail Steady-State Rolling Contact under Different Operation Conditions[J]. China Railway Science，2015， 36(3): 81-87. in Chinese)

[14]宋華， 楊建， 張月， 等. 非線性穩態曲線通過時輪軌滾動接觸的數值求解方法[J]. 中國鐵道科學， 2015， 36(5): 80-86.

(SONG Hua， YANG Jian， ZHANG Yue， et al.Numerical Solution Method for Wheel-Rail Rolling Contact of Nonlinear Steady-State Curve Negotiating [J]. China Railway Science，2015，36(5):80-86. in Chinese)