模型思想在解決問題教學(xué)中的運用

江蘇鹽城市中興實驗學(xué)校（224000）徐　娟

?

模型思想在解決問題教學(xué)中的運用

江蘇鹽城市中興實驗學(xué)校（224000）徐娟

［摘要］數(shù)學(xué)模型思想的運用是學(xué)生體會和理解數(shù)學(xué)與外部世界聯(lián)系的基本途徑。教師若能把模型思想滲透于解決問題教學(xué)中，則不僅可以優(yōu)化學(xué)生的解題思路，而且可以顯著提升教學(xué)效果。

［關(guān)鍵詞］小學(xué)數(shù)學(xué)數(shù)學(xué)模型思想解決問題教學(xué)運用

數(shù)學(xué)模型是用數(shù)學(xué)語言概括或近似地描述現(xiàn)實世界事物的特征、數(shù)量關(guān)系以及空間形式的一種數(shù)學(xué)結(jié)構(gòu)。解決問題作為學(xué)生的重要學(xué)習(xí)內(nèi)容，教師要注重在其中滲透模型思想。經(jīng)常進行利用模型思想解決問題的練習(xí)，對于提升學(xué)生解題能力、增強其應(yīng)用意識具有顯著促進作用。下面我就模型思想在解決問題教學(xué)中的具體運用談?wù)勛约旱慕虒W(xué)體會。

一、借助情境，從“生活原型→數(shù)學(xué)模型”，感知數(shù)學(xué)模型思想

在解決問題教學(xué)中，許多問題與學(xué)生的日常生活關(guān)系密切。教師可從學(xué)生已知的生活原型入手創(chuàng)設(shè)恰當(dāng)?shù)那榫常箤W(xué)生在生活情境的觸發(fā)下把抽象的數(shù)學(xué)問題轉(zhuǎn)化為數(shù)學(xué)模型，并應(yīng)用數(shù)學(xué)模型思想來解決具體問題，從而提高學(xué)習(xí)效果。

如教學(xué)“平均分”時，我創(chuàng)設(shè)了這樣一個學(xué)習(xí)情境：體育課上，老師拿來一些跳繩讓學(xué)生（共54人）練習(xí)，請問這些跳繩應(yīng)該如何分配？經(jīng)過思考，學(xué)生認為這道題沒有告知跳繩的具體數(shù)量，沒辦法分。此時，教師趁機追問：“怎樣才能知道跳繩的總數(shù)？如果讓你來分，你會怎樣分？”在教師的追問下，學(xué)生說：“首先要數(shù)一數(shù)跳繩的總數(shù)，然后再根據(jù)學(xué)生人數(shù)進行平均分，這樣才公平合理。”教師通過“創(chuàng)設(shè)問題情境→提出方法→平均分→公平合理”的學(xué)習(xí)過程，有效地促進了學(xué)生對“平均分”這一概念的認識。

由上述教學(xué)案例可以看出，生活情境的創(chuàng)設(shè)能喚醒學(xué)生的已有知識和經(jīng)驗，使其真正經(jīng)歷數(shù)學(xué)知識從生活原型到數(shù)學(xué)模型的形成過程，幫助學(xué)生初步感知數(shù)學(xué)模型思想的應(yīng)用。

二、引導(dǎo)發(fā)現(xiàn)，從“分析比較→抽象綜合”，建立數(shù)學(xué)模型思想

在解決問題教學(xué)中，除借助情境幫助學(xué)生感知數(shù)學(xué)模型外，教師還要善于引導(dǎo)學(xué)生進行分析和比較，提取有價值的信息，并綜合運用到解題過程中。這樣教學(xué)，有助于學(xué)生快速建立起相應(yīng)的數(shù)學(xué)模型，發(fā)現(xiàn)解決問題的具體策略。

如在“圓的面積”的課后練習(xí)中有這樣一道題：

下面三個正方形的邊長都是3厘米，涂色部分的面積相等嗎？為什么？

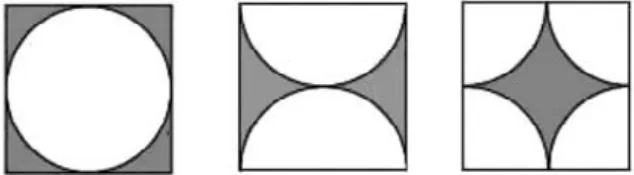
剛看完題目時，學(xué)生習(xí)慣性地想運用圓的面積公式來解答。但仔細讀題后，學(xué)生發(fā)現(xiàn)這個方法不可行。于是我讓他們觀察、比較這些圖形，思考它們的空白部分有什么特點、要求涂色部分的面積除了常規(guī)的直接求解方式外還有什么方法。在我的提示下，學(xué)生經(jīng)過觀察、分析和思考，建立起“涂色部分面積＝正方形面積—空白部分面積”這個關(guān)系模型。

在上述解決問題的教學(xué)案例中，教師沒有直接把解題的方法告知學(xué)生，而是在引導(dǎo)學(xué)生仔細觀察圖形的基礎(chǔ)上，鼓勵學(xué)生自己去分析這些圖形的異同點。這樣教學(xué)，從分析比較到抽象綜合，使學(xué)生親歷數(shù)學(xué)模型的建立過程，能強化學(xué)習(xí)效果。

三、探尋本質(zhì)，從“表述過程→分享經(jīng)驗”，深化數(shù)學(xué)模型思想

在學(xué)生的數(shù)學(xué)學(xué)習(xí)中滲透模型思想的根本目的是讓學(xué)生在探尋數(shù)學(xué)規(guī)律的過程中發(fā)現(xiàn)知識的本質(zhì)特點，幫助學(xué)生學(xué)會運用模型思想來解決具體問題。因此，教師要在幫助學(xué)生在探尋知識本質(zhì)、建構(gòu)數(shù)學(xué)模型的基礎(chǔ)上，更有效地把握解題策略，深化數(shù)學(xué)模型思想。

如“百分數(shù)的認識”的課后練習(xí)中有這樣一道習(xí)題：

從題目可以看出，教材先從簡單的“百分之幾”這個數(shù)學(xué)模型入手，隨后又啟發(fā)學(xué)生從藥品市場抽檢合格率的變化情況談?wù)勛约旱恼J識。教師若順應(yīng)教材的設(shè)計思路，引導(dǎo)學(xué)生表述自己的解題思路與想法、分享學(xué)習(xí)成果，可促進學(xué)生發(fā)現(xiàn)知識的本質(zhì)與規(guī)律。當(dāng)學(xué)生真正探尋到解決問題的本質(zhì)與規(guī)律時，他們就不只學(xué)會了解決問題，更積累了基本的模型構(gòu)建經(jīng)驗，深化了對數(shù)學(xué)模型思想的認識。

數(shù)學(xué)教師要善于引導(dǎo)學(xué)生在解決問題的過程中構(gòu)建數(shù)學(xué)模型，鼓勵學(xué)生將之進行內(nèi)化并遷移運用，從而提高學(xué)生的思維能力，為學(xué)生的終身發(fā)展奠定基礎(chǔ)。

（責(zé)編吳美玲）

［中圖分類號］G623.5

［文獻標識碼］A

［文章編號］1007-9068（2016）05-048