問題驅動:從此岸走向彼岸——以“和與積的奇偶性”為例
江蘇海安縣實驗小學(226600)顧 榮
?
問題驅動:從此岸走向彼岸——以“和與積的奇偶性”為例
江蘇海安縣實驗小學(226600)顧榮
[摘要]教師將學習的目標問題化,讓新知學習成為一個項目研究,促使學生發現問題、提出問題、分析問題、解決問題。以問題激發學習動機,彰顯學生主體地位;以問題聚焦學習內容,凸顯學習目標;著力問題解決,培養探究能力;圍繞問題展示,促進良性互動;強化反思梳理,發展元認知能力。
[關鍵詞]問題問題解決探究能力數學素養
學生的認知發展過程是一個不斷將未知轉化成已知的過程。未知領域的知識有可能是“要求回答或解釋的題目”,也可能是“需要研究討論并加以解決的矛盾、疑難”。在教學過程中,教師可以將這些未知知識教授給學生,也可以將其轉化為一個又一個“問題”讓學生去研究、探索,讓學生在解決問題的過程中掌握新知。在小學數學學習過程中,許多未知的數學知識都可以看做是學生需要解決而未解決的問題,包括擺在學生面前需要掌握的新知識,需要不斷完善的認知結構,解決數學問題必備的方法技能,以及學生需要自我關照的元認知能力,等等。這些問題會讓學生產生一種對學習內容的不解的認知狀態,這樣的狀態使教學形成了強大的張力。因此教師要突出“問題”的作用和地位,教學全程都要體現知識問題化、目標問題化的理念,追求“問題”為主線的教學,用問題來驅動教學。將學習內容創設成系列的、環環相扣的問題,用問題激發學生學習數學的原動力,能把學生的思維引向深處,從而最大限度地激發他們體驗和理解數學學習內容的本質,形成良好的數學素養。下面以“和與積的奇偶性”教學為例談談個人的實踐和思考。
一、破題,用問題指引方向
師:明天我們將研究“和與積的奇偶性”,看到這個課題,你會提出哪些問題?你會想到哪些相關知識?
生1:與加法有關,與乘法有關。
生2:與奇數、偶數有關。
師:能具體說說你的猜想嗎?
生3:就是研究加法中的和是奇數或偶數的情況,乘法中的積是奇數或偶數的情況。
師:加法也好,乘法也好,都有簡單與復雜之分,你將采取怎樣的研究策略呢?
生4:先研究兩個數相加的和的奇偶性,接著研究三個數連加的和的奇偶性,再研究四個數、五個數連加的情況……乘法也是這樣,先簡單再復雜。
師:還有什么問題嗎?
生5:和與積的奇偶性有怎樣的規律,和的奇偶性的規律與積的奇偶性的規律有什么聯系和區別?
師:其實我們要研究的一個核心問題就是——和與積的奇偶性有怎樣的規律?請大家將這個問題作為研究的課題,回家完成課前導學單。
【思考:教師將學習的目標問題化,讓新的學習成為一個項目研究,促使學生發現問題、提出問題,尋求到研究的大致方向,從而為學生的研究探索聚焦。】
二、導學,用問題規劃方案
1.試一試,我能行
(1)兩個數相加,什么情況下和是奇數?什么情況下和是偶數?你能舉出一些合適的例子來研究其中的規律嗎?
通過研究,我的發現是()
(2)幾個數連加,你又是怎樣研究的?你有什么困惑嗎?
我重點研究的是()個數連加
我的發現是()
我想提醒大家的是()
我的困惑有()
2.說一說,我收獲
把你的發現說給爸爸媽媽聽,再聽聽他們的意見,對自己的理解會有幫助哦!
3.做一做,我超越
(1)連續10個自然數的和是奇數還是偶數?連續40個奇數的和呢?
我是這樣想的()
(2)學校車棚里有一些自行車和三輪車,輪子的總數和車輛數都是奇數,那么自行車的輛數是奇數還是偶數?三輪車的輛數呢?(建議將自己的思考過程通過適當的方式展示出來)
【思考:課前問題導學,將學習內容進行問題化、板塊化、方案化的處理,聚焦于教學的核心內容,這樣有利于學生分析問題和解決問題能力的發展。本課題的研究內容主要是和的奇偶性和積的奇偶性。課前的導學單上,主要出現的是和的奇偶性的研究內容,這是教者精細設計的,因為和的奇偶性的研究較為復雜,需要從簡到繁不斷推進,而積的奇偶性可以在和的奇偶性的基礎上實現遷移。因此,導學單上將學習內容以問題的形式設計了三個層次:一是用舉例的方法研究兩個數相加的和的奇偶性;二是選擇性地研究連加的和的奇偶性;三是揭示和的奇偶性的規律。這樣的問題具有方案性,使學生的研究從簡到繁,既有利于問題的解決,學生的認識也會得到不斷提升。同時,所設計的問題注重了方法的指導,如用給出具體例子的方法來研究規律,選擇性地研究連加的和的奇偶性,突出研究的重點、發現和困惑,把自己的研究發現向爸爸媽媽介紹并尋求他們的幫助,等等。】
三、交流,展示問題解決的過程
1.研究兩個數相加的和的奇偶性
師:小組內交流課前研究的情況,說說你是從哪入手的?
生1:先研究兩個數相加的情況,我是用舉例的方法來研究的。
奇數+偶數:1+2=33+6=95+18=23
奇數+奇數:1+3=43+7=1113+57=70
偶數+偶數:2+4=66+8=1410+20=30
師:兩個數相加的和的奇偶性有怎樣的規律呢?
結論:(1)奇數+偶數=奇數;(2)奇數+奇數=偶數;(3)偶數+偶數=偶數。
師:光有幾個例子好像不夠嚴謹,再舉例子好像又舉不完,你能解釋嗎?
生1:其實很簡單!偶數除以2沒有余數,奇數除以2余數是1。(1)中相除后有余數1,所以和是奇數;(2)中兩次相除都有余數1,相加就是2,也就是說合起來再除以2就沒有余數了,所以和是偶數;(3)就不用解釋了。
師:大家都聽明白了嗎?
【思考:課內的師生互動應高于課前學生的自主學習的收獲,因此新的問題“你能解釋嗎?”不是低層次的重復,而是新的認識。課堂教學的價值,應體現在學生認識的提升上。在展示了學生研究的結論之后,教師提出新的問題“光有幾個例子好像不夠嚴謹,再舉例子好像又舉不完,你能解釋嗎?”讓學生在解釋中認識得到了提升——從感性走向理性,從歸納走向說理。】
2.研究幾個數連加的和的奇偶性
師:研究連加的和的奇偶性,你重點研究的是幾個數相加?采用的是什么方法?(分別請研究3個數、4個數、5個數連加的學生或小組向全班介紹研究結果。匯報的情況顯示,學生研究幾個數連加的和的奇偶性基本上還是采用的舉例法。)
師(在肯定學生方法的基礎上):能不能不舉例子,利用兩個數相加的和的奇偶性的規律,去揭示幾個數連加的和的奇偶性的規律呢?
師:四個數連加有幾種情況?
①奇數+奇數+奇數+奇數;②奇數+奇數+奇數+偶數;③奇數+奇數+偶數+偶數;④奇數+偶數+偶數+偶數;⑤偶數+偶數+偶數+偶數。
生1:⑤偶數+偶數+偶數+偶數=偶數;①奇數+奇數+奇數+奇數=(奇數+奇數)+(奇數+奇數)=偶數+偶數=偶數。
生2:②奇數+奇數+奇數+偶數=奇數+(奇數+奇數)+偶數=奇數+偶數+偶數=奇數+偶數=奇數。
生3:③奇數+奇數+偶數+偶數=偶數+偶數+偶數=偶數。
生4:④奇數+偶數+偶數+偶數=奇數+偶數=奇數。
【思考:學生課前是采用舉例法研究連加的和的奇偶性的。交流后教師用新的問題“能不能不舉例子,利用兩個數相加的和的奇偶性的規律去揭示幾個數連加的和的奇偶性的規律呢?”驅動學生向認識的更深處進發,促進學生充分利用掌握的規律去解釋說明更為復雜的情況。】
3.揭示和的奇偶性
(1)師:連加時和的奇偶性可能跟什么有關?
生1:與前兩個數的和有關。
生2:與加數中奇數的個數有關。
(2)獨立完成下表
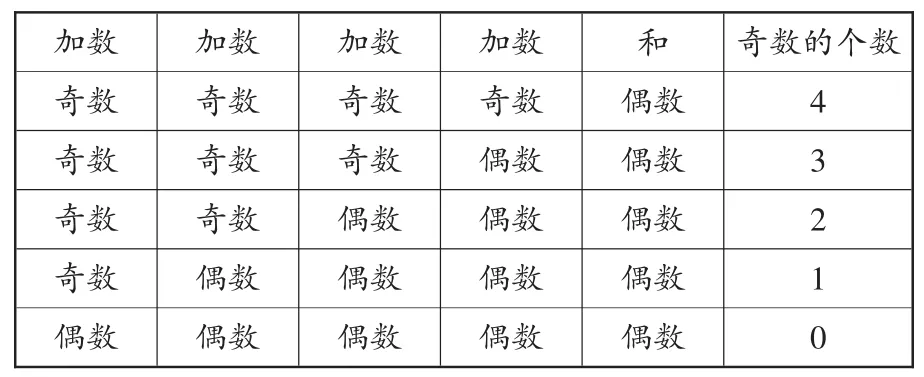
加數 加數 加數 加數 和 奇數的個數奇數 奇數 奇數 奇數 偶數 4奇數 奇數 奇數 偶數 偶數 3奇數 奇數 偶數 偶數 偶數 2奇數 偶數 偶數 偶數 偶數 1偶數 偶數 偶數 偶數 偶數 0
(3)驗證多個數連加的情況后回答之前提出的問題。
(4)結論:幾個數連加,加數中奇數的個數是奇數時,和是奇數;加數中奇數的個數是偶數時,和是偶數。
【思考:在學生分別用舉例法和說理法逐步研究了兩個數相加、幾個數連加的和的奇偶性之后,教師用新的問題“連加時和的奇偶性可能跟什么有關?”將研究推到一個新的高度。通過填表歸納出和的奇偶性的規律,使學生經歷從感性向理性升華的認識過程。】
四、遷移,將問題研究擴展
師:下面每道算式的結果是奇數還是偶數?你有什么發現?
3×5,4×6,3×7×2,3×7×2×6
師:下面的連乘算式的積是奇數還是偶數呢?
3×5×7×9×11×23×35
3×5×7×9×11×23×35×17×4×513
生1:只要因素中有偶數,積就一定是偶數。
師:如此看來,判斷連乘的積的奇偶性,關鍵看什么?
結論:連乘時,因數中只要有偶數,積就一定是偶數;如果因數中沒有偶數,積就是奇數。
【思考:在探索和的奇偶性規律的基礎上,通過幾道具體的乘法計算題,利用“判斷連乘的積的奇偶性,關鍵看什么?”這個問題,使簡約研究的過程直抵結論,體現了問題的力量!】
五、反思,讓研究再次升華
師:和的奇偶性與積的奇偶性有什么異同?
生:和的奇偶性,看加數中奇數的個數,如果有奇數個奇數,那么和就是奇數;如果有偶數個奇數,那么和就是偶數。積的奇偶性,只要看因數中有沒有偶數,只要因數中有偶數,那么積就一定是偶數;如果因數中沒有偶數,積就是奇數。
師:你有新的理由嗎?運用所學知識解釋課前問題導學單上的最后一道題。(略)
【思考:課末的反思性問題,既與課首的問題形成呼應,又是對所學內容的應用,可以促進學生元認知能力的提高。】
好課的基因有若干個,但有一個基因是永遠都存在的——問題設計。勞凱聲教授認為:“問題是介于認識的此岸和彼岸之間的認知對象,如果它完全處于此岸,已被我們解決了,就不稱其為問題;如果它完全處于彼岸,我們完全沒有接觸到、意識到,也就不能稱其為問題。因此,問題應該是介乎認識的此岸和彼岸之間,被我們接觸到、意識到并試圖回答、解釋,或者采取相應行動的這一類認知對象。”鑒于以上的認識,我們可以這樣認為:首先,問題意味著矛盾和不平衡,即在認識的此岸存在著困惑;其次,問題意味著意義和完善性,即在認識的彼岸得到了解決;再次,問題意味著探究和建構性,即從認識的此岸走向彼岸;最后,問題意味著批判和反思性,即發展學生的解決問題思維。因此,教學中,教師應科學設計問題,以激發學生的學習動機,彰顯學生的主體地位;以問題聚焦學習內容,凸顯學習目標;著力問題解決,培養學生的探究能力;圍繞問題展示,促進學生的良性互動;強化反思梳理,發展學生的元認知能力。通過問題驅動,讓學生從認識的此岸走向勝利的彼岸。
(責編金鈴)
[中圖分類號]G623.5
[文獻標識碼]A
[文章編號]1007-9068(2016)05-007

