薄板彎曲加權殘值法的研究

林 松

(中國航天建設集團有限公司第二設計分院，北京 100071)

薄板彎曲加權殘值法的研究

林 松

(中國航天建設集團有限公司第二設計分院，北京 100071)

用加權殘值法對四邊簡支距形薄板及環扇形薄板進行了研究，同時給出算例表明該方法簡單易行、精度高，收斂速度快.

矩形薄板；扇形薄板；加權殘值法

0 引 言

加權殘值法是一種半解析、半數值的方法，我們可以首先設試函數，然后通過控制方程和邊界條件，把難以求解的微分方程問題轉化為容易求解的代數方程.這樣我們可以很容易求解相關工程問題.用這種方法解決固體力學的問題具有簡單、準確、計算工作量少等優點.本文利用該方法對薄板彎曲問題進行了分析和研究.并通過算例與精確解比較，說明該方法簡單易行、精度高、收斂速度快.

1 四邊簡支矩形薄板

薄板撓度與外載滿足下列方程：

DW4(x,y)=q(x,y)

(1)

該矩形薄板，邊長為a，寬為b，則其邊界條件為：

(2)

把均布荷載寫成二維DiracDelta函數

q=pδ(x-ξ)δ(y-η)

薄板彈性曲面微分方程為

DW4(x,y)-pδ(x-ξ)δ(y-η)=0(3)

設薄板撓度函數取為

(4)

應用加權殘值法，得到

(5)

其中

Hi=DW4(x,y)-p(δ-ξ)δ(y-η)

求解方程組(5)，得到

(6)

把系數(6)，代入撓度表達式中得到

(7)

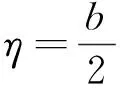
(8)

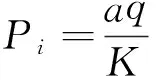
(9)

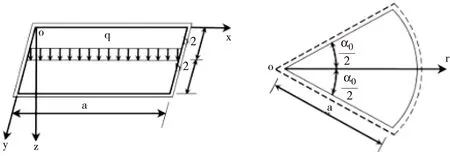
圖2 圖3

2 周邊簡支扇形板

對圖3板面受均載q的簡支扇形薄板，設位移函數為

(10)

其中B0、B1、B2、B3是由邊界條件確定的任意常數，B為待定參數，x=r/a，且有

(11)

將撓度(10)代入以下薄板邊界條件

(W)X=0X=1=0,(MX)X=0X=1=0

解出四個常數

(12)

圓板撓度彈性曲面微分方程是

(13)

將式(10)代入式(13)中，得域內殘值S=S(B,x,θ)，然后應用伽遼金加權殘值法，得

進而求得參數

B=520+106μq0a4α0/C

(14)

并且

其中

把所求……