對CANDU燃料組件結構的一維瞬態輻射程序開發與驗證

高新力，王昆鵬，趙傳奇，蘇光輝

(1. 西安交通大學能源與動力工程學院，陜西西安710049； 2.環境保護部核與輻射安全中心，北京100082)

對CANDU燃料組件結構的一維瞬態輻射程序開發與驗證

高新力1,2，王昆鵬2，趙傳奇2，蘇光輝1

(1. 西安交通大學能源與動力工程學院，陜西西安710049； 2.環境保護部核與輻射安全中心，北京100082)

在氣冷CANDU式燃料組件之中，輻射換熱也是不容忽視的一部分。特別是在出現了系統失壓/失流事故時，輻射換熱將會成為保證燃料安全的主要冷卻手段。本文中針對CANDU式壓力管編制了針對壓力管幾何條件下的一維輻射換熱瞬態程序。程序中采用將燃料元件棒轉化為同心圓環的方式簡化輻射角的計算，并加入了隔層輻射模型，使模型更加貼近實際。采用分別將程序中的幾個模塊的計算結果與CFX計算結果對比的方式來達到程序驗證的目的，驗證結果顯示程序RHTPB具有良好的表現，能夠滿足于反應堆安全計算的需要。

CANDU組件；輻射換熱；瞬態程序

德州大學奧斯汀分校所開發的壓力管式聚變裂變混合堆概念[1]，為了能夠有效地減小冷卻劑的電磁效應和中子慢化效應，并減少腐蝕，采用了氦氣冷卻方案。同時，為了減小中子需要穿透的結構壁的厚度并較好地承受住冷卻劑的壓力，概念中采用了CANDU式的壓力管式組件設計。

對于氣體冷卻反應堆的非能動冷卻系統設計來說，現階段主要采用的是依靠氣體自然循環能力帶走余熱或者采用熱傳導將余熱排出的方案。然而對于壓力管式聚變裂變混合堆的氦氣系統，兩種方案都存在一些困難。首先依靠氣體自然循環能力來帶走反應堆余熱的設計需要保證堆芯的壓降足夠小，這就需要較高的堆芯冷卻劑體積比[2]。同時，因為氣體的自然循環能力較小，為了保證燃料溫度低于限值，就需要提高冷卻劑設計壓力，這就會造成反應堆工程造價的提高。而對于依靠熱傳導和熱輻射來將余熱帶出反應堆的系統，需要反應堆內材料具有較大的導熱系數，且擁有較大的堆芯內的燃料占空比。而對于壓力管式氦氣冷卻混合堆來說，由于處在聚變堆之中，結構受到很大的限制，而氦氣的自然循環能力很差，因此，德州大學奧斯汀分校的設計概念采用了一種新式的余熱排出系統設計方案，使用熱管作為介質，依靠輻射換熱將壓力管內的余熱排出。

在此類余熱排出系統中，熱管參數、壓力管參數和輻射換熱量等關鍵因素都會影響到系統的正常工作。因此，在系統設計過程中，有必要進行CANDU式燃料組件內的輻射換熱計算。現階段，計算程序CHAN-II[3]以及CATHENA[4]已經能夠用于預測表面輻射在熱輻射中作為主要輻射方式時的情況。同時，CFX、Fluent等有限元分析程序也被證明能夠用于計算CANDU式的燃料棒幾何內的輻射換熱工況。但是，這些程序應用起來較為復雜，特別是有限元商業程序計算瞬態工況耗時很長。針對上述問題，為了滿足設計開發的需求，本文開發了一種新的計算程序RHTPB，能夠快速進行CANDU式壓力管內的輻射換熱計算。

1 瞬態輻射程序的開發

1.1 基本假設

在壓力管內輻射換熱計算過程中，為了簡化計算，我們做了一些基本假設：

(1) 參與輻射的物體表面(包括壓力管內壁、燃料包殼外壁)都是漫射(漫發射、漫反射)灰體；

(2) 不考慮壓力管或者燃料元件上的軸向溫度傳遞；

(3) 同一根燃料組件內燃料的功率相同。

1.2 數學模型

由于氦氣為分子結構對稱的雙原子氣體[4]，在工業上常見的溫度范圍內，實際上沒有發射和吸收輻射能的能力，可以認為是熱輻射的透明介質。另外，由于程序計算的對象是氦氣冷卻壓力管式燃料元件發生失流的情況，在此過程中，氣體不存在對流換熱，加上氦氣導熱能力并不是熱傳遞的主要因素。因此，從系統設計角度來說，為了獲得保守的結果，在計算過程中，不考慮氦氣對輻射的吸收以及氣體的導熱和對流，只考慮燃料元件內部的導熱及燃料元件表面間的輻射換熱。

因此，燃料芯塊的瞬態熱傳導方程為：

(1)

對于燃料包殼的瞬態熱傳導方程為：

(2)

邊界條件為：

其中，ρu為燃料芯塊的密度；ρc為燃料包殼的密度；cu，Qv為燃料芯塊體積釋熱率；R代表著包殼的輻射換熱。因此，如何確定燃料元件間輻射換熱量就成了求解燃料元件溫度的關鍵問題。

在復雜系統中，輻射角的計算一直是輻射熱量計算的關鍵問題。對于CANDU式的棒束來說，本身有著中心對稱和圓周均勻的幾何，且在模型中，同一燃料組件內功率近乎相等，因此，燃料棒束的同一環上的燃料元件溫度分布基本相同。基于以上原因，本文采用了一種合理的簡化方式對燃料組件內的輻射換熱進行計算。如圖1中所示，程序中假設燃料組件里的燃料棒能夠被近似轉化成為幾個同心的圓環，輻射換熱只在相鄰的燃料環表面進行傳遞。同時假設燃料元件棒束的軸向無限長。這種假設能夠大大降低CANDU式棒束幾何的輻射角計算難度，但同時這種假設的缺點在于每個燃料元件上表面的周向不同位置的溫度區別不能很好地體現出來。

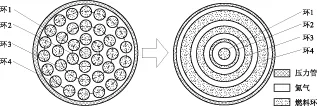
圖1 輻射模型轉變方法Fig.1 Radiation Model Transforming Method

模型轉換的過程中，確定每一環的內外半徑時，需要保證轉換后模型中每一環燃料元件的內外表面積分別等于實際模型中每一環上燃料元件的對內總輻射面積和對外總輻射面積。而對內輻射面積和對外輻射面積由具體的棒束幾何所確定。同時，為了保證每一圈燃料環擁有與之相應的燃料元件相同的功率，模型轉換過程中還根據轉換前/轉換后的面積比調整了功率密度。例如在圖1中，原模型中環2上有6根燃料元件棒，經過轉換后，變成了右側模型中的環2，其中環2的內表面面積與棒束模型中第二圈中所有的燃料棒的能夠向內輻射熱量的表面積相同，外表面積與棒束模型中第二圈中所有的燃料棒的能夠向外輻射熱量的表面積相同。

然而，顯而易見的是這種逐層輻射的模型與實際情況中的輻射熱量傳遞方式有著較大差異。在棒束模型之中，燃料元件不僅僅與相鄰環上的燃料元件進行輻射換熱，并且與隔層的燃料棒進行了輻射換熱。為了保證模型盡可能的貼近真實情況，假設模型中不僅存在相鄰層之間的輻射能量傳遞，同時也有隔層輻射之間的能量傳遞。如圖1中，從環1表面中發出的輻射能量不僅僅被環2的內表面接收，同時還被環3的一部分內表面所接收。這樣的話，計算所用的2面封閉輻射系統變成了圖2中所示的3個面所組成的封閉輻射系統。其中，表面1到表面4的輻射角等于圖1中環3上空隙所占的比例。

圖2 輻射電阻模型Fig.2 Radiation Resistance Model

2 瞬態程序的驗證

因為缺乏實驗數據，程序中的輻射模型、瞬態輻射計算模塊以及穩態輻射計算模塊分別由CFX進行了校核。

2.1 穩態結果校核

本文使用RHTPB程序和CFX對同一穩態算例進行計算，并通過與算術解進行對比來驗證程序中穩態輻射計算的正確性。

穩態算例是對幾個同心圓環中的輻射換熱量進行計算。如圖3中所示，最內環的固態輻射盤的半徑為R1,out，其余各個同心圓環的內外半徑由內至外依次為R2,in,R2,out,R3,in,…R5,in。所有表面的發射率假設為0.8。假設環間氣體為氦氣。氦氣作為雙原子對稱結構，可以視作輻射透明介質，因此燃料環表面之間的熱傳遞僅僅通過熱輻射進行。兩個相鄰的表面間，比如環2的外表面與環3的內表面，組成一個完整的封閉輻射系統。假設燃料元件和壓力管的材料導熱率都足夠大，使每個環內部的溫度差小到足以忽略。每一個燃料環內的功率密度均為0.8MW/m3，并假設壓力管的外表面的溫度為573K恒溫。

圖3 穩態驗證算例Fig.3 Steady State Verification Example

使用CFX進行計算時，假設材料的導熱率為5000 W/(m2·K)，使每個環內部的溫度差小到足夠忽略。模型兩端設置為對稱邊界條件，以保證可以等效為無限長的圓柱體。由于采用He作為氣體工質，將氣體導熱系數設置為0，同時將氦氣的輻射吸收系數設置為0，并采用適合計算無氣體輻射的Monte Carlo模型來模擬氦氣輻射透明的特性。經過對不同網格數量的CFX模型進行了敏感性分析后選擇了合適數量的網格，如圖4給出了CFX計算的網格。

圖4 穩態驗證算例網格Fig.4 Mesh of Steady State Verification Example

圖5中給出了CFX計算結果的溫度分布圖。圖中可以看出，由于材料的導熱率設置的足夠大，每一環的溫度均一致。溫度從內向外逐層降低，最外層的溫度為573K，而最內側的燃料棒溫度為887K。

圖5 穩態驗證算例的CFX計算結果Fig.5 Steady state result of CFX calculation

表1中給出了穩態算例的結果對比，從表中我們可以清晰看出程序RHTPB的計算結果和數值解保持了非常好的一致性，證明程序RHTPB在輻射換熱量計算上的合理性。同時，CFX計算結果與數值結果相差很小，可以認為CFX用于輻射性計算具有相當的可靠性，且計算中模型設置方法正確，可以作為程序校核的參考。

表1 CFX穩態算例計算結果與RHTPB

2.2 模型校核

為了檢測RHTPB程序中將CANDU式燃料組件處理成幾個同心圓環來計算輻射換熱的方法的正確性，本文將RHTPB計算結果和CFX計算結果進行比較。另外，由于幾何結構復雜，輻射角難以計算，難以計算出數值解。因此，我們采用對幾何結構不敏感的CFX進行對比計算，來驗證RHTPB程序的計算結果。

圖6給出了計算對象的截面圖。如圖中所示，壓力管內共有37根燃料元件。按CANDU式燃料組件方式排列，37根燃料元件分別處在4個不同半徑的同心圓上。燃料為壓水堆式燃料棒，內部為UO2芯塊，外部包裹著燃料包殼，包殼與燃料棒間的等效熱傳導系數為5678 W/(m2·℃)。燃料元件在兩端固定，因此內部無其他定位格架影響棒間輻射。燃料元件長度遠大于10倍直徑，可等同無限長圓柱間傳熱問題。氦氣為雙原子對稱結構，對于熱輻射的吸收能力非常小，可視作輻射透明介質。

圖6 模型轉化方法驗證算例Fig.6 Modeling Method Verification Example

CFX計算中，選擇Monte Carlo輻射模型模擬壓力管內的氣體透明輻射特性。燃料棒的功率密度為0.8MW/m3，壓力管的外表面的溫度為573.1K恒溫，燃料棒的初始溫度設置為625K。包殼與燃料棒間的等效熱傳導系數為5678 W/(m2·℃)。壓力管兩端為對稱邊界，從而能夠消除壓力管長度對輻射角的影響。所有輻射表面的發射率假設為0.8。

圖7給出了CFX計算的計算網格。網格采用六面體網格劃分，質量達到0.5以上，并經過網格數量敏感性測試，保證了計算結果的網格無關性。圖8給出了壓力管輻射問題的CFX計算結果。可以看出，由于燃料元件內部的功率較低，燃料元件內的功率分布較為均勻。燃料元件的溫度由內至外依次降低，且由于幾何結構的中心對稱性，同一環上的壓力管溫度相同。

圖7 模型轉化方法驗證算例的計算網格Fig.7 Mesh for Modeling Method Verification Example

圖8 模型轉化方法驗證算例的CFX計算結果Fig.8 CFX Result for Modeling Method Verification Example

在RHTPB程序的計算過程中，會將圖7中的燃料組件模型轉化為圖9中所示的同心圓環燃料形式，圖9中還給出了轉換后模型的具體尺寸。其尺寸確定原則為：每一環的內/外表面積分別等于圖7中燃料組件模型上相應環上的燃料棒的向內/外輻射面積。例如圖9中的表面7，其表面積等于壓力組件中第4環上18根燃料組件的能夠直接與壓力管進行輻射換熱的表面積之和。但這也導致每一環的燃料環體積與燃料組件內相應的燃料棒體積不同，程序內通過改變燃料環內的功率密度使得轉化后的模型與原模型擁有相同的總功率。另外，燃料環厚度的變化，也會影響到燃料元件內部導熱的計算，因此在燃料棒內導熱計算過程中，燃料環的厚度不作為導熱計算的輸入，而是使用燃料棒的直徑作為燃料環導熱的傳輸距離，使設計結果更為保守。

圖9 程序RHTPB模型轉化結果Fig.9 Modeling Transfer Result of RHTPB

可以看到在實際的燃料組件模型中，燃料元件不僅僅和相鄰環上的燃料元件進行換熱，同時還會穿過燃料元件之間的縫隙與間隔層進行輻射換熱。因此，為了使轉化后的模型更加接近真實模型，我們假設在轉化后的模型中，輻射不僅僅存在于兩個相鄰的表面間，也存在于相隔的燃料元件環之間。比如輻射換熱不僅僅存在于表面1與表面2之間，在表面1與表面4之間也存在輻射換熱。

圖10給出了CFX與程序RHTPB的計算結果對比。為了體現出間隔輻射模型對計算結果的影響，程序RHTPB分別對采用間隔輻射模型和不采用間隔輻射模型的情況進行了計算。圖中可以看出，不采用間隔輻射模型時，程序RHTPB計算出的每層燃料環的最高溫度遠遠高于CFX計算出的每環燃料的最高溫度。而采用間隔輻射模型時，程序RHTPB計算結果與CFX計算結果相對符合較好，且程序計算結果溫度比CFX的計算結果高，滿足設計中保守計算的需求。另外，不考慮間隔層燃料環之間的輻射時，每層燃料環之間的溫差也更大。而在考慮了間隔輻射之后，每層燃料環之間的溫度變化也相對平緩，更貼近CFX計算出的結果，說明間隔輻射模型更符合實際情況。

圖10 間隔輻射模型計算結果對比Fig.10 Comparison of Result calculated with and without gap radiation model

2.3 瞬態工況驗證

為了驗證程序的瞬態計算模塊是否正確，本文使用RHTPB和CFX對同一瞬態算例進行計算，并將結果進行比較。

如圖11所示，瞬態工況包含從一個自發熱的內管向外側的薄管輻射換熱的瞬態過程，假設里側的發熱盤和外側的薄管的熱導率非常大從而能夠保證其內部的溫差小到可以忽略。輻射表面發射率均為0.7，表面2恒定溫度873.15K。假設表面1和表面2之間只有輻射換熱。在T0時刻，內管突然停止發熱，計算之后內管溫度的變化情況。

圖11 瞬態工況驗證算例Fig.11 Transient State Verification Example

圖12中給出了CFX和程序RHTPB計算結果比較。圖中黑點為H.T.KIM用CFX計算的結果[6]。代表程序RHTPB計算所得到的結果。可以看出，內部的管壁溫度T1從初始溫度1673.15K開始下降，直至最終降至與外側溫度T2相同。由于輻射換熱量隨著溫差減小而減小，溫度下降的速率也越來越慢。程序與CFX計算結果符合非常好，證明了程序瞬態計算模塊的可靠性。

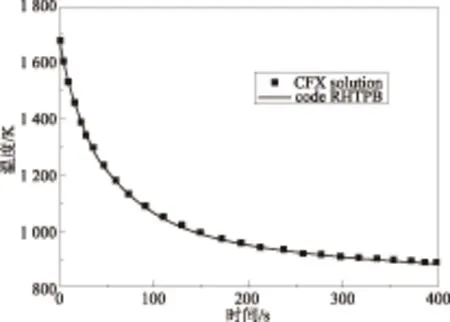
圖12 瞬態工況驗證結果Fig.12 Comparison of CFX and RHTPB Result for Transient State Verification Example

3 總結

本文提出了一種計算CANDU式燃料組件內輻射熱量計算的簡化方法，并編制了程序RHTPB。通過加入間隔輻射模型，減小了環形燃料輻射模型與實際輻射模型的計算結果的差距。本文通過分別校核程序中的輻射模型、

瞬態輻射計算模塊以及穩態輻射計算模塊來達到驗證校核程序的目的。與CFX結果的比較證明了程序計算結果的可靠性，證明了本程序可以應用于氦氣冷卻的CANDU壓力管式反應堆失流事故后燃料棒溫度計算。

后續工作將圍繞加入非輻射透明氣體模型展開，研究非輻射透明氣體介質對輻射換熱的影響。

[1] M Kotschenreuther, P M Valanju, S M Mahajan, E A Schneider. Fusion-Fission Transmutation Scheme—Efficient destruction of nuclear waste[J]. Fusion Engineering and Design， 2009，84(1) ：83-88.

[2] M A Pope，J I Lee, P Hejzlar, M J Driscoll. Thermal hydraulic challenges of Gas Cooled Fast Reactors with passive safety features[J] . Nuclear Engineering and Design，2009，239(6)：840-854.

[3] D Bowslaugh. CHAN-IIA MOD 2.0: Prediction of CANDU Fuel Channel Behaviour Under Prolonged Low Flows—Program Description[J]. Atomic Energy of Canada Limited，1993, vol.TTR-490.

[4] B N Hanna. CATHENA: A thermal hydraulic code for CANDU analysis[J].Nuclear Engineering and Design，1998，180(2)：113-131.

[5] 楊世銘,陶文銓.傳熱學[M].北京:高等教育出版社，2006：419-420.

[6] H T Kim, B W Rhee, J H Park. “Benchmark calculations of a radiation heat transfer for a CANDU fuel channel analysis using the CFD code[J]. Journal of Nuclear Science and Technology，2006，43(11)：1422-1430.

Development and Verification of a One Dimensional Transient Radiation Code for CANDU Fuel Assembly

GAO Xin-li1，2，WANG Kun-peng2，ZHAO Chuan-qi2，SU Guang-hui1

(1. School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2.Nuclear and Radiation Safety Center, Ministry of Environmental Protection, Beijing 100082, China)

In the Gas-cooled CANDU kind fuel assemble, radiation heat transfer cannot be ignore. Expertly during the LOFA accidents, with no convection heat transfer, the radiation heat transfer will become the main force to ensure the safety of the reactor. This paper developed a one dimensional transient radiation code to calculate the radiation heat transfer in CANDU fuel assembly. The code assumes that the fuel element rings can be lumped into several circular rings, which can simplify the calculation of radiation angle factors. And with the purpose of making the models closer to the actual situation, radiation between next nearest neighbor layers is also considered in addition to that between nearest neighbor layers. The radiation model, transient radiation calculation and steady radiation calculation of the code RHTPB are verified by comparing with result of CFX, respectively. The result shows that the code has good performance in transient radiation calculation, and can satisfies the need of nuclear industry.Key words: CANDU Bundles; Radiation Heat Transfer; Transient Code

2016-02-11

高新力(1988—)，男，陜西省，工程師，博士，核科學與技術專業，現從事核安全科研方向工作

TL333

A

0258-0918(2016)06-0739-07