多級離心泵多工況壓力脈動數值模擬

黃 茜，袁壽其，方玉建，張金鳳，張 霞(江蘇大學流體機械工程技術研究中心，江蘇 鎮江 212013)

多級離心泵以較高揚程特點廣泛應用于水利、石油輸送，農業灌溉，工廠給水，工業生產等領域[1]，其結構較為復雜和緊湊，水力設計的限制因素也較多，提高離心泵整機運行性能難度較大，故有必要深入開展離心泵內部流動模擬，進一步揭示流動機理，探求多級離心泵運行過程中的振動特性及其對泵性能的影響。一些學者紛紛展開了相關研究，發現實際運行過程中會出現強烈的噪聲和振動[2,3]。引起泵振動的主要原因：當泵的轉動頻率接近泵部件的固有頻率時所產生的共振；機械加工、裝配、安裝不當引起的振動等[4-6]；由于內部非定常流動等因素引起流體壓力脈動引起的振動。其中，由于水力因素誘發的振動較為復雜[7-12]。有研究發現：多級泵內部葉輪與導葉之間存在動靜干涉，且該干涉作用可能由于共振而增強[13]，流動導致的振動直接體現在流場內的非定常壓力脈動，而振動也會加劇泵部件的磨損，嚴重時造成泵運行的失穩[14]。因此從流動和壓力脈動的角度對多級泵的振動性能和穩定運行進行研究。

目前，國內外很多學者對離心泵內部流場壓力脈動現象進行了研究。Guo等[15]和Arbdt等[16]對導葉式擴壓器離心泵的壓力脈動和振動進行了試驗研究，發現壓力脈動的周向不均勻性，脈動幅值在葉輪出口處最大。Benra等[17]通過數值模擬的方法研究了旋轉葉片和靜止部件相互干擾造成的壓力脈動。司喬瑞等[18]分析了不同時刻葉片與隔舌相對位置對模型泵瞬時性能及壓力脈動的影響，并利用數理統計學原理和時-頻域數據處理方法對流場內監測點的壓力脈動進行分析。裴吉[19]等研究表明不同運行流量對泵內周期性壓力脈動的強度和位置有明顯作用。

在這些研究的基礎上，本文以某5級離心泵為研究對象，建立包含葉輪、徑向導葉、前后泵腔、口環間隙以及進出口管道的流場模型。應用ANSYS-CFX軟件進行非定常數值模擬[20]，重點對葉輪和徑向導葉交界面內的壓力脈動進行了研究，分析各監測位置點的壓力脈動特性，以期為改善多級離心泵的流動誘導振動，提高泵的使用穩定性提供一定的理論依據。

1 計算模型

1.1 水泵參數

農業灌排用臥式5級離心泵的主要性能參數分別為：設計流量Q=10 m3/h，單級揚程H=8 m，轉速n=2 800 r/min。葉輪主要水力尺寸：D2=103 mm、出口寬度b2=10 mm、葉片數Z=6；導葉主要水力尺寸：基圓D3=105 mm、外徑D4=118 mm、葉片數為12。與其他導葉相比，徑向式導葉的正反導葉間通流更為順暢，產生的水力損失較小。

1.2 計算域和網格劃分

從葉輪出口的邊界條件和級間相互作用來看，多級離心泵的復雜程度遠高于一般的蝸殼式單級離心泵，文中選取2級葉輪和導葉的流域進行數值模擬，重點研究次級葉輪和導葉交界面和次級葉輪流道內的流動特征。采用ICEM軟件對計算域進行高質量的六面體結構網格劃分，以確保網格質量；將模型的進出口部分作適當延長以獲得較為穩定的數值計算結果；為降低網格數對計算結果準確性的影響，以外特性試驗值作為指標，開展網格無關性驗證；考慮到計算機的配置與計算時間，最終確定網格單元總數為3 421 284，計算域網格如圖1所示。

圖1 計算域結構化網格劃分Fig.1 Computational domain and structured mesh

1.3 計算方法

采用ANSYS CFX 軟件，首先對全流場進行穩態數值計算，計算過程中為了封閉控制方程選取SSTk-ω湍流模型，該模型考慮了湍流剪切應力的傳輸，從而不會對渦流黏度造成過度預測，能精確地預測流動的開始和負壓梯度下的流動分離量。在相同條件下，將穩態數值計算的結果作為非穩態計算的初始值，計算得到整泵內的非穩定流動特性。非定常計算采用Transient rotor 模型模擬葉輪的旋轉，葉輪區域采用旋轉坐標系，導葉、前后泵腔以及口環間隙采用靜止坐標系。進口采用總壓進口邊界條件，壓力值設為1個標準大氣壓，參考壓力設為0，出口采用質量流量出口邊界條件，壁面采用無滑移邊界條件，進口段與葉輪、葉輪與泵腔的Interface設定為Frozen rotor。選取非穩態計算的時間步長為1.785 71×10-4s，即葉輪每旋轉3°為1個時間步長，總時間設為0.106 25 s，即葉輪旋轉8圈，設定收斂殘差標準為10-5。

1.4 監測點位置

由于多級泵的首級葉輪接近于無旋流動，其后各級葉輪進口均為有旋流動，所以對該多級泵的次級葉輪內流場進行壓力脈動進行研究具有一定的代表性。該泵葉輪含6個葉片，且沿圓周方向均勻分布，呈軸對稱形，因此可選次級葉輪中某一流道靠近與導葉交界面處作為研究對象，分別在葉輪內0.9倍出口處和出口處沿吸力面到壓力面的圓周方向取4個監測點，監測點的位置如圖2(a)所示。該模型配合導葉葉片數為12，且正反導葉分布規律一致，均呈軸對稱分布，故同樣分別取某一流道進行研究，正導葉監測點如圖2(b)所示，反導葉監測點如圖2(c)所示。

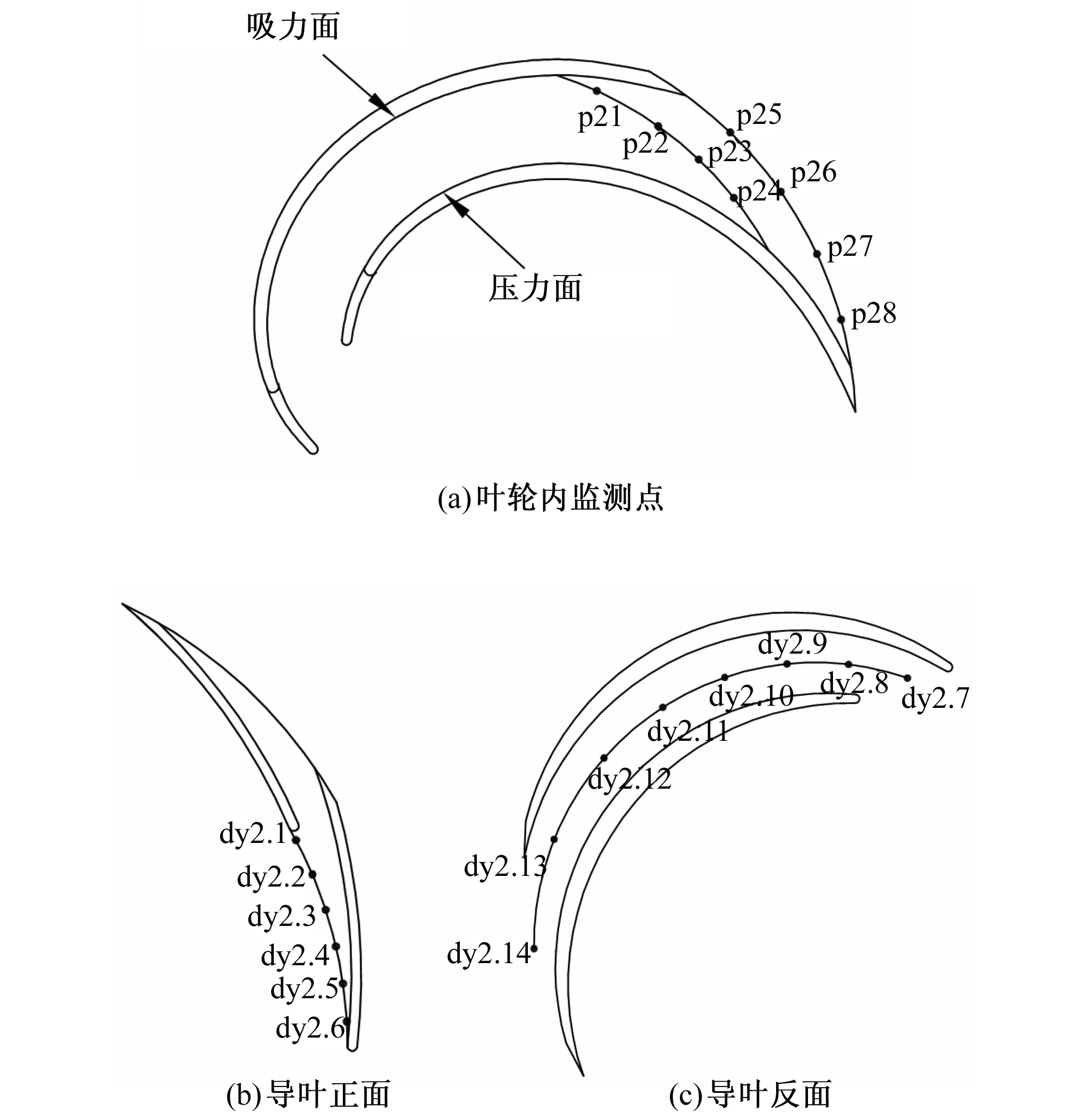
圖2 葉輪和徑向導葉壓力監測點Fig.2 Monitor points at impeller and radial guide vane

2 非定常計算結果與試驗

為了驗證數值計算結果的準確性，對該多級泵做性能試驗，采用精密制造的樣機，在江蘇大學國家水泵及系統工程技術研究中心搭建水泵性能開式試驗臺。

周玲等[21]對多級泵選擇不同的級數進行了數值計算研究，發現不同級數時獲得的多級泵首級效率、揚程相差不大，當級數大于2時，單級揚程的波動隨著級數的增大而減弱，同時次級的揚程與其后各級的揚程基本一致，所以本文將試驗數據與數值計算得到的次級揚程結果進行了對比，結果如圖3所示。

圖3 次級揚程的數值模擬與試驗結果Fig.3 Numerical simulation and experiment of second stage impeller

由圖3可見，在額定流量點及其附近，數值計算結果和試驗結果吻合較好，整體趨勢一致，數值模擬得到的單級揚程比試驗值高3%左右，這主要是數值模擬未考慮機械損失以及實際邊界條件有所不同導致，在偏大流量和小流量區域，誤差也僅在5%左右。整體來看，數值模擬結果可以準確地預測該多級泵的外特性，因此得到數值計算方法是可信的。

2.1 葉輪出口與導葉內壓力脈動

經非定常計算得到各監測點的靜壓，為了比較壓力脈動的大小，現定義壓力系數為：

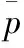
本文中葉輪轉速n=2 800 r/min，則泵軸轉動頻率為46.7 Hz，葉片通過正導葉的頻率(葉頻)為280 Hz。從非定常計算中獲得的瞬態條件下各監測點的靜壓，經快速傅里葉變換，得到相應監測點壓力脈動的頻域分布。

圖4為次級葉輪0.9倍出口和出口處各監測點的壓力脈動特性。可以看出，葉輪出口附近的壓力均隨時間呈現出一定的周期性波動。由于監測點隨葉輪一起旋轉，監測點空間位置不同，所以各壓力波形存在一定相位差。從幅值來看，0.9倍出口處的壓力波動幅值達到出口處的一半，從吸力面到壓力面波動幅值顯著增強。從波形來看，葉輪出口處較為復雜，各監測點的脈動均略顯紊亂，在一個周期內，達到波峰/波谷的數量為12，與導葉數一致。從圖4(c)可以看出，從吸力面到壓力面，壓力脈動規律逐漸清晰。葉輪出口處各監測點的壓力脈動主頻為560 Hz，為2倍的葉頻，正好是導葉葉片數與葉輪葉片數的倍數。

圖4 次級葉輪出口附近壓力脈動特性Fig.4 Pressure fluctuation characteristics at second stage impeller outlet

圖5為正導葉各監測點壓力脈動特性，其中圖5(a)為正導葉各監測點的時域特性。從波形來看，正導葉進口處壓力波動較為紊亂，相差也最為明顯，監測點dy2.1的波動最強烈，幅值近似于葉輪出口處的脈動幅值，正導葉進口邊沿著順時針方向(葉輪沿逆時針旋轉)波動削弱。在一個周期內，達到波峰/波谷的數量為6，與葉輪葉片數一致。圖5(b)為正導葉各監測點的頻域特性，可以看出，各點的壓力脈動主頻為560 Hz,約為2倍葉頻，且在一倍葉頻處伴隨著次主頻。此外，各監測點在高頻出伴有明顯的脈動，從脈動頻率來看，正導葉進口處沿圓周方向的脈動規律是存在差異的。

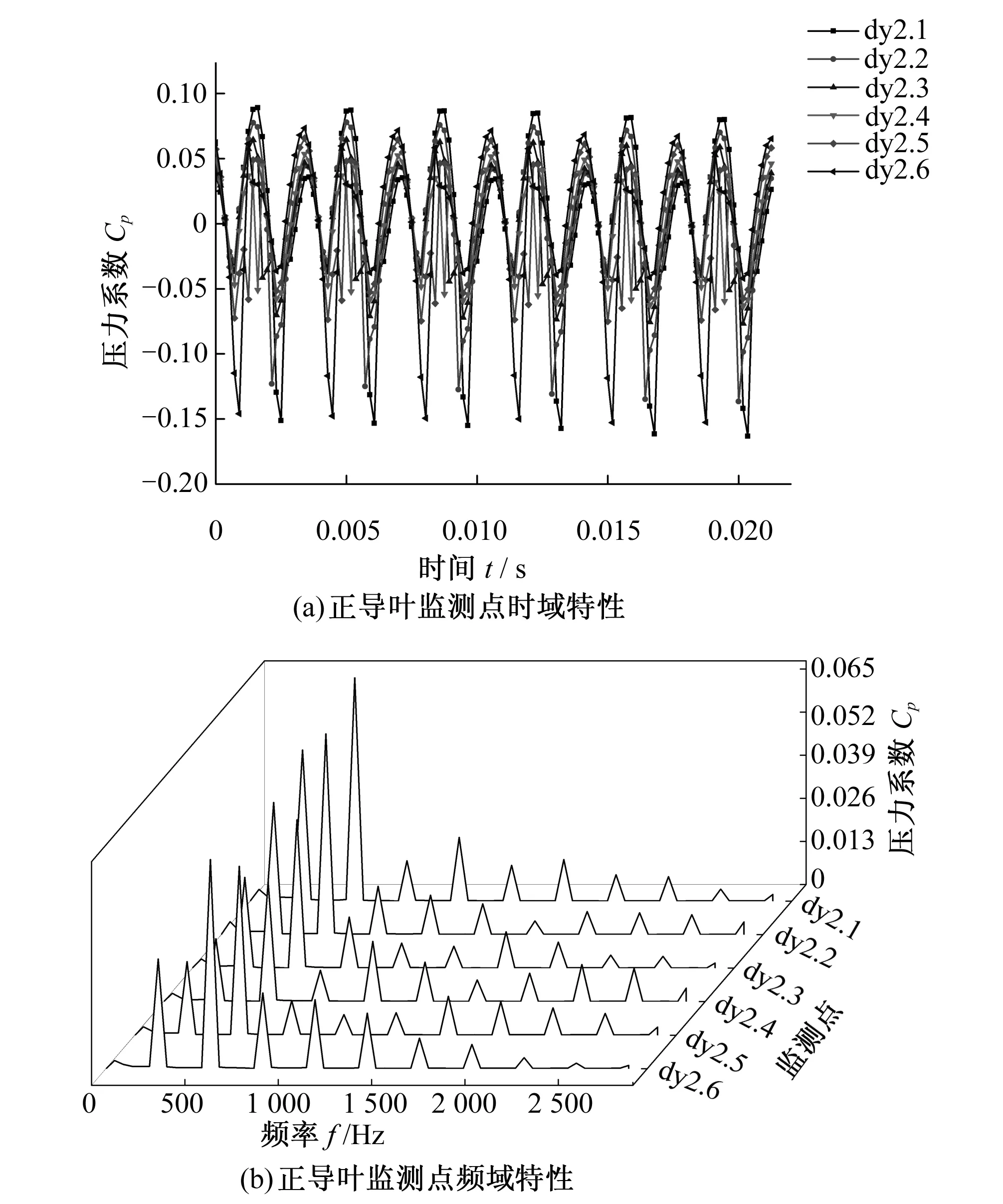
圖5 正導葉監測點壓力脈動特性Fig.5 Pressure fluctuation characteristics at obverse side of guide vane

圖6為反導葉各監測點壓力脈動特性，其脈動波形和幅值近乎相同，脈動主頻仍在2倍葉頻，且壓力脈動強度明顯小于正導葉監測點。此外，可以看出，隨流體流動方向，點dy2.14到點dy2.7壓力脈動的次主頻(1倍葉頻處)逐漸消失，且其他高頻脈動持續減弱，這說明反導葉內流動較為規律，這為流體進入到下一級葉輪起到了很好的引導作用。

圖6 反導葉監測點時域特性Fig.6 Pressure fluctuation characteristics at reverse side of guide vane

綜合對比葉輪出口與導葉內各監測點的壓力脈動，可知葉輪與導葉交界面的壓力脈動強度最大，導葉內壓力脈動受葉輪的影響，離葉輪出口越遠，壓力脈動幅值越小，但最大壓力脈動幅值對應的特征頻率仍為葉頻的2倍，本文認為這與導葉葉片數恰好是葉輪葉片數2倍有關。正導葉內的脈動規律最為紊亂，且在高頻脈動幅值均較大。流體經螺旋段、擴散段進入到反導葉的過程中，壓力脈動幅值逐漸下降，流動區域穩定。

2.2 不同工況下的壓力脈動特性

通過對4個不同工況(0.9Q、1.0Q、1.1Q、1.2Q)下分別從葉輪出口、正導葉進口、反導葉出口中選取3個具有代表性的監測點(p26、dy2.3、dy2.8)進行壓力脈動對比分析，可見，隨著流量的減小，各監測點的壓力脈動顯著增強，如圖7所示。

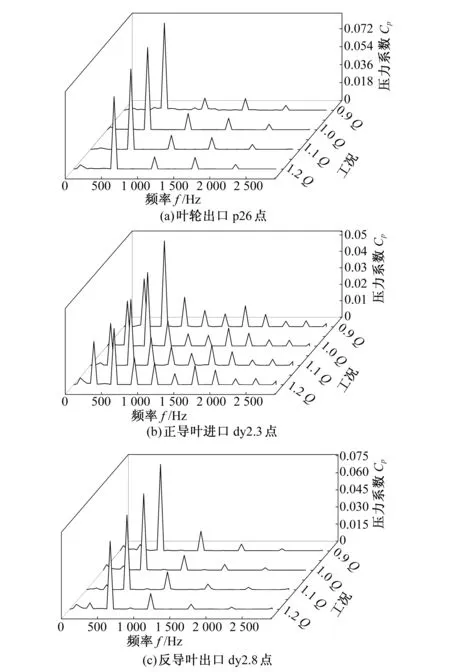
圖7 不同流量下監測點的壓力脈動頻域特性Fig.7 Pressure fluctuation in frequency domain at monitoring points at different flow rates

2.3 振動試驗驗證

由于該模型泵較小，做壓力脈動試驗難度較大，成本也較高。而眾所周知，多級泵內部葉輪與導葉之間存在動靜干涉，并隨共振而增強，流場內的非定常壓力脈動可直接引發振動，這也是振動的主要誘導因素之一，所以從振動試驗的角度來驗證模擬的準確性是有一定參考價值的。在江蘇大學流體中心測試實驗室使用本特利振動儀對該模型泵進行振動試驗，結果如圖8所示，峰值556.25 Hz，為2倍葉頻，且振動幅值較大，說明動靜干涉現象較強烈，同時這也表明了本研究使用的模擬方法正確，結果可信。

圖8 振動試驗數據Fig.8 Vibration test data

3 結 語

(1)多級泵內動靜干涉較為明顯，壓力脈動周期性突出，當導葉數是葉輪葉片數兩倍時，脈動主頻以兩倍葉頻為主。導葉內次主頻為一倍葉頻，并且伴有部分高頻脈動。

(2)在葉輪與導葉交界面的壓力脈動最為強烈，反導葉出口處流動不穩定效應顯得較弱。

(3)隨著流量的減少，泵內各部分壓力脈動幅值顯著增大，偏小流量時對葉輪與導葉交界面的壓力脈動有較大影響。

(4)在多級泵水力優化設計過程中，可基于該研究所提出的非穩態數值模擬方法對導葉和葉片數的組合關系，從動靜干涉引起的壓力脈動幅值和頻率的角度展開評估和優化設計，從而開發出不僅水力性能優良而且具有良好動態特性的多級泵水力模型。

□

[1] 關醒凡. 現代泵理論與設計[M]. 北京：中國宇航出版社，1995.

[2] 徐朝暉. 高速離心泵內全流道三維流動及其流體誘發壓力脈動研究[D]. 北京：清華大學,2004.

[3] 叢國輝,王福軍. 雙吸離心泵隔舌區壓力脈動特性分析[J]. 農業機械學報,2008,(6):60-63,67.

[4] 施衛東,張 磊,陳 斌,等. 離心泵間隙對壓力脈動及徑向力的影響[J]. 排灌機械工程學報,2012,(3):260-264.

[5] 祝 磊,袁壽其,袁建平,等. 不同徑向間隙對離心泵動靜干涉作用影響的數值模擬[J]. 農業機械學報,2011,(5):49-55.

[6] 王 洋,代 翠. 離心泵內部不穩定流場壓力脈動特性分析[J]. 農業機械學報,2010,(3):91-95.

[7] Pavesi G, Cavazzini G, Ardizzon G. Time-frequency characterization of the unsteady phenomena in a centrifugal pump[J]. International Journal of Heat and Fluid Flow, 2008,29(5):1 527-1 540.

[8] 劉厚林,任 蕓,談明高,等. 雙流道泵內壓力脈動的CFD計算及測試[J]. 排灌機械工程學報,2010,(4):277-281.

[9] 朱榮生,蘇保穩,楊愛玲,等. 離心泵壓力脈動特性分析[J]. 農業機械學報,2010,(11):43-47.

[10] 袁壽其,薛 菲,袁建平,等. 離心泵壓力脈動對流動噪聲影響的試驗研究[J]. 排灌機械,2009,(5):287-290.

[11] 袁壽其,周建佳,袁建平,等. 帶小葉片螺旋離心泵壓力脈動特性分析[J]. 農業機械學報,2012,(3):83-87,92.

[12] 靳栓寶,王永生,常書平,等. 混流泵內流場壓力脈動特性研究[J]. 農業機械學報,2013,(3):64-68.

[13] Jiang Y Y, Yoshimura S, Imai R, et al. Quantitative evaluation of flow-induced structural vibration and noise in turbo-machinery by full-scale weakly coupled simulation[J]. Journal of Fluids and Structures, 2007,23:531-544.

[14] Jose G, Carlos. Unsteady flow structure and global variables in centrifugal pump[J]. Journal of Fluids Engineering,2006,128(9):937-946.

[15] Guo Shijie, Maruta Y. Experimental investigations on pressure fluctuations and vibration of the impeller in a centrifugal pump with vaned diffusers[J]. JSME International Journal Series B, 2005,48(1):136-143.

[16] Arndt N, Acosta A J, Brennen C E, et al. Experimental investigation of rotor-stator interaction in a centrifugal pump with several vaned diffu-sers[J]. ASME Journal of Turbomachinery,1990,112(1):98-108.

[17] Berna K F, Dohmen J H. Numerical and experimental investigation on the flow in a centrifugal pump stage[C]∥Proc. WSEAS Int. Conference on Fluid Mechanics, 2008:71-76.

[18] 司喬瑞,袁壽其,袁建平,等. 葉片與隔舌干涉對離心泵性能和壓力脈動影響的數值研究[J]. 流體機械,2012,(8):22-26.

[19] 裴 吉,袁壽其,袁建平，等. 單葉片離心泵壓力脈動強度多工況對比研究[J]. 華中科技大學學報(自然科學版), 2013,(12):29-33,53.

[20] 張永學,李振林. 流體機械內部流動數值模擬方法綜述[J]. 流體機械,2006,(7):34-38,14.

[21] 周 嶺,施衛東,陸偉剛,等. 深井離心泵數值模擬與試驗[J]. 農業機械學報,2011,(3):69-73.