后方交會測量精度影響岡素研究

付海珊

摘 要 交會測量是控制點加密的常用方法，由未知點向控制點觀測進而得出未知點坐標的后方交會法，其應用非常的廣泛，所以對其精度的研究應更加得到關注，本文從角度，邊長，邊角同測的后方交會的近似精度評定公式和考慮起算的數據存在誤差時的嚴密精度評定式出發，分別討論三種不同的后方交會的精度影響因素，并關注這些因素的變化從而導致待定點精度的變化。最后通過實驗實例，分別對邊長，角度，邊角同測等后方交會的精度及坐標進行分析與比較。

關鍵詞 后方交會；測量平差；精度分析

中圖分類號 S29

文獻標識碼 A

文章編號 1674-6708（2016） 154-0049-03

在測量中常常遇到控制點因建筑物阻擋等其他原因造成不能通視，不得不臨時增設測量點來進行測量或工程施工放樣。加設控制點方法有許多，一種較好的方法是在視野遼闊、通式條件好且不容易受到毀損的未知點上用全站儀向已知點進行觀測的后方交會，經研究發現，角度、距離、控制點個數的變化對其精度有很大的影響，本文通過對常用后方交會的原理及精度評定出發，通過數學演算得出這些影響因素是如何影響其精度的，然后在野外進行試驗從而驗證這些規律，本文最后結合工程實例，通過后方交會解算的精度影響因素研究，從而提高未知點精度，進而提高工程質量。

1 后方交會

1.1 定義

定義1（測角后方交會）：后方交會是指僅在未知點P上架設儀器，向最低三個或三個以上的已知控制點4、B、C觀測兩個水平夾角a，B，從而計算未知點的坐標。

由于測距儀以及全站儀逐漸的廣泛使用，后方交會還有如下的兩種解釋：邊長角度同測的后方交會以及僅僅測邊后方交會。

定義2（測邊后方交會）：在未知點P上向控制點，觀測兩個水平距離PA、PB的邊長以、6，再利用三邊求解三角形，從而加密P點的坐標。

定義3（邊角同測后方交會）：在未知的控制點上P上安置儀器，再向已知點A、β觀測兩個邊長的距離以及水平角y，進而求得P點的坐標。

1.2 計算原理

后方交會計算的方法種類有很多，不同種類的后方交會的計算方法也盡不相同。

1.2.1 測角后方交會

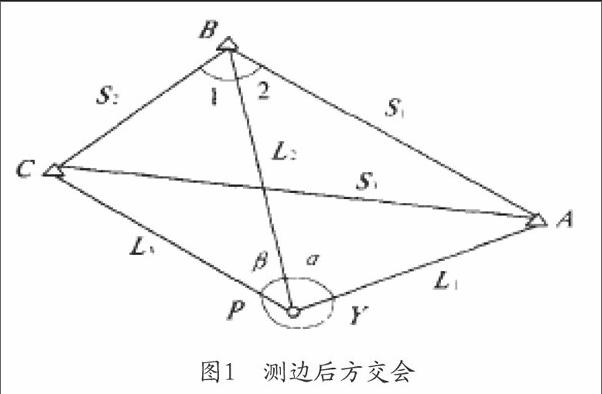
如下圖的圖l表示，已知A、B、C三點的坐標分別為A（Xa，Ya）、B（Xa，Ya）、c（x，，y），觀測角度分別為a，β，再求待定點P的坐標（Xa，Ya）。

1.2.2邊角后方交會

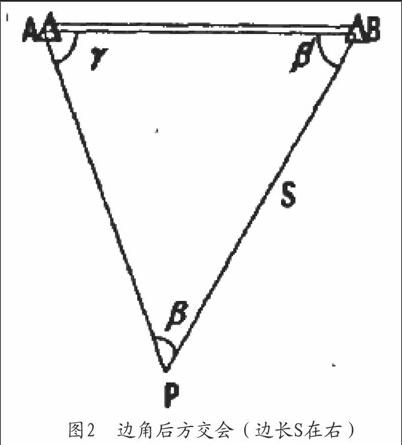
隨著全站儀的全面普及，邊角同測在測量中用的越來越廣泛，其計算可分為以下兩種情況，第一種情況如圖2，A、β位已知點，所以A點與B點的距離SAB以及方位角aBA為已知。觀測量為PB的邊長S以及LAPB的角度B。顯然在這樣的圖形中觀測邊位于觀測角的右邊。

1.2.3測邊后方交會

仍在圖1中，S、s：、S3為三角形的已知邊長，厶1、厶2、厶3為測量的邊長，厶1、厶2為輔助角，求待定點的坐標P （xp，yp）。從理論上來說，只需要兩點的后方距離交會就可計算未知點P的坐標，當有3個已知點或更多點存在時候，則存在一個或對個多余觀測。

2 精度影響因素的研究

2.1 角度后方交會的影響因素

在角度后方交會中（或三點后方交會），如圖1。其P點的X、Y方向的坐標精度，即不考慮初始數據誤差的影響，故P點的坐標中誤差為：

故P點的坐標的精度就可用參數K1、K2、K3來顯現。由于K1、K2、K3是通過觀測的角度變化而變化的，且K1、K2、K3可有引數查表，所以m，的值與交會點P相對于已知點的位置（圖形位置）有關，且與觀測角度的位置有關。

2.2 邊長后方交會的影響因素

在前面的計算與精度評定中，已推算出P點的X、y方向的精度表達式，所以P點的點位中誤差為：

現在考慮全站儀的標稱誤差，即：m2s a2+（6*s）2，式子中，a為固定誤差；b為比例誤差，以毫米（ mm）為單位；S為測距的邊長值，以千米（km）為單位。

正常情況下，在工程測量中，所測的邊長大多在lkm到2km之內，所以當交會點點位分布適宜，所測的兩條邊的距離其差值不會很大（大多數在lkm之內），這樣按標稱誤差的公式估算，兩條測邊的m，值和m。值非常接近，故對于精度的約算來說，從而可以來說兩條所測的測邊精度一樣或大約一樣，即：所以P點的誤差又可以寫成如下面的式子：

從以上的推導式子可以看出測邊后方會的影響因素主要由交會角度y、儀器的標稱精度以及所測的距離有關，具體是如何影響其精度也將在后面的實驗中呈現出來。

2.3 邊角同測后方交會的影響因素研究

將上式中的（7）式進一步簡化，得到如下式子：

從公式可以看出，邊角后方交會的精度與測角、測邊以及交會圖形有關，現在我們作以下式分析。

1）當y =90。時，此時m2，=oo，所以邊角后方交會測量中應當盡量避免三角形中并未測量的邊長與已知邊相垂直或者大約垂直。即y應避免在75。到90。之間的區域。

2）當y=0。時，此時m，的值最小，所以在邊角后方交會的布設圖形中其角度y應該< 30。為宜。當待定點P在已知邊上或者其延長線上的時候，m2，的值主要決定于值的大小。由極值理論知，當s1=s2時，s1與s2的相乘的結果最大，故當未知的點P在已知邊附近，且離已知點較近時候，為邊角同測的后方交會的最適宜布設點位的空間。

3）若取3=5+5 ppm，m=+10”，S。=l.Okm.可以計算不一樣的s1或s2以及y角所決定的邊角同測的后方交會圖形中的點位精度。故可畫出點位誤差的等值線圖。

3 實驗及數據分析

3.1 實驗概況

實驗實例：為了研究各后方交會中的影響因素時如何影響其精度的，現在在學校的西南角取實驗場地，按照以上原理方法現場模擬，按照圖1的圖形模擬實驗，用不同的方法取得不同的數據，按照公式求得未知點坐標，再研究其是如何變化，并繪制誤差等直線圖。

實驗的控制點和未知點的觀測均使用科利達全站儀儀器，且控制點坐標均為假設，該儀器經檢定達到使用精度的要求，并在有限期之內。其觀測角的精度為0 5”，測距的精度為0.5mm+lx 10-6d。

3.2 角度后方交會的分析

現按圖1的形狀假設儀器，分別測定三個方向值，從而就可以解算出夾角a，β。再按三角形基本知識進而求得S角度，由于m，的值可由K表示，如式K=將其轉為函數圖形表示。

當P點越過已知點C之后，誤差繼續增大，K值由4.8一直增大到無窮。當S =1700時，K=10.8。S=165。時，K=19.9。此后速度則迅速加快。P點從三角形中心點向危險圓移動時，在S=600β（P點在AB邊的直線上）之前，K值變化緩慢，越過AB線后K值的變化不斷加快，占- 800時，K80= 13.6。當P越過危險圓之后，誤差開始減小，S=1o0時，K1oo =20.4；在S=112.80時，K有最小值，且Kn2= 14.06。當S繼續增大，K值又迅速增大直至無窮。

由以上分析可知，在進行三點后方交會時，P點的位置選擇非常關鍵應避免危險圓附近區域以及遠離已知點的區域。

3.3 邊角后方交會的分析

將收集到的數據按公式解算出誤差結果，并繪制下表，如表1所示。

顧及到圖像的勻稱性以及操作的具體現場，采納圖2中的角度β為0?～180?，假設要求的邊長S2為已知邊的0-5倍；通過精度公式（β，S2，m），求得它們之間的關系，再以交會的角度β來作為縱軸，邊長S2來作為橫軸，并畫出誤差等值線圖，由圖形可以由如下分析。

1）當邊長S2的長度在低于已知邊的長度6倍時候，其角度β無論在什么范圍變動的時候，待定點P的中誤差的最大值都沒有超出120mm。

當角度β在0?～20?、60?～120?、160?～180?的范圍內的時候。未知點的點位誤差相對較小，并且與已知邊的邊長S2，大小沒有多大聯系。

當邊長S2是O～5倍的已知邊的長度時，角度B無論怎樣變化，未知點的誤差總是不超過±60mm。

當角度β在40。左右，邊長S2超過已知邊的邊長大約4倍的時候，未知點誤差相對較大；當角度β在132?左右，邊長S2超過已知邊的邊長大約4倍的時候，未知點誤差相對較大。角度誤差等值曲線圖中，相對集中的兩個空間內突現了較高的未知點的誤差。

4 結論

通過后方交會測量精度影響，所得到的主要結論如下。

1）在角度后方交會的測量中（三點后方交會），角度對其影響較大，其角度在30?～60?之間，未知點點位誤差較小；此外還與已知點的位置有一定的關系，當圖形對稱時精度較高。

2）在測邊后方交會測量中，可以看出，當邊長為已知的時候，其交會角y在90?～ll0?附近時候，未知點點位誤差較小；當角度一定時候，邊長選擇盡量選取短邊：

3）在進行邊角同測的后方交會中，故在待定的邊長與已知邊的邊長構成90?水平角的時候形成最佳圖像，這個時候待定點達到最佳的精度；當待定點與控制點的長度越小時，其精度越好。