最優潮流在電力系統中的最新應用綜述

貴州大學電氣工程學院　成　峰

?

最優潮流在電力系統中的最新應用綜述

貴州大學電氣工程學院成峰

【摘要】隨著電力系統的不斷發展，最優潮流問題在電力系統規劃、運行、控制等領域有著極為重要的意義。它的目標是在滿足一定等式和不等式約束前提下尋求該電力網控制變量的最優設定值，以達到一個或多個目標函數的最優化。本文主要從大規模交直流電網最優潮流和穩定約束最優潮流兩個方向總結了最優潮流的最新應用。

【關鍵詞】最優潮流；HVDC；TSCOPF；內點法；辛算法

1　引言

最優潮流(Optimal Power Flow, OPF)是電力系統規劃、運行和控制的核心問題。它的主要目標是在滿足一定等式和不等式約束前提下找到該電力網控制變量的最優設定值，以達到一個或多個目標函數的最優化。本文重點總結了電力系統最優潮流的最新應用，體現了國內外最新的研究動態。

2　最優潮流的最新應用

2.1大規模交直流電網最優潮流

由于我國客觀存在能源資源和電力需求的大跨度分布情況，迫使我國實施“西電東送、南北互供、全國聯網”的電力發展戰略。超高壓電網承擔了大范圍遠距離輸送電力的功能。而HVDC因為其傳輸距離長、線路造價低、線損少、不存在穩定問題、可實現非同步聯網等優點，在我國得到大規模應用。包括HVDC模型的潮流計算、OPF著力于對電網規劃運行評估以及提高經濟效益，是目前的熱點之一。

目前最優潮流計算中廣泛采取的HVDC模型大多來自文獻，其模型忽略了換流閥壓降和有功損耗以及換流變壓器功率損耗。因為國內采取的HVDC系統傳輸功率大，采取簡化模型已經無法滿足工程中的精度要求。文獻[1]給出HVDC系統的準穩態模型，準確計及了換流閥和換流變壓器上的損耗，并采取交直流系統交替求解的方法進行潮流計算，對交流系統采取標幺值計算，對直流系統采取有名值進行計算。文獻[2]將該模型進行恰當的簡化和標幺化處理，建立準確的含HVDC的最優潮流模型，并且采用罰內點法(penalty interior point method，PIPM)求解含HVDC最優潮流模型。其中的優化變量包含任一節點的有功、無功出力，無功補償出力，電壓幅值與相角以及直流變量。目標函數則取總有功出力最小。

文獻[2]經過算例得出PIPM 能在正常運行電壓約束下找到最優解，原因是：對應松弛量相當于在每一個節點增加了可調度負荷、發電機以及容許對母線電壓約束先進行松弛，PIPM 在這個迭代過程中逐步驅動松弛量趨于0。

然而大型交直流輸電網網損優化也是另一熱點。交直流并聯電網的網損優化與傳統無功優化有著很大區別，純交流電網主要通過合理配置系統無功用來降低網損，而交直流并聯電網則是通過調節直流功率改變有功潮流的分布，并將其轉移至交流通道，從而實現降低全網網損。現在區域特高壓交直流聯網已經是電網發展的重要方向。研究交直流電網網損優化理論具有十分重要的實際應用價值。

文獻[3]以南方電網為實例，其主網交直流通道送電水平超過20000MW，廠站無功配置的主要目標是保持通道電壓和提高系統穩定性，就目前來說采用交直流調整能夠給出的降損空間最為明顯。

調節直流輸送功率具有調節速度快、靈活等優點，因此大多用來改變系統潮流分布。然而，在調整直流功率時，做到保持各斷面不越限，保持電廠出力和各地區送受電計劃不變。交直流電網網損優化問題的數學模型如下：是直流系統網損；

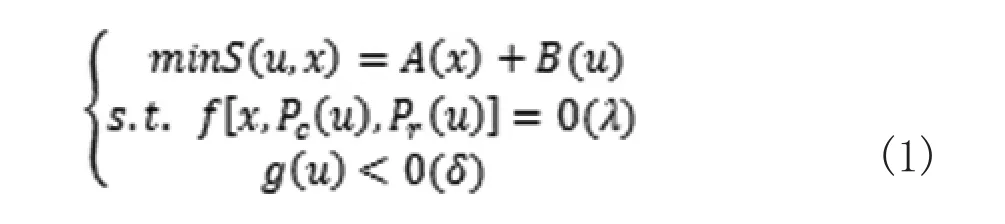
2.2穩定約束最優潮流

穩定約束最優潮流是電力系統運行與控制決策中的重要研究內容，其在最小化系統運行成本的同時，能夠通過調整穩態運行點，來提升系統受擾后的動態性能，包括暫態穩定性和短期電壓穩定性。最近幾年，為了維持電力系統在發生故障后的穩定，學者們將動態安全約束整合到常規OPF計算當中，從而構成了暫態穩定約束最優潮流(TSCOPF)，其同時考慮到了電力系統的動態安全性和經濟性，成為了一個研究熱點。

數學上TSCOPF問題在是一個含有微分代數方程約束的非線性規劃問題。由于含有微分方程，所以無法直接應用到常規的數學優化方法當中。

國內外學者提出了一些新的數值積分方法，從而為求解TSCOPF問題提供了新的方向。我國著名的數學家馮康提出了的針對哈密爾頓系統的辛幾何算法，簡稱辛算法。由于電力系統的具有龐大冗雜的特性，有學者提出了改進哈密爾頓系統辛幾何方法的建議。辛Gauss-Legendre Runge-Kutta(GLRK)方法是其中的一種，該方法是單步隱式方法，其計算精度高，數值穩定性好。有的將轉子運動方程變換成哈密爾頓正則方程的形式，采取四階辛GLRK的方法離散化該方程，確立了辛GLRK方法的TSCOPF哈密爾頓數學模型。然而在同樣的精度下條件，四階辛GLRK方法的步長是隱式梯形法的6倍。采用的TSCOPF模型，以有功網損最小為目標函數，其表達式為：

現代內點算法在電力系統中得到了廣泛的應用。但是，當系統規模龐大，其計算時間就會迅速延長，內存也將大量消耗，所以為了使得求解效率提高，可以采用減空間技術求解修正方程。原始–對偶內點法與減空間技術相結合能夠大大提高求解大規模TSCOPF問題的效率。

目前基于時域仿真信息的EEAC法，用于量化系統的暫態穩定性，已經應用在實際電網安全穩定量化評估的方法中。有文獻采用基于單機等值技術來進行暫態穩定評估，穩定性用穩定裕度和靈敏度來量化，這種方法能夠有效解決TSCOPF問題。也有采用等值后的功角門檻值約束與最優潮流結合，其計算相對簡便，但是存在系統穩定性不能采用功角門檻值來量化評估的問題。

文獻[5]采用的是將TSCOPF問題劃分為最優潮流、靈敏度分析和暫態穩定評估三個問題來迭代求解。最優潮流問題采用非線性原對偶內點法來求解，包括簡單穩定約束最優潮流。各穩定裕度的控制變量靈敏度通過軌跡靈敏度法來求解。暫態穩定評估采用EEAC法，同時得出不同穩定情況下的裕度表達式。然后添加矯正因子來避免過度調整，以達到穩定和經濟的協調。

基于EEAC理論等值后的模型為：

采用軌跡靈敏度能夠很好地分析系統參數對系統動態性能的影響，其包含的軌跡靈敏度方程與暫態時域仿真方程相仿，都是DAE方程，但是將軌跡靈敏度方程進行差分化之后就是線性方程，其可以提高求解速度，并且還可以進一步采用并行技術。文獻[5]采用的方法，綜合考慮了系統在不同穩定情況下通過調整來提高系統穩定裕度，從而實現暫態穩定約束的最優潮流計算，使得系統經濟運行。同時也考慮到了多擺失穩情況以及解決不同失穩模式下的多故障問題。

3　結語

最優潮流有著廣泛的應用場景，根據不同的應用場景，拓展不同的數學模型，比如更換部分約束條件和目標函數。隨著電力工業的發展，現代電網的規模和運行復雜程度日趨增加，最優潮流或許將作為一個子問題或者子模塊，通過設計一個大的迭代框架，選取合理的最優潮流算法，實現更復雜的問題，然而，最關鍵的問題將是如何高效而精確的求解最優潮流。

參考文獻

[1]鄭超,盛燦輝,郭小江,等.實用高壓直流輸電穩態模型及潮流算法解析[J].電網技術,2011,35(3):57-62．

[2]鄭華,李暉,肖晉宇,等.大規模交直流電網最優潮流模型與算法研究[J].中國電機工程學報,2015,35(9): 2162-2165.

[3]劉愷,陳亦平,張昆,等.大型交直流并聯輸電網網損優化理論及其在南方電網中的實現[J].中國電機工程學報,2014,34(1):130-135.

[4]劉鵬飛,韋化,李濱,等.基于哈密爾頓系統與辛算法的暫態穩定約束最優潮流[J].電網技術,2015,39(5): 1329-1334.

[5]趙晉泉,錢莉,陳剛.一種基于EEAC和軌跡靈敏度的暫態穩定約束最優潮流模型與方法[J].電力系統保護與控制,2015,43(9):9-12.

成峰（1989－），男，碩士研究生，研究方向為電力系統安全穩定與控制。

作者簡介：