電力系統廣域量測不良數據處理研究

周建平

摘 要：隨著我國經濟的不斷發展，電力系統規模日益擴大以及接線的復雜程度不斷上升，為了安全有效的輸送電能，需要保證電力系統的實時量測數據的準確性，同步相量測量技術是現代電力工業的最重要技術之一，基于GPS的時鐘同步相量量測單元（PMU）使得電力系統的實時電壓和電流相量的直接測量成為可能。由于PMU具有精度高、全網嚴格的時鐘同步、采樣周期短等優點，同步測量技術在電力系統狀態估計方面發揮著越來越重要的作用。該文研究基于PMU的量測信息存在不良數據的情況，提出一種處理不良數據的方法，對當前量測相量逐維地與歷史量測進行Kalman濾波計算，結合仿真計算，分析其在工程上的應用前景。

關鍵詞：同步測量 量測濾波 誤差

中圖分類號：TM744 文獻標識碼：A 文章編號：1672-3791（2015）11（a）-0029-03

狀態估計也稱為濾波，它通過電力系統實時量測的高度冗余來提高狀態估計精度，自動排除隨機噪聲形成的錯誤量測信息，估計出電力系統的運行狀態。當前電力系統中廣泛應用的數據采集和監控系統（SCADA），量測類型是電壓和功率型，但是SCADA系統量測精度還有待提高[1]。

近年來，國內外學者們對相角量測單元（Phasor Measurement Unit，PMU）及以其為基礎的廣域量測系統（Wide-Area Measurement System，WAMS）的關注越來越多[3]，PMU裝置用于同步相量測量和輸出以及動態記錄，基于標準時鐘信號的同步相量測量是PMU的重要特征之一[2-4]。利用這一核心特征，在更精細的時間尺度上對電力系統進行同步量測，這些帶時標量測數據也為智能調度系統中狀態估計提拱了全新的數據來源。

1 理論知識

1.1 基于PMU的線性靜態狀態估計

把PMU測量得到的節點電壓、支路電流相量作為量測值，基于PMU的算法利用直角坐標系進行計算，此時線性電力網絡量測方程可以有：

Z為維列量測相量，H為階的雅克比矩陣，雅克比矩陣為實數矩陣，僅僅支路參數和網絡開關狀態有關的矩陣，狀態量為除了平衡節點相角量測以外的（）維的列相量，為量測噪聲，為m 維列誤差相量。為該研究系統的節點個數，為量測值得個數。維的量測相量包括節點電壓和支路電流的實部和虛部[5]。

量測方程可寫成如下的分塊矩陣如公式

量測量有：節點電壓的實部量測和虛部量測、支路電流的實部和虛部。狀態變量為參考節點復數電壓的實部和其它所有節點的復數電壓的實部和虛部。雅克比矩陣為常數矩陣。

1.2 基于Kalman算法的量測濾波

該文沒有利用傳統的不良數據檢測與辨識方法對不良數據尋找并剔除，直接利用歷史量測值對當前量測值進行濾波。通過Kalman濾波算法對量測數據的一個時間斷面進行研究，利用歷史量測值作為預報值與當前量測值進行濾波計算，且基于一維數據（一個量測相量中的每一個一維數據）進行。該文詳細研究一維的Kalman濾波，以及基于一維Kalman濾波的應用。

上式中為當前時刻的系統量測值的第個數值；為上一時刻的量測相量第個數字；為經過Kalman濾波計算得到的當前時刻的量測濾波相量的第值；為歷史量測相量第個數值所加高斯白噪聲的方差；為當前量測相量第個數值所加高斯白噪聲的方差；為Kalman濾波計算得到的當前時刻的量測濾波相量的第值所加高斯白噪聲的方差。維相量為對應于此量測值權值矩陣的對角元素。

2 仿真計算及結果分析

該算例在IEEE14節點上運行，由于該算法是在時間斷面上研究的，因此這里暫不研究該算法在動態狀態估計中的應用，本章研究線性靜態狀態估計的量測濾波效果，以及量測濾波前后狀態估計效果。

算例中選取5組量測質量較好的歷史量測值，5組量測值分別在一維的層面進行Kalman量測濾波，將五個量測值依次濾波得到的新的量測相量在與當前的量測進行Kalman量測濾波，濾波結果作為最終量測值來計算狀態估計值。該算例中五組不同的歷史量測值加零均值0.01方差的正態分布誤差；當前量測值中存在壞數據，在第29到49個量測中加零均值0.1方差正態分布噪聲（此部分即為當前量測中存在的錯誤數據），其余部分量測數據加零均值0.01方差的正態分布誤差。利用兩種量測相量在一維層面上進行Kalman濾波，這樣得到的即為最終用于狀態估計的量測相量。

以下的仿真結果圖中，將從濾波前后的量測量與真值相比的絕對誤差、濾波前后的量測分別進行狀態估計結果的絕對誤差兩方面來研究本章提出算法的計算效果。下面為仿真計算結果圖和結果分析。

（1）當前各量測值的絕對誤差、當前量測值與歷史量測值濾波之后量測數據的絕對誤差曲線如圖1所示。

分析：

如圖1所示，正方形的節點曲線代表當前量測值中存在錯誤部分經過濾波后得到的量測值與量測真實值之間的絕對誤差，三角形節點曲線代表的是當前量測值中存在錯誤部分與真實量測值之間的絕對誤差。從仿真結果圖中可以清晰的得到在經過歷史量測值進行Kalman濾波計算之后，當前量測值的平均絕對誤差有著明顯的減小，這說明了經過Kalman算法的量測濾波計算對于糾正量測錯誤有著很好的效果。下面將利用當前量測值在濾波前后的量測量分別計算線性靜態狀態估計，根據兩種線性靜態狀態估計的結果對比本章提出算法在量測量糾錯方面的性能。

（2）分別利用當前量測值經過濾波處理前后的量測值進行線性靜態狀態估計計算，研究比較狀態估計的計算結果。

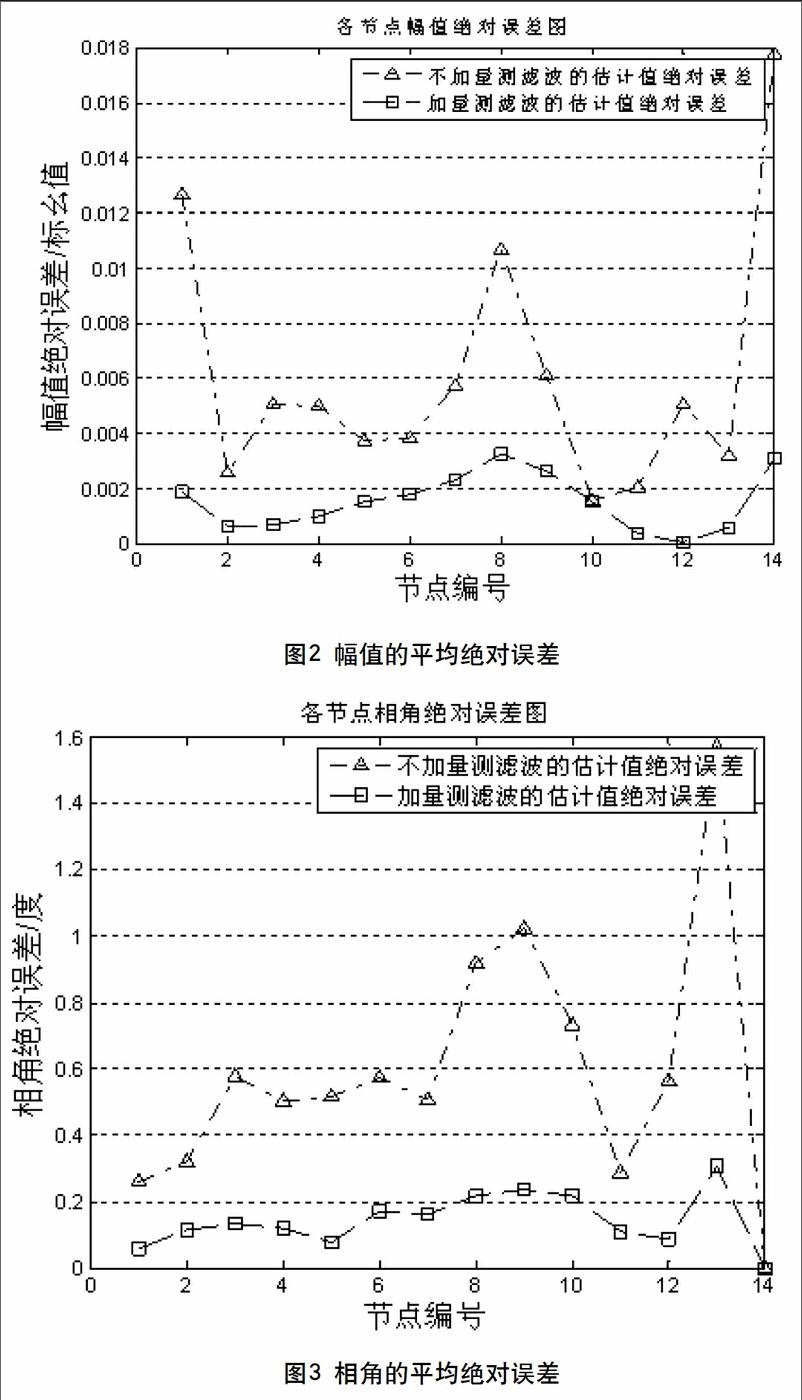
狀態量真值幅值、直接利用量測進行的狀態估計結果幅值、量測濾波后的狀態估計幅值、相角平均絕對誤差如圖2、圖3所示。

狀態估計幅值的平均絕對誤差如圖2。

每個節點的相角平均絕對誤差如圖3。

當前量測值在經過Kalman量測濾波前后的狀態量幅值和相角的平均絕對誤差如表1所示。

分析：

由圖2～圖5和表1可知，在量測絕對誤差曲線圖中得出量測量的絕對誤差在Kalman濾波后有著明顯的減小。表3.1中得到濾波之后進行線性靜態狀態估計得到的量測進行線性靜態狀態估計計算得到的幅值和相角的平均絕對誤差有顯著的減小。因此，本文研究的基于Kalman算法的量測濾波計算方法效果明顯，在一維層面逐個數字濾波對量測量的糾錯能力顯著。

3 結語

該文提出一種新的不良數據處理方法：基于Kalman算法的量測濾波，不同于傳統意義上的不良數據檢測和辨識，該算法利用多組較為準確的歷史數據多次濾波計算之后，得到較為合理的量測濾波數據對當前量測進行Kalman濾波，沒有經過檢測與辨識的過程，直接替換不良數據，取得了良好的不良數據處理效果。

該文的仿真算例僅在IEEE14節點的數據上進行的，沒有在更多節點或者大電網中仿真運行，工程中的應用效果還需進一步研究，該文研究廣域量測系統必須所有節點裝設PMU，這使得工程造價太高，使得推廣具有一定的難度。

參考文獻

[1] 于爾鏗.電力系統狀態估計[M].北京： 水利電力出版社，1985.

[2] 李碧君，薛禹勝，顧錦汶，等.電力系統狀態估計問題的研究現狀和展望[J].電力系統自動化，1998，22（11）：53-60.

[3] Azevedo G P，Oliveria Filho A L.Control centers with open architectures[J].IEEE Computer Application in Power，2001，14（4）：27-32.

[4] 李強，周京陽，于爾鏗，等.基于向量量測的電力系統線性狀態估計[J].電力系統自動化.2005，29（18）：24-28.

[5] Zhang B M，Lo K L.Recursive measurement error estimation identification method for bad data analysis in power system state estimation [J].IEEE Transactions on Power Systems，1991，6（1）：191-198.