微慣性/衛星組合導航系統算法研究

石 拓，陳家斌，田曉春，宋春雷,楊黎明，尹靜源

(1.中電54所，石家莊 050081；2.北京理工大學自動化學院，北京 100081;.華北光學儀器有限公司，北京 100053；4.北京機電工程總體設計部，北京 100039)

微慣性/衛星組合導航系統算法研究

石 拓1,2，陳家斌2，田曉春2，宋春雷2,楊黎明3，尹靜源4

(1.中電54所，石家莊 050081；2.北京理工大學自動化學院，北京 100081;.華北光學儀器有限公司，北京 100053；4.北京機電工程總體設計部，北京 100039)

微慣導系統(MINS)與衛星導航系統(GNSS)的結合不僅可以充分利用微慣導系統良好的短期性能和GNSS的長期穩定性，彌補MINS系統誤差隨時間積累和GNSS采樣頻率低、動態性能差的缺陷，而且使得組合導航系統的精度和動態能力同步提高，保證了系統在衛星信號受遮擋或失效的環境下仍能夠以較高的精度自主運行一段時間，正常工作。采用星網宇達的產品采集真實數據進行了離線仿真，比較了多種濾波算法，實驗證明，采用UKF取得的效果最好，EKF次之，KF最差。

微慣導；組合導航；Kalman濾波

0 引言

隨著微機電系統(Micro-Electro-Mechanical System，MEMS)技術的日漸成熟，以及微型飛行器、微型機器人等微小型設備的廣泛應用，低成本、小型化、低功耗的微慣性器件發展迅速[1-2]。微機電慣性導航系統(MEMS Inertial Navigation System,MINS)是指基于MEMS技術的慣性測量單元，是一種集成化的微型捷聯慣導系統，與之前常用的慣性器件不同，MINS在保證測量精度不明顯下降的前提下，體積和質量更小、成本更低。正是由于MINS系統的這些優點，使得MINS/全球導航衛星系統(Global Navigation Satellite System，GNSS)組合導航成為近年來研究的熱點。

1 組合導航系統數學模型

對于MINS/GNSS組合導航系統，建立準確的濾波數學模型是采用濾波技術進行組合的基礎。根據姿態誤差(失準角)估計值的大小不同，可以將組合導航系統濾波數學模型分為線性模型和非線性模型[3]。在車載環境下，可將姿態誤差角視為兩種情況：一種是將三個姿態誤差角都看成小角，建立線性模型；另一種是將俯仰角和橫滾角看成小角，而將航向角看成大失準角，建立非線性模型。

設組合導航系統的狀態變量為

XI= [φEφNφUδvEδvNδvUδLδλ

取MINS和GNSS輸出的位置和速度之差作為組合導航系統的觀測量。

1.1 線性系統的數學模型

對于線性系統，設其狀態方程為

系統噪聲向量由陀螺儀和加速度計的隨機誤差組成，表達式為

其中，FN為對應的9維基本導航參數矩陣，其非零項可由下述誤差方程確定。

由于姿態誤差角為小角度，即有[4]

則姿態誤差方程為:

式中，下角標E、N、U分別為地理坐標系東、北、天3個方向；RM為當地子午面內主曲率半徑；RN為與子午面垂直平面上的主曲率半徑；L為地理緯度；λ為地理經度；h為地理高度；ωie為地球自轉角速度。

速度誤差方程為:

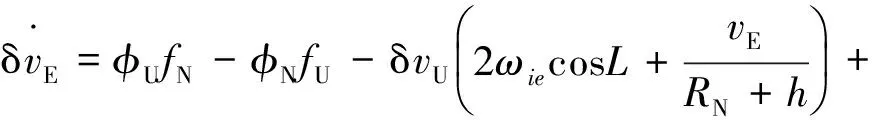
式中，fE、fN、fU為加速度計輸出在導航坐標系下的投影。

位置誤差方程為:

FS和FM的取值如下

1.2 非線性系統的數學模型

對于非線性系統設其狀態方程為

車載環境下，通常俯仰角和橫滾角為小角，航向角為大失準角，即有

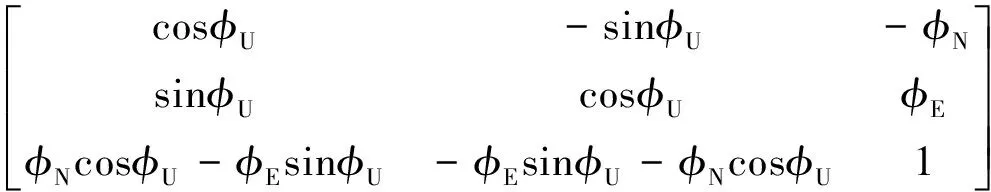
則姿態誤差方程為:

深化市縣機構改革，夯實基層基礎。市縣機構改革必須面向人民群眾、符合基層事務特點，在職能配置上更加突出民生，強化社會管理和公共服務職能，在機構設置上不簡單照搬上級機關設置模式，既允許“一對多”，也允許“多對一”，確保上下貫通，執行有力。全面落實鄉鎮、街道相關改革，統籌推進第二批經濟發達鎮行政管理體制改革，實行扁平化和網格化管理，使各類機構、組織在服務保障群眾需求上有更大作為。

sinφUεE-cosφUεN

位置誤差與慣性器件誤差與線性系統相同，這里不再贅述。

取SINS和GNSS輸出的位置和速度之差作為量測量，其中，速度量測矢量為

式中

位置觀測矢量為

其中

上述各式中，vGE、vGN、vGU為GNSS沿東北天方向上的速度誤差；NGE、NGN、NGU為GNSS沿東北天方向上的位置誤差。

聯合速度和位置量測方程，組合導航的量測方程為

2 組合導航系統離線仿真

本車載實驗是在北京理工大學中關村校區附近進行的，跑車路線是圍繞北京理工大學中關村校區順時針1周，起點和終點都是北京理工大學北門。實際路線如圖1所示。

圖1 實驗跑車路線Fig.1 Experiment path

本實驗儀器選用北京星網宇達科技股份有限公司所研發的慣性/衛星組合導航系統，根據該公司提供的軟件，可以分別設置慣導和衛星的數據輸出頻率。本實驗設定全球定位系統(GlobalPositioningSystem，GPS)的采樣頻率為0.5Hz，MINS的采樣頻率為50Hz。

實驗將GPS給出的速度和位置與慣導解算出的速度和位置作差作為觀測量，用Kalman濾波(KF)估計出系統的誤差，再對慣導系統進行補償。

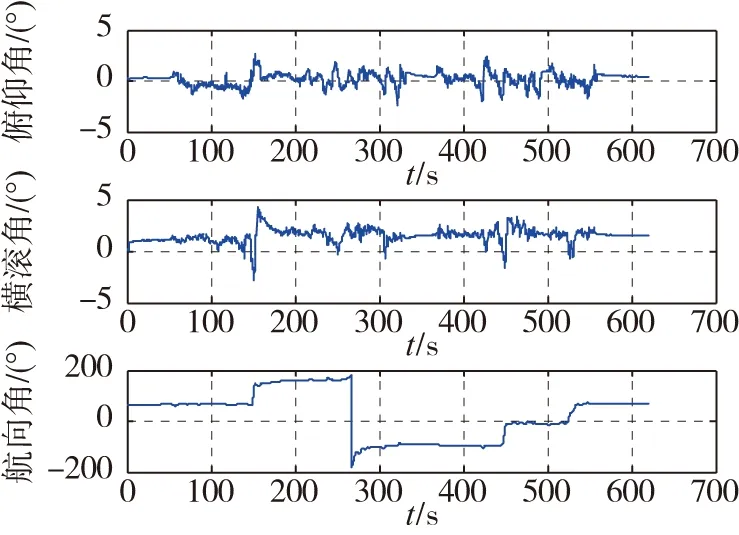
圖2 KF組合姿態Fig.2 KF combined attitude

圖3 KF組合速度Fig.3 KF combined speed

圖4 KF組合位置Fig.4 KF combined position

圖2～圖9所示為運用標準KF進行組合導航得到的結果。由圖2可以看出，組合后的俯仰角和橫滾角變化在3°左右，明顯小于純慣導解算的結果。圖4所示為位置解算結果，紅色代表GPS跑車路線，藍色代表組合后的跑車路線，可以看出，組合后的位置比單獨GPS給出的位置平滑很多，如在圖中下部等紅燈階段，GPS數據產生了微小的跳變，而組合之后位置曲線很平滑，并且在GPS丟星的時間里，組合系統運用純慣導數據進行解算，雖然存在一定的誤差，但大致方向正確。圖5所示為濾波估計出的姿態誤差，可以看出俯仰角和橫滾角誤差最大在2°左右，但是航向角誤差較大，最大值在5°左右。圖6所示為濾波估計出的速度誤差，水平方向的最大值在5m/s左右，天向能達到20m/s。濾波后的位置誤差如圖7所示，在GPS信號良好的情況下，組合導航的位置誤差在5m以內；在無法獲得衛星信號的大約20s時間段內，系統由微慣導導航，緯度誤差達到了15m，經度誤差約為25m，高度誤差超過200m。另外組合導航系統還經過KF估計出了陀螺的常值漂移為100(°)/h，加速度計零偏為10mg。

圖5 KF姿態角誤差Fig.5 KF attitude error

圖6 KF速度誤差Fig.6 KF speed error

圖8 陀螺常值漂移Fig.8 Gyro drift

圖9 加計零偏Fig.9 Accelerometer bias

論文基于大方位失準角條件下的非線性誤差方程，分別設計了擴展Kalman濾波(EKF)和無跡Kalman濾波(UKF)兩種非線性濾波方法，仿真結果如圖10～圖17所示。

圖10 EKF組合位置Fig.10 EKF combined position

圖11 EKF姿態誤差Fig.11 EKF attitude error

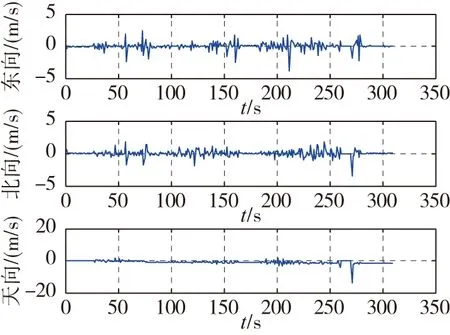
圖12 EKF速度誤差Fig.12 EKF speed error

圖13 EKF位置誤差Fig.13 EKF position error

圖14 UKF組合位置Fig.14 UKF combined position

圖15 UKF姿態誤差Fig.15 UKF attitude error

圖16 UKF速度誤差Fig.16 UKF speed error

圖17 UKF位置誤差Fig.17 UKF position error

圖10～圖13所示為采用EKF方法進行組合導航的結果。圖11所示的姿態角誤差可以看出俯仰角和橫滾角誤差最大在1°左右，小于圖5所示的結果，航向角也相對較小；水平方向的速度誤差最大值在3m/s左右，天向也減小到15m/s。

圖14～圖17所示為采用UKF方法進行組合導航的結果。雖然姿態誤差沒有明顯的提升，但速度誤差和位置誤差都有較好的結果。從圖17所示的位置誤差可以看出，UKF濾波后的緯度誤差在20m左右，經度誤差在10m以內，高度誤差縮小到了100m以內，使得丟星后的定位誤差有較大的提升。

3 結論

由以上分析可以看出，丟星之前采用KF、EKF和UKF方法進行組合導航都可以較好地完成導航任務，丟星后UKF定位精度最高，EKF次之，KF效果最差。

[1] 閆鑫. 基于抗差估計的GPS/MIMU組合導航濾波算法研究[D].哈爾濱: 哈爾濱工程大學,2010.

[2] 黃麗斌.MINS/GPS組合導航系統算法研究[D].南京:東南大學, 2004.

[3] 全偉, 劉百奇, 宮曉琳, 等. 慣性/天文/衛星組合導航技術[M].北京: 國防工業出版社, 2011.

[4] 秦永元. 慣性導航(第二版)[M].北京：科學出版社, 2014.

[5] 付夢印,鄧志紅, 閆麗萍.Kalman濾波理論及其在導航系統中的應用(第二版)[M].北京:科學出版社,2010.

[6] 嚴恭敏.捷聯慣導算法及車載組合導航系統研究[D].西安: 西北工業大學, 2004.

[7] 謝鋼.GPS原理與接收機設計[M].北京: 電子工業出版社, 2009.

[8] 王君帥, 王新龍.SINS/GPS緊組合與松組合導航系統性能仿真分析[J], 航空兵器, 2013(2): 14-19.

[9]GodhaS,CannonME.GPS/MEMSINSintegratedsystemfornavigationinurbanareas[J].GPSSolutions, 2007, 11(3):193-203.

[10]SolovievA.TightcouplingofGPS,INS,andlaserforurbannavigation[J].IEEETransactionsonAerospaceandElectronicSystems, 2010, 46(4): 1731-1746.

[11] 應士君, 李金金, 劉衛, 等.BD-2/GPS組合導航系統選星算法及定位分析[J].上海海事大學學報, 2013, 34(2): 1-4.

[12]BrennerM.IntegratedGPS/inertialfaultdetectionavailability[C]//ProceedingsofIONGPS,PalmSprings,CA, 1995.

[13] 劉華, 劉彤, 張繼偉. 陸地車輛GNSS/MEMS慣性組合導航機體系約束算法研究[J].北京理工大學學報, 2013, 33(5): 500-515.

[14] 張光理. 北斗/SINS組合導航系統研究[D].哈爾濱工程大學, 2012.

Algorithm Research on MINS/GNSS Integrated Navigation System

SHI Tuo1,2, CHEN Jia-bin2, TIAN Xiao-chun2,SONG Chun-lei2, YANG Li-ming3, YIN Jing-yuan4

(1.CETC 54, Shijiazhuang 050081, China;2.School of Automation, Beijing Institute of Technology, Beijing 100081, China;3.North China Optical Instrument Co., Ltd.,Beijing 100053, China;4. Beijing Electro-mechanical Engineering System Design Department, Beijing 100039, China)

Micro inertial navigation system(MINS) with the combination of the Global navigation satellite system (GNSS) can make full use of the short-term performance of MINS and the long-term stability of the GNSS.It can make up for the defects of error accumulated over time of MINS, and for the low sampling frequency and poor dynamic performance of GNSS. Thus, it can improve the precision and dynamic capabilities of integrated navigation system, and it can also ensure the system to operate a period of time autonomously at high precision when the satellite signal is shielded or failure. We use StarNeto products to collect real data and compare a variety of filtering algorithms. Experimental results show that the effect achieved by UKF is best, EKF followed, KF worst.

MINS; Intergrated navigation; Kalman filter

10.19306/j.cnki.2095-8110.2016.06.006

2015-09-19；

2015-10-29。

石拓(1989 - )，男，碩士，主要從事衛星與慣性組合導航技術方面的研究。E-mail: shituo5858@126.com

U666.11

A

2095-8110(2016)06-0026-07