數(shù)據(jù)場和K-Means算法融合的雷達(dá)信號分選

， ， ，

(中國人民解放軍93199部隊(duì)， 黑龍江哈爾濱 150001)

0 引言

雷達(dá)信號分選是雷達(dá)偵察系統(tǒng)中信號處理的核心部分之一，只有從交疊信號流中分選出各個輻射源脈沖序列之后才能進(jìn)行信號參數(shù)的測量、分析、識別以及對威脅輻射源施加干擾。傳統(tǒng)采用脈沖重復(fù)間隔(PRI)單參數(shù)分選的正確率較低，已經(jīng)不能適應(yīng)當(dāng)前復(fù)雜的電磁環(huán)境。聚類分析作為數(shù)據(jù)挖掘中的一種重要技術(shù)，近年來成為眾多學(xué)者研究的熱點(diǎn)，有很多學(xué)者嘗試著將其應(yīng)用于雷達(dá)信號分選領(lǐng)域，取得了一些成績。國內(nèi)學(xué)者在聚類分選方法上也作了不少研究，代表性的有許丹[1]探討了在單站無源定位條件下當(dāng)測角精度不高時的信號分選問題，提出了一種二次聚類方法。2005年我國著名信號分選專家祝正威提出了一種針對未知雷達(dá)信號的加權(quán)動態(tài)聚類分選算法[2]，該方法雖然在一定程度上解決了密集復(fù)雜脈沖信號的分選問題，但是仍然無法解決長期以來一直面臨的“容差”問題。另外，文獻(xiàn)[3-6]中分別研究了基于模糊聚類、BFSN聚類、基于分段聚類和基于網(wǎng)格聚類在雷達(dá)信號分選中的應(yīng)用。張萬軍使用K-Means聚類對參數(shù)相近、互相交疊的非常規(guī)雷達(dá)信號進(jìn)行分選，效果較好、速度快，但是K-Means聚類算法需要先驗(yàn)知識，不適合未知雷達(dá)信號的分選。

針對K-Means聚類算法的缺陷，本文提出了一種融合算法，將數(shù)據(jù)場算法與其相結(jié)合，利用數(shù)據(jù)場對雷達(dá)數(shù)據(jù)流進(jìn)行初分選，得到初始的聚類中心和聚類數(shù)目，然后利用K-Means聚類完成最后的分選。

1 K-Means聚類算法原理

K-Means聚類算法由MacQueen首先提出，屬于聚類方法中一種基于劃分的方法，它是一種較簡單的迭代優(yōu)化方法。該算法的數(shù)學(xué)描述如下：

這種聚類算法的特點(diǎn)是：每個類都是全體數(shù)據(jù)對象的一個子集或者真子集，其中每個數(shù)據(jù)對象到定義該類的聚類中心的距離比到其他類聚類中心的距離更近，在已知聚類個數(shù)k的情況下，對樣本集合進(jìn)行聚類，聚類的結(jié)果由k個聚類中心來表達(dá)，基于給定的聚類目標(biāo)函數(shù)或者說是聚類效果判別準(zhǔn)則，算法采用迭代更新的方法，每一次迭代過程都是向目標(biāo)函數(shù)值減小的方向進(jìn)行，最終達(dá)到較好的聚類效果。

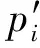
2 數(shù)據(jù)場聚類原理

李德毅院士在傳統(tǒng)物理場的基礎(chǔ)上，提出了基于數(shù)據(jù)對象的數(shù)據(jù)場理論。數(shù)據(jù)場能夠合理、客觀地展示數(shù)據(jù)對象間的相互影響和相互作用[7]。該理論[8-9]認(rèn)為數(shù)域空間中每個數(shù)據(jù)點(diǎn)都是一個有作用域的場，即每個數(shù)據(jù)點(diǎn)可以作用周圍其他數(shù)據(jù)點(diǎn)，用勢函數(shù)表示這種作用力。場中數(shù)據(jù)點(diǎn)之間都通過勢函數(shù)互相作用，其作用力的大小與兩者之間距離成反比。數(shù)學(xué)描述如下：

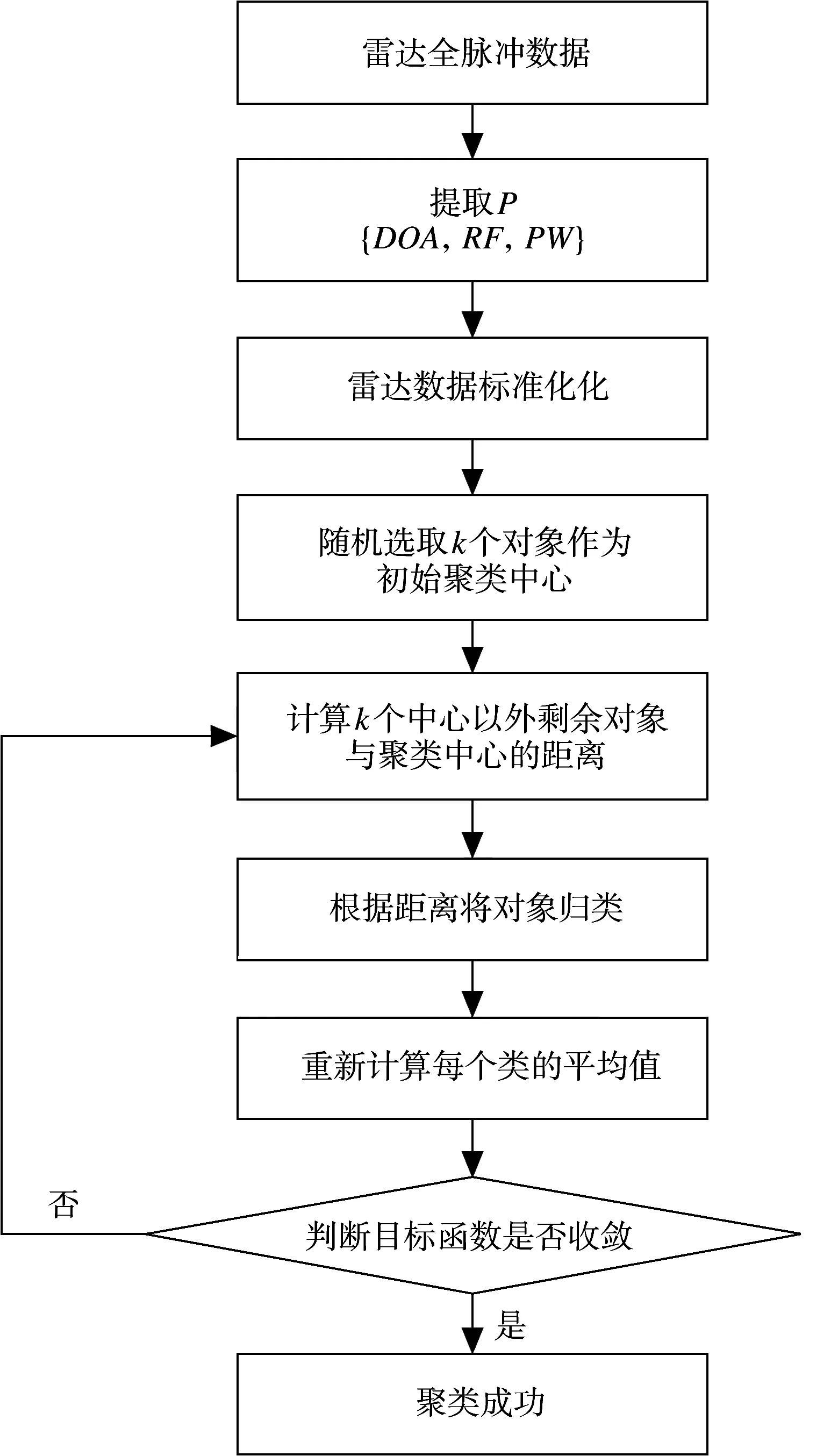
圖1 K-Means雷達(dá)信號聚類分選算法流程圖

定義數(shù)據(jù)場空間Ω∈Rn，其空間Ω為包含n個對象的數(shù)據(jù)集D={x1,x2,x3,…,xn}及其產(chǎn)生的數(shù)據(jù)場。設(shè)數(shù)據(jù)對象的位置矢量分別為x1,x2,x3,…,xn，對于Ω中任意一個場點(diǎn)y，其產(chǎn)生的勢函數(shù)為φ(y)，本文選用的是高斯函數(shù)，場強(qiáng)矢量值為F(y)，表示分別如下：

(1)

(2)

式中，‖y-xi‖為點(diǎn)y到xi的距離，本文選擇的是歐幾里得距離；mi≥0(i=1,2,3,…,n)為對象xi的質(zhì)量，這里簡化為單位質(zhì)點(diǎn)即mi=1；δ為輻射因子，用于控制對象間的作用力程。在空間Ω中，由于數(shù)據(jù)點(diǎn)勢函數(shù)的存在，數(shù)據(jù)點(diǎn)間在無外力作用下會發(fā)生相向運(yùn)動，但受δ的約束，δ越大，所有數(shù)據(jù)點(diǎn)的影響力越大，輻射范圍的影響也越大，則數(shù)據(jù)場的視圖越能體現(xiàn)所有數(shù)據(jù)點(diǎn)所產(chǎn)生勢場的總體效果；δ越小，所有數(shù)據(jù)點(diǎn)的影響力越小，輻射范圍的影響也越小，則數(shù)據(jù)場的視圖越能體現(xiàn)每個數(shù)據(jù)點(diǎn)所單獨(dú)產(chǎn)生影響的效果。

3 融合算法

K-Means聚類算法[10-11]應(yīng)用到雷達(dá)信號分選中，適合處理大量數(shù)據(jù)，聚類時間短，但是存在需要事先確定初始聚類中心和聚類數(shù)目的缺陷。選擇的初始聚類中心越接近最終的聚類中心，聚類效果越好，迭代時間越短。而數(shù)據(jù)場聚類算法恰好無需數(shù)據(jù)的先驗(yàn)知識就能完成初始聚類，提供K-Means聚類算法所需的先驗(yàn)知識。針對兩種算法的特點(diǎn)，本文將兩種聚類算法相結(jié)合，首先利用數(shù)據(jù)場聚類數(shù)目作為K-Means的初始聚類數(shù)目，數(shù)據(jù)場聚類得到的勢中心作為K-Means聚類算法的初始聚類中心，最后由K-Means聚類算法完成最后的聚類。

1) 雷達(dá)數(shù)據(jù)標(biāo)準(zhǔn)化

在實(shí)際的雷達(dá)信號分選中，收到的雷達(dá)信號數(shù)據(jù)流往往比較復(fù)雜，不同參數(shù)往往不在同一數(shù)量級上[12]。為了消除原始數(shù)據(jù)對分選的影響，需要對雷達(dá)信號數(shù)據(jù)流進(jìn)行預(yù)處理，使其分布在[0,1]之間，以相同數(shù)量級進(jìn)行分選。

(3)

(4)

2) 雷達(dá)信號分選的流程

① 初始化算法參數(shù)；

② 讀入雷達(dá)脈沖數(shù)據(jù)，提取雷達(dá)信號參數(shù)脈動到達(dá)角DOA、脈沖載頻RF和脈沖寬度PW進(jìn)行數(shù)據(jù)標(biāo)準(zhǔn)化處理；

③ 利用數(shù)據(jù)場聚類進(jìn)行初始的聚類，得到聚類數(shù)目和勢中心；

④ 利用K-Means聚類算法進(jìn)行聚類，輸出結(jié)果。

4 仿真實(shí)驗(yàn)分析

為了驗(yàn)證本文提出的融合算法是否有效，仿真實(shí)驗(yàn)?zāi)M了3部復(fù)雜體制的雷達(dá)數(shù)據(jù)，按照到達(dá)時間進(jìn)行混合，對同時到達(dá)的信號進(jìn)行丟失處理，共得到230個脈沖信號。實(shí)際接收的雷達(dá)數(shù)據(jù)與接收機(jī)接收的數(shù)據(jù)有不可避免的測量誤差，所以在模擬雷達(dá)數(shù)據(jù)時，給每個參數(shù)加上一個隨機(jī)偏差，參數(shù)的偏差均在1%以內(nèi)。模擬的雷達(dá)信號參數(shù)如表1所示。

表1 雷達(dá)仿真數(shù)據(jù)

3部雷達(dá)混合數(shù)據(jù)經(jīng)過標(biāo)準(zhǔn)化處理后，分布如圖2所示(圖中“*”代表雷達(dá)脈沖)。

圖2 雷達(dá)混合數(shù)據(jù)三維屬性分布圖

經(jīng)過數(shù)據(jù)場聚類初分選后的效果如圖3所示。

(a)RF-DOA數(shù)據(jù)場勢圖

(b)PRI-DOA數(shù)據(jù)場勢圖

(c)PRI-RF數(shù)據(jù)場勢圖圖3 數(shù)據(jù)場聚類初分選效果圖

經(jīng)過K-Means最后聚類分選效果如圖4所示，圖中不同形狀代表了聚類后的不同雷達(dá)數(shù)據(jù)。

(a)雷達(dá)混合數(shù)據(jù)分選效果分布圖

(b)分選數(shù)據(jù)統(tǒng)計結(jié)果圖4 融合算法雷達(dá)信號分選效果圖

由圖4分析可以發(fā)現(xiàn)，本文提出的融合聚類算法將雷達(dá)B中的10個脈沖誤分選為雷達(dá)A，與雷達(dá)A的脈沖一起標(biāo)記為雷達(dá)A；將雷達(dá)B中的30個脈沖誤分選為雷達(dá)C，其余脈沖均分選正確。統(tǒng)計后算得分選正確率為89.74%。

本文將同組雷達(dá)數(shù)據(jù)利用數(shù)據(jù)場聚類算法和K-Means聚類算法進(jìn)行了處理，對比結(jié)果如表2所示。

表2 分選算法對比結(jié)果

由于K-Means聚類算法需要事先給定好聚類數(shù)目，而且初始值的選定對聚類結(jié)果影響很大，所以本實(shí)驗(yàn)對K-Means進(jìn)行了100次實(shí)驗(yàn)得到的數(shù)據(jù)均為平均值。

由表2可以看出，K-Means聚類算法用時最短，但是其平均聚類準(zhǔn)確率比較低；融合分選算法在3種算法中準(zhǔn)確率最高，用時最多。

5 結(jié)束語

本文將數(shù)據(jù)場引入到雷達(dá)信號分選中，將其與K-Means聚類算法相結(jié)合，利用了數(shù)據(jù)場無需先驗(yàn)知識聚類的優(yōu)勢。經(jīng)過本文的仿真實(shí)驗(yàn)驗(yàn)證，本文提出的融合算法對復(fù)雜的雷達(dá)信號具有良好的分選效果，具有一定的應(yīng)用價值，缺點(diǎn)是分選時間較長。本文只是針對幾種特殊體制雷達(dá)信號進(jìn)行了仿真實(shí)驗(yàn)，后續(xù)還需要加強(qiáng)對其他復(fù)雜體制雷達(dá)信號的研究。

[1] 許丹,姜文利,周一宇. 輻射源脈沖分選的二次聚類方法[J]. 航天電子對抗, 2004(3):26-29.

[2] 祝正威. 雷達(dá)信號的聚類分選方法[J]. 電子對抗, 2005(6):6-10.

[3] 王勇剛. 基于模糊聚類的雷達(dá)信號分選方法[J]. 電子對抗, 2007(2):9-12.

[4] 葉菲,羅景青. 基于BFSN聚類的雷達(dá)信號分選與特征提取算法[J]. 艦船電子對抗, 2005, 28(3):29-34.

[5] 國強(qiáng),王常虹,郭立民,等. 分段聚類在雷達(dá)信號分選中的應(yīng)用[J]. 北京郵電大學(xué)學(xué)報, 2008, 31(2):132-135.

[6] 詹磊,唐愛華. 基于多維加權(quán)聚類的雷達(dá)信號分選方法[J]. 遙測遙控, 2007, 28(S1):113-117.

[7] 陳少達(dá),夏士雄,王志曉. 基于改進(jìn)譜聚類的提升機(jī)故障診斷算法[J].計算機(jī)工程與設(shè)計, 2015,

36(12):3241-3245.

[8] 劉玉華,張翼,徐翠,等. 一種基于數(shù)據(jù)場的復(fù)雜網(wǎng)絡(luò)聚類算法[J]. 計算機(jī)科學(xué), 2013, 40(11):70-73.

[9] 王麗紅,何熊熊. 基于數(shù)據(jù)場的FCM改進(jìn)算法[J]. 計算機(jī)與現(xiàn)代化, 2014(6):94-97.

[10] YANG Zhutian, WU Zhilu, YIN Zhendong, et al. Hybrid Radar Emitter Recognition Based on Rough K-Means Classifier and Relevance Vector Machine[J]. Sensors, 2013, 13(1):848-864.

[11] 關(guān)欣,孫祥威,曹昕瑩. 改進(jìn)的K-Means算法在特征關(guān)聯(lián)中的應(yīng)用[J]. 雷達(dá)科學(xué)與技術(shù), 2014, 12(1):81-85.

[12] 趙貴喜,王巖,于冰,等. 基于人工魚群聚類的雷達(dá)信號分選算法[J]. 雷達(dá)科學(xué)與技術(shù), 2013, 11(4):375-378.