基于SARIMA的我國汽車銷量預測分析

王旭天　李政遠　舒慧生

[摘要]汽車工業在國民經濟中占有重要地位，準確預測汽車銷量具有十分重要的意義。由于假日及其他因素影響，汽車的月度銷售數據表現出季節性的特征。文章選用我國2004年1月—2015年1月的汽車月度銷售數據為研究對象，構建了具有季節調整的ARIMA模型并用于銷量預測，預測結果的平均相對誤差可控制在3%以內，模型合理有效，具有良好的參考價值。

[關鍵詞]ARIMA模型；汽車銷量；SARIMA預測

[DOI]10.13939/j.cnki.zgsc.2016.01.071

1 引 言

隨著我國經濟的快速發展和居民生活水平的提高，汽車在人群中開始逐漸普及，成為許多人的生活必需品。與此同時，汽車工業迅速發展，在國民經濟中也扮演著越來越重要的角色，與機械電子、石油化工和建筑業一道構成了我國經濟的四大支柱產業，因而如何對汽車銷量進行準確的預測具有重要意義。

ARIMA模型是20世紀70年代由博克斯和詹金斯提出的時間序列方法[1][2]，所以又被稱為博克斯-詹金斯法，其全稱是自回歸積分滑動平均模型（Autoregressive Integrated Moving Average Model），包含移動平均過程（MA）和自回歸過程（AR）兩個部分。ARIMA模型發展至今理論已非常成熟，在實踐中應用廣泛。如龔承剛，王夢等人將ARIMA模型運用到了對湖北省城鄉居民收入差距的預測中，預測到未來三年湖北省的城鄉居民收入差距比仍處在較高水平。[3]薛蓓蓓運用ARIMA模型對安徽省固定資產投資總額進行了建模和預測，借助Eviews軟件給出了短期的預測值。[4]張麗，牛惠芳將SARIMA模型運用到了對我國CPI的分析預測中，對CPI月度數據的變化趨勢和季節性進行了分析。[5]虞安和王忠采用引力模型和ARIMA模型對旅游人群進行了預測，對城市管理和旅游秩序的維護工作提供了意見和建議。[6]

本文將以汽車工業協會公布的汽車銷量月度數據為研究對象，根據月度數據同時具有長期趨勢效應、季節效應和隨機波動的特點，選取具有季節調整的ARIMA模型對汽車銷量進行預測。

2 模 型

3 建模過程

建模的過程主要分為以下四步：

第一步：序列平穩化。所研究的數據如果是非平穩的，則不滿足建模的條件，需要先對數據進行處理，在應用中差分x=xt-xt-1是常用的方法，差分后還需要通過ADF檢驗驗證序列是否已經平穩化。

第二步：模型識別。在這個過程中，繪制樣本的自相關函數圖（ACF）和偏自相關函數圖（PACF），然后觀察時間序列樣本的自相關系數和偏相關系數的特征確定ARMA模型的階數，模型階數的判斷標準如下：

第三步：模型擬合。在確定模型的階數后，需要對模型中的參數進行估計，這一步中常用的方法是最小二乘法，在實際的應用中，可通過統計軟件求得擬合值。

第四步：模型診斷。為保證模型的有效性，需要對模型進行殘差的白噪聲檢驗。殘差的LB統計量近似服從自由度為m的卡方分布，若統計量的P值大于顯著性水平，可認為殘差序列是純隨機序列，說明信息已被模型完全提取；反之則說明有些信息未能被提取，模型還需改進。為了保證模型的精簡性，還要對參數的顯著性進行檢驗，剔除不顯著為零的參數。

4 實例分析

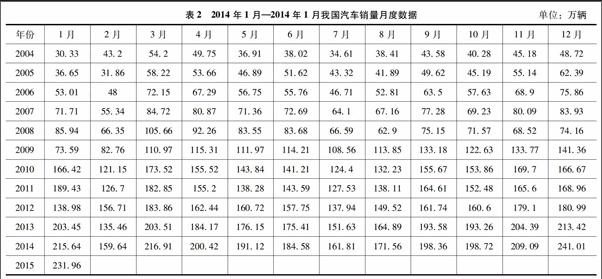
本文選取的研究數據為中國汽車工業協會公布的2004年1月—2015年1月全國汽車銷量月度數據，原始數據如表2所示。在建模過程中，將2004年1月—2014年3月的銷售數據用于構建模型，而將剩余數據將用于檢驗模型的預測效果。

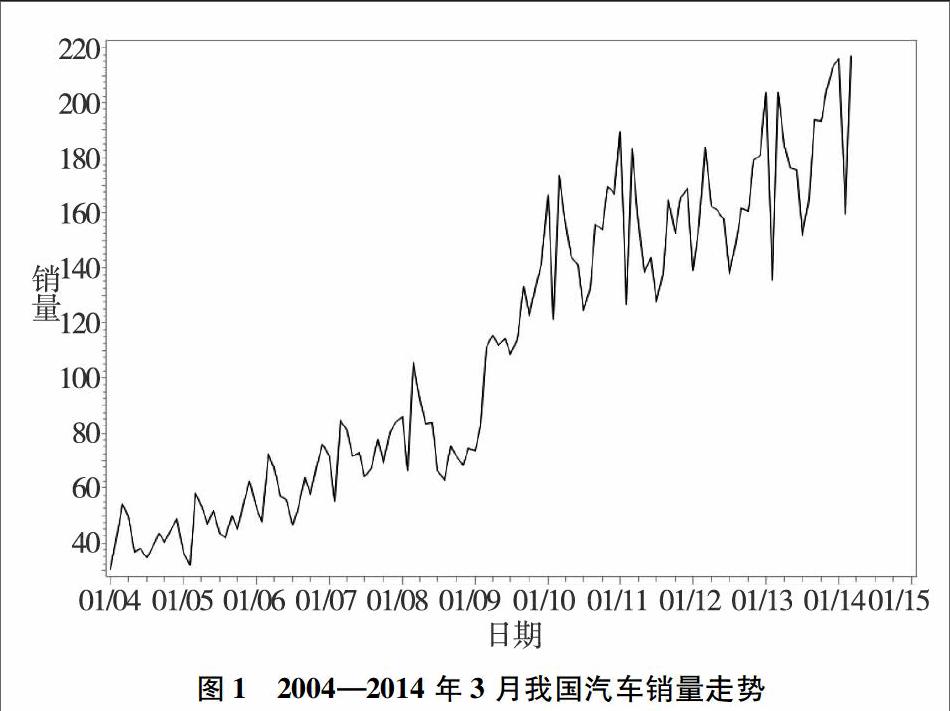
繪制汽車銷量走勢圖，如圖1所示。從圖中可以看出，我國的汽車銷量同時表現出波動趨勢和增長趨勢。由于春節假期因素的影響，每年2月都是全年的銷售淡季，與其他月相比較2月的汽車銷量大幅下滑。而從長期趨勢來看，汽車的銷量在逐年增長。

下一步對模型進行識別，首先繪制{zt}的自相關圖（ACF）和偏自相關圖（PACF），如圖3所示。圖像表明在延遲12階處，自相關系數和偏自相關系數都顯著非零；在延遲24階處，自相關系數完全落入了2倍標準差范圍以內，但是偏自相關系數仍然顯著非零。因此在季節自相關特征上，自相關系數截尾，而偏自相關系數拖尾。為了提取差分后序列的季節信息，可以使用ARMA（0，1）12模型。

然后再考慮模型的短期相關性，自相關系數和偏自相關系數在延遲2階后均快速衰減到2倍標準差之內，可以嘗試對p和q取不同的值，再根據SBC準則選出相對最優模型。在模型ARIMA（p，d，q）×（P，D，Q）12中，現在已知P=1，Q=1，以及d=1，D=1。在保持這四個參數不變的條件下，分別取p=1，2和q=0，1，2，SBC信息量的計算結果如表4所示。結果表明，當p=1，q=0時，SBC信息量相對最小。

5 結 論

在每月銷量的預測中，除了2014年12月的預測值與實際值偏差較大外，其余月份的預測偏差都控制在了3%以內，其中2014年6月、7月和10月的預測偏差更是控制在了1%以內，而預測值的平均絕對百分比誤差為MAPE=2.36，預測效果良好。

在年初由于春節假期的影響，汽車銷量往往較低，而在年末因汽車經銷商為完成銷售指標而開展各種促銷活動，汽車銷量出現高峰，汽車的銷售表現出明顯的季節性變化，選用具有季節調整的ARIMA模型是非常合理的。事實上在本例中SARIMA模型的預測偏差能夠控制在合理的范圍之內，該模型對汽車銷量預測活動具有良好的參考價值。

參考文獻：

[1]博克斯，詹金斯，格雷戈里，等.時間序列分析：預測與控制[M].4版.北京：機械工業出版社，2011.

[2]王燕.應用時間序列分析[M].3版.北京：中國人民大學出版社，2012.

[3]龔承剛，王夢，謝航.基于ARIMA模型的湖北省城鄉居民收入差距的預測[J].統計與決策，2014（15）：94-97.

[4]薛蓓蓓.基于ARIMA模型：全社會固定資產投資總額預測[J].統計與決策，2014（15）：141-143.

[5]張麗，牛惠芳.基于SARIMA模型的居民消費價格指數預測分析[J].數理統計與管理，2013（1）：1-6.

[6]虞安，王忠.基于ARIMA模型與時間序列的城市旅游傾向預測[J].統計與決策，2014（13）：86-89.