利用保羅機械阱探究囚禁粒子的動力學特性

馮　禹,習　爽, 何雨華,倪　晨,顧　牡,趙　敏

(同濟大學 物理科學與工程學院,上海 200092)

?

利用保羅機械阱探究囚禁粒子的動力學特性

馮禹,習爽, 何雨華,倪晨,顧牡,趙敏

(同濟大學 物理科學與工程學院,上海 200092)

摘要：在自制保羅機械阱上利用運動視頻分析軟件Logger Pro分析囚禁粒子的運動軌跡，形象地展現了囚禁粒子在勢阱中的不同運動狀態. 實驗測得失穩臨界值2q=0.989. 穩定條件下粒子被束縛在環形帶中，且q與躍動系數正相關. 粒子失穩按指數規律變化，在運動后期，摩擦力導致的失穩明顯顯現.

關鍵詞：保羅機械阱；非線性動力學；贗勢;Logger Pro

指導教師：何雨華(1959-)，男，上海人，同濟大學物理科學與工程學院高級實驗師，學士，主要從事物理實驗教學工作.

離子阱是研究量子理論重要的實驗裝置. 利用多極電勢構成三維勢阱，將離子穩定地囚禁在幾乎與外界隔離的空間幾何構型中的實驗方法，稱為離子囚禁技術[1]. 離子阱技術因其優良的特性和先進的功能，逐漸形成了一片新型廣闊的研究領域，如在量子信息[2-3]、量子計算邏輯門[4-5]、離子阱頻標[6]、大規模光譜測量[7-8]等研究中具有廣泛的應用. 囚禁粒子動力學特性及其穩定條件是離子阱研究的基礎，但是四極離子阱的結構復雜，不宜直觀地了解離子在其中的各種運動過程及離子的穩定性分析. 德國玻恩大學Wolfgang Paul教授利用可以旋轉的對稱馬鞍面裝置分析了離子在勢阱中的運動規律，故將此裝置命名為保羅機械阱[9]. 保羅機械阱的結構簡單，實驗現象清楚直觀，適合于進行單粒子在曲面運動規律的實驗探究和演示.

1實驗設計

1.1　運動的穩定條件

在與馬鞍面同步轉動的參考系中,容易得到馬鞍面中重力勢場為

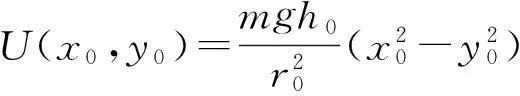
(1)

其中h0為鞍點到馬鞍面最高點的垂直距離,r0為對稱馬鞍面的投影面半徑，x0和y0為旋轉參考系中的坐標. 通過對(1)式乘以旋轉矩陣可以得到在實驗室坐標系下的勢能方程為

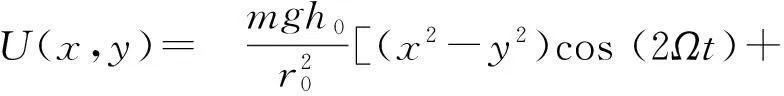
2xysin (2Ωt)],

(2)

其中Ω為馬鞍面旋轉的角頻率.

對實驗室參考系中的勢場求負梯度，建立粒子運動的動力學方程組，可解出粒子的軌跡方程為[10]

z(τ)=(Ae+β+τ+Be-β+τ+Ce+β-τ+De-β-τ)eiτ,

(3)

其中τ為運動時間與旋轉頻率的乘積，β由馬鞍面的形狀與旋轉速度決定：

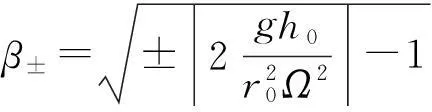
(4)

τ=tΩ.

(5)

由(4)式可知，β為冪指數，要使上述解不發散，則β必須為純虛數，方便起見令

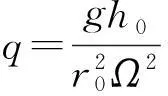
(6)

要使所有β±為純虛數，則q應滿足

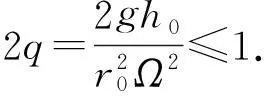
(7)

當2q≥1時，冪指數β為實數，此時解是發散的;當2q<1時，冪指數β為虛數，此時粒子的運動方程為穩定的周期運動. 在實驗中可以通過調節轉速來改變q:當馬鞍面的轉速增大時，2q的值減小，則粒子更容易處于穩定狀態. 此外粒子的穩定條件與馬鞍形狀有關，投影面半徑越大，馬鞍半徑越小，更容易實現粒子俘獲.

1.2　動力學方程的定解條件

通過對(3)式求導,可以得到4個線性無關的方程組:

A+B+C+D=z0,

(8)

iμ+(A-B)+iμ-(C-D)=v0-iz0,

(9)

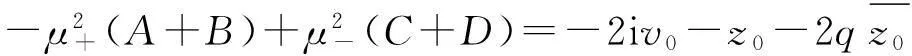
(10)

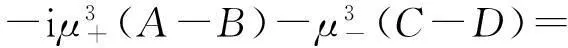
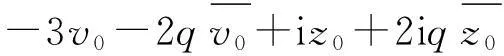
(11)

只要知道z0,v0和q,便可以求解線性方程組,從而確定參量A，B，C，D,得出囚禁粒子的運動軌跡. 當初始條件為z0=1.00 cm,v0=0.01 m/s,q=0.05時,計算粒子運動軌跡,如圖1所示.

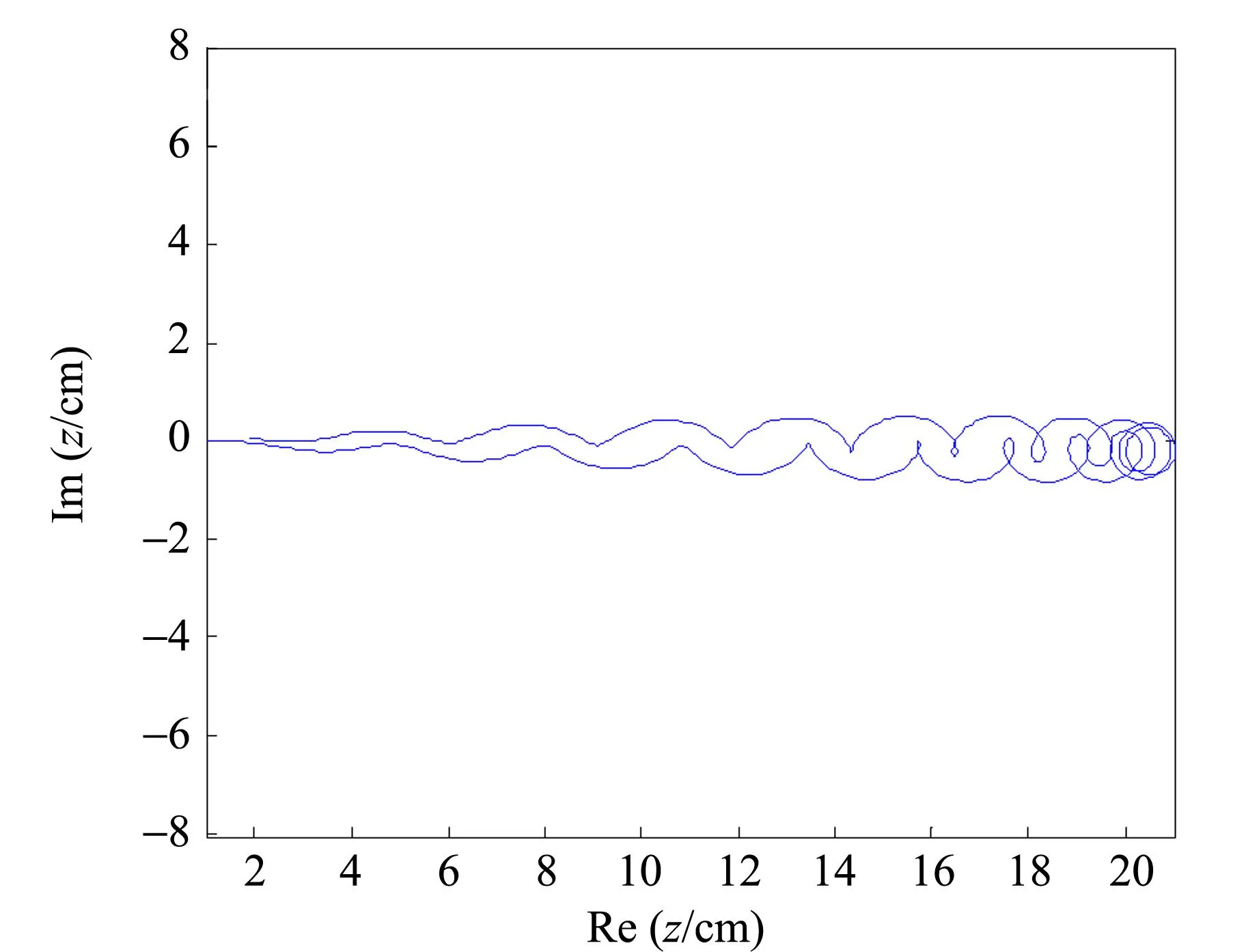
(a)短周期

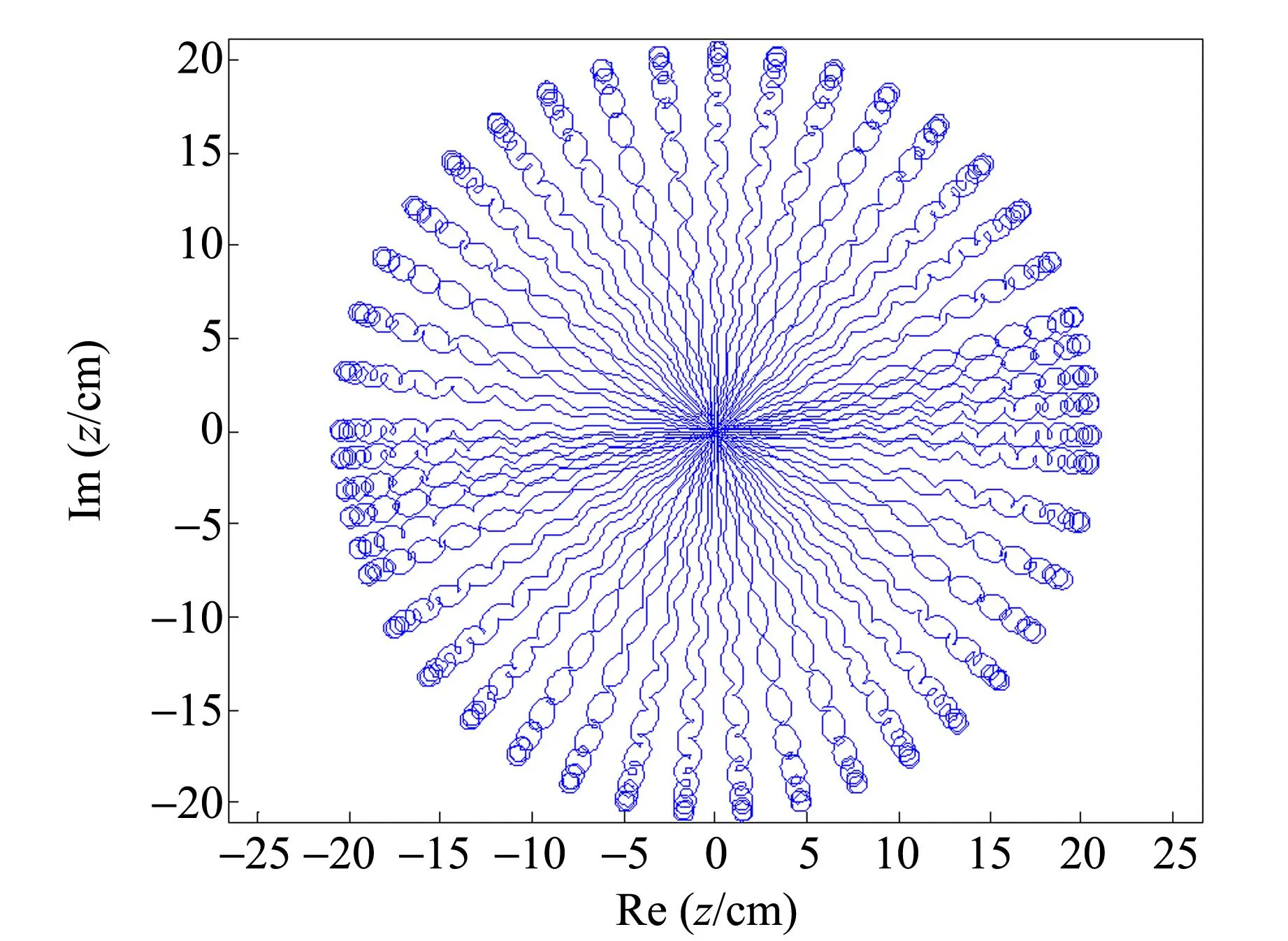
(b)長周期圖1　不同時間周期下粒子的運動軌跡

不難發現,計算結果與四極離子阱中囚禁粒子的運動軌跡相似[11]. 從圖像中可以看到,囚禁在勢阱中的粒子一方面在進行頻率較高的躍動,同時又存在對稱于鞍點周期較長的振動.不僅如此,粒子的運動軌跡在平行于馬鞍面內以周期為q2Ω轉動. 這樣根據運動形式將囚禁粒子的運動分為高階微振動、諧振運動和長周期轉動. 當馬鞍面的轉速較高時，高階微振動振幅較小，此時可近似視為粒子在諧振勢場中的運動. 當馬鞍的轉速較低時，高階微振動不可忽略，此時粒子的運動軌跡為上述3種運動的合成. 接下來將通過實驗分析在穩定條件下囚禁粒子的運動軌跡.

2實驗開發

2.1　穩定條件的驗證

實驗裝置如圖2所示. 馬鞍面固定在旋轉臺上,通過皮帶傳動裝置及馬達與電源相連接,旋轉臺的轉速可通過改變負載兩端的電壓進行調節.旋轉周期由光電門讀出.馬鞍面的參量為r0=20.95 cm,h0=5.29 cm,負載電壓可調范圍為0~10 V,旋轉臺可調控最高轉速為16 r/s. 實驗中,通過改變馬鞍面的轉速來改變系統的q值.當轉速穩定時將小球垂直放入鞍點,并利用計時器記錄小球放入至飛出馬鞍面的時間.

圖2　實驗裝置圖

為了減小放入時由于初始條件不同引起的偶然誤差,對每組確定的轉速重復多次實驗,取小球的最長穩定時間與q值作圖. 實驗結果見圖3，圖中虛線代表理論臨界值2q=1. 實驗發現在臨界值兩側,小球的運動發生了失穩,實驗測得的失穩臨界值為2q=0.989,相對偏差為1.1%. 理論模擬中,可明顯發現粒子的運動軌跡由封閉的曲線變為發散. 圖4分別給出了q=0.499 9與q=0.500 1的粒子運動軌跡.

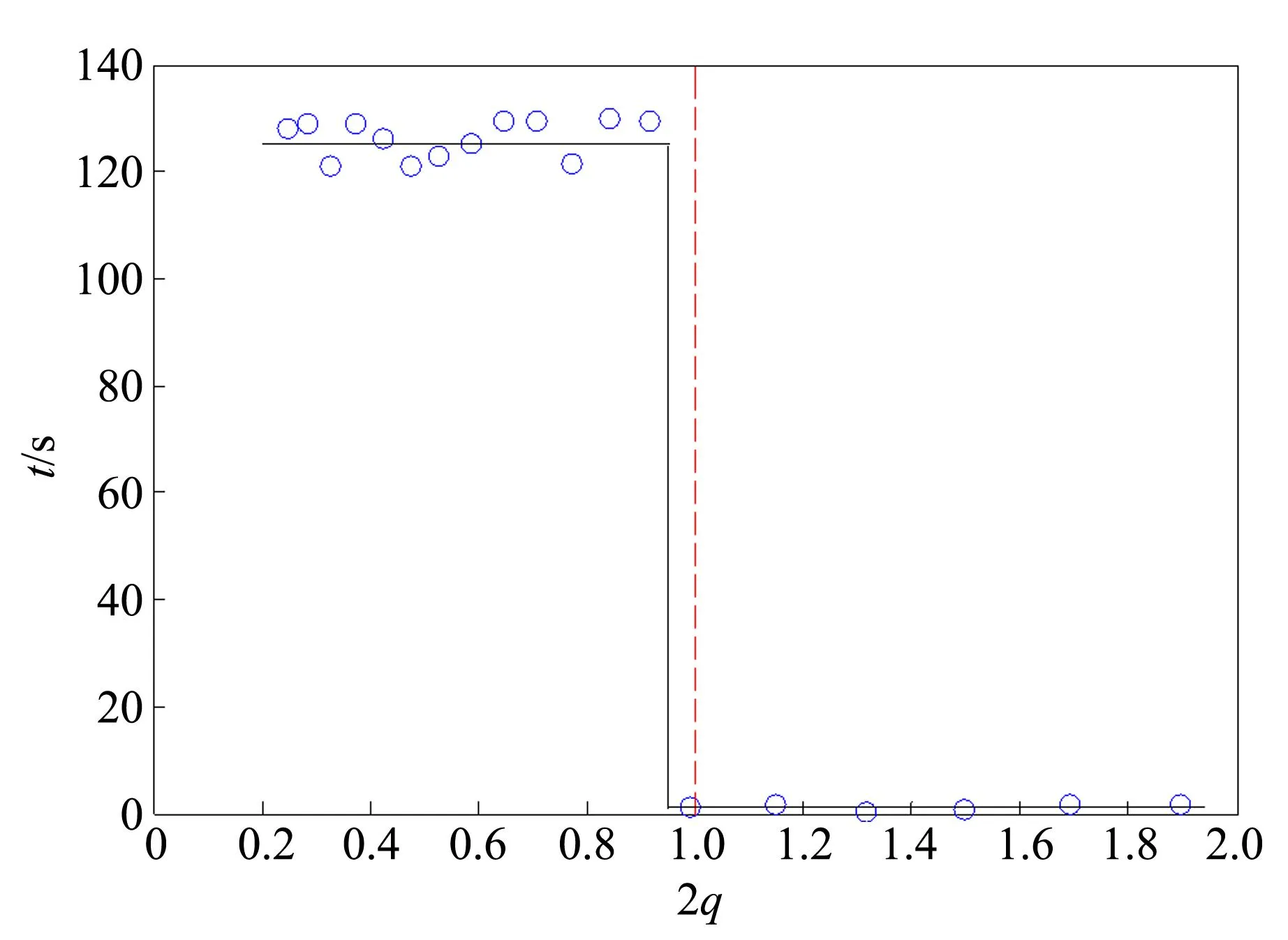
圖3　粒子穩定時間的實驗驗證圖

(a)q=4.999 9

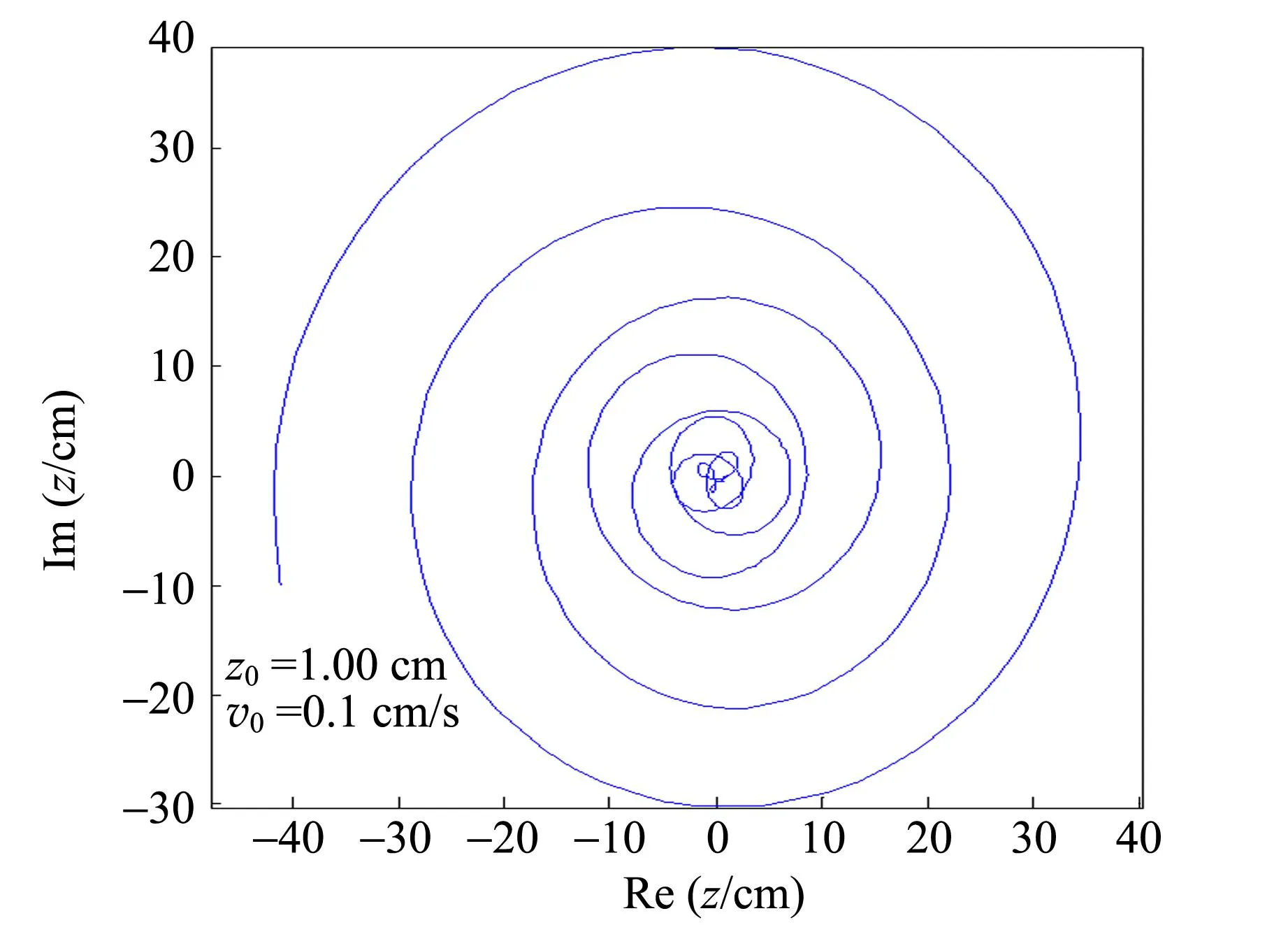
(b)q=0.500 1圖4　臨界條件下粒子運動軌跡圖

同時,我們發現實驗中即使滿足2q<1,粒子并不能一直處于穩定狀態,這是由于摩擦力引起的失穩現象.

2.2　穩定條件下粒子運動軌跡的實驗驗證

我們不僅僅滿足于確定粒子在何種情況下會保持穩定,更希望知道粒子在穩定條件下是如何運動的,前面已經給出了粒子的運動方程,現在將用實驗的方法得到粒子的運動軌跡.

實驗中用攝像機記錄小球的運動軌跡,利用Logger Pro[12]軟件將粒子運動的視頻導入分析,可以得到粒子的初始位置、初始速度以及穩定條件下的運動軌跡. 在相同條件下進行計算模擬,初始條件為z0=0.14 cm,v0=0.03 cm/s,r0=20.95 cm,h0=5.29 cm,對比如圖5所示.

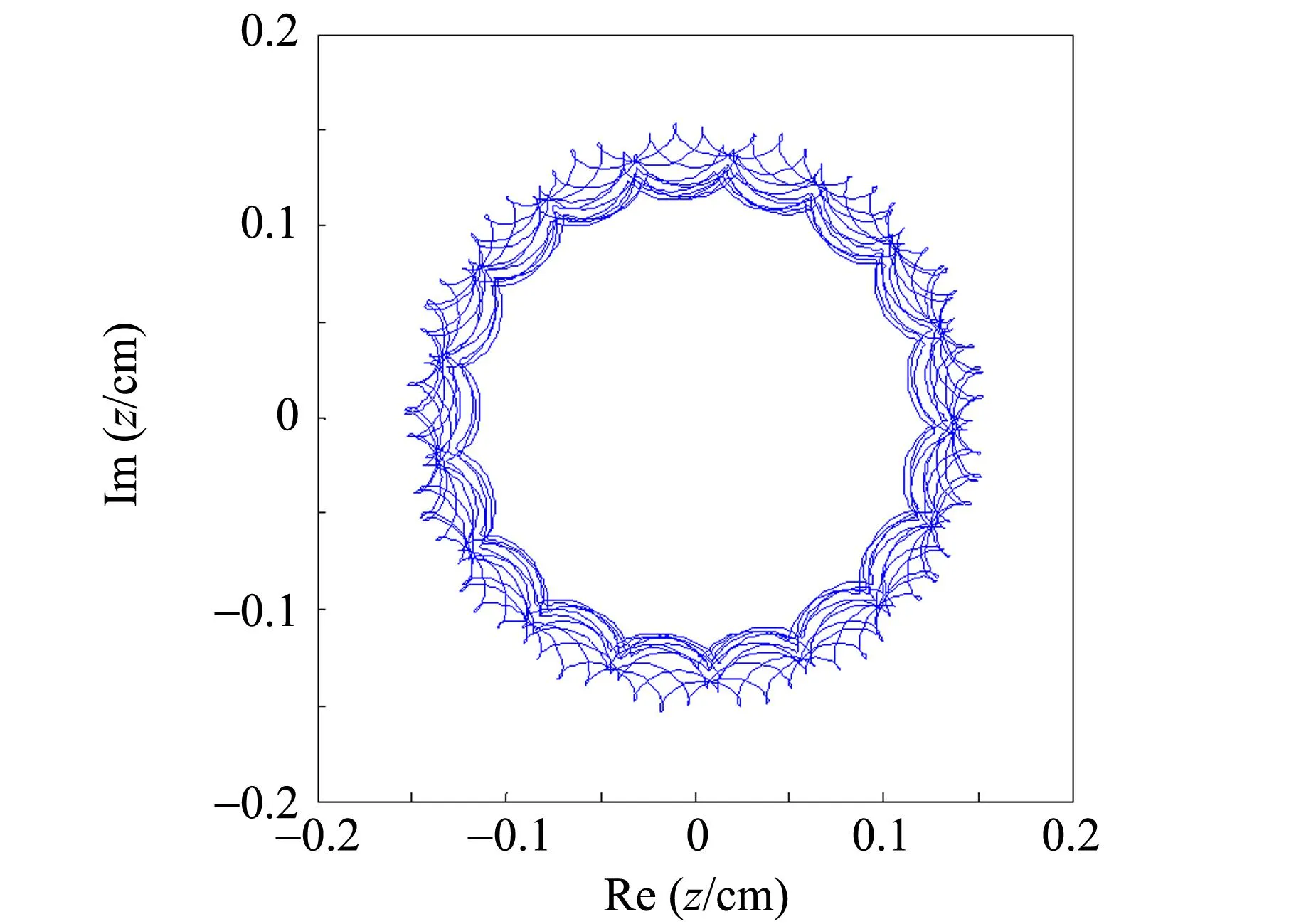
(a)模擬軌跡

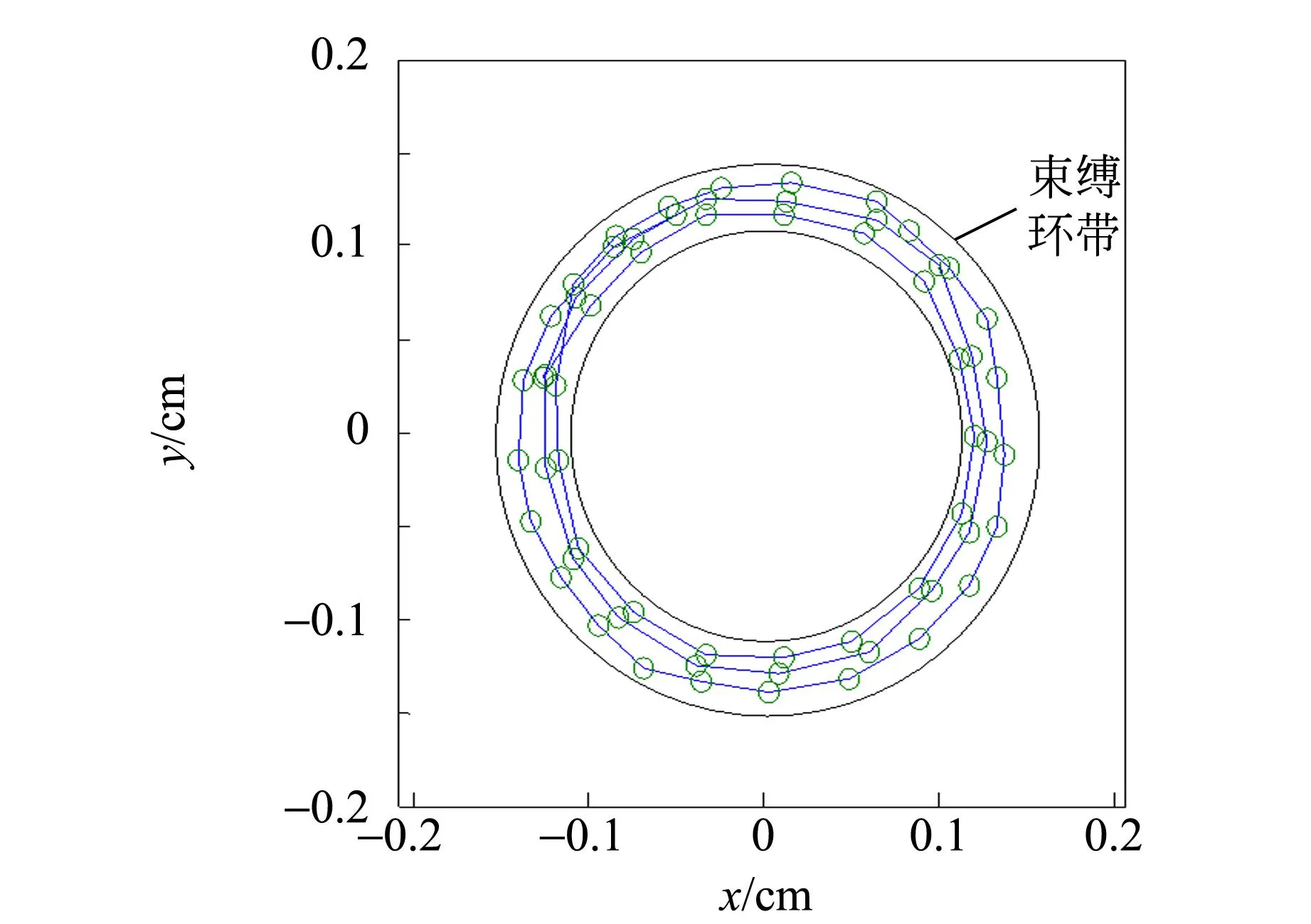
(b)實際軌跡圖5　穩定條件下粒子運動軌跡的實驗對比圖

通過圖5的對比,可發現粒子軌跡被束縛在環形內,理論軌跡中該環形的內徑與外徑與實際情況符合較好. 但是環形的束縛帶只是由初始條件決定的一種特殊的囚禁模式.

2.3　粒子不同時間周期下運動的分析與討論

在保羅機械阱中,粒子做諧振運動的運動方程為[13]

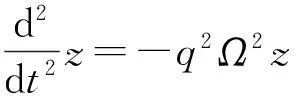
(12)

即粒子在二維平面上做角頻率為qΩ的簡單諧振子運動,其軌跡為頻率比為1∶1的李薩如圖形,初始相位差由粒子的初始條件決定.

實驗中發現,當q?1時,粒子的高階微振動便可以忽略. 定義在環形囚禁帶的情況下,粒子的躍動系數為環帶寬度與粒子高階微振動的模長的比值,即

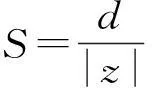
(13)

其中d為環帶寬度,可以預見,q減小時,S也隨之減小. 圖6給出了不同q下躍動系數的變化規律,模擬的初始條件為z0=0.10 cm,v0=0.

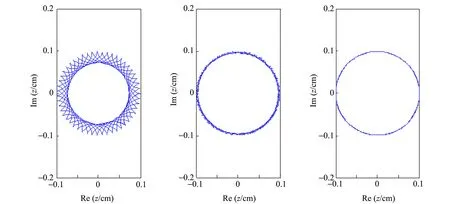
(a)q=0.45　　　　　　　　　　(b)q=0.045　　　　　　　　　(c)q=0.004 5圖6　不同q值對高階微振動躍動系數的影響

從圖6可看出,q與S呈正相關關系,當q→0時,粒子的高階微振動也隨之消失. 但是粒子的運動不僅僅是簡單囚禁在圓環內,這由粒子的諧振運動所決定. 粒子的諧振運動軌跡為頻率比為1∶1的李薩如圖形,其運動軌跡方程為

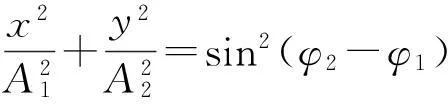
(14)

在復平面內,粒子運動的相位差由粒子初始釋放位置決定：

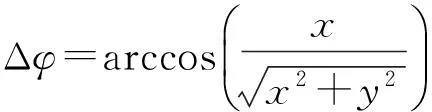
(15)

不同的相位差決定了粒子的諧振運動為圓、橢圓以及直線. 但是在實驗中發現,即使在很小q下,粒子的軌跡依然不是穩定的李薩如圖形,而是會有以鞍點為中心、頻率為q2Ω的轉動,這構成了粒子的長周期轉動. 在高速的馬鞍轉動下,粒子的高階微振動退化,在短時間內,粒子的長周期轉動無法顯現,此時粒子的軌跡主要表現為李薩如圖形. 下面分別給出了初相位差為零的囚禁粒子諧振運動軌跡和長時間下的長周期轉動軌跡，如圖7所示. 文獻[13]中囚禁粒子運動的二維投影與此相同.模擬的初始條件為z0=0.1+0.1i,v0=0,q=0.01.

一般情況下,粒子的諧振運動軌跡為橢圓,高階微振動躍動系數也不為零,加之整個軌跡圍繞鞍點轉動,這3種周期運動的疊加,便構成了圖1所示的一般運動軌跡.

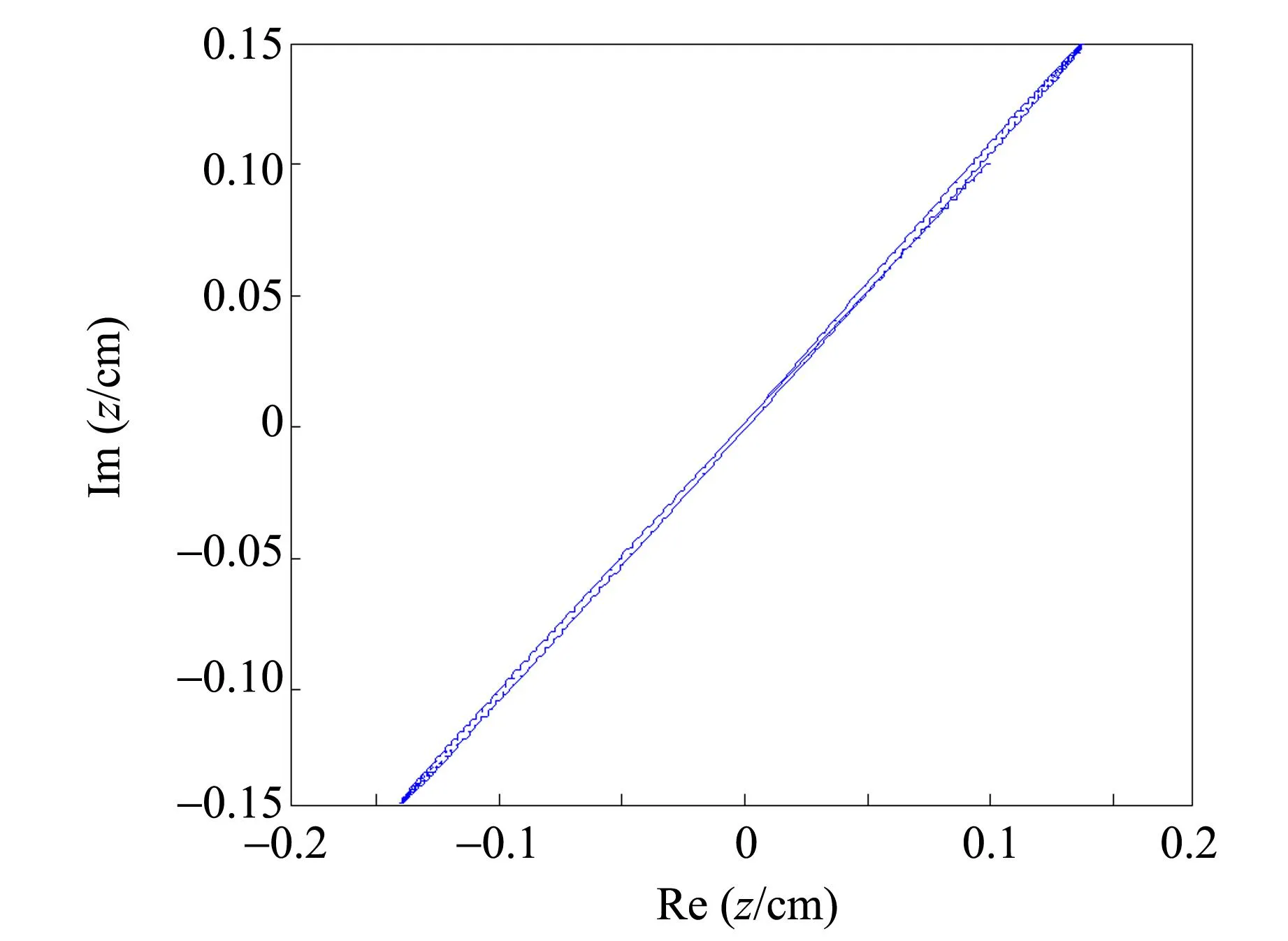
(a)諧振運動

(b)長周期轉動圖7　囚禁粒子的諧振運動和長周期轉動

2.4　摩擦力對囚禁粒子運動的影響

μ為小球與馬鞍面之間的摩擦系數,則在該體系中摩擦力的形式為

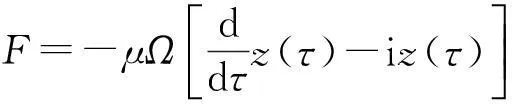
(16)

加入摩擦力項的運動軌跡為

z(τ)=[Ae(+β++ε)τ+Be(-β++ε)τ+

Ce(+β-+ε)τ+De(-β-+ε)τ]eiτ，

(17)

其中

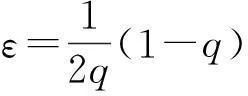
(18)

(18)式的值總為實數,因此在足夠長的時間,總會引起解的發散,這也是實驗中粒子無法一直保持穩定的原因.

利用Logger Pro軟件將臨近失穩狀態的粒子運動視頻導入分析,得到其運動軌跡,并在相同條件下進行計算模擬,初始條件為z0=1.02 cm,v0=0.03 cm/s，結果如圖8所示.

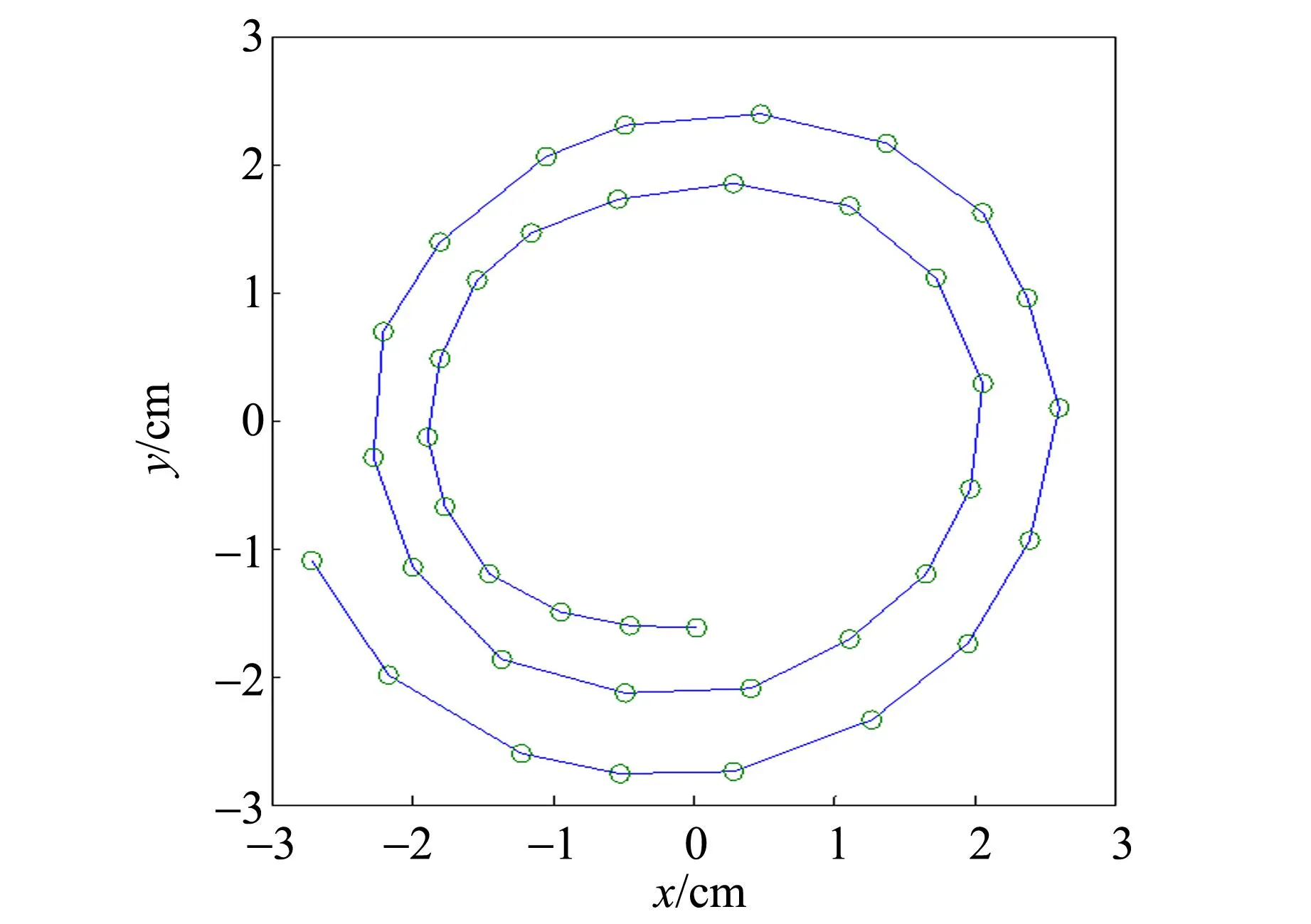
(b)臨近失穩條件下的粒子運動軌跡圖8　臨近失穩階段粒子的運動軌跡與計算模擬對比

由于粒子的失穩是按指數規律變化的,因此實驗中常常看到的現象是穩定運動的小球突然快速脫離馬鞍,而其在前期運動的軌跡更接近無摩擦力計算模擬下的軌跡,只有在運動的后期,摩擦力導致的失穩才會明顯地表現出來.

3結束語

保羅機械阱形象直觀地展示了四級離子阱俘獲粒子的概念和原理，將抽象的物理模型，以生動且有趣的實驗形式呈現. 實驗中通過運動視頻分析軟件Logger Pro捕獲粒子運動軌跡，為學生提供了處理動力學問題的新方法和手段. 借助于Matlab使枯燥的理論推導可視化，將數學推導與物理分析緊密結合，有助于培養學生解決一般性物理問題的綜合能力. 實驗中宏觀與微觀之間的類比，能夠很好地激發學生的探究興趣，從而實現創新思維的培養，也為教師提供了微觀現象教學與演示的新思路.

參考文獻：

[1]Hasegawa T, Bollinger J J. Rotating-radio-frequency ion traps [J]. Physical Review A, 2005,72(4):043403.

[2]Steane A, Roos C F, Stevens D, et al. Speed of ion-trap quantum-information processors [J]. Physical Review A, 2000,62(4):042305.

[3]David S, Brochard J, Steane A M. Simple experimental methods for trapped-ion quantum processors [J]. Physical Review A, 1998,58(4):2750.

[4]Barenco A, Deutsch D, Ekert A, et al. Conditional quantum dynamics and logic gates [J]. Physical Review Letters, 1995,74(20):4083.

[5]Zhang X D, Zhang Q H, Wang Z D. Physical implementation of holonomic quantum computation in decoherence-free subspaces with trapped ions [J]. Physical Review Letters, 2006,74(3):034302.

[6]羅學立,朱熙文. 離子囚禁技術與量子計量基準的新進展[J]. 物理,1996,25(9):539-543.

[7]Kreuter A, Becher C, Lancaster G P T, et al. Experimental and theoretical study of the 3d2D-level lifetimes of40Ca+[J]. Physical Review A, 2005,71(3):032504.

[8]Barwood G P, Huang G, Klein H A, et al. Subkilohertz comparison of the single-ion optical-clock2S1/2-2D5/2transition in two88Sr+traps [J]. Physical Review A, 1999,59(5):R3178.

[9]Paul W. Electromagnetic traps for charged and neutral particles [J]. Reviews of Modern Physics,1990,62(3):531-540.

[10]Thompson R I, Harmon T J, Ball M G. The rotating-saddle trap: a mechanical analogy to RF-electric-quadrupole ion trapping [J]. Canadian Journal of Physics, 2002,80(12):1433-1448.

[11]March R E. An introduction to quadrupole ion trap mass spectrometry [J]. Journal of Mass Spectrometry, 1997,32(4):351-369.

[12]Vernier software & Technology [EB/ON]. http://www.vernier.com.

[13]Forbes M W, Shari M, Croley T, et al. Simulation of ion trajectories in a quadrupole ion trap: a comparison of three simulation programs [J]. Journal of Mass Spectrometry, 1999,34(12):1219-1239.

[責任編輯：任德香]

Study on the dynamics of trapped particles

using the rotating-saddle trap

FENG Yu, XI Shuang, HE Yu-hua, NI Chen, GU Mu, ZHAO Min

(School of Physics Science and Engineering, Tongji University, Shanghai 200092, China)

Abstract:Using the motion video analysis software Logger Pro, the motion of particles in self-made rotating-saddle trap was analyzed, and different motion states were shown. The critical value of neutral stability was 2q=0.989. The particles were bound in girdle in the stable state, andqand vigor coefficient were positively correlated. The destabilization of the particle appeared to obey an exponential rule, and in the late phase of the motion, obvious destabilization caused by friction force occurred.

Key words:rotating-saddle trap; nonlinear dynamics; pseudopotential; Logger Pro

作者簡介：馮禹(1995-)，男，甘肅慶陽人，同濟大學物理科學與工程學院2013級本科生.

收稿日期：2015-11-02；修改日期：2015-12-23

中圖分類號：O317

文獻標識碼：A

文章編號：1005-4642(2016)02-0001-06