頻域內換熱管振動載荷識別

田 雷, 吳遠峰, 張正習

(國核工程有限公司,上海 201100)

頻域內換熱管振動載荷識別

田 雷, 吳遠峰, 張正習

(國核工程有限公司,上海 201100)

常用的載荷識別可以通過時域和頻域進行解決.主要在頻域內進行換熱管載荷的識別,由于是初次進行嘗試,因此選取單根的、線性結構的換熱管進行研究,通過理論的推導和有限元模擬進行了載荷的成功識別.

換熱管; 載荷識別; 頻域

蒸汽發生器系統是核電站一、二回路的樞紐,它的主要作用是將一回路冷卻劑中的熱量傳遞給二回路給水,使之產生蒸汽來驅動汽輪發電機組發電.AP1000核電機組中蒸汽發生器基本參數主要有:設計溫度(二次側)315.5℃;設計壓力(二次側)8.274 MPa;每個蒸汽發生器流量為3.40×106 kg·h-1;每臺換熱器中含有10025根φ17.48 mm×1.01 mm的U型換熱管,其中U型管最大的彎曲半徑為1 887.22 mm,最小彎曲半徑為82.55 mm.換熱管工作環境惡劣,一二次側均為高溫高壓快速流動的兩相流體,長年的運行對管壁不斷沖刷會造成磨損腐蝕.這種因為流體流動而使換熱管損壞的現象叫流體誘導振動[1].這些金屬的局部腐蝕對蒸汽發生器的換熱管危害很大,容易造成換熱管在運行過程中的失效,且具有難以預測的特點.

流體誘導管束的振動以及核燃料棒的振動在工程上是一個非常重要的問題.由湍流以及其他可能的流彈性現象產生的激勵會導致換熱管因材料疲勞而造成提前失效,或者因受到振動沖擊而有所磨損.因此諸多學者[2-4]提出了很多預測方法和計算機程序式,對實際工程中的多支撐管束和流動分布進行管束的響應以及磨損的分析,并且這些方法和計算機程序得到的結果和驗證的試驗結果[5-8]有著良好的一致性.本文主要是在頻域內進行換熱管振動載荷的求解和識別,模型暫時主要是針對簡單的單根換熱管進行嘗試.

1 頻域內的載荷識別

換熱管振動的響應反問題即是由換熱管振動的響應和系統參數數據來確定換熱管所受的載荷的問題.按照對響應處理方式,可分為時域法和頻域法.時域和頻率內反問題求解方法的聯系和區別如圖1所示.

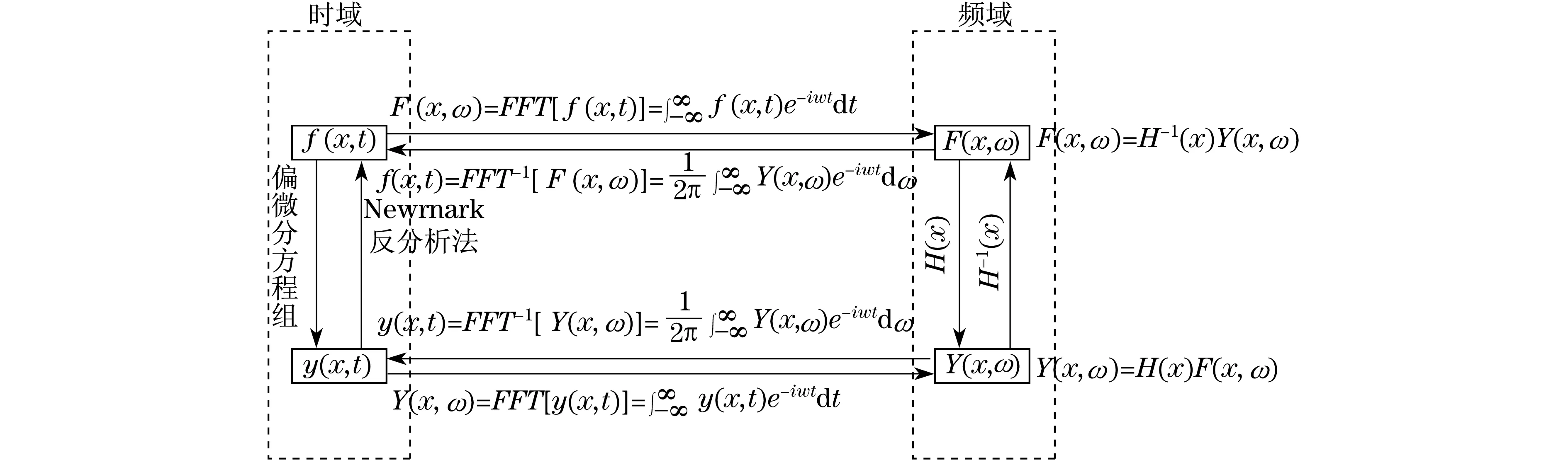
圖1 激勵載荷識別的過程Fig.1 Load identification process

Antunes[9-10]等在時域內將激勵載荷的識別問題轉變成一個求解響應反卷積過程的基本問題,當轉換到頻域中進行載荷識別時,則會更實用.利用頻域法進行載荷識別會用到快速傅里葉變換和逆變換技術.

頻域法進行載荷識別的過程大致如下:假設在點xE處存在激勵F(xE,t),在測量點xR可得時域的響應信號為y(xR,t),那么識別過程大致可為

(1)

式中：H(xE,xR,ω)為xE,xR之間的傳遞函數,對應不同測量信號有不同的傳遞函數,具體有位移傳遞函數、速度傳遞函數和加速度傳遞函數.

位移傳遞函數為

(2)

對應的速度和加速度傳遞函數依次為

(3)

(4)

整個過程的載荷識別是需要多個激勵和測量點才能更好實現.在識別的過程中,約束處和接觸面的相互作用載荷都是可以獲得.式(1)看似簡單,實質上識別過程非常復雜,識別結果的準確性很大程度上取決于環境噪音和模型準確性.

2 算例分析

2.1 模型說明

本文主要利用簡化梁模型進行計算,利用HyperWorks軟件進行有限元分析,如圖2所示.

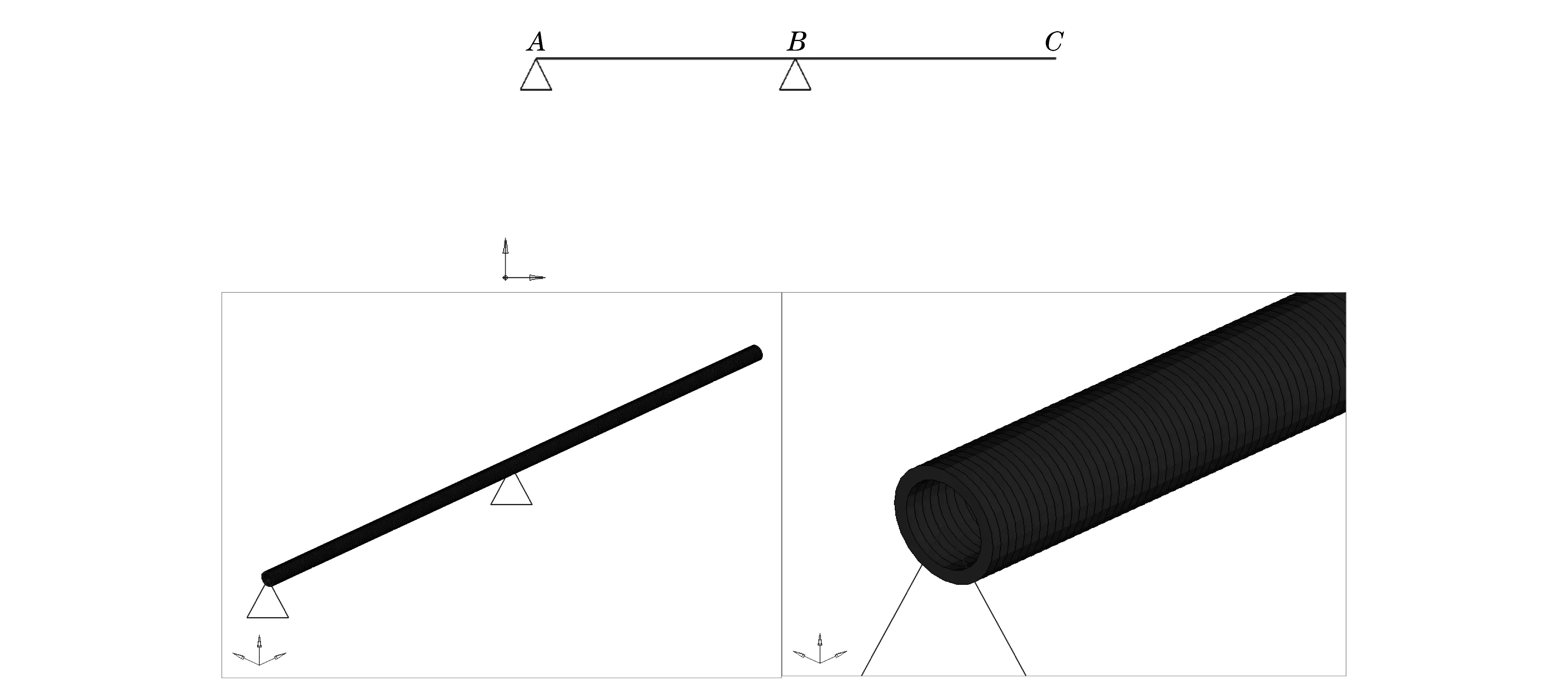
圖2 模型說明Fig.2 Model diagram

為了降低頻率,將約束修改為一端固支.換熱管外徑25 mm,管厚3 mm,AC長1 000 mm,AB長500 mm,在模型左端,也就是A點采用全約束固支,材料彈性模量E,泊松比0.31,密度13.3×10-9t·mm-3.其中B點為激勵輸入點,C點為數據輸出點,也就是響應測量點,節點號為502.有限元模型為1D梁單元,單元總數為500.分析過程中輸入0.03的臨界阻尼或者對應0.06的結構阻尼.

這種模式也可稱為常規慕課模式，對社會大眾免費開放所有課程資源，實現精英教育大眾化。通過線上定期發布慕課視頻，并組織各種線上學習活動，按照預定授課計劃完成課程的教學。隨著學習者人數增多，需要按照一定比例配備相應數目的課程助教。目前愛課程等網站發布的在線開放課程均屬于該類模式。這種作法的優點是受眾面廣，可以實現優質教育資源的大眾化共享應用，但是這種模式的教學過程管理并不理想，多數學員注冊開始學習后不能堅持完成學習，教師對眾多學習者的學習支持也不夠，因此教學效果也沒有保證。這種模式的教學效果很大程度上依賴于課程本身的教學質量和學習者的學習興趣及自覺性，這種常規慕課的教學模式很難實現可持續發展。

2.2 試驗原始激勵數據

作為對比的原始激勵,也就是識別載荷,選取兩周期的正弦信號15 sin 20t,幅值1.5 mm,總共1 024個數值點,橫軸由0～0.628319,信號見圖3.為了結構安全的可控性,暫時取信號為位移激勵,單位為mm.

2.3 結構瞬態響應分析數據

在瞬態分析時,施加速度或者加速度激勵的過程中,難以找到合適的激勵信號.如果信號不合適,則會導致結構的破壞和不穩定,但輸入位移激勵信號時,通過控制最大和最小位移則可以保證結構的安全性和穩定性.

從圖3所示的位移激勵信號可以看出,整個周期的位移激勵絕對值最大為1.5 mm.經過試算,在此模型中間施加強制位移1.5 mm時,結構是安全和穩定的.利用模態法進行瞬態分析,將圖3所示的位移激勵信號從B點輸入,信號為xz平面中的z方向,獲取C點的z方向位移時間響應.

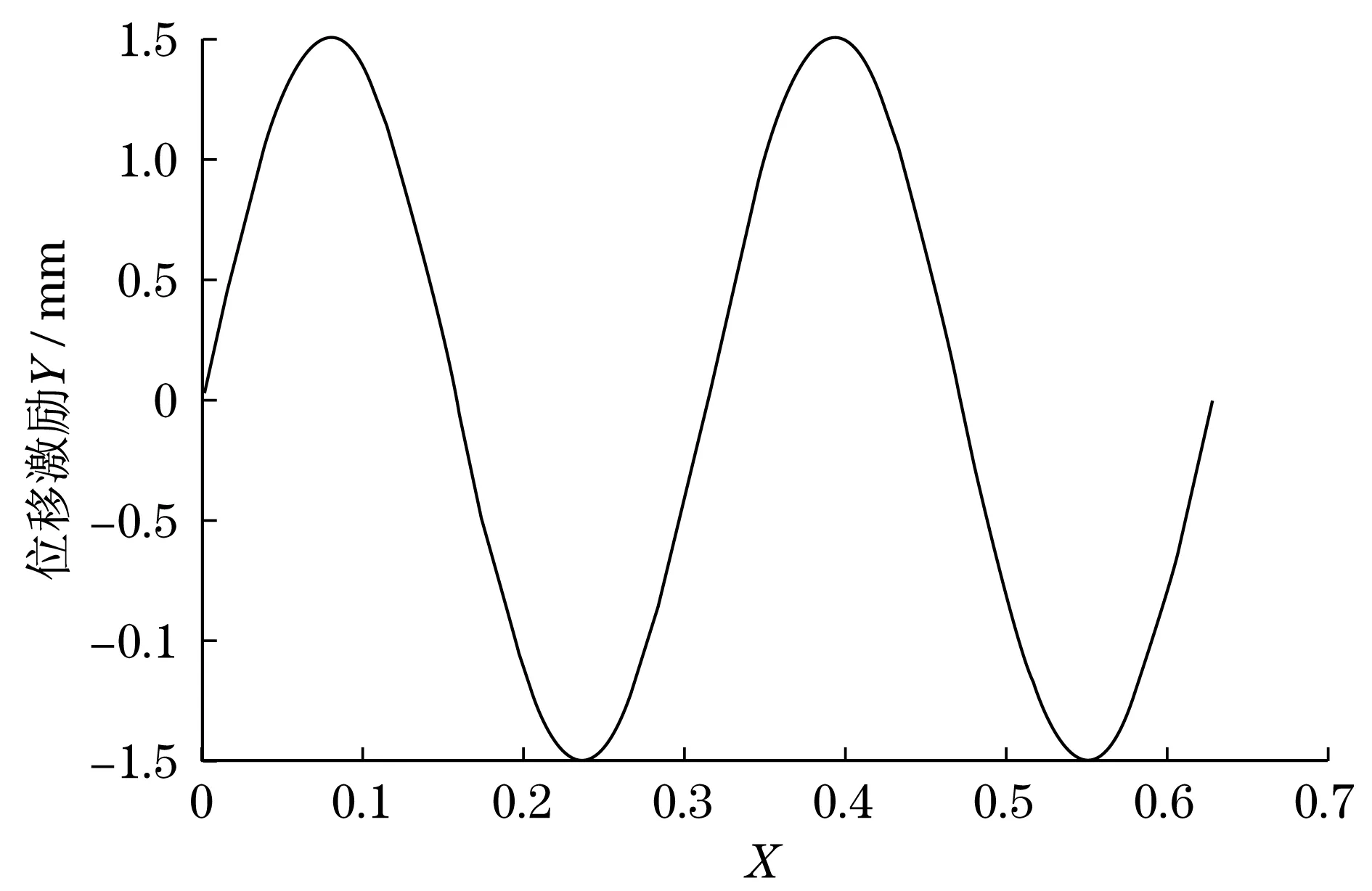
圖3 原始位移激勵信號Fig.3 Original displacement

信號輸出同樣取1 024個點,時間步長為0.002 5 s,輸出時間0～2.557 5 s.數據輸出見圖4.可知最大位移在時間0.075 s處,位移為5.641 89 mm,整個過程在0.655 s后進入自然衰減.

2.4 快速傅里葉變換

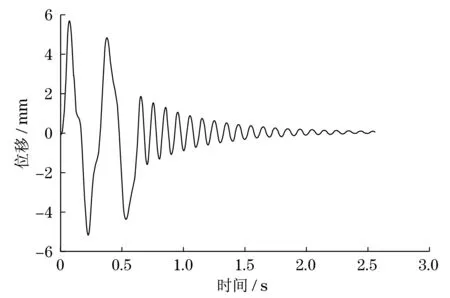
圖4 瞬態位移響應數據Fig.4 Transient displacement response date

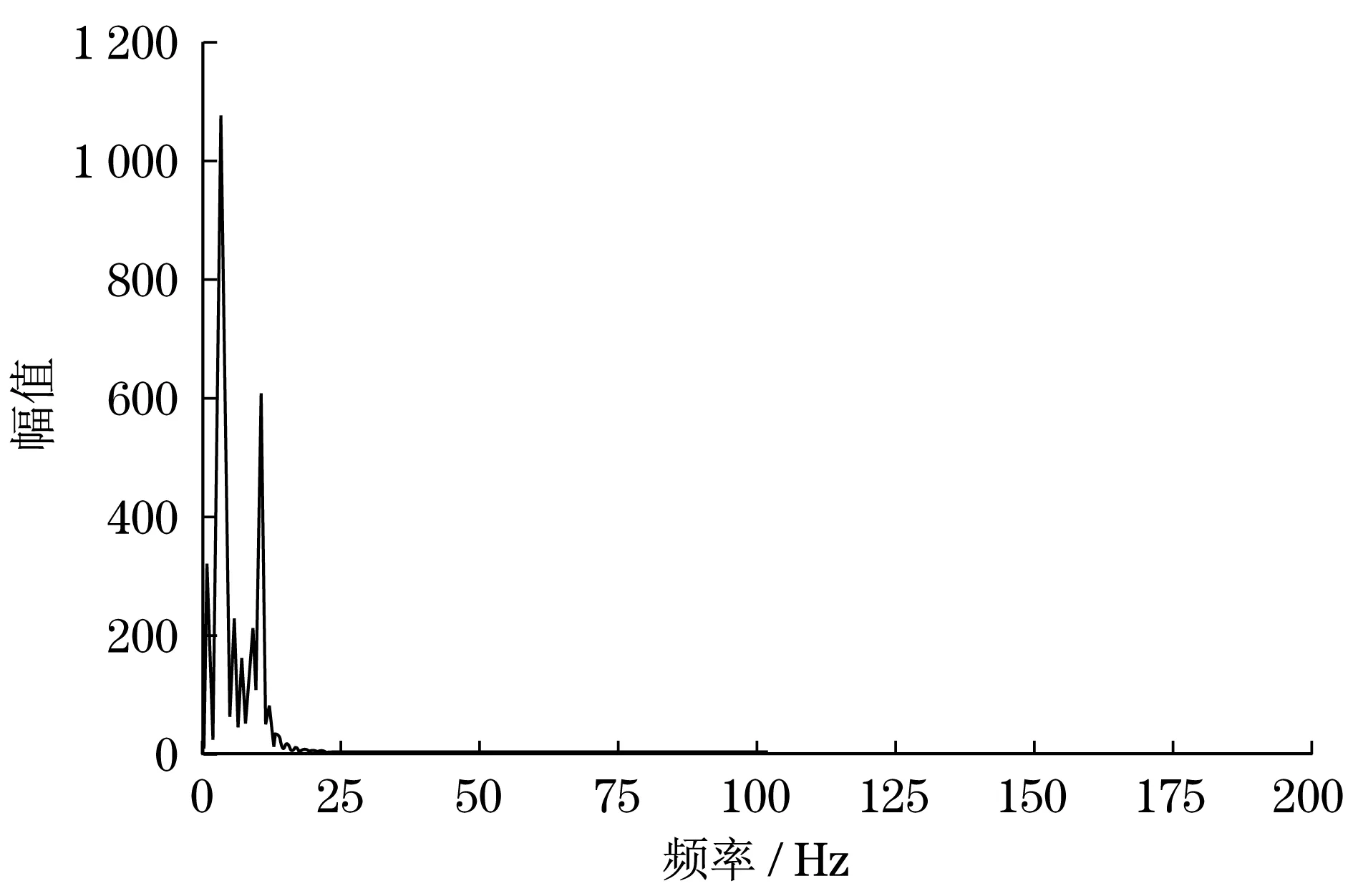
圖5 幅值單邊譜圖Fig.5 Amplitude one-side

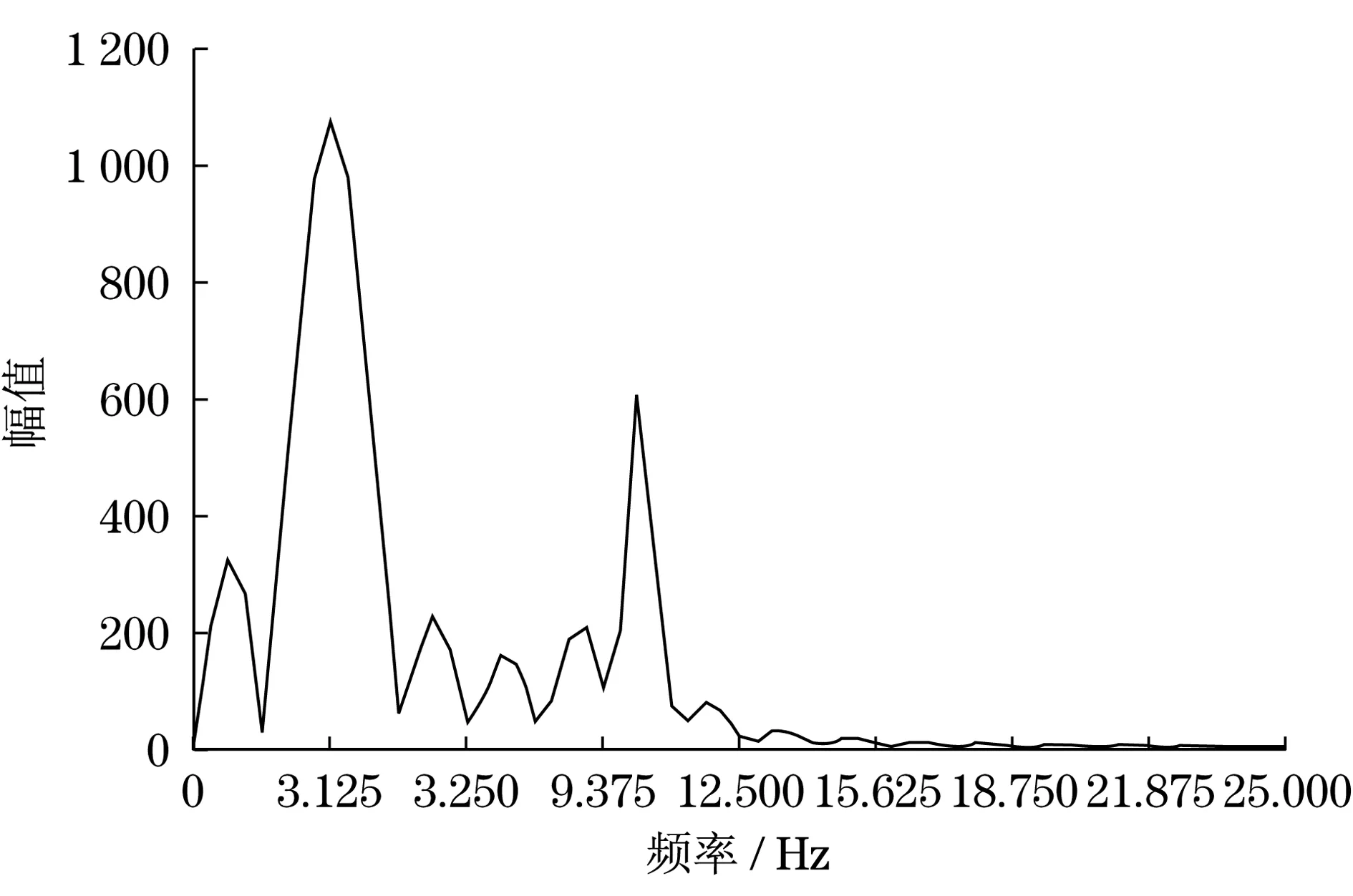
圖6 單邊譜局部放大圖Fig.6 Amplitude one-side local

通過圖6單邊譜局部放大圖可知道,兩個幅值的最大點處的頻率依次為3.125 Hz和10.156 3 Hz.圖7是相位的單邊譜曲線.

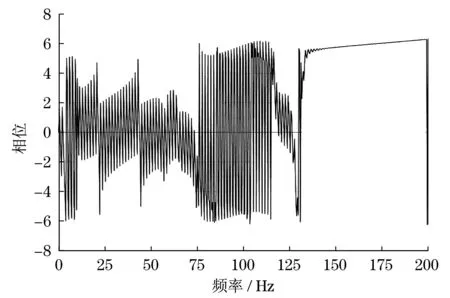
圖7 相位單邊譜Fig.7 Phase one-side

2.5 結構頻響傳遞函數及轉換數據

激勵、響應與傳遞函數的關系為

(5)

從式(5)可知,在頻域中的傳遞函數,只要輸入z方向單位1的激勵,便可以獲得對應的傳遞函數.依然是圖2所示的有限元模型,在激勵點B處輸入單位1 mm的位移激勵,輸入頻率范圍為0～1 000 Hz,模態的疊加范為0～1 000 Hz,輸入0.06的結構阻尼,輸出位移幅值及對應的相位,從0 Hz開始,增量為0.391 Hz,輸出1024步.

在0～1 000 Hz的范圍內,可以獲得20階模態頻率,前六階數值具體見表1.

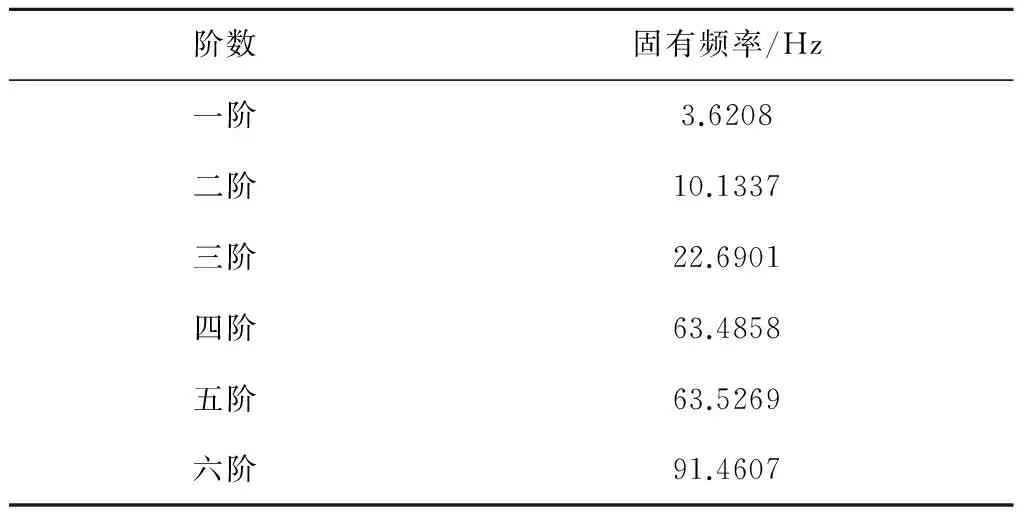
表1 結構前六階頻率

可得z方向的位移頻率輸出曲線,如圖8所示,也即是位移頻響傳遞函數.將xy軸取對數,可得對應的伯德圖,如圖9.相位圖見圖10.

2.6 快速傅里葉逆變換及載荷識別

已得到原始響應在頻域里的幅值和相位兩條曲線,同時也有在頻域里的位移傳遞函數的幅值和相位的曲線,因此將數據提取至MATLAB中進行傅里葉快速轉換處理.可以得激勵點B識別后的z向位移隨時間變化曲線,如圖11所示,識別激勵曲線與原始激勵曲線對比見圖12.對應的4個極值點和最后1個零點的對比及誤差見表2.

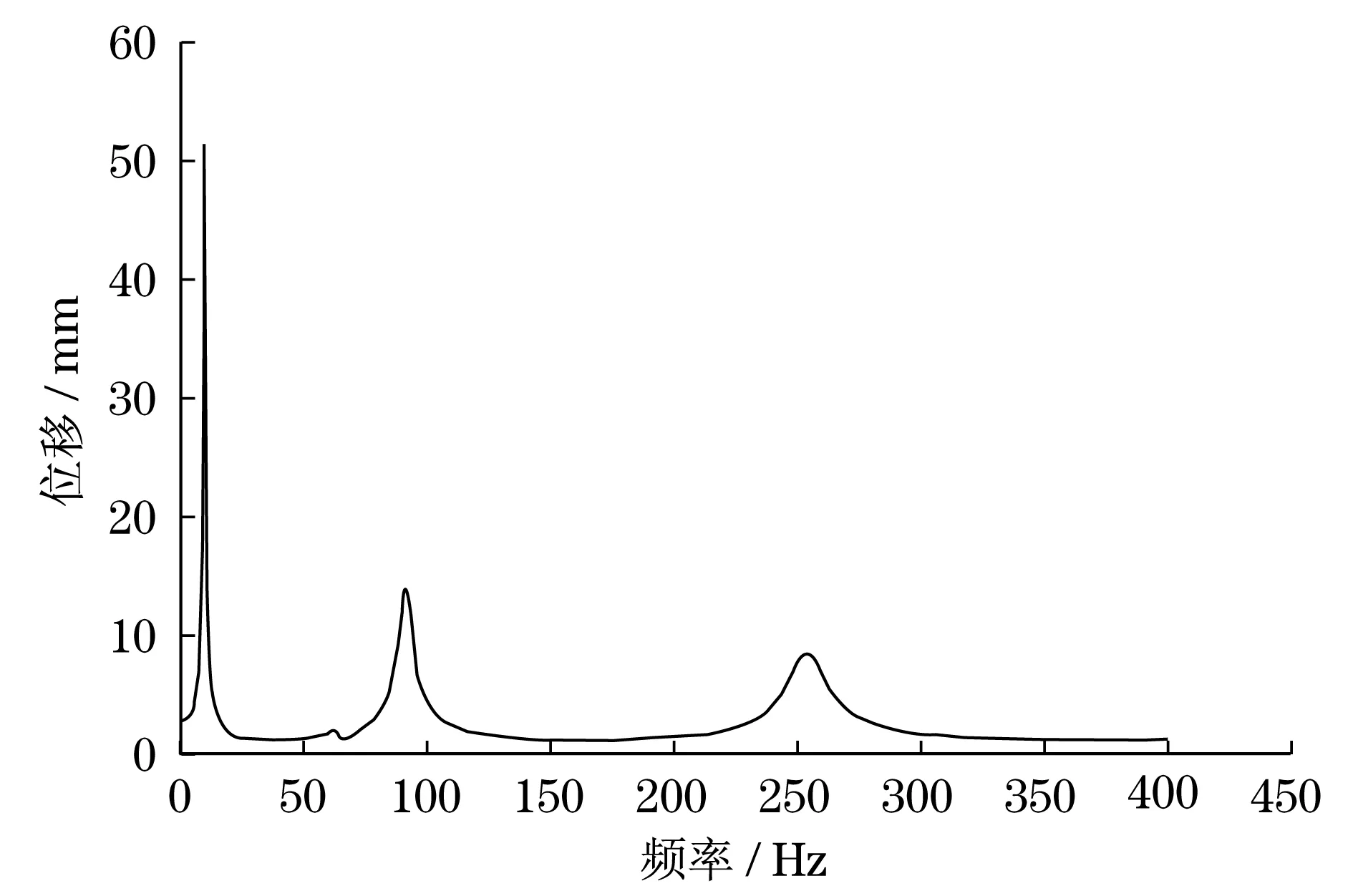
圖8 位移頻率曲線圖Fig.8 Didplacement-frequency curve

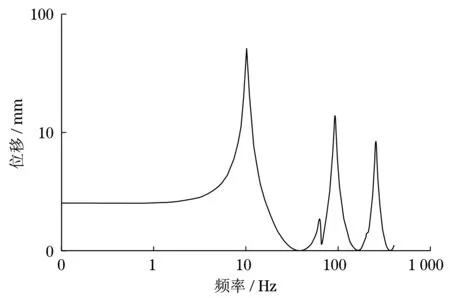
圖9 位移頻率伯德圖Fig.9 Didplacement-frequency Bode

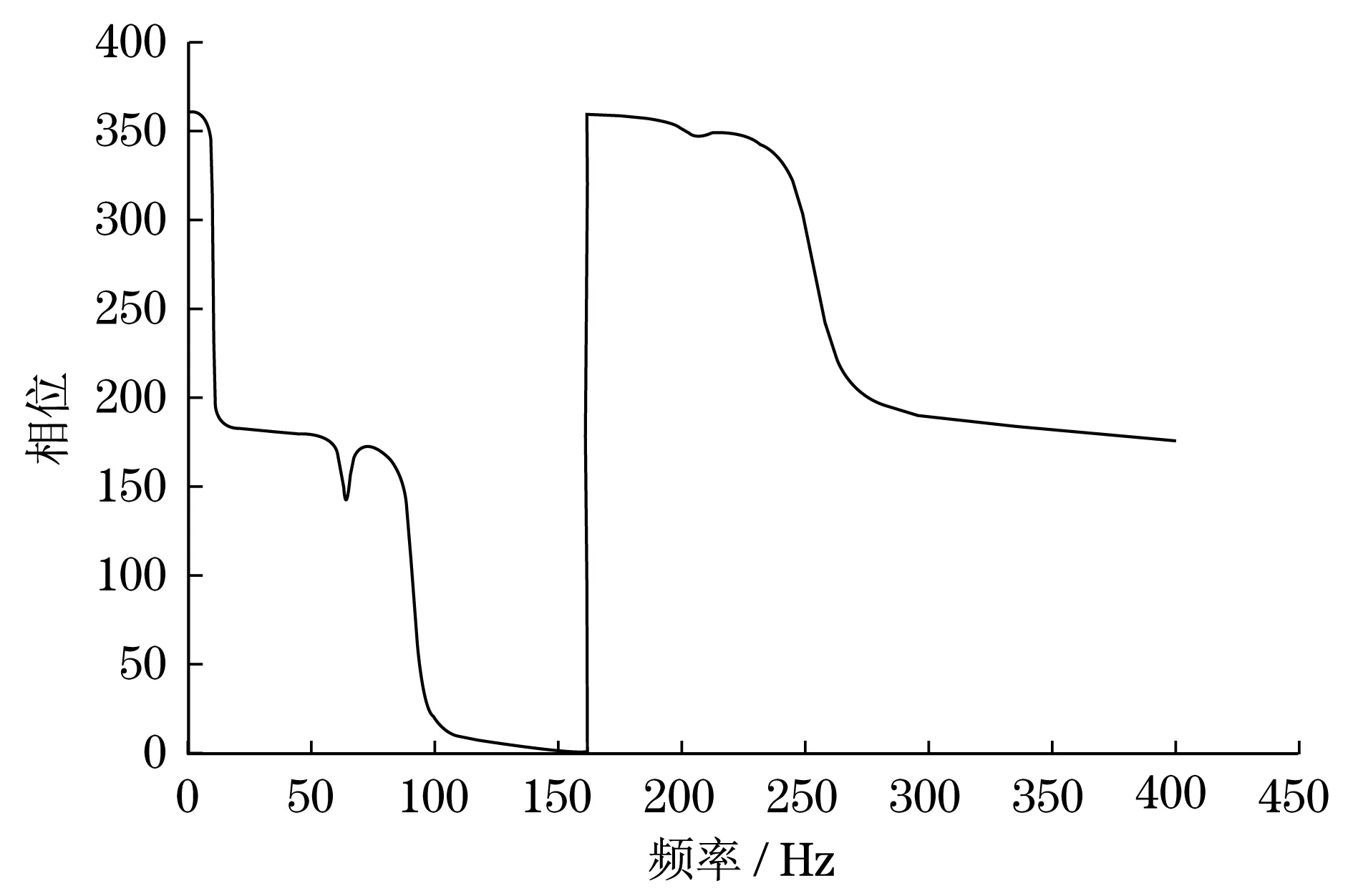
圖10 相位頻率曲線Fig.10 Phase-frequency curve

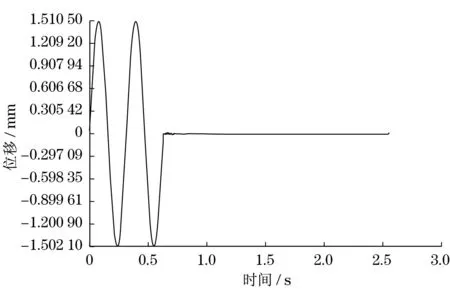
圖11 B點識別的位移激勵時間曲線Fig.11 Didplacement-time curve identified at point B

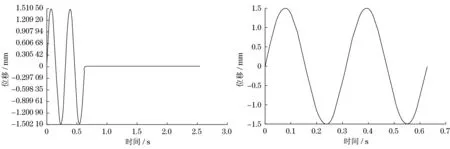
圖12 識別激勵曲線與原始激勵曲線Fig.12 Identified curve and original excitation curve表2 極值點比較Tab.2 Exteme point point value

極值點識別激勵原始激勵誤差%1(0.0775,1.51046)(0.07862,1.5)1.4246-0.69732(0.2325,-1.50213)(0.23585,-1.49998)1.4204-0.14333(0.3925,1.50069)(0.392469,1.49998)-0.0079-0.04734(0.55,-1.49957)(0.549702,-1.5)-0.05420.02875(0.63,0.00767)(0.628319,0.00001)-0.26759.0910

通過圖12和表可知:載荷能很好地識別,并且除了最后一個零點誤差較大外,其他點的誤差不超過2%,可以達到較高的精度.

3 結論

通過上文的理論和模擬,可以得到比較理想的數據結果,驗證了通過頻域法可以進行載荷的識別.這對于解決換熱管的振動識別提供了一種方法,當然在實際中情況比這復雜很多,包括換熱管與折流板之間的間隙以及其他的非線性結構,這些都比本文中的線性結構要復雜.問題雖然復雜,但并不是不可以解決的,相信后續定會有人提出更為全面的解決方法.

[1] 史美中,王中錚.熱交換器原理與設計[M].第四版.南京:東南大學出版社,2009.

SHI Meizhong,WANG Zhongzhrng.Principle and design of heat exchangers [M].4th.ed.Nangjing:Nanjing Southeast University Press,2009.

[2] YETISIR M,FISHER N.Fretting-wear prediction in heat exchanger tubes:the effect of chemical and modeling Ill-defined support conditions[J].ASME Paper PVP,1996,328:359-368.

[3] SAUVE R G.A computational time domain approach to fluidelastic instability for nonlinear tube dynamics[J].ASME Paper PVP,1996,328:327-335.

[4] AXISA F,ANTUNES J,VILLARD B.Random excitation of heat-exchanger tubes by cross-flow[J].J.Fluids Struct.,1990,4:321-341.

[5] BOUCHER K,TAYLOR C.Tube support effectiveness and wear damage assessment in the U-bend region of nuclear steam generators[J].ASME Paper PVP,1996,328:285-296.

[6] ANTUNES J,AXISA F,VENTO M.Experiments on tube/support interaction with feedback-controlled instability[J].ASME J PVT,1992,114:23-32.

[7] FISHER N,TROMP J,SMITH B.Measurement of dynamic interaction between a vibrating fuel element and its support[J].ASME Paper PVP,1996,328:271-280.

[8] MUREITHI N,ITO T,NAKAMURA T.Identification of fuidelastic instability under conditions of turbulence and nonlinear tube supports[J].ASME Paper PVP,1996,328:19-24.

[9] VENTO M,ANTUNES J,AXIAS F.Tube/support interaction under simulates fluidelastic instability:two-dimensional experiments and computations of the nonlinear responses of a straight Tube[J].ASME Paper PVP,1992,242:151-166.

[10] WHISTON G S.Remote impact analysis by use of propagated acceleration signals:theoretical methods[J].Journal of Sound and Vibration,1984,97:35-51.

Vibration loading identification on heat exchange pipes in frequency domain

TIAN Lei, WU Yuan-feng, ZHANG Zheng-xi

(State Nuclear Power Engineering Co., Ltd.Shanghai,201100)

Frequently, the loading identification are resolved in time and frequency domains. As the frequency domain method is applied for heat exchange pipe, a single and linear pipe is successfully used for theoretical deduction and finite element analysis.

heat exchange pipe; loading identification; frequency domain

田 雷(1979-),男,工程師.E-mail:tianlei@snpec.com.cn

O 321

A

1672-5581(2016)05-0464-05