線性二自由度汽車操縱穩定性仿真分析

王　鑫，趙　強，何　法，景　園

(東北林業大學 交通學院，哈爾濱 150040)

?

線性二自由度汽車操縱穩定性仿真分析

王鑫，趙強*，何法，景園

(東北林業大學 交通學院，哈爾濱 150040)

摘要：橫擺角速度和質心側偏角是描述汽車穩定性的兩個重要指標，汽車在高速行駛時，駕駛員緊急轉向會導致車輛失去控制，很容易造成側滑乃至翻車等嚴重交通事故，因此有必要對汽車操縱穩定性進行分析。本文建立了汽車線性二自由度系統的數學模型，應用仿真分析軟件Matlab/sinulink，以前輪轉角為輸入，對系統進行時域分析。比較不同車速、不同前輪轉角和不同輪胎側偏剛度下的穩態響應曲線，分析汽車橫擺角速度和質心側偏角對汽車操縱穩定性的影響。若汽車選用側偏剛度的輪胎，在較低的車速和較小的前輪轉角下行駛，是較為安全的。

關鍵詞：操縱穩定性；穩態響應；橫擺角速度；質心側偏角；側偏剛度

引文格式：王鑫，趙強，何法，等.線性二自由度汽車操縱穩定性仿真分析[J].森林工程，2016，32(1)：64-67.

0引言

車輛穩定性控制是汽車主動安全領域研究的熱點，已有的研究如以車輛橫擺角速度、質心側偏角、輪胎的滑移率、側向加速度及這些變量聯合作為控制變量的控制策略研究[1]，還有通過車輛路面試驗，利用測試方法獲得試驗車輛操穩性能的物理參數，用來對操縱穩定性進行定量的評價[2-4]。國外一些學者對質心側偏角影響汽車穩定性的表征進行了深入研究，運用 “β-method”分析了質心側偏角對橫擺力矩和側向力的影響，從而闡述了質心側偏角與穩定性的關系[5]。考慮到橫擺角速度和質心側偏角是描述汽車穩定性的兩個重要指標，本文建立汽車兩自由度轉向模型，采用Matlab/sinulink軟件仿真不同車速、前輪轉角和不同輪胎側偏剛度下橫擺角速度和質心側偏角響應特性，并以此分析汽車的操縱穩定性。

1線性二自由度汽車模型

為了便于分析操縱穩定性的基本特性，做如下簡化和假設：忽略轉向系統的影響，將輸入直接施加于車輪；忽略地面切向力對輪胎側偏特性的影響；忽略空氣動力和汽車懸架的作用[6-7]，得到線性二自由度的汽車操縱穩定性模型如圖1所示。

根據上述對模型的假設并參照圖1，列出二自由度汽車坐標系的側向和橫擺動力學平衡方程為：

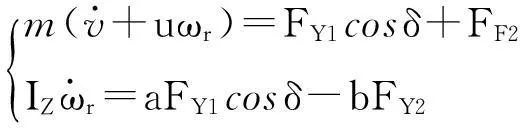
(1)

式中：m是汽車質量；Iz是汽車的轉動慣量；v為縱向速度；ωr為橫擺角速度；a、b分別為汽車前、后軸至質心的距離；δ為前輪轉角；FY1、FY2分別為地面對前、后輪的側向反作用力，也稱側偏力。

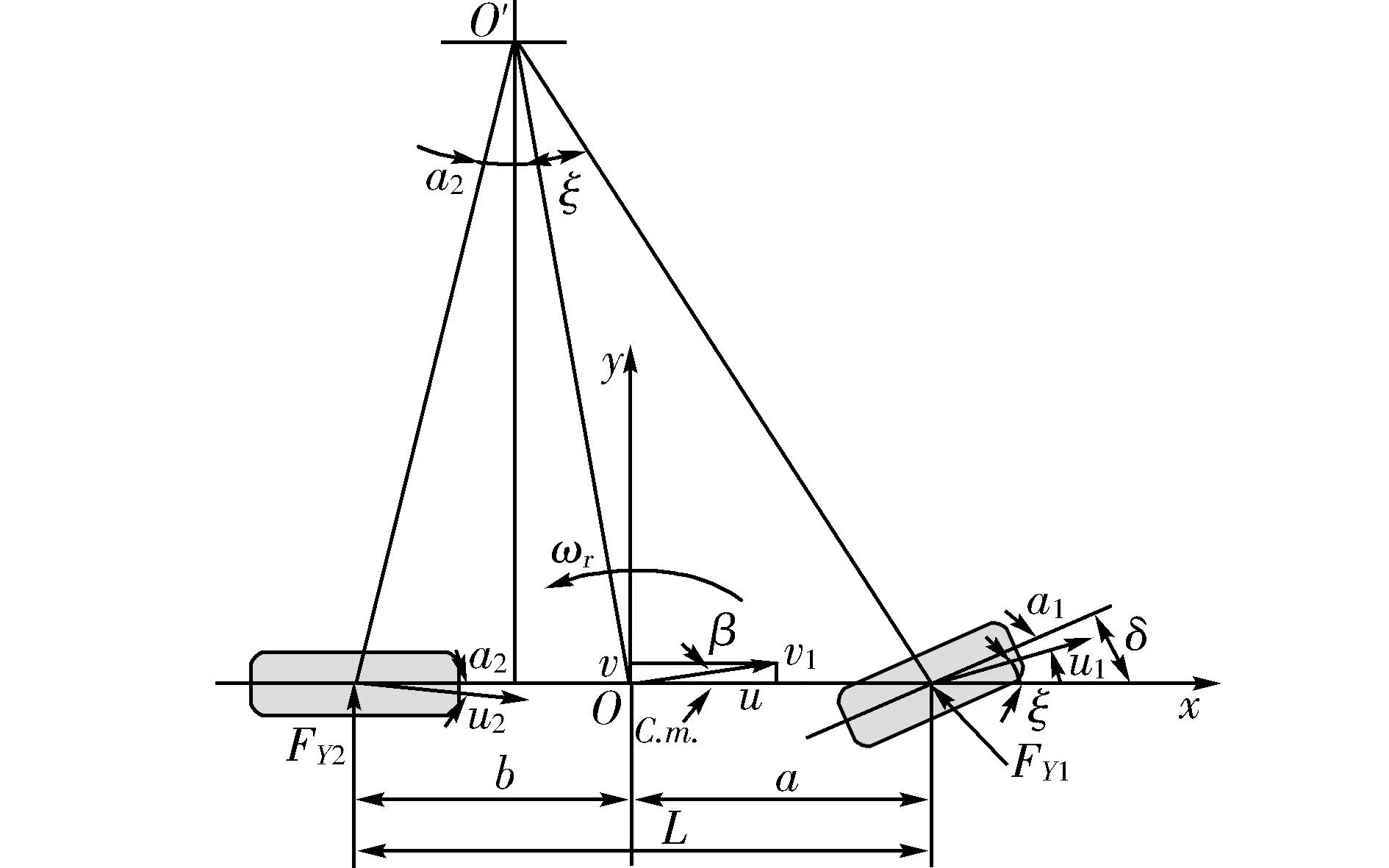
圖1　線性二自由度模型Fig.1 Linear two degrees of freedom model

考慮到前輪轉角δ較小，前輪和后輪所受到的側向力與相應的側偏角成線性關系，FY1、FY2可寫作：

(2)

式中：α1、α2為前、后車輪的側偏角；k1、k2為前、后車輪的側偏剛度；β為質心側偏角。

將公式(2)代入公式(1)，消去α1和α2，整理后得二自由度汽車運動微分方程為：

(3)

2前輪轉角階躍輸入下的時域響應

在上述模型下，簡要討論車輛模型對方向盤角階躍輸入下的時域響應。車輛以勻速直線運動的狀態前進時，行駛到某一設定時刻強制給予方向盤一定的轉角并保持此角度恒定，也就稱作為方向盤角階躍輸入[8]。通常情況下，車輛在輸入給定的一段時間以后，會進入到勻速圓周運動狀態，此狀態也就是車輛對角階躍輸入下的穩態響應。從方向盤角階躍輸入開始到車輛剛進入穩定狀態的這個過程，即車輛從勻速直線運動狀態到勻速圓周運動的時間里的響應，稱為角階躍下的瞬態響應[9]。

車輛在轉向時要保證所有輪胎純滾動狀態，來減少輪胎磨損和提高車輛行駛穩定性，車輛要圍繞轉向中心作曲線運動來驗證車輛穩定性的好壞。車輛在前輪角階躍輸入下的穩態響應，稱為車輛的穩態轉向特性，它是衡量車輛穩定性的主要指標之一。當車輛以固定的車速轉彎行駛時，若轉角保持不變，車輛行駛的圓周運動也不變，此時緩慢增加車速，車輛向外偏離圓周運動軌跡的特性稱作過度轉向特性，車輛向內偏離圓周運動軌跡的特性稱作不足轉向特性，轉向加速時車輛仍保持原有的運動軌跡，稱為中性轉向特性[10]。

3Matlab/Simulink仿真研究

本文使用Matlab/Simulink進行轉向穩定性的仿真分析。以某轎車的參數(見表1)為例建立汽車二自由度轉向模型，如圖2所示。通過仿真試驗分析不同前輪轉角和不同車速下橫擺角速度和質心側偏角對汽車操縱穩定性的影響。

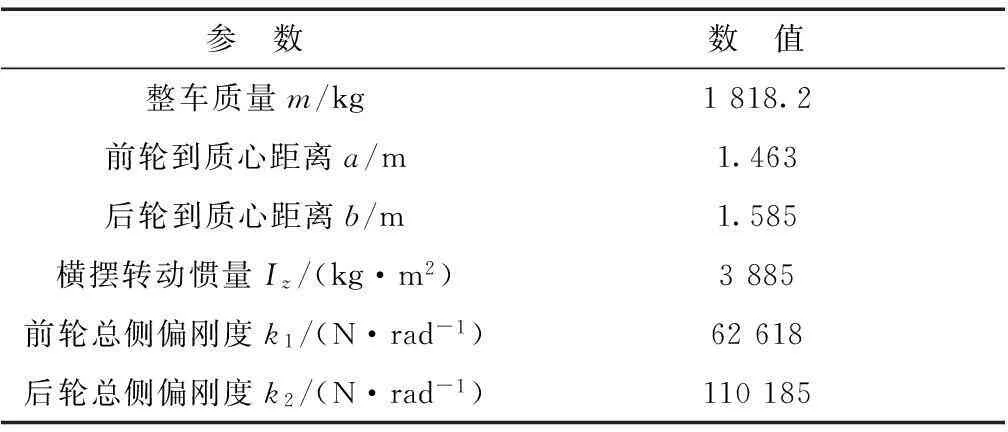
表1　車輛相關參數

3.1特征車速

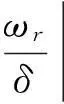
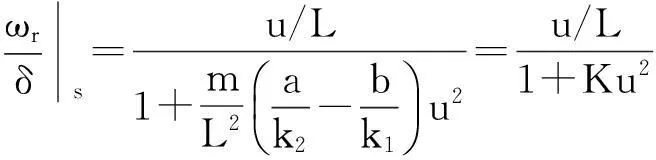
(4)

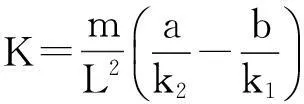
(5)

式中：K稱為穩定性因數，s2/m2，它是表征汽車穩態響應的一個重要參數。

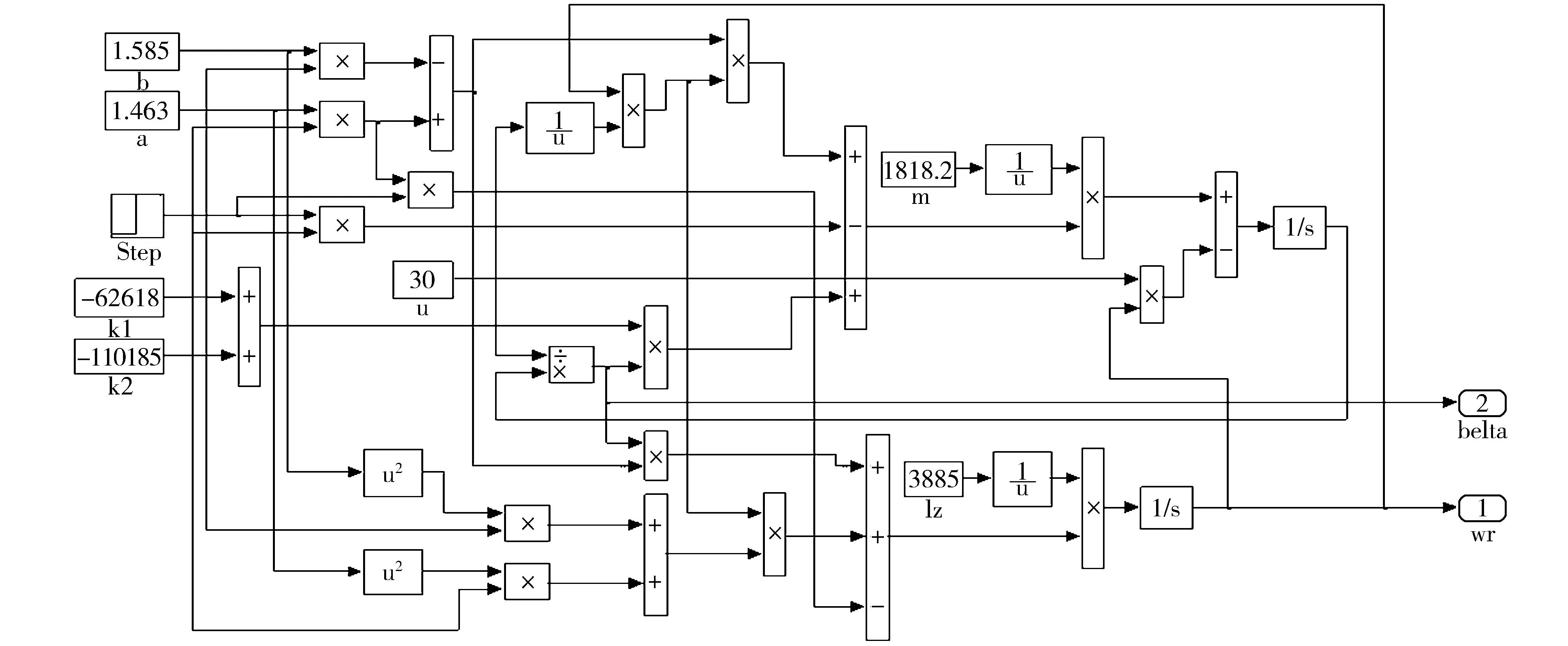
圖2　汽車二自由度轉向模型Fig.2 Two degrees of freedom vehicle steering model

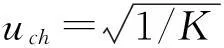
3.2不同前輪轉角下的對比

汽車以30m/s的速度行駛，在仿真時間為1s時給前輪一個階躍信號，分別使前輪轉角由0°分別轉到5°、10°、15°，并保持此角度不變。此時橫擺角速度響應曲線如圖3所示，質心側偏角響應曲線如圖4所示。

由圖3可以看出，隨著前輪轉角的增加，橫擺角速度的超調量逐漸增大，進入穩態所經歷的時間略微增加，前輪轉角為15°時橫擺角速度最先到達穩態值，上升時間最短，車輛的穩定性和可控制性變差[12]。

由圖4可以看出，隨著前輪轉角的增大，汽車質心側偏角明顯增大，固有圓頻率及阻尼比減小，超調量及穩定時間增加，因此應該避免在高速行駛時急轉方向盤產生大的前輪轉角。

3.3不同車速下的對比

汽車分別以10、15、20、25、30m/s的速度行駛，在仿真時間為1s時給前輪一個階躍信號，使前輪轉角由0°轉到10°，并保持此角度不變。此時橫擺角速度響應曲線如圖5所示，質心側偏角響應曲線如圖6所示。

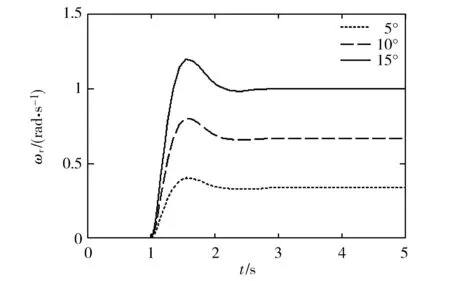
圖3　不同前輪轉角下的橫擺角速度響應曲線Fig.3 The yaw rate response curve under different front wheel angle

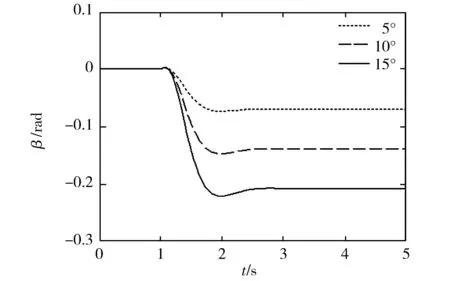
圖4　不同前輪轉角下的質心側偏角響應曲線Fig.4 The sideslip angle response curve underdifferent front wheel angle

根據上一節知識能夠計算出該車不足轉向的特征車速為20 m/s，此車速是衡量不足轉向特性的重要指標。由圖5可以看出，隨著車速的增加，車輛橫擺角速度的超調量逐漸變大，達到穩態值所用的時間增加，車輛不穩定性變差，難以操控；當車速小于20 m/s時，橫擺角速度的穩態值隨著車速的增加而增加，而當車速小于20 m/s時，橫擺角速度的穩態值隨著車速的增加而減少。

由圖6分析得出，汽車的質心側偏角隨著車輛速度的增大由正值變為負值，且逐漸增大。其進入穩態所經歷的時間也增加。當該車輛車速超過特征車速20 m/s時，質心側偏角迅速增大，超過該車輛穩定的臨界值，車輛的操縱穩定性下降，極有可能產生打滑急轉和側翻現象，以至于發生交通事故，危害人身安全。

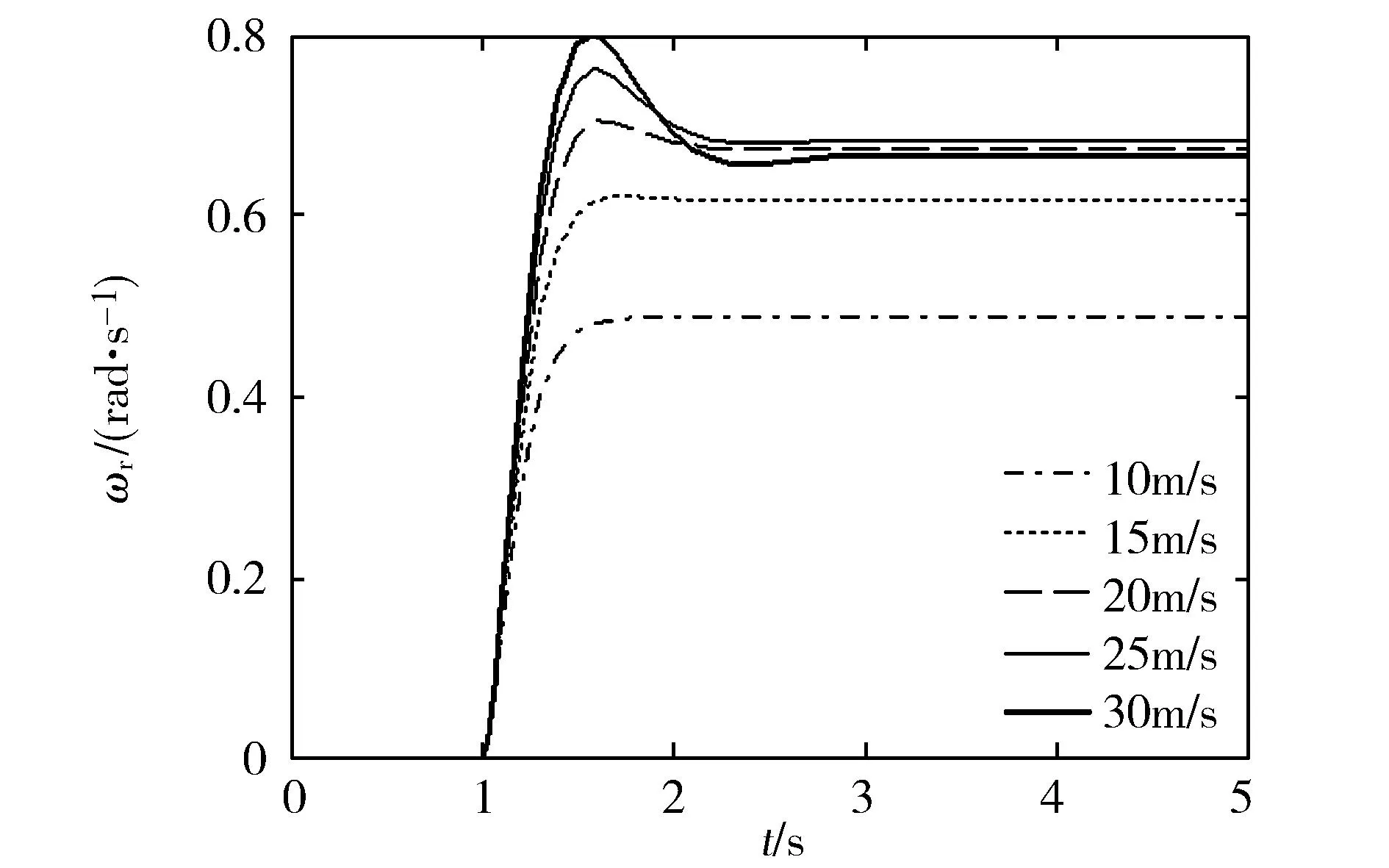
圖5　不同車速下的橫擺角速度響應曲線Fig.5 The yaw rate response curve under different speeds

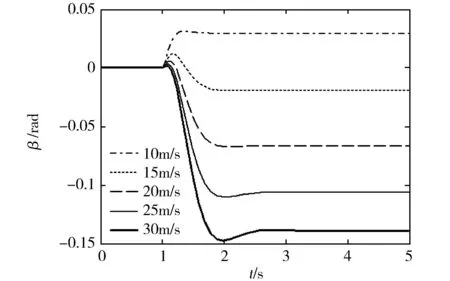
圖6　不同車速下的質心側偏角響應曲線Fig.6 The sideslip angle response curve under different speeds

3.4不同輪胎側偏剛度下的對比

輪胎的側偏特性如圖7所示，由側偏力和側偏角的關系曲線可知，側偏角小于5°時，側偏力與側偏角成線性關系，側偏角超過5°時，側偏角以較大的速率增長，使曲線斜率逐漸減小，此時輪胎部分接地面已經發生側滑，直至側偏力達到附著極限時，輪胎產生完全側滑。顯然，輪胎的最大側偏力由垂直載荷決定。總而言之，側偏剛度是決定汽車操縱穩定性的重要輪胎參數[13]，較高的側偏剛度可以保證汽車良好的操縱穩定性。

選用兩組側偏剛度不同的輪胎，側偏剛度分別為k1=62 618 N/rad，k2=110 185 N/rad；k1=44 880 N/rad，k2=51 154 N/rad。汽車均以10 m/s的速度行駛，在仿真時間為1s時給前輪一個階躍信號，使前輪轉角由0°轉到10°，并保持此角度不變。此時橫擺角速度響應曲線如圖8所示。

對比圖8中曲線可得，汽車在行駛速度相同，前輪轉角輸入一樣的情況下，較大的輪胎側偏剛度，使汽車對前輪角階躍輸入的響應時間短，反應快，可較好的控制車身的姿態[14]，該結論與上述輪胎側偏特性相符合。

圖7　輪胎側偏特性Fig.7 Tire lateral characteristics

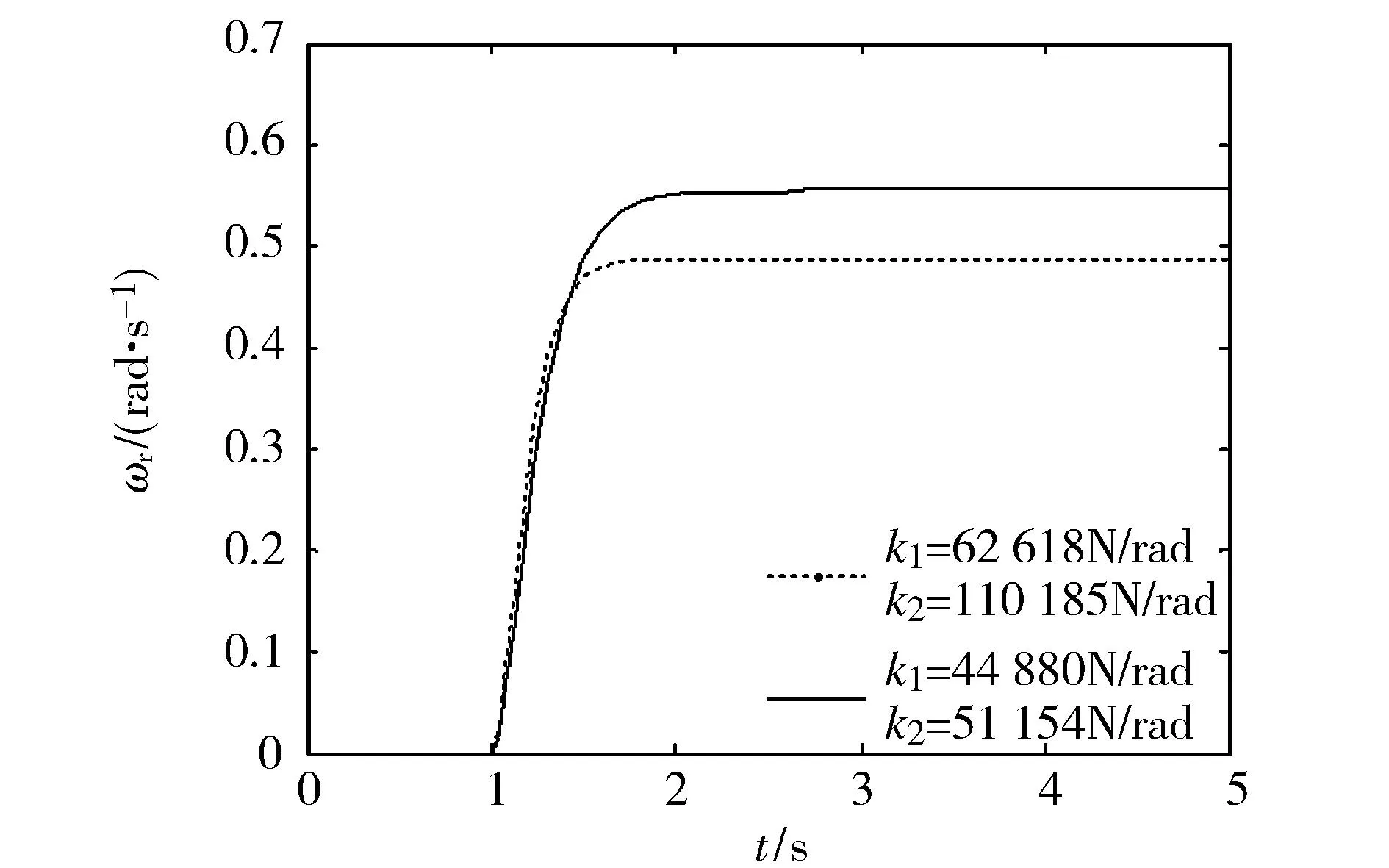
圖8　不同輪胎側偏剛度下的橫擺角速度響應曲線Fig.8 The yaw rate response curve underdifferent tire lateral stiffness

4結論

針對整車線性二自由度汽車簡化模型，運用Mattlab/simulink仿真軟件，以階躍信號為前輪轉角輸入，得出橫擺角速度和質心側偏角對前輪轉角的響應特性曲線。通過對各個曲線的分析，根據轉向特性在不同情況下的響應，闡述了橫擺角速度、質心側偏角和輪胎側偏剛度對車輛操縱穩定性的影響，及其與車速和前輪轉角的內在關系，為以后車輛穩定性的研究和探索提供了基本的參考和借鑒價值。

【參考文獻】

[1]周紅妮，陶健民.質心側偏角和橫擺角速度對車輛穩定性的影響研究[J].湖北汽車工業學院學報，2008，22(2)：6-10.

[2]喬邦，張才權，李靜紅.汽車操縱穩定性道路試驗研究[J].新余學院學報，2013，18(6)：79-81.

[3]周文，喻澤文.道賀高速公路安全審計及改善措施[J].公路工程，2011，36(1)：119-122.

[4]童申家，王培.風壓對車輛橫向穩定性的影響[J].公路工程，2012，37(5)：104-107.

[5]Shibahata Y，Shimada K，Tomari T.Improvement of vehicle maneuverability by direct yaw moment control[J].Vehicle System Dynamis，1993，22(5/6)：465-481.

[6]王霞，張麗.汽車操縱穩定性動力學仿真[J].沈陽航空工業學院學報，2009，26(4)：24-26.

[7]朱春俠，張韶回，李勁松.輪胎對汽車操縱穩定性的影響分析[J].農業裝備技術，2011，37(3)：28-30.

[8]宮喚春，徐勝云，杜瑩，等.汽車操縱穩定性試驗仿真分析研究[J].公路與汽運，2014(5)：6-9.

[9]蘇小平，羅亮.某轎車轉向瞬態響應特性仿真分析[J].科學技術工程，2014，14(3)：259-262.

[10]余志生.汽車理論(5版) [M].北京：機械工業出版社，2009.

[11]陳蓉.轉向盤轉角階躍輸入下汽車操縱穩定性仿真分析[D].長春：吉林大學，2006.

[12]唐智宏，李強，程峰，等.基于駕駛員-EPS閉環系統汽車操縱穩定性的研究[J].森林工程，2008，24(5)：32-34.

[13]李亮平，蘇初旺，謝美芝，等.汽車電子穩定程序控制策略的研究[J].森林工程，2009，25(5)：47-50.

[14]岳喜磊，王紅巖，賀小軍.輪胎側偏特性對汽車前輪角階躍輸入瞬態響應影響的研究[J].裝甲兵工程學院學報，2006，20(4)：40-44.

Simulation Analysis on Automobile HandlingStability with Linear Two Degrees of Freedom

Wang Xin，Zhao Qiang*，He Fa，Jing Yuan

(Traffic College，Northeast Forestry University，Harbin 150040)

Abstract：Vehicle yaw rate and sideslip angle are the important indexes of describing vehicle stability.When the car is driving at high speed，the driver’s emergency steering will lead to losing control of the vehicle.It is easy to cause serious traffic accidents of the sliding and overturning.Therefore，it is necessary to analyze the automobile handling stability.The paper established the car linear mathematical model of two degrees of freedom system by applying the simulation analysis software Matlab/simulink.The front wheel angle was treated as the input，and the time domain method was used to analyze the system.The steady state response curves under different speed，different angle，and different tire lateral stiffness were compared and the influences of automobile yawing angular velocity and sideslip angle on the vehicle handling stability were analyzed.If choose cornering stiffness bigger tires,driving is relatively safe at lower speed and smaller Angle.

Keywords：handling stability；steady state response；yaw rate；sideslip angle；lateral stiffness

*通信作者：趙強，博士，教授。研究方向：載運工具裝備設計與功能創新。E-mail：qyangzhao@163.com

作者簡介：第一王鑫，碩士研究生。研究方向：載運工具運用工程。

基金項目：黑龍江省留學歸國人員科學基金(LC2015019)

收稿日期：2015-07-19

中圖分類號：S776；U 461.6

文獻標識碼：A

文章編號：1001-005X(2016)01-0064-04