一種基于倒排索引的多維網絡存儲模型

張志遠，徐恒盼

(中國民航大學 計算機科學與技術學院，天津 300300)

一種基于倒排索引的多維網絡存儲模型

張志遠，徐恒盼

(中國民航大學 計算機科學與技術學院，天津 300300)

具有多維屬性的實體相互連接構成的網絡(如社交網絡)稱為多維網絡，在多維網絡上支持聯機分析處理具有重要的應用價值。現有方法大都從文件或數據庫中逐條讀取記錄，當數據量很大時，需要多次讀取磁盤，導致查詢響應時間過長，效率較低。文中提出了一種新的基于倒排索引的多維網絡存儲模型II-GC(Inverted Index based Graph Cube)，通過將圖的拓撲結構和頂點的多維屬性存儲在倒排索引列表中加快查詢速度，并給出了在多維網絡上進行聚集查詢(cuboid)和交叉查詢(crossboid)的算法。在DBLP數據集上的實驗表明，該模型較GraphCube的查詢效率更高，擴展性更好。

多維網絡；圖立方體；倒排索引；聯機分析處理

0 引 言

隨著Web2.0等互聯網新概念的飛速發展，大量新型社交網絡服務不斷涌現，社交網絡在人們的生活中扮演著越來越重要的角色。作為一個交叉領域，社交網絡研究已經得到國內外學者們的廣泛關注。目前對于社交網絡的研究多集中于其拓撲結構，如社區劃分[1-2]、輿情傳播[3]等。在實際應用中，除拓撲結構外，與頂點相關的多維屬性信息也非常重要，如統計合著網絡中的男女比例及連接關系等。文中主要研究由拓撲結構及與頂點關聯的多維屬性一起構成的多維網絡[4]。

對多維網絡進行OLAP[5]分析可展現不同尺度上的網絡結構特征，如聚集操作可分析合著網絡中不同領域人員之間的網絡結構，切片操作可分析某特定領域如數據挖掘學者之間的網絡關系。為突破傳統OLAP技術無法支持帶有圖結構的復雜網絡分析的限制，近年來研究人員開展了很多相關研究。2007年吳巍[6]提出了Link OLAP的概念，將面向實體的分析擴展為面向連接的分析，以復雜網絡可視化為基礎，突破了以往傳統OLAP系統中單調的二維表格表現方式。同年，Chen等[7]提出了Graph OLAP的概念，將OLAP技術引入到復雜網絡分析中，實現了在信息維和拓撲維兩種維度上的OLAP操作。2010年，Li等[8]提出了一種適合Graph OLAP的數據倉庫概念模型，即雙星模型，并提出了信息維聚集算法I-OLAPing和拓撲維聚集算法T-OLAPing。2011年，Li等[9]又在原有基礎上提出了基于信息網絡數據倉庫和信息網絡數據立方體的概念，提出了雙星座數據模型，實現了信息維和拓撲維的聚集算法以及上卷下鉆的OLAP操作。同年，Zhao等[10]詳細介紹了一個新的數據倉庫模型，即基于圖的數據立方體Graph Cube，同時提出了用于Graph OLAP的新的查詢方式crossboid(詳見定義4)，并討論了Graph Cube的物化策略。2011年，Qu等[11]提出了一種信息網絡拓撲維的框架，并基于此框架提出了更高效的查詢方法以及數據立方體的物化策略，對拓撲維在線分析處理(T-OLAP)操作中特定類型度量的優化進行了有針對性的深入分析。

現有的GraphCube OLAP聚集算法研究大多是直接對文件或數據庫中的數據進行聚集查詢，逐條檢索記錄，判斷是否符合條件。當文件很大時，往往要多次讀寫磁盤，較為耗時。文中提出了一種新的多維網絡存儲模型II-GC(Inverted Index based Graph Cube)，通過引入倒排索引技術，把直接對數據庫中數據進行的聚集查詢轉化成倒排索引集合間的交、并運算，不用逐個讀取記錄，參與運算的數據大幅減少，提高了檢索速度。

1 基本概念

定義1：多維網絡[4,12]。多維網絡是一個形式為G=(V,E,A)的圖，其中V是頂點集合，E?V×V是邊的集合，A={A1,A2,…,An}是與頂點相關聯的屬性集合。任取v∈V，存在一個多維元組A(v)=(A1(v),A2(v),…,Am(v))，其中Ai(v)是頂點v上的第i個屬性，1≤i≤m。

圖1是一個社交網絡中的多維網絡示例。圖中有10個頂點，記作v1,v2,…,v10，分別代表社交網絡中不同的個體；13條邊分別代表個體間的關系。每個頂點均關聯一個多維屬性元組，記錄該個體的基本信息，包括ID，Gender，Location及Profession。所有頂點的多維屬性元組集合構成多維屬性表，如表1所示。

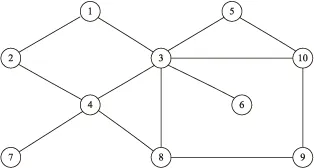
圖1 一個社交網絡的多維網絡圖

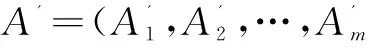
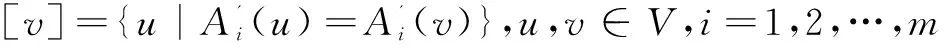
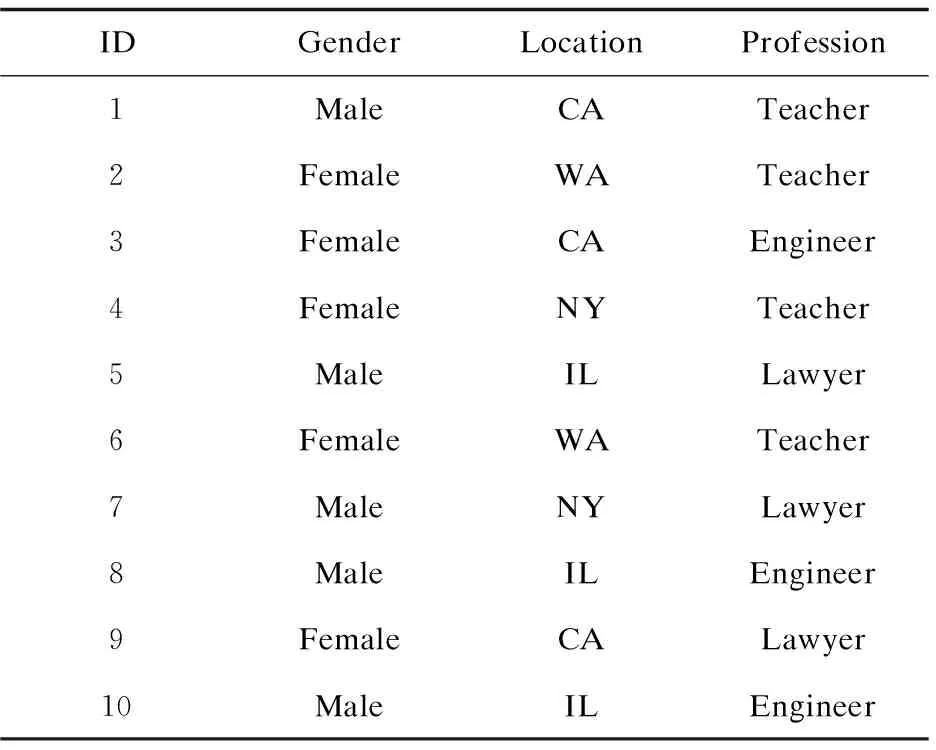
表1 多維屬性表

(2)?u',v'∈V'，其中u'代表[u]，v'代表[v]，令E(u',v')={(u,v)|u∈[u],v∈[v],(u,v)∈E}，若E(u',v')非空，則?e'∈E代表E(u',v')。邊的權重ω(e')=Fe(E[u',v'])，其中Fe()為作用在邊上的聚集函數，稱e'為聚集邊。

以圖1中的“社交網絡”為例，選取A的一種聚集A'=(Gender，*，*)，以Count()作為頂點和邊上的聚集函數，則產生的聚集網絡含Male和Female兩個聚集頂點，其權重值分別為男女實例的個數，本例中均為5。邊的權重代表聚集頂點間的關系，如Female頂點集合{v2,v3,v4,v6,v9}中有三條邊連接，即v2v4,v3v4,v3v6，因此其權重為3。

定義3：圖立方體[10]。給定多維網絡(V,E,A)，根據A的所有可能的聚集產生的聚集網絡集合構成圖立方體(GraphCube，GC)，其每個聚集網絡又被稱為cuboid。

仍以圖1中的社交網絡為例，頂點代表在不同的聚集屬性下得到的聚集網絡，邊代表不同的聚集網絡間的父子關系，其中(Gender，Location，Profession)是所有其他聚集網絡的基礎，(*，Location，Profession),(Gender，*，Profession)及(Gender，Location，*)均可從(Gender，Location，Profession)直接求得。

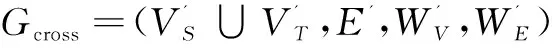
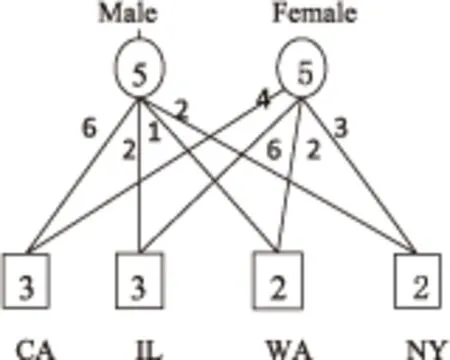
圖2 crossboid查詢產生的聚集網絡

2 II-GC存儲模型

多維網絡可看作是具有多維屬性頂點的網絡圖，節點的屬性信息可存儲在其data域中，也可像表1一樣將所有頂點信息存儲在一個二維表格中。在進行聚集操作時，兩種方式均需要對圖進行遍歷，時間復雜度為O(n+e)。其中，n是頂點個數，e是邊的條數。隨著網絡規模的增加，這種線性復雜度甚至都是不能忍受的。為此文中提出基于倒排索引的多維網絡存儲模型，將所有信息存儲在頂點的倒排索引和邊的倒排索引中，如圖3所示。

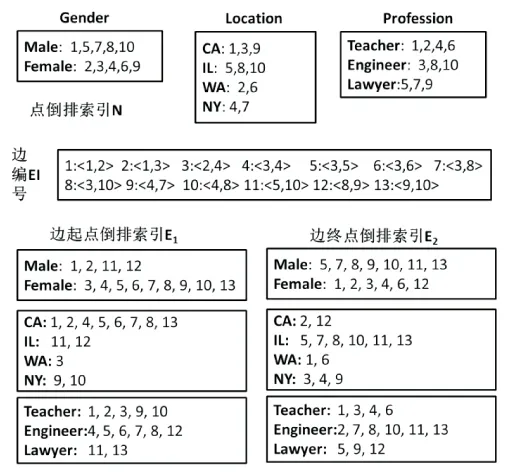
圖3 基于倒排索引的多維網絡存儲模型

按照廣度優先的遍歷順序對點和邊進行編號，2.1節中討論了這種編號方式帶來的好處。邊的倒排索引按起點和終點分為兩組，對如圖1所示的無向圖，以數字較小的頂點為起點。例如邊起點倒排索引中的Male：1,2,11,12表明有四條邊的起點中Gender屬性為Male。起點倒排索引中的Male和終點倒排索引中的Male交集只含有11這一條邊，因此可以確定Male和Male之間的連接邊只有一條，正好回答了Male自身連接權重的問題。采用基于倒排索引的存儲模型至少有以下幾個優點：

(1)將圖遍歷轉換為集合的交并操作，加快了查詢速度；

(2)采用倒排索引壓縮算法可進一步減少存儲空間；

(3)相對于結構復雜的圖來說，基于倒排索引的查詢更容易并行化。

2.1 模型初始化

將多維網絡轉換為基于倒排索引的存儲模型，初始化算法如下：

輸入：一個多維網絡G=(V,E,A)；

輸出：點倒排索引表N，邊倒排索引表E1,E2，邊編號索引表EI。

begin

//按廣度優先順序對圖節點編號

初始化隊列Q，并將v1加入Q;

nodeno←0;設置所有節點為未訪問;

whileQ非空{

從隊列中取出一個頂點u并標記為已訪問;

u.id=++nodeno;

foru的每個未訪問過的鄰居節點v{

ifv不在Q中則將其加入隊列Q;

}

}

//對圖廣度優先遍歷并設置倒排索引表

初始化隊列Q，并將v1加入Q;

edgeno←0;設置所有節點為未訪問;

whileQ非空{

從隊列中取出一個頂點u并標記u為已訪問;

for除id外的每一個屬性Ai{

N(Ai(u))←N(Ai(u))∪{u.id}；

}

foru的每個未訪問過的鄰居節點v{

EI[++edgeno]←(u.id,v.id);

for除id外每一個屬性Ai{

E1(Ai(u))←E1(Ai(u))∪{edgeno};

E2(Ai(u))←E2(Ai(v))∪{edgeno};

}

ifv不在Q中則將其加入隊列Q;

}

}

end

按廣度優先順序對圖節點和邊進行編號，這樣可保證點和邊的倒排索引列表按升序排列，為后面的求交操作帶來便利。算法相當于對原圖進行了兩次廣度優先遍歷，其時間復雜度亦為O(2n+2e)。采用倒排索引格式存儲后，原多維網絡不必繼續保留。若采用的聚集函數為Count()，則邊編號索引表EI也可以去掉。由于倒排索引存儲的均為整數，和原來使用大量字符串相比存儲空間有所減少。需要注意的是，該存儲模型對類別較多的列屬性(如姓名)而言是低效的，因為這會造成大量的短倒排索引列表，不利于后面的查詢操作。

2.2 cuboid查詢

以聚集A'=(Gender,*,*)為例，Gender對應的屬性值有Male和Female，查看相應的點倒排索引表N得：N(Female)={2,3,4,6,9}，N(Male)={1,5,7,8,10}。說明Female和Male分別有5人。然后再查他們之間的連接關系得：E1(Male)={1,2,11,12}，E2(Male)={5,7,8,9,10,11,13}。兩者的交集為{11}，說明以Male為起點和終點的邊只有1條。同理可得E1(Female)∩E2(Female)={3,4,6}，說明以Female為起點和終點的邊共有3條。連接Male和Female之間的邊或者以Male為起點，或者以Female為起點，對應的集合為{E1(Male)∩E2(Female)}∪ {E1(Female)∩E2(Male)}={1,2,5,7,8,9,10,12,13}，說明Male和Female之間有9條邊。Cuboid查詢算法如下：

輸入：倒排索引多維網絡IIG=(N，E1，E2，EI)，聚集屬性A'；

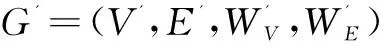
begin

V'←?;E'←?;

//計算所有可能的聚集頂點

Vt1←?;Vt2←?;

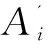
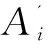
ifV'為空集{V'←Vt1;continue;}

forV'的每一個元素v'{

forVt1的每一個元素vt1{

Vt2←Vt2∪{v',vt1};

}}

V'←Vt2;Vt1←?;Vt2←?;

}

//計算頂點的權重

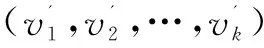
if(T==?){將v'從V'中刪除;continue;}

}

//計算邊的權重

forV'的每一個頂點對(u',v'){

if(u'≠v'){

e←e∪e';

}

if(e≠?) {

{E'←E'∪{(u',v')};

}

}

end

設cuboid聚集網絡有m個頂點，每個頂點有k個分量(如Male,Professor)，則算法最多需要2m2k+mk次求交集操作，而實際上會小得多，因為求交集時集合大小隨著次數的增加將明顯變小，當結果為空時即可停止。

2.3 crossboid查詢

以(Gender，*，*)和(*，Location，*)為例，對兩個聚集屬性依次應用2.2中算法的前兩步得6個聚集節點：Male(5)，Female(5)，CA(3)，WA(3)，NY(2)，IL(2)。其中括號內的值為點的權重。然后應用邊倒排索引查詢連接邊，例如Male和CA之間的連接為：(E1(Male)∩E2(CA))∪(E1(CA)∩E2(Male))=([1,2,11,12]∩[2,12])∪([1,2,4,5,6,7,8,13]∩[5,7,8,9,10,11,13])=[2,5,7,8,12,13]。因此Male和CA之間的連接權重為6。crossboid查詢算法如下：

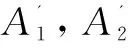
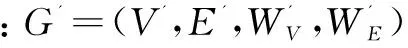
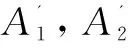
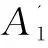
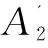
//求S和T的連接邊及權重

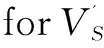
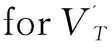
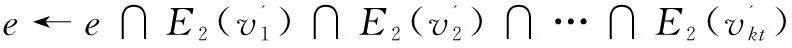
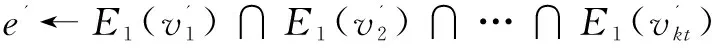
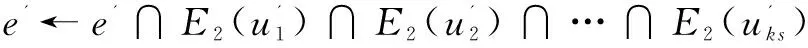
e←e∪e'；

if(e≠?) {

E'←E'∪{(u',v')};

}

}

}

2.4 雙二分查找

倒排索引源于實際應用中需要根據屬性的值來查找記錄。這種索引表中的每一項都包括一個屬性值和具有該屬性值的各記錄的地址。由于不是由記錄來確定屬性值，而是由屬性值來確定記錄的位置，因而稱為倒排索引。利用倒排索引查詢的時間復雜度主要取決于集合求交的過程，注意到所有的倒排索引列表都是升序排列的，可以采用雙二分查找算法[13]提高查找速度。對于兩個有序集合D和Q，假設D比Q的元素多。該算法首先在D中對Q的中間值Qmid進行二分查找，若找到則將Qmid添加至結果集R中。無論是否找到，都可以將D和Q劃分為兩個部分：D1，D2以及Q1，Q2。其中D1和Q1中的所有元素都小于Qmid，D2和Q2中的所有元素都大于Qmid。如此，問題轉換為求D1和Q1的交集及D2和Q2的交集。實際過程中可先比較兩個集合的最大最小值判斷其交叉重疊部分，從而減少比較集合的大小。Ricardo指出，當兩個集合的元素個數相差較大時，該算法的復雜度為O(mlg(n))。其中m和n分別為短集合和長集合的元素個數[14]。由于需要進行多次求交運算，結果集合肯定會越來越短，因此適合采用雙二分查找。

3 實驗結果與分析

3.1 實驗數據集

從1969年到2014年的DBLP數據集中選取四個領域的會議文章共289 135篇，按作者統計文章發表情況建立了合著關系網絡，含34 259個作者作為頂點，193 902個作者之間的合作關系為邊。頂點屬性信息為Author、Area、Year、Productive。共包含4個Area，每個Area選取5個代表性會議：數據庫(SIGMOD，VLDB，ICDE，PODS，EDBT)、數據挖掘(KDD，ICDM，SDM，PKDD，PAKDD)、信息檢索(SIGIR，WWW，CIKM，ECIR，WSDM)和人工智能(IJCAI，AAAI，ICML，CVPR，ECML)。若作者在多個領域發表文章，選擇文章數量最多的領域為其Area。Productive根據作者發表的文章篇數分為四個類別：excellent(35篇以上)、good(15到34篇)、fair(3到14篇)以及poor(小于3篇)。

3.2 cuboid查詢實驗

本小節對比II-GC和GraphCube[10]的cuboid查詢在不同規模多維網絡上的響應時間。網絡邊數從1萬到6萬變化時的cuboid查詢響應時間對比如圖4所示。

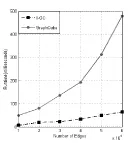
圖4 不同規模網絡上的cuboid查詢對比

可以看出，II-GC比GraphCube上的cuboid查詢響應時間短，且隨著復雜網絡邊數的增加，II-GC的查詢響應時間變化不大，而GraphCube的查詢時間則迅速增加。

聚集維度從1到3變化時，兩者的cuboid查詢響應時間對比如圖5所示。

圖5 不同維數上的cuboid查詢對比

可以看出，II-GC的cuboid查詢響應時間更短，且隨著維數的增加，II-GC的查詢響應時間呈線性增長，而GraphCube則迅速增加。

實驗結果驗證了基于II-GC處理cuboid查詢的高效性。

3.3 crossboid查詢實驗

本小節對比II-GC和GraphCube的crossboid查詢響應時間。在不同規模網絡上的實驗結果如圖6所示。

圖6 不同規模網絡上的crossboid查詢對比

可以看出，在II-GC的crossboid查詢性能較優，且隨著網絡規模增大，GraphCube上的crossboid查詢響應時間呈直線上升，而II-GC的變化則較為平緩。實驗結果驗證了基于II-GC處理crossboid查詢的高效性。

4 結束語

基于倒排索引的多維網絡存儲模型將逐條對比的查詢操作轉換為有序集合的交并操作，在減小存儲空間的同時優化了查詢性能。在DBLP數據集上的實驗結果表明，該模型擴展性較好，查詢效率較高。當屬性值的分類個數較多時，會出現大量短倒排索引，影響查詢效率。

[1] 程學旗,沈華偉.復雜網絡的社區結構[J].復雜系統與復雜性科學,2011,8(1):57-70.

[2] 張 娜.復雜網絡社區結構劃分算法研究[D].大連:大連理工大學,2009.

[3] 陳 旭.基于社會網絡的WEB輿情系統的研究與實現[D].西安:西安電子科技大學,2010.

[4] 張蘭華.復雜網絡建模的仿真與應用研究[D].大連:大連理工大學,2013.

[5] Han Jiawei, Sun Yizhou. Mining heterogeneous information networks[C]//Proc of the 16th ACM SIGKDD international conference on knowledge discovery and data mining.[s.l.]:ACM,2013.

[6] 吳 巍.復雜網絡可視化與Link OLAP[D].北京:北京郵電大學,2007．

[7] Chen Chen, Yan Xifeng, Zhu Feida,et al. Graph OLAP:a multi-dimensional framework for graph data analysis[J].Knowledge and Information Systems,2009,21(1):41-63.

[8] Li Chuan,Zhao Lei,Tang Jie,et al.Modeling,design and implementation of graph olaping[J].Journal of Software,2011,22(2):258-268.

[9] Li Chuan,Yu P S,Zhao Lei,et al.InfoNetOLAPer:integrating InfoNetWarehouse and InfoNetCube with InfoNetOLAP[J].Proceedings of the VLDB Endowment,2011,4(12):1422-1425.

[10] Zhao Peixiang,Li Xiaolei,Xin Dong,et al.Graph cube:on warehousing and OLAP multidimensional networks[C]//Proc of ACM SIGMOD international conference on management of data.[s.1.]:ACM Press,2011:853-864.

[11] Qu Qiang,Zhu Feida,Yan Xifeng,et al.Efficient topological OLAP on information networks[C]//Proc of the 16th international conference on database systems for advanced applications.Berlin:Springer-Verlag,2011:389-403.

[12] 邵連龍,尹 沐.基于DBLP的多維異質網絡Graph Cube設計與實現[J].計算機應用研究,2014,31(3):720-724.

[13] Baeza-Yates R.Experimental analysis of a fast intersection algorithm for sorted sequences[C]//Proceedings of the 12th international conference on string processing and information retrieval.[s.l.]:[s.n.],2005:13-24.

[14] Baeza-Yates R.A fast set intersection algorithm for sorted sequences[C]//Proceedings of the 15th annual symposium on combinatorial pattern matching.[s.l.]:[s.n.],2004:400-408.

A Multi-dimensional Network Storage Model Based on Inverted Index

ZHANG Zhi-yuan，XU Heng-pan

(School of Computer Science & Technology,Civil Aviation University of China, Tianjin 300300,China)

A network such as social network linked by entities with multiple attributes is called multi-dimensional network.OLAP query on multi-dimensional network has an important application value.Most existing methods read records one by one from a file or a database.When a lot of data involved,these methods need more I/O time,thus leading to large query response time and low query efficiency.A new multi-dimensional network storage model based on inverted index is presented,called II-GC (Inverted Index based Graph Cube).It speeds up the process by constructing inverted index both on topological graph and multiple attributes.Algorithms about cuboid and crossboid are also introduced.Experimental results on DBLP show that this model is more efficient and scalable than GraphCube.

multi-dimensional network;graph cube;inverted index;OLAP

2015-07-15

2015-10-21

時間：2016-03-22

國家自然科學基金資助項目(61201414,61301245,U1233113)

張志遠(1978-)，男，副教授，碩士研究生導師，研究方向為數據挖掘；徐恒盼(1987-)，女，碩士研究生，研究方向為數據倉庫技術。

http://www.cnki.net/kcms/detail/61.1450.TP.20160322.1521.070.html

TP391.9

A

1673-629X(2016)04-0025-06

10.3969/j.issn.1673-629X.2016.04.006