遺傳算法求解電力設施選址問題

莫漢培，陳秋良，張子臻

(1.東莞供電局,廣東 東莞 523000;2.中山大學 移動信息工程學院,廣東 珠海 519000)

遺傳算法求解電力設施選址問題

莫漢培1，陳秋良2，張子臻2

(1.東莞供電局,廣東 東莞 523000;2.中山大學 移動信息工程學院,廣東 珠海 519000)

電力系統設施選址優化問題是電力系統規劃和設計中的一個基礎性問題，可以抽象成約束型的p-中位(p-median)問題，這是一個經典的NP-hard問題。該問題可以描述為從一個點的集合中選擇p個有容量限制的中位點，讓它們去服務一些有需求的點(客戶)，要求每一個中位點都不超出容量，并且總花費最小。文中針對這一優化問題，在經典遺傳算法的基礎上，提出了一種改進的遺傳算法，并混合使用局部搜索算法，進行問題的求解。該算法能夠利用遺傳算法的全局收斂性，并且有效克服遺傳算法的局部收斂和早熟問題，從而得到更準確的近似解。最后，使用網上的公開測試數據集以及經地理信息平臺(GIS)收集的某供電局的坐標信息進行實驗驗證。結果表明，提出的算法能夠有效解決設施選址問題，并且為企業提供切實可行的方案。

設施選址；遺傳算法；約束型p-中位問題；GIS平臺

1 概 述

在電力系統的規劃和設計中，確定服務設施點比如變電站的位置是非常基礎性的工作，這對于后期設備的維護、工作人員的調度都有很大影響。在實際的情形中，由于服務點數量龐大，地理位置信息相對復雜，以及人員容量等限制條件較多等原因導致該問題求解困難。

設施選址問題[1-2]是一個經典的組合優化問題，這個問題可以描述為在一片區域內有一些服務點，這些服務點都有一定的需求服務量，要從中選擇p個設施點來服務這些服務點，并且要求滿足一定的限制。文中所考慮的是約束型p-中位問題，這個問題是設施選址問題的一種常見形式，在實際生產生活中應用廣泛，并且在運籌學、組合調度等領域都有研究。約束型p-中位問題已經被證明是一個NP-hard問題，因此精確解無法在多項式時間內得到，所以人們都傾向于使用現代啟發式算法或者一些近似算法以得到問題的近似最優解。

近些年來，許多學者提出的一些解決方法都是基于啟發式算法思想的。文獻[3-5]提出了一種基于禁忌搜索的方法，主要是通過禁忌表的方法來改善局部搜索陷入局部最優解的問題；文獻[6-7]提出用模擬退火的方法解決p-median問題，同樣也是用一種退火機制來跳出局部最優解；文獻[8]采用雙層模擬退火算法，外層對設施選址決策進行優化,內層則在上層確定的設施選址決策基礎上,進行用戶需求分配的優化；文獻[9-10]使用了蟻群算法來求解；文獻[11]使用了局部搜索的方法；文獻[12-14]使用了遺傳算法來求解。隨著研究的深入，越來越多的學者傾向于改進傳統的啟發式算法并且混合使用多種方法來提高算法的性能或者減少時間復雜度。例如，文獻[15-16]使用禁忌搜索和遺傳算法混合求解這一類問題，并得到了較好的結果。

禁忌搜索、模擬退火、遺傳算法等啟發式算法可能受到待求解問題不同條件的影響，在時間、效率、精確度等方面表現出一些差異。在問題規模比較大時，以遺傳算法為代表的進化類算法以其優良的自適應性和學習性表現出比較好的性能。

文中針對約束型p中位問題，在經典遺傳算法的基礎上，提出了一種改進的遺傳算法，并混合使用局部搜索算法，進行問題的求解。

2 問題建模

文中所討論的電力系統設施選址問題將優化目標抽象為距離的花費，目標是使得服務點到設施點的距離總和最小(當然，這個目標根據不同的問題情境是可以進行修改的)。將該電力設施選址問題從現實世界中抽象出來，并用數學語言建模成約束型p-中位問題(Capacitatedp-MedianProblem，CPMP)，具體描述如下：

假設有一個無向圖G={V,E}，V為頂點，E為無向邊。假設無向圖是全連通的，即每兩個點之間都有一條邊。那么這個問題可以描述為從無向圖的頂點集合V中尋找數量為p的子集，并且滿足以下約束：

(1)

s.t.

(2)

(3)

(4)

上面的模型中出現的數學符號的含義為：

V={1,2,…,n}是所有服務點集合，同時也是候選的設施點(medians)集合；

dij是服務點i到服務點j的距離；

xij表示分配與否，xij=1表示服務點i分配到設施點j，反之xij=0表示沒有分配；

xjj表示是否被選為設施點，xjj=1表示點j被選為設施點，反之xjj=0表示沒被選；

qj表示點j的需求量；

Qj表示設施點j的容量。

式(1)是該選址問題的目標函數，即目標為最小化所有服務點(也稱客戶點，下同)到它所分配的設施點(medians)的距離總和；式(2)要求每一個服務點都分配了惟一一個設施點；式(3)表示一共選取了p個設施點；式(4)表示每一個設施點都不能超過它的容量限制。

3 遺傳算法

遺傳算法(GeneticAlgorithm)是模擬達爾文生物進化論的自然選擇和遺傳學機理的生物進化過程的計算模型，是一種通過模擬自然進化過程搜索最優解的方法，它最初由美國J.Holland教授于1975年首先提出。利用遺傳算法求解優化問題的基本思想是：把需要求解的問題模擬成一個生物進化的過程，通過復制、交叉、突變等操作產生下一代的解，并逐步淘汰掉適應度函數值低的解，增加適應度函數值高的解。這樣進化N代后就很有可能會進化出適應度函數值很高的個體，算法能夠保證求解時的收斂性。

運用遺傳算法求解組合優化問題的主要步驟為：染色體編碼，適應值計算，種群選擇，交叉，變異等。以下將結合電力設施選址問題對遺傳算法進行具體說明。

3.1 染色體編碼

染色體編碼，就是要將待求解問題的解表示成基因串的形式，這樣才能使用遺傳算法進行求解。

在電力設施選址的問題中，由于可供選址的設施點是空間離散分布的，所以采用p個設施點的索引(編號)來進行染色體的編碼。首先給所有可選擇的設施點編號(1,2,…,n)，在遺傳算法中每一條染色體有p個基因，每一個基因就是一個設施點的編號。因此，如果p=5，那么染色體gene可能表示成gene={index1，index2，…，index5}，其中index表示可供選擇的設施點的編號1,2,…,n。需要特別注意的是，這里的基因是沒有順序的，即染色體{1，3，2}和{1,2,3}是一樣的，這對于后面交叉操作時防止同一條染色體出現重復基因有很大作用。

3.2 適應值計算

遺傳算法中使用適應值來表示解得優劣，并作為后續選擇操作的依據。在大多數情況下，人們通常將目標函數映射成函數值非負的適應值函數。得到一條染色體之后，定義染色體的適應值為所有服務點到該點所分配的設施點的距離總和。首先，忽略地理環境的復雜信息，考慮兩點之間的歐氏距離。目標是最小化距離總和D，如何給所有的服務點分配一個設施點分配以達到該目標。這是一個廣義分配問題(GeneralAssignmentProblem，GAP)，也是一個NP-hard問題。長期以來，有許多方法被用來解決這一問題，例如經典的貪心算法、基于“優先級”的分配算法、拉格朗日松弛等等。

考慮到計算的復雜性和時間性能，文中采用基于優先級的貪心分配策略，它的時間復雜度不高而且效果較理想，能夠較好地解決這一問題。該算法的具體流程描述如下：

對于一個服務點c，計算它到所選取的每一個設施點的距離，然后對得到的距離值進行排序。記服務點到最近的設施點的距離為d1，到次近的設施點的距離為d2，那么服務點c的優先級為：

Priority(c)=d2-d1

首先算出所有服務點的優先級，然后按照優先級從高到低進行分配，優先級越高的優先分配設施點給它。對此，可以這樣理解，優先級越高的服務點，說明離它最近的設施點和次近的服務點相差越大，如果到后面給它分配，一旦離它最近的設施點的容量已經滿了，那么就會增加很大的花費，這是不符合需求的。因此基于這種優先級的貪心方法，可以較好地解決這個分配問題。

3.3 選 擇

選擇是遺傳算法中非常重要的一步，選擇的目的是把優化的個體(或解)直接遺傳到下一代或通過配對交叉產生新的個體再遺傳到下一代。選擇操作是建立在群體中個體的適應度評估基礎上的。計算出每條染色體的適應值之后，就可以采取一定的選擇策略來對種群進行選擇。

常用的選擇策略有輪盤賭選擇、錦標賽選擇等等，這些選擇方法都有一定的優缺點。為了防止種群過早陷入局部收斂，同時避免種群的退化，沒有采用輪盤賭的選擇方法，因為輪盤賭選擇很快就會出現大量相同的染色體，從而陷入局部解。

文中采取了一種根據適應值排序的混合選擇策略：首先，計算每一條染色體的適應值，并且按照適應值從高到低進行排序；然后，按照適應值進行選擇，適應值高的選擇保留到后代，在這個過程中需要保證不出現重復的染色體。同時，保留很小比例的最差解，有利于防止局部收斂。

3.4 交 叉

類似于自然界生物進化過程，基因的交叉互換和重組能夠產生新的個體，在遺傳算法中，通過交叉操作，將大大提高遺傳算法的搜索能力，加速求解過程，并期望優秀的基因結合在一起，從而得到更優解。

例如，c={1,2,3,4,5,6}是最優解，而已經得到c1={8,9,3,4,5,6}和c2={1,2,6,7,10,11}，那么按照如下的交叉方式進行基因重組：

具體來說，根據前面所述的染色體編碼方法，將采用如下的交叉算法：

(1)預處理。因為每個設施點只能出現一次，所以要保證在經過交叉之后一條染色體中不會出現兩個相同的基因。預處理的方法是：對于參與交叉的兩條染色體，計算出染色體相同的部分移到染色體的右邊，并將不同的部分移到左邊。

(2)當兩條染色體不完全相同的時候，進行交叉運算，可以采用經典的單點交叉。

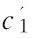
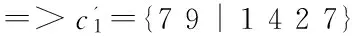
而經過預處理，兩條染色體變為：

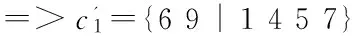
經過交叉互換得到的新的染色體符合要求。

(3)如果兩條染色體完全相同，為了防止陷入局部最優解，采用的方法是引入新的染色體，即隨機生成一條新的染色體，并與之另一條進行交換。

3.5 變 異

變異操作是模擬自然界遺傳過程中的基因突變，需要注意的是，基于突變是隨機發生的，而且概率較低。

遺傳算法引入變異操作的主要作用有兩個：一是使遺傳算法具有局部的隨機搜索能力。當遺傳算法通過交叉算子已接近最優解鄰域時，利用變異操作的這種局部隨機搜索能力可以加速向最優解收斂。顯然，此種情況下的變異概率應取很小的值，否則接近最優解的狀態會因變異而遭到破壞。二是使遺傳算法可維持群體多樣性，以防止程序出現早熟收斂現象，得不到理想的近似解。

在變異操作中，隨機地對染色體的某一個基因進行變異，把這個基因隨機替換成另外一個沒有出現在染色體中的基因，即服務點的編號。在這個過程中，可以保證一條染色體中不會出現兩個相同的基因。比如將c1={2 8 1 4 5 7}進行變異操作，可能得到的結果為：

其中，c1染色體的第5個基因從5變異為3。

3.6 局部搜索

樸素的遺傳算法在求解時，需要非常多的迭代次數，才能得到比較好的近似解。為了提高遺傳算法的搜索能力，加快收斂速度，減少程序的運行時間復雜度，引入了局部搜索策略。

在完成交叉和變異之后，以一定的比例選取部分染色體進行局部搜索，尋找在這個解得鄰域中的更優解。具體的算法流程如下：

首先，對于所選中的染色體的每一個基因c，搜索距離它最近的k個服務點。其中k是一個經驗值，k越大，時間復雜度越高，但是k越小，搜索的范圍小，優化效果可能也比較小。因為這里是需要做一些局部的優化，所以k盡量選擇較小一些，在實驗過程中需要調節k值。

然后，把c替換成它鄰近的服務點，如果能夠得到更優的適應值，則替換它。同樣的，這里也需要保證染色體中不出現相同的基因。

經過局部搜索，可以讓部分解加速向最優解靠攏，從而加快算法的收斂速度。

4 實驗分析

文中利用C++實現了前面描述的算法并進行了實驗分析。實驗機器的配置為：CPUInteli5 主頻2.3GHz，內存8G。

為了驗證算法的正確性和有效性，文中采用了兩個數據集進行測試和驗證。第一個數據集是來自網絡上著名的優化問題公開測試數據集—OR-Library(http://people.brunel.ac.uk/～mastjjb/jeb/info.html)。選取了OR-Library中的p-median-capacitated問題的測試數據，測試程序選取其中的10個測試用例，其中5組服務點數量n為50，設施點數目p為5，另外5組服務點數量n為100，設施點數目p為10。

測試結果如表1所示。

表1 第一個數據集上的測試結果

分析測試結果發現,使用文中改進的遺傳算法可以有效解決約束型p中位問題。隨著服務點和設施點數量的增加，運行的時間也在增加。在運行時間不超過30s的情況下，算法最好的結果誤差為2.6%，最壞的結果誤差為5.5%。

為了更直觀地顯示程序運行的結果，將其中一組數據的服務點和經過文中算法求解出的設施點畫在圖上，如圖1所示。

第二個數據集來源于GIS平臺收集的數據。該平臺是基于高德地圖針對某供電局的裝置設備坐標定位而開發的。通過該平臺，獲得了這些客戶點的地理信息數據。針對這些數據，對電力設施進行選址，對不同

圖1 表1中一組數據，設施點選擇和分配結果

的設施點數量p進行實驗，結果如表2所示。

表2 利用某供電局裝置數據測算結果

5 結束語

文中給出了利用改進的遺傳算法解決電力系統設施選址問題的一種實現方法，并且與網上公開測試數據集進行對比，驗證了算法的可行性；同時該算法也表現出了良好的時間性能。此外，通過GIS系統收集了某供電局的電力設施數據并使用該方法進行求解，能得出較滿意的結果。

當然，在實驗過程中發現，提出的算法處理約束型p中位問題時，對于不同的問題規模和數據表現出了一定的效果差異，這說明對于算法在不同情況的性能的穩定性方面還需更深入的工作，加以改進和優化。

[1] 王 非,徐 渝,李毅學.離散設施選址問題研究綜述[J].運籌與管理,2006,15(5):64-69.

[2] 楊豐梅,華國偉,鄧 猛,等.選址問題研究的若干進展[J].運籌與管理,2005,14(6):1-7.

[3]RollandE,SchillingDA,CurrentJR.Anefficienttabusearchprocedureforthep-medianproblem[J].EuropeanJournalofOperationalResearch,1997,96(2):329-342.

[4]GloverF.Tabusearch-partI[J].ORSAJournalonComputing,1989,1(3):190-206.

[5] 郭崇慧,覃華勤.一種改進的禁忌搜索算法及其在選址問題中的應用[J].運籌與管理,2008,17(1):18-23.

[6]MurrayAT,ChurchRL.Applyingsimulatedannealingtolocation-planningmodels[J].JournalofHeuristics,1996,2(1):31-53.

[7]ChiyoshiF,Galv?oRD.Astatisticalanalysisofsimulatedannealingappliedtothep-medianproblem[J].AnnalsofOperationsResearch,2000,96(1-4):61-74.

[8] 秦 進,史 峰.物流設施選址問題的雙層模擬退火算法[J].系統工程,2007,25(2):36-40.

[9] 許 婷,盛 明,婁彩榮.基于GIS和蟻群算法的物流配送中心選址研究[J].測繪科學,2010,35(6):206-208.

[10] 李有梅,陳 曄.一種新的求解約束P-中位問題的啟發式算法[J].計算機工程,2005,31(19):162-164.

[11]LorenaLAN,SenneELF.Localsearchheuristicsforcapacitatedp-medianproblems[J].NetworksandSpatialEconomics,2003,3(4):407-419.

[12]Estivill-CastroV,Torres-VelázquezR.Hybridgeneticalgorithmforsolvingthep-medianproblem[M]//Simulatedevolutionandlearning.Berlin:Springer,1999:18-25.

[13]AlpO,ErkutE,DreznerZ.Anefficientgeneticalgorithmforthep-medianproblem[J].AnnalsofOperationsResearch,2003,122(1-4):21-42.

[14]GhoseiriK,GhannadpourSF.Solvingcapacitatedp-medianproblemusinggeneticalgorithm[C]//ProcofIEEEinternationalconferenceonindustrialengineeringandengineeringmanagement.[s.l.]:IEEE,2007:885-889.

[15]GloverF,KellyJP,LagunaM.Geneticalgorithmsandtabusearch:hybridsforoptimization[J].Computers&OperationsResearch,1995,22(93):111-134.

[16] 李大衛,王 莉,王夢光.遺傳算法與禁忌搜索算法的混合策略[J].系統工程學報,1998,13(3):28-34.

Solving Grid System Facility Location Problem Based on Improved Genetic Algorithm

MO Han-pei1，CHEN Qiu-liang2，ZHANG Zi-zhen2

(1.Power Grid Co.,Guangdong Dongguan Power Supply Bureau,Dongguan 523000,China;2.School of Mobile Information Engineering,Sun Yat-Sen University,Zhuhai 519000,China)

Grid system facility location,as a basic problem in grid system plan and design,can be modeled as a capacitatedp-medianproblem,whichisaclassicalNP-hardproblem.Itcanbedescribedasselectingp-capacitatedmediansfromaverticessetinordertoserveasetofdemandvertices(customers),sothatthetotalassigneddemandtoeachofthecandidatemediandoesnotexceeditscapacity,andthecostisminimum.Tosolvethisproblem,animprovedgeneticalgorithmincorporatedwithalocalsearchprocedureisproposedbasedonclassicalgeneticalgorithm.Itcanusetheglobalconvergenceandavoidthelocalconvergenceandprematureingeneticalgorithmtoobtainthemoreaccurateapproximatedsolution.Thealgorithmhasbeentestedusingstandardtestingdataandtherealdatacollectedbyageographicinformationsystem.Theresultsshowthatthismethodcanprovideafeasibleandpromisingsolutionfortheindustry.

facility location;genetic algorithm;capacitatedp-medianproblem;NP-hard;GISplatform

2015-01-06

2015-04-10

時間：2016-02-18

中央高校基本科研業務費專項資金(15lgpy37)

莫漢培(1967-)，男，助理工程師，主要從事電力系統管理工作。

http://www.cnki.net/kcms/detail/61.1450.TP.20160218.1619.014.html

TP

A

1673-629X(2016)03-0197-05

10.3969/j.issn.1673-629X.2016.03.046