基于LINGO的傳動軸多目標可靠性優化設計

王俊

（中冶華天工程技術有限公司，江蘇南京210019）

基于LINGO的傳動軸多目標可靠性優化設計

王俊

（中冶華天工程技術有限公司，江蘇南京210019）

本文以移鋼鏈傳動軸為優化設計目標，引入可靠性設計原理，建立以傳動軸截面積和外徑最小為目標函數的數學模型，利用LINGO軟件編程優化，求解目標函數最優解。結果表明，利用LINGO求解多目標優化問題，能得到較好的優化結果，算法簡單，數據可靠。

LINGO；可靠性；多目標優化；傳動軸

在機械設計過程中，常規設計經常使用的是基于安全系數的設計，而在設計中許多物理量是隨機變量，也就是說在常規設計時，代入的變量只是隨機變量中的一個樣本值，那么仍然存在不安全、失效的可能性。若在常規設計中引入概率設計，這樣將會使設計結果更加符合實際，并能定量地給出機械零件或機構不失效的概率，即可靠度。

多目標優化是現代設計方法中重要部分，可以將多目標優化設計延伸到數學中的多目標規劃問題上，即將設計中的物理模型轉化為數學模型，根據設計所追求的性能目標，建立目標函數，選取合適的設計變量，在滿足給定的各種約束條件下，尋求最優化設計方案和最佳設計參數。通常情況下，將多目標優化根據目標函數的重要性進行加權運算構造一個綜合的評價函數，即轉為單目標優化來解決問題。本文將通過LINGO軟件包來對傳動軸多目標可靠性優化設計進行求解。

1 LINGO模型形式

LINGO是求解運籌學、數學建模的常規軟件，可以快速、有效地求解線性、非線性規劃模型問題，功能強大，操作簡潔，無需編制大量程序，易輸入，用戶界面良好。使用LINGO軟件求解多目標優化時，需將多目標轉為單目標問題。LINGO模型同樣是由設計變量、目標函數和約束條件組成。

其多目標優化轉為單目標模型基本形式如下：

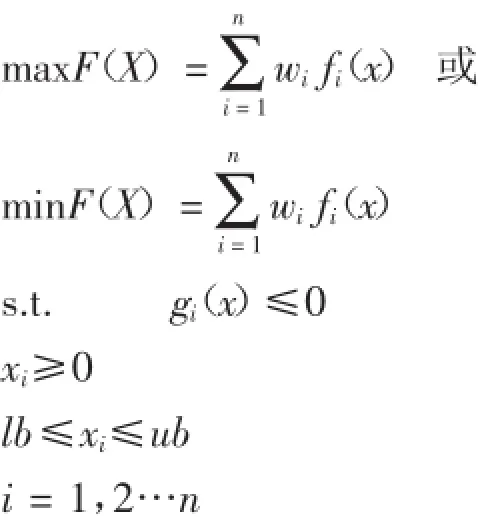
式中，wi為加權因子；lb，ub為矢量；F（X），fi（x），gi（x）可為線性函數，也可為非線性函數。

2建立優化設計數學模型

2.1 初始條件

某軋鋼廠精整區移鋼鏈傳動軸設計，結構形式如圖1所示。已知參數為：軸長L為定值，軸的材料選用45#鋼，剪切彈性模量G=81 GPa，許用剪切應力[子]＝45 MPa，每米長的允許扭轉角為[φ]＝1°/m.軸所傳遞的功率為11 kW，轉速為58 r/min，需確定傳動軸可靠度達到0.999 9時的優化設計參數。

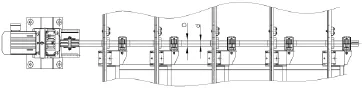
圖1 移鋼鏈結構示意圖

2.2 設計變量選取

對于傳動軸而言，在長度一定的條件下，傳動軸的體積僅與軸徑有關，這樣可以采用軸徑作為設計變量，即外徑D，內徑d，若d=0時，為實心軸。則：

2.3 目標函數的建立

要建立好目標函數，首先要明確優化設計的要求，即在滿足可靠度以及其它約束條件的基礎上，使得傳動軸的體積最小，上文提到軸長是定值，那么性能目標就應調整為軸的截面積最小，軸的外徑最小。

由上述要求，目標函數可建立如下：

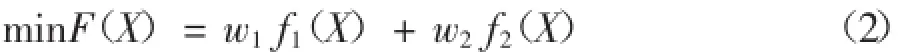
其中：

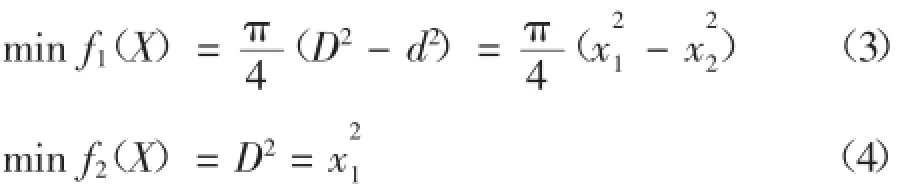
式中：w1，w2為分目標函數權重，可根據設計經驗，分目標函數的重要程度判斷給出。

2.4 約束條件

由于傳動軸只受扭矩，不受彎矩或彎矩很小，可不參與計算，應按照扭轉強度進行設計。（1）扭轉強度條件約束按照扭轉強度要求，則：

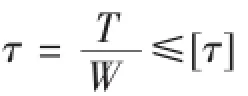
演算后得：

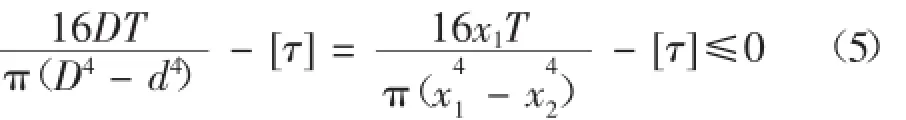
式中：

τ為扭轉切應力（MPa）；T為軸所受扭矩（N· mm）；W為軸的抗扭截面系數（mm3）；[τ]為許用扭轉切應力（MPa）.

（2）扭轉強度可靠性約束

根據可靠性設計應力-強度干涉模型以及軸需達到可靠度要求，得出：

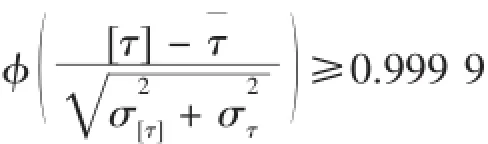
通過查正態分布表得：

式中：τˉ為工作扭轉切應力均值（MPa）；στ為工作扭轉切應力標準差；[τ]為許用扭轉切應力（MPa）；σ[τ]為許用扭轉切應力標準差。

考慮許用扭轉切應力為定值，則σ[τ]＝0.

根據3σ原則以及軸徑制造公差統計數據列出軸徑的標準差：

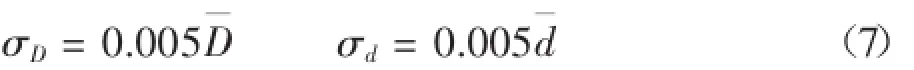
現需計算出工作扭轉切應力均值及其標準差στ.

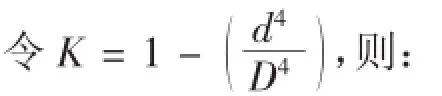
抗扭截面系數：

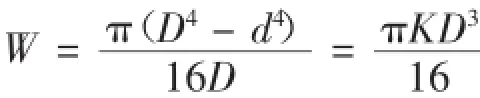
抗扭截面系數均值：

抗扭截面系數標準差：

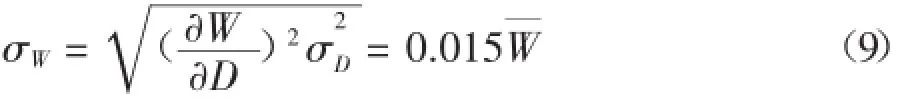
扭轉切應力均值：

扭轉切應力標準差：

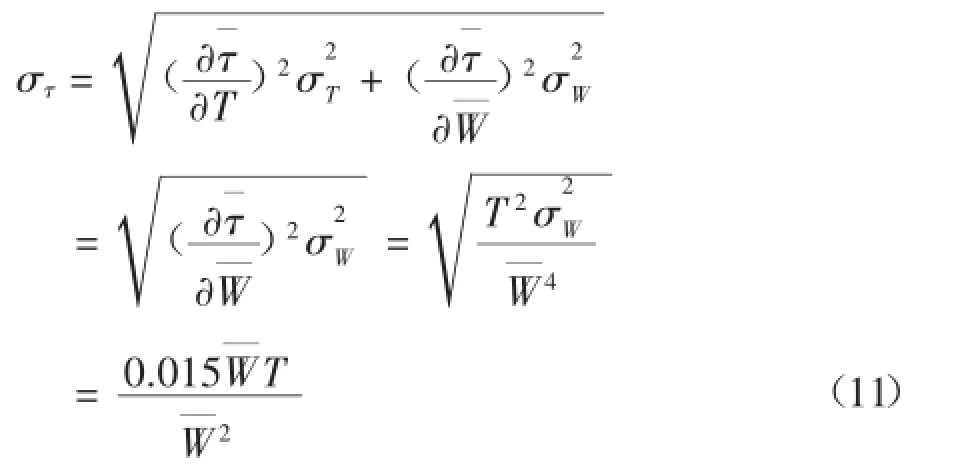
聯立式（6），（7），（8），（9），（10），（11）得：

（3）扭轉剛度條件約束

軸的扭轉變形是用每米長的扭轉角來表示，即：

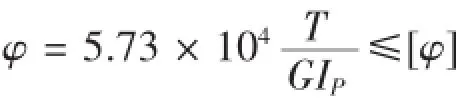
經演算后得：

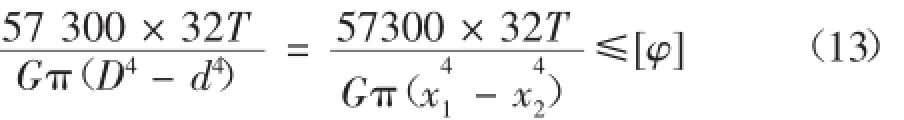
式中：φ為工作扭轉扭轉角；IP為軸截面的極慣性矩，IP＝π（D4-d4）/32；[φ]為每米允許扭轉角；G為軸的材料的剪切彈性模量。

（4）其余約束條件

考慮數值的非負性，以及軸的外徑大于內徑，即：

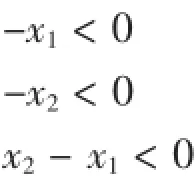
綜上所述得出總體的數學模型如下：

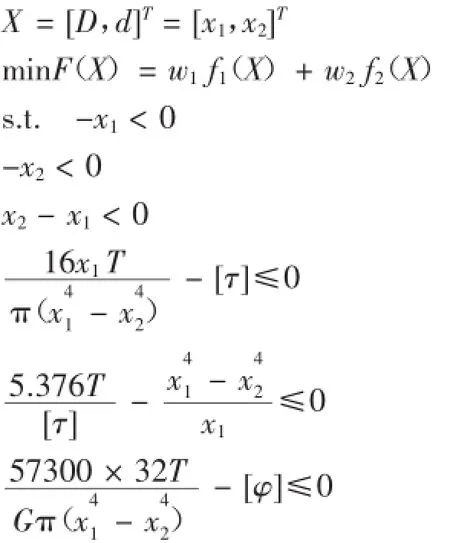
3優化設計程序與分析

3.1 LINGO程序編制

根據數學模型編寫LINGO源程序如下：

model：

Title Nonlinear Programing;

data：

weight1=0.4；!定義分目標函數權重；

weight2=0.6；!定義分目標函數權重；

enddata

init：

x1=80；!設置初始值；

x2=0;

endinit

min=weight1*0.78539*（x1^2-x2^2）

+weight2*x1^2；!目標函數;

@bnd（0，x1，170）；!定義上下限約束條件；

@bnd（0，x2，100）；

-x1+x2≤0；

-x2≤0；

（9224400*x1/（x1^4-x2^4））-45≤0；

（13050819/（x1^4-x2^4））-1≤0；

216379-（x1^4-x2^4）/x1≤0；

end

通過運算得出如下結果：

Global optimal solution found.

Objective value：3143.708

Objective bound：3143.705

Infeasibiliwties：0.2910383E-10

Extended solver steps：10

Total solver iterations：617

Model Title：Nonlinear Programing

Variable Value Reduced Cost

WEIGHT1 0.400 000 0 0.000 000

WEIGHT2 0.600 000 0 0.000 000

X1 61.495 06 0.000 000

X2 31.579 84 0.000 000

即經過617次迭代計算，找到全局最優解，x1=61.495 06，x2=31.579 84；考慮有一側鍵槽，軸徑增大3%，經圓整后得x1=64，x2=32；若采用實心軸，通過上述程序運算得出：x1=60.104 84，x2=0.經圓整后得x1=62，x2=0.

3.2 優化設計結果及分析

優化前后數據對比如表1所示。通過數據對比，優化后的傳動軸在滿足0.9999的可靠度下，軸徑下降了20%，在軸長定值情況下，重量下降了40%～50%，優化結果優于原設計結果。

4結束語

優化設計后的設計結果相對原設計，降低了制造加工成本，有一定的經濟效益，如表1所示。

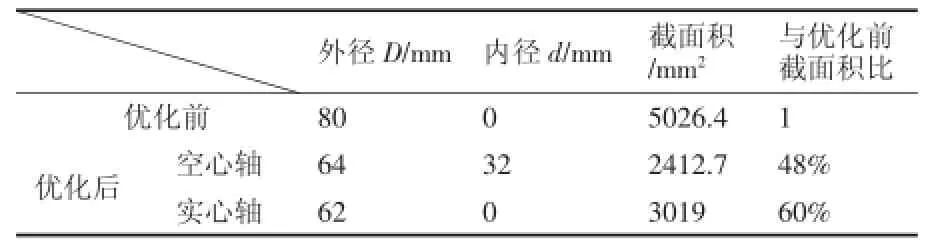
表1 優化前后數據對比

由于現實中的設計變量大都是隨機變量，呈現一定的離散性，所以引入可靠性設計，能使設計結果更符合實際，有重要的現實意義。

運用LINGO模型算法優化計算，操作簡單，易于輸入，設計人員不需要編寫大量繁瑣復雜的算法程序，同樣能得到合理的優化設計參數，大大提高了設計效率，對設計工作具有一定的指導意義。

[1]盧玉明.機械零件的可靠性設計[M].北京：高等教育出版社，1989.

[2]濮良貴，紀名剛.機械設計[M].7版.北京：高等教育出版社，2001.

[3]謝金星，薛毅.優化建模與LINDO/LINGO軟件[M].北京：清華大學出版社，2005.

[4]張鄂.現代設計方法[M].北京：高等教育出版社，2013.

[5]陳志華，劉世峰，董朝盼.傳動軸多目標可靠性優化設計[J].煤礦機械，2014，35（11）：26-28.

MultiObjective Reliability Optim ization Design of Transm ission Shaft Based on LINGO Language

WANG Jun
（Huatian Engineering&Technology Corporation，MCC.Nanjing Jiangsu 210019，China）

This paper takes the transmission shaft ofmoving steel chain as the optimization design objective，and drawing into the reliability design principle，the mathematical model with the objective of minimizing of the sectional area and outer diameter of the transmission shaft is established，and using lingo software programming optimization to solve the optimal solution of the objective function.The result shows that the optimization results can be obtained by using LINGO to solve multi-objective optimization problems，the algorithm is simple and the data is reliable.

TH122

A

1672-545X（2016）12-0017-04

2016-09-29

王俊（1984-），男，安徽和縣人，工程師，碩士研究生，研究方向：冶金機械設計與研發。

Key w rods：LINGO；reliability；multi objective optimization；transmission shaft