軌道坐標系到地心固定坐標系的直接轉換方法

竇長勇岳昔娟

（1 中國科學院 電子學研究所，北京 100090）

（2 中國科學院大學，北京100049）

（3 中國科學院 遙感與數字地球研究所，北京100094）

軌道坐標系到地心固定坐標系的直接轉換方法

竇長勇1,2,3岳昔娟3

（1 中國科學院 電子學研究所，北京 100090）

（2 中國科學院大學，北京100049）

（3 中國科學院 遙感與數字地球研究所，北京100094）

坐標系轉換是實現應用導航數據進行衛星遙感影像高精度定位的關鍵技術。文章利用航天器定義在地心固定坐標系下位置和速度信息，應用四元數（Quaternion）方法，實現從航天器軌道坐標系到地心固定坐標系的直接轉換。在常規遙感影像直接定位算法中這樣的轉換分為兩次坐標系旋轉，先從軌道到地心慣性，然后從地心慣性到地心固定坐標系。文中提出的方法將這兩次坐標系轉換縮減為一個，并且避免了應用地球的章動、極移和歲差等信息。通過跟傳統坐標系轉換方法轉換結果以及商業軟件STK (Satellite Tool Kit)定位結果的比較，證明了該方法的正確性和實用性，適合于低軌對地觀測平臺的遙感影像定位，因為低軌平臺提供了定義在地心固定坐標系下的位置和速度信息。

坐標系轉換 四元數 軌道坐標系 地心固定坐標系 空間向量旋轉 遙感應用

Key wordscoordinate system transformation; quaternion; spacecraft orbital reference frame; Earth-centered and Earth-fixed reference frame; rotation of space vector; remote sensing applications

0 引言

作為遙感應用的關鍵技術，遙感影像地理定位是獲取高品質的遙感和測繪產品的基礎。定位算法就是建立傳感器成像陣列像素點（像方坐標）和所觀測目標（物方空間位置）的聯系，遙感影像定位是測繪制圖和遙感應用研究的必要數據處理環節[1-2]，坐標系轉換是應用導航數據進行遙感影像定位的必經步驟。星載遙感影像正向地理定位算法中常用的坐標系統依次為：傳感器自身坐標系→遙感平臺本體坐標系→軌道坐標系→地心慣性坐標系→地心固定坐標系，在地心固定坐標系下進行傳感器視線向量和地球表面交點的求解[3]。其中，從軌道坐標系到地心慣性坐標系要用到在地心慣性坐標系下定義的遙感平臺的位置和速度信息，從地心慣性坐標系到地心固定坐標系要用到地球的章動、極移和歲差等信息。章動、極移和歲差等被稱作為地球的方位信息，它們隨時間變化，“國際地球自轉和參考系服務”（International Earth Rotation and Reference Systems Service，IERS）提供了比較權威的實時數據，然而，在遙感影像正向直接定位算法過程中要獲取實時的地球方位信息比較麻煩。

國內外學者在遙感影像定位方面進行了比較深入的研究[4-8]，新的技術方法也在不斷發展，四元數（Quaternion）方法就是其中一種比較新的技術。四元數是高效的空間向量方位表示及旋轉操作的工具，近年來被應用于遙感影像定位方面并取得了較好的效果。文獻[9]提出了適用于線陣影像的空間后方交會的四元數方法；文獻[10]提出了無初值依賴的空間后方交會；文獻[11-12]提出了對偶四元數的線陣遙感影像幾何定位方法，并把它應用于相對定向的表示；文獻[13]對基于單位四元素的依初值和無初值空間后方交會進行了研究。這些方法都是應用四元數方法來研究傳感器構像方程的解算，而四元數在坐標系轉換方面的優勢還沒有涉及。坐標系轉換是應用導航定位數據確定遙感影像方位信息的關鍵步驟[14-15]，當航天器在較低的軌道運行時，衛星導航數據可以直接提供其在地心固定坐標系的位置與速度信息。本文利用此信息，應用四元數方法實現從遙感器軌道坐標系到地心固定坐標系的直接轉換。在常規的遙感影像直接定位算法中這樣的轉換首先從軌道到地心慣性，然后從地心慣性到地心固定坐標系。本文方法將這兩次轉換縮減為一個，為直接定位算法提供了一種新的坐標系轉換方法，也擴展了四元數方法應用領域。

1 傳統坐標系統轉換方法

1.1 坐標系統定義

本文主要針對從航天器軌道坐標系到地心固定坐標系的坐標系轉換方法，所涉及的坐標系有三個：航天器軌道坐標系、地心慣性坐標系和地心固定坐標系，見圖1。

航天器軌道坐標系（Spacecraft Orbital Coordinate System，SOCS，簡化為Orb）的原點在航天器的質心，ZOrb軸從坐標原點指向地球的質心，YOrb軸是 ZOrb軸和航天器瞬時速度的叉乘積，其方向和航天器的瞬時角動量矢量反向。XOrb軸是YOrb軸和ZOrb的叉乘積，本文中的坐標系統都是遵從右手法則的笛卡爾坐標系統。

地心慣性坐標系（Earth Centered Inertial Coordinate System，ECICS，簡化為ECI）是一空間固定的坐標系，其原點在地球的質心，它的ZECI軸從原點指向J2000的平均北天極點，XECI軸從原點指向J2000的平均春分點，YECI軸是ZECI和XECI的叉乘積。

地心固定坐標系（Earth Centered Earth Fixed Coordinate System，ECEFCS，簡化為ECEF）隨著地球旋轉而旋轉，同時還考慮極移、章動和歲差等地球的方位參量，但是此坐標系統把地球當成理想球體，不考慮其橢球的因素。地心固定坐標系的原點在地球的質心，其 ZECEF軸從坐標原點指向平均北極點，又稱國際參考極點，XECEF軸從原點指向本初子午線和赤道的交點，YECEF軸是ZECEF軸和XECEF軸的叉乘積。

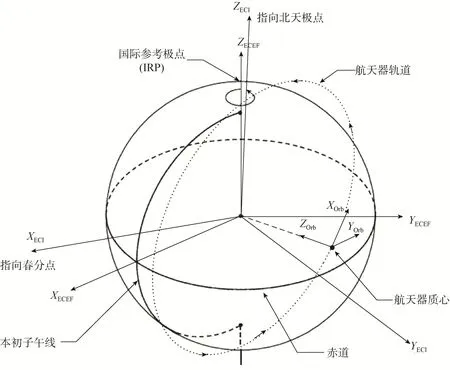
圖1 航天器Orb、ECI、ECEF坐標系示意Fig.1 The illustration of the spacecraft Orb, ECI, ECEF coordinate systems.

1.2傳統坐標系統轉換

從軌道坐標系到地心固定坐標系的常規方法分為兩個步驟：一是從軌道坐標系到地心慣性坐標系的轉換；二是從地心慣性坐標系到地心固定坐標系的轉換。在步驟一中需要定義在地心慣性坐標系統下航天器的位置和速度矢量，步驟二則需要恒星時間以及地球的極移、章動和歲差等地球的方位參量[16]。

步驟一：從航天器軌道坐標系到地心慣性坐標系的轉換

式中的b1，b2和b3由下式求得

式中 PECI和VECI是航天器在地心慣性坐標系下的位置和速度信息。步驟二：從地心慣性坐標系到地心固定坐標系的轉換

式中 Q(t)、R(t)和W(t)分別為地球的章動和歲差、自轉、極移的旋轉矩陣，具體的旋轉矩陣比較繁瑣，詳細信息在WGS84的文檔中有詳細描述[17]，此處不再贅述。

從地心慣性坐標系到地心固定坐標系轉換，不僅要考慮地球自轉還要考慮變化較慢的地球方位信息，如極移、章動和歲差信息。

傳統的從軌道坐標系到地心慣性坐標系的轉換需要定義在地心慣性坐標系下的航天器的位置和速度信息。從地心慣性坐標系到地心固定坐標系的轉換需要地球的極移、章動和歲差等地球的方位信息。由于地球的方位信息動態變化，它的信息需要實時地到國際地球自轉和參考系服務網站（http://www.iers.org）獲取，這給實際的星載遙感影像的定位帶了很多不便。

2 基于四元數坐標系轉化方法

2.1四元數簡述

四元數由愛爾蘭數學家漢密爾頓發明，它可以用四維的數據形式來表示三維的空間向量。四元數由實部和虛部組成，可表示為，其中r為實部，為虛部，它的三個虛部遵循漢密爾頓定律[18]

四元數可用四維的數據形式表示三維的空間向量，所以在三維空間向量的旋轉操作時要比傳統的歐拉角和旋轉矩陣等有一定的優勢。四元數可以追蹤旋轉的過程，因此，在空間向量多次旋轉的疊加方面有獨特的優勢。例如，四元數方法可以避免在旋轉過程中出現萬向節死鎖現象。另外，四元數可以表示空間任意向量繞任意軸旋轉，而且可以把多次這樣的旋轉疊加到一起，這對于旋轉矩陣操作就比較困難。假如空間中的任意向量vin，它可以表示為純四元數形式，它繞著空間任意軸旋轉任意角度θ，可用四元數表示為[19]

此處，vout為經過旋轉操作后的輸出向量。這里四元數是單位四元數，其定義形式為

如果把一個向量連續旋轉兩次，設表示第一次和第二次旋轉的四元數分別為q1和q2，則兩次旋轉的組合可表示為

2.2轉換方法

本文應用定義在地心固定坐標系下的航天器的位置和速度矢量信息，建立航天器軌道坐標系和地心固定坐標系的聯系。遵從坐標系轉換的本質，即是繞著坐標軸的旋轉和坐標原點的平移，利用四元數實現從軌道坐標系到地心固定坐標系的轉換。

假設某一時刻航天器在地心固定坐標系下的位置和速度分別為PECEF和VECEF，根據1.1中的坐標系定義，航天器軌道坐標系的三個軸在地心固定坐標系下表示為

坐標系轉換的本質即是繞著被轉換坐標系的三個軸分別旋轉使其和目標坐標系的三個軸方向一致，然后再平移坐標系原點使其和目標坐標系原點重合。現在就把式（9）建立的航天器軌道坐標系旋轉，使其和地心固定坐標系方向一致，因為航天器的軌道坐標系在地心固定坐標系下表示出來，兩個坐標系位于同一個坐標系統下，因此，可以按照上述坐標系旋轉的本質進行轉換。本文中地心固定坐標系的XECEF、YECEF和ZECEF軸分別表示為(1,0,0)、(0,1,0)和(0,0,1)。第一個旋轉是繞著ZOrb軸旋轉γ角度，使XOrb位于由XECEF和ZOrb決定的平面內，旋轉角度可表示為

式中 XECEF×ZOrb是XECEF和ZOrb決定的平面的法向量。因為YOrb和XOrb垂直，如果YOrb和上述平面的法向量指向相同就能保證XOrb位于由XECEF和ZOrb決定的平面內。

式（10）計算出的角度范圍是0～π，因為四元數的旋轉遵循右手法則，其范圍應該是0～2π。為了準確獲取旋轉角度，我們定義以下規則，把開始旋轉的向量稱之為Vbegin，終了向量為Vend，旋轉軸為Raxis，如果則旋轉角度范圍是0～π，否則，就是π～2π。求得旋轉角度γ，則由式（7）得出表示繞著ZOrb旋轉的四元數

式中 Zx、Zy和Zz是ZOrb的三個軸的分量。

根據式（6），分別旋轉軌道坐標系的XOrb和YOrb軸，實現軌道坐標系轉換過程中的第一次旋轉

式中 XOrb_γ和YOrb_γ是第一次旋轉后的坐標軸。

第二次旋轉是繞著經過第一次旋轉后的YOrb_γ軸旋轉，使同樣經過第一次旋轉后的XOrb_γ軸跟XECEF方向一致，這次的旋轉角度是。同理表示旋轉的四元數為

式中 Y_γx，Y_γy，Y_γz分別是YOrb_γ軸的三個分量，同樣，對 XOrb_γ和ZOrb進行旋轉，實現軌道坐標系的第二次旋轉

式中 XOrb_γβ和 ZOrb_β是第二次旋轉后的坐標軸。

第三次旋轉是繞著 XOrb_γβ軸旋轉 α角度使ZOrb_β軸和ZECEF軸方向一致。本次旋轉角度為，同理旋轉四元數可表示為

式中的三個分量是 XOrb_γβ軸的。同理，把另外兩個軸旋轉，實現軌道坐標系的第三次旋轉

經過這三次旋轉軌道坐標系和地心固定坐標系的方向就完全一致了，最后一步就是把軌道坐標系的原點移到跟地心固定坐標系重合位置，綜上所描述及根據式（8），可以得出兩個坐標系間的轉換關系為

式中 VOrb和VECEF分別是定義在軌道和地心固定坐標系下的向量。式中由三個四元數構成的旋轉表示坐標系方向上的轉換，也即是角元素，后者表示坐標原點的平移，即直線元素。

本文所提出的方法適用于已經提供了定義在地心固定坐標系下的低軌航天器位置和速度信息的情形，這樣利用位置和速度信息建立軌道坐標系和地心固定坐標系的聯系，遵從坐標系轉換的本質實現從軌道坐標系到地心固定坐標系的直接轉換。本方法的優點為把常規的兩次坐標系轉換縮減為一次，避免了應用地球的方位信息，這些信息比較難獲取。

3 驗證與比較

本文采用國際空間站的軌道數據來驗證所提出方法的正確性，因為國際空間站是低軌運行的航天器，其軌道數據同時提供了定義在地心慣性坐標系（J2000）和地心固定坐標系下的位置和速度信息。應用同一時刻的國際空間站的軌道數據，分別用傳統算法（式（1）和式（2）所描述的兩次坐標系轉換）和本文提出的算法進行比較，即可驗證本文方法的正確性。如表1所示，選用2011年第一天國際空間站一個軌道周期（其軌道周期約為 90min）中的 4個時刻的數據點進行驗證。4個時刻的分別是2011:001:00:10:00（年：天：時：分：秒）、2011:001:00:30:00、2011:001:00:42:00和2011:001:00:58:00。假設定義在軌道坐標系下的向量值為 VOrb=(3,4,5)，分別用本文所提出的方法和1.2中所介紹的傳統方法進行向量轉換。為了保證向量輸出值的比較精度，只進行角元素的轉換，本文提出的坐標系轉換方法式（17）可簡化為

這兩種方法輸入的被轉換向量都是 VOrb=(3,4,5)，它是任意定義的向量，沒有實際的單位和含義，僅起到提供兩種方法的統一輸入量的作用。輸出的向量為VECEF，用以對兩種轉換方法做對比。表1列出了上述4個時刻的輸入參數和轉換后輸出的結果比較。對于本文方法輸入的位置和速度信息定義在地心固定坐標系下，而常規方法的輸入位置和速度信息是定義在J2000坐標系下。由表1可知同樣的輸入向量應用兩種方法轉換后結果的三個分量差別非常小，在10-5級別或者更小，可以忽略不計。對比結果說明了本文方法和傳統方法對于具有同樣的旋轉效果，證明了其正確性。

為了進一步驗證，我們把本文中的坐標系轉換方法應用到遙感影像定位算法中，算法過程在文獻[16]中有詳細描述，利用改進的定位算法，把表1中4個時刻所列的參量和對應時刻的姿態信息作為輸入，計算國際空間站瞬時星下點的地理定位結果，并跟商業軟件STK（Satellite Tool Kits）的模擬結果進行了對比。本文提出算法輸入參數包括定義在地心固定坐標系下航天器的位置和速度信息（表 1）以及航天器的姿態信息（表2），STK軟件的輸入參數包括相同時刻定義在慣性坐標系下航天器的位置和速度信息（表1）以及姿態信息（表2）。從表2的比較結果可以看出，兩種方法對應的定位結果在經度和緯度上的差異都在0.5m以內，有的接近于零。考慮到定位算法中的固有誤差，這樣的定位精度進一步證明了本文方法的正確性。

表2 本文提出方法應用到定位算法中和商業軟件STK定位結果的比較Tab.2 The comparison of the geolocation results between the method proposed in this paper and STK.

4 結束語

本方法利用定義在地心固定坐標系下的航天器位置和速度信息建立軌道坐標系和地心固定坐標系之間的聯系，遵循坐標系轉換的本質，分別繞航天器軌道坐標系的三個軸旋轉，以及坐標原點的平移，實現兩個坐標系統間的直接轉換，從而把傳統方法的兩個坐標轉換縮減為一個，且避免了應用地球的章動、極移和歲差等信息。利用四元數可對空間任意向量繞任意軸進行旋轉操作的特性，求解了坐標系三次旋轉的角度，并用四元數表示了旋轉操作。應用國際空間站的軌道數據，對本文方法的正確性進行了驗證。選取2011年第一天“國際空間站”一個軌道周期中的4個時刻的軌道數據，應用本文提出的方法和傳統的坐標系轉換方法對定義在軌道坐標系下的同一向量分別轉換到地心固定坐標系下，轉換后向量的三個分量的差都在10-5級別。把本文的方法應用到定位算法中，同樣應用上述4個時刻的軌道數據，計算了國際空間站的星下點的定位結果，跟同樣輸入的商業軟件STK定位結果進行了比較，4個時刻定位結果的差異都在0.5m以內。通過以上比較可知，本文提出的方法可跟傳統方法獲得相同的效果，證明本文方法的正確性，本方法將這兩次坐標系轉換縮減為一個，從而避免了應用地球的章動、極移和歲差等信息，為直接定位算法提供了一種新的坐標系轉換方法，也擴展了四元數方法應用領域。特別適合于大型低軌載人平臺以及低軌衛星遙感影像的應用，因為這類航天器在全球定位系統的幫助下，可提供定義在地心固定坐標系的位置和速度信息，該方法具有一定的應用前景。

References)

[1]呂爭, 傅俏燕, 王小燕. “資源三號”衛星正視影像區域網平差[J]. 航天返回與遙感, 2014, 35(2): 72-80. LV Zheng, FU Qiaoyan, WANG Xiaoyan. Research on Block Adjustment of ZY-3 Satellite NAD Images[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(2): 72-80. (in Chinese)

[2]王任享. 中國無地面控制點攝影測量衛星追述(二)-1∶1 萬傳輸型攝影測量衛星技術思考[J]. 航天返回與遙感, 2014, 35(2): 1-5. WANG Renxiang. Chinese Photogrammetry Satellite without Ground Control Points(2)-Technical Thinking of 1∶10 000Scale Data-transferring Photogrammetry Satellite[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(2): 1-5. (in Chinese)

[3]WOLFE R E, NISHIHAMA M, FLEIG A J, et al. Achieving Sub-pixel Geolocation Accuracy in Support of MODIS Land Science[J]. Remote Sensing of Environment, 2002, 83: 31-49.

[4]DI Kaichang, MA Ruijin, LI Rongxing. Rational Functions and Potential for Rigorous Sensor Model Recovery[J]. Photogrammetric Engineering & Remote Sensing, 2003, 69(1): 33-41.

[5]POLI D, TOUTIN T. Review of Developments in Geometric Modelling for High Resolution Satellite Pushbroom Sensors[J]. The Photogrammetric Record, 2012, 27(137): 58-73.

[6]張過, 厲芳婷, 江萬壽, 等. 推掃式光學衛星影像系統幾何校正產品的 3維幾何模型及定向算法研究[J]. 測繪學報, 2010, 39(1): 34-38. ZHANG Guo, LI Fangting, JIANG Wanshou, et al. Study of Three-dimensional Geometric Model and Orientation Algorithms for Systemic Geometric Correct ion Product of Push-broom Optical Satellite Image [J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 34-38. (in Chinese)

[7]TONG X, LIU Shijie, WENG Qihao. Bias-corrected Rational Polynomial Coefficients for High Accuracy Geo-positioning of QuickBird Stereo Imagery[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(2): 218-226.

[8]張繼賢, 鄧喀中, 程春泉, 等. 月球遙感影像高精度定位研究[J]. 遙感學報, 2010, 14(3): 423-436. ZHANG Jixian, DENG Kazhong, CHENG Chunquan, et al. Study on High-accuracy Orientation with Lunar Remote Sensing Imagery [J]. Journal of Remote Sensing, 2010, 14(3): 423-436. (in Chinese)

[9]閆利, 聶倩, 趙展. 利用四元數描述線陣CCD 影像的空間后方交會[J]. 武漢大學學報·信息科學版, 2010, 35(2): 201-204. YAN Li, NIE Qian, ZHAO Zhan. Space Resection of Line Scanner CCD Image Based on the Description of Quaternions [J]. Geomatics and Information Science of Wuhan University, 2010, 35(2): 201-204. (in Chinese)

[10]江剛武, 姜挺, 王勇, 等. 基于單位四元數的無初值依賴空間后方交會[J]. 測繪學報, 2007, 36(2): 169-175. JIANG Gangwu, JIANG Ting, WANG Yong, et al. Space Resection Independent of Initial Value Based on Unit Quaternions[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 169-175. (in Chinese)

[11]盛慶紅, 姬亭, 劉微微, 等. 對偶四元數線陣遙感影像幾何定位[J]. 中國圖象圖形學報. 2012, 17(10): 1319-1326. SHENG Qinghong, JI Ting, LIU Weiwei, et al. Geo-positioning Line-array CCD Images with Dual Quaternion[J]. Journal of Image and Graphics, 2012, 17(10): 1319-1326. (in Chinese)

[12]SHENG Qinghong, SHAO Sa, XIAO Hui, et al. Relative Orientation Dependent on Dual Quaternions[J]. The Photogrammetric Record, 2015, 30(151): 300-317.

[13]張春森, 張覓. 依初值與無初值單位四元數空間后方交會的比較[J]. 測繪科學, 2015, 40(4): 3-10. ZHANG Chunsen, ZHANG Mi. Comparison of Space Resection based on Unit Quaternion between Initial-value based and Non-initial-value based Methods[J]. Science of Surveying and Mapping, 2015, 40(4): 3-10. (in Chinese)

[14]程春泉, 鄧喀中, 張繼賢, 等. 基于ECR與ECI星歷數據的遙感影像定位[J]. 測繪科學, 2010, 35(2): 13-15. CHENG Chunquan, DENG Kazhang, ZHANG Jixian, et al. Positioning of Remote Sensing Image based on Ephemeris in ECR or ECI[J]. Science of Surveying and Mapping, 2010, 35(2): 13-15. (in Chinese)

[15]堃胡 , 陳剛, 孫韜, 等. 一種大傾角敏捷成像衛星影像的直接定位方法[J]. 測繪科學, 2015, 40(2): 59-65. HU Kun, CHEN Gang, SUN Tao, et al. A Direct Positioning Method of Agile Satellite with Large-tilt-angle Imaging[J]. Science of Surveying and Mapping, 2015, 40(2): 59-65. (in Chinese)

[16]WOLFE R E. MODIS Level 1A Earth Location: Algorithms Theoretical Basis Document[EB/OL]. (1997). [2016]URL: http://modis.gsfc.nasa.gov/data/atbd/atbd_mod28_v3.pdf.

[17]NGA.STND.0036_1.0.0_WGS84. National Geospatial-intelligence Agency (NGA) Standardization Document, Department of Defense World Geodetic System, Its Definition and Relationships with Local Geodetic System. 2_13-2_15 [EB/OL]. (2014). [2016]http://earth-info.nga.mil/GandG/publications/NGA_STND_0036_1_0_0_WGS84/NGA. STND.0036_1.0.0_WGS84.pdf.

[18]HART J C, FRANCIS G K, KAUFFMAN L H. Visualizing Quaternion Rotation[J]. ACM Transactions on Graphics, 1994, 13(3): 256-276.

[19]HANSON A J. Visualizing Quaternions[M]. San Francisco: Morgan Kaufmann, 2000: 54-56.

Direct Transformation from Orbital to Earth-centered Earth-fixed Reference Frame

DOU Changyong1,2,3YUE Xijuan3

（1 Institute of Electronics，Chinese Academy of Sciences，Beijing 100190，China）
（2 University of Chinese Academy of Sciences，Beijing 100049，China）
（3 Institute of Remote Sensing and Digital Earth，Chinese Academy of Sciences，Beijing 100094，China）

Coordinate transformation is key steps of the precise geolocation of the satellite remote sensing imagery using navigation dataset. By utilizing the sensor’s position and velocity defined in the earth-centered and earth-fixed (ECEF) reference frame, the transformation from orbital reference frame to ECEF can be performed directly by using quaternion. In traditional direct geolocation algorithm of remote sensing imagery, this transformation usually includes two steps: transformation from orbital to earth centered initial (ECI), and from ECI to ECEF reference frame. The proposed method in this paper reduces the two transformations into one, namely, transforming from orbital to ECEF directly, thus avoiding using the earth’s nutation, precession, and polar motion which are difficult to obtain for the transformation from ECI to ECEF reference frame. Comparing with the transformed results using the traditional method, and geolocation results simulated using commercial satellite tool kit (STK) software suggested that the proposed method is correct. The proposed method is suited for positioning remote sensing image obtained on earth observing platform in low earth orbit, for the LEO vehicle’s position and velocity information defined in the ECEF reference frame is provided.

TP391.9

: A

: 1009-8518(2016)05-0086-09

10.3969/j.issn.1009-8518.2016.05.010

竇長勇，男，1979年生，博士。研究方向為攝影測量與遙感及大型載人對地觀測平臺遙感應用。E-mail: doucy@radi.ac.cn。

（編輯：王麗霞）

2016-03-24

國家自然科學基金（41201481）