基于PRP共軛梯度的重構算法研究
劉 艷,李 雷
(南京郵電大學 非結構化數據計算理論與應用研究中心,江蘇 南京 210046)
基于PRP共軛梯度的重構算法研究
劉 艷,李 雷
(南京郵電大學 非結構化數據計算理論與應用研究中心,江蘇 南京 210046)
SL0算法是一種基于近似l0范數的壓縮感知信號重建算法。通過尋找一個光滑函數近似l0范數,從而將l0范數最小化問題轉化為光滑函數的最優化問題,采用最速下降法和梯度投影原理逐步逼近最優解。針對求解函數的最優化問題,NSL0算法提出用修正牛頓法對雙曲正切函數進行求解,但此算法需求解函數的HESS矩陣,計算量較大,影響重構速度。文中提出一種重構速度更快的基于光滑l0范數和PRP共軛梯度法的重構算法—PRPSL0。用雙曲正切函數近似l0范數得到一個新的最優化問題,采用PRP共軛梯度法以及梯度投影原理推導出下降方向并逐步逼近問題的最優解。實驗結果表明,在相同的測試條件下,該算法在收斂速度及重建效果方面均優于其他算法。
壓縮感知;重構算法;光滑函數;共軛梯度法
1 概 述
壓縮感知[1-5](Compressive Sensing,CS),又稱壓縮采樣,是近幾年出現的一種新型壓縮采樣方法。該理論是指對可壓縮的信號通過遠低于Nyquist標準的方式進行數據測量,同時仍能精確恢復出原始信號。
根據壓縮感知[3-5]理論,只要信號是可壓縮的或在某個變換域上是稀疏的,那么就可以用一個與變換基不相關的觀測矩陣將高維信號投影到一個低維空間上,然后通過求解一個優化問題就可以從這些少量的投影中以高概率重構原信號。
在壓縮感知處理過程中,主要分為三個階段:
(1)具有稀疏表示能力的過完備字典設計;
(2)滿足非相干性或等距約束性準則的測量矩陣設計;
(3)快速魯棒的信號重構算法設計。
重構算法的設計是壓縮感知理論中關鍵的一部分,它對于壓縮后信號的精確重構以及采樣過程中的準確性驗證均有著重要的意義。Candès等證明了信號重構問題可以通過求解l0范數最小化問題加以解決。文中將討論壓縮感知圖像重構中的l0范數最小化問題。
壓縮感知理論的基本原則和目標就是從較少的相對不完整的測量值b=Ax中恢復出k稀疏(對于長度為N的向量(實際上是指一個N維離散信號)來說,它的N個元素值只有k個是非零的,其中k?N)的信號x∈Rn。理論上,恢復信號x最簡單的方法是求解模型(1)的最小化問題。
(1)
其中,‖x‖0為x中非零元素的個數;b為測量向量;A為m×n維的測量矩陣且m 文中提出一種基于l0范數和PRP共軛梯度法的重構算法,尋找一個能夠近似l0范數的光滑函數,將模型(1)轉化為一個最優化問題,結合PRP共軛梯度法求解函數的最優解。 l0范數定義為x=[x1,x2,…,xN]T中非零元素的個數,換句話說 (2) (3) 由此可知x=[x1,x2,…,xN]T的l0范數是由不連續函數f(x)決定的,如果能夠尋找一個光滑連續的函數來替代f(x),那么l0范數的最小化問題也可以間接求出。為了保證近似的效果,將引入一個含有參數σ的連續函數來解決l0范數的最小化問題。 定理1:若函數族fσ能夠近似滿足KroneckerDelta公式: (4) 或者 (5) 那么求解l0范數問題可以轉化為求解該函數族fσ和的問題。 (6) 那么對于一個函數族fσ(xi),式(6)可以進一步轉化為: (7) 則求解x的l0范數就是求解 (8) 若函數族fσ滿足式(5),那么式(2)可以轉化為: (9) 求解式(3)即是求解 (10) 得證。 能夠滿足該性質的函數有很多,SL0[9]算法則選取了光滑連續的高斯函數族(見式(11))來近似l0范數[10-12],將l0范數最小化問題轉化為一個連續函數的極小化問題。 (11) (12) SL0算法使用最速下降法和梯度投影原理來求解l0范數最優解,但是最速下降的探索路徑出現了“鋸齒”形狀,具有不能求出全局最優解的缺點,同時其搜索路徑難以估計。因此,最速下降法具有慢收斂性的缺點。文獻[13]提出了復合三角函數(見式(13))來近似l0范數。 (13) 由于牛頓法具有收斂速度快的優點,因此文獻[13]用牛頓法尋求最優解。 相比較于最速下降法和牛頓法,共扼梯度法既克服了最速下降法的慢收斂性,又避免了Newton法計算量大和局部收斂性的缺點。因此,文中提出使用共扼梯度法來求解模型(1)的最優解。 3.1 函數的選擇 SL0算法的第一步是選擇一個連續光滑的函數來近似l0范數,文中將選擇文獻[13]中提到的雙曲正切函數來近似l0范數。 (14) 其中,σ為參數;xi為是X的第i個分量。 由式(9)可以推出 (15) 定義: (16) 由l0范數的定義可知,模型(1)中‖x‖0表示x中非零元素的個數,因此,l0范數可以近似地表示為: (17) 綜上,模型(1)可以表示為: (18) 當σ=0時,‖x‖0=Gσ(X),所以式(13)的解就是模型(1)的解,當σ最小且Gσ(X)最小時可以求出使l0范數最小化的量,但實際應用中σ無法取到0,因此選擇一個遞減序列σ1,σ2…,對每一個σi對應的目標函數求最優解,直到σ足夠小為止。 3.2 基于共扼梯度法的重構算法 求解式(18)的方法有很多,各種求解的方法都有其優缺點。最速下降法主要存在兩個問題:探索路徑存在“鋸齒現象”,影響收斂速度;搜索步長難以估計。牛頓法則很好地彌補了最速下降法的缺點,在文獻[13]中提到用阻尼牛頓法來確定步長,很大程度上提高了收斂速度,但是牛頓法需要在求解Hess矩陣的同時保證矩陣是正定的,因此計算的復雜度較大。 針對以上問題,文中提出的共扼梯度法既克服了最速下降法的慢收斂性,又避免了Newton法計算量大和局部收斂性的缺點[14]。共軛梯度法的基本思想是把共軛性與最速下降法相結合,利用已知點處的梯度構造一組共軛方向,并沿這組方向進行搜索,求出目標函數的極小點。根據共軛方向基本性質,該方法具有二次終止性。共軛梯度法中可行的下降方向是d(k)=-G(xk)+βkd(k-1)。其中,βk可由Fletcher-Reeveshe[15]和Polak-Ribiere-Polyak公式得到。當算法產生一個較小誤差時,PRP公式得到的下一個搜索方向會自動靠近目標函數的負梯度方向,從而保證方向的下降性,且實踐證明Polak-Ribiere-Polyak算法優于FR算法,因此文中將使用Polak-Ribiere-Polyak公式得到的βk計算搜索方向。 因此PRP共軛梯度SL0算法的具體步驟如下: 迭代過程: forj=1,2,…,J 1)σ=σj fork=1,2,…,L (1)可行的下降方向: d(k)=-G(xk)+βkd(k-1) 其中,β由Polak-Ribiere-Polyak公式得到。 (2)梯度投影法求解可行方向: d(k)=(I-AT(AAT)-1A)d(k) (3)由精確一維搜索確定步長μ:令xk=xk-1+μd(k) 為了說明文中提出的算法的優越性,將使用Matlab進行測試。文獻[10]將NSL0與GP、GPSR、OMP等算法進行比較,并驗證NSL0比其他算法重構性能好。因此,文中將比較SL0、NSL0、CGSL0以及PRPSL0四種算法的性能。圖1給出了壓縮比為0.5時四種算法的重構效果圖。 圖1 算法重建效果對比圖 表1為在壓縮比M/N=0.5時,SL0,NSL0,CGSL0以及PRPSL0在均方誤差、峰值信噪比和重構時間方面的對比結果。 表1 同一壓縮比下各算法重建性能對比 由表1可以看出,SL0,NSL0和CGSL0的均方誤差都大于PRPSL0,PRPSL0的峰值信噪比相對于其他算法沒有提高太多,但重構時間比SL0少了1.5s。由此可以看出,PRPSL0的重構性能高于其他三種算法,重構效果相對較好。 表2為在壓縮比為0.1~0.6時四種算法重構時間的對比結果。 表2 不同壓縮比下各算法的重構時間 s 從表中可明顯看出,當壓縮比相同時,PRPSL0算法所需的重構時間遠遠少于其余三種算法。同時,隨著壓縮比的增大,四種算法所需的重構時間均有所減少,但相比于其他三種算法,PRPSL0算法的重構時間最少。由此可以看出PRPSL0算法在重構速度方面的優勢。 圖2為不同壓縮比下四種算法在收斂速度、均方誤差和峰值信噪比方面的性能比較。 圖2 不同壓縮比下各算法的性能比較 從圖中可以看出,文中提出的重構算法的均方誤差以及峰值信噪比在壓縮比為0.3~0.8之間時,明顯高于其他三種算法,在不同采樣率下,PRPSL0重構時間遠遠少于其他三種算法。因此,在不同的采樣率下,PRP共軛梯度法重構圖像所需要的時間較少,收斂速度較快,重構效果好,體現了一定程度的優勢。 在對SL0和NSL0兩種算法進行研究的基礎上,分析比較最速下降法和修正牛頓法[16]的優缺點。由于最速下降法收斂性較慢,并且探索路徑存在“鋸齒現象”,從而影響收斂速度和難以估計探索步長,而牛頓法需要求解Hess矩陣的同時保證矩陣是正定的,計算量大。針對這兩種算法存在的一些不足,文中提出了基于共軛梯度法的l0范數重構算法。由于PRPSL0算法只需求解一階導數,因此節省了很多時間,既能克服最速下降法的慢收斂性,又避免了Newton法計算量大和局部收斂性的缺點。實驗結果表明,該算法在收斂速度與重構誤差方面均有很大提高。今后將致力于在重構精度方面進一步優化算法,使其能夠真正應用到圖像及視頻重構中去。 [1]CandèsE.Compressivesampling[C]//Proceedingsoftheinternationalcongressmathematicians.Madrid,Spain:[s.n.],2006:1433-1452. [2]CandèsE,RombergJ.Quantitativerobustuncertaintyprinciplesandoptimallysparsedecompositions[J].FoundationsofComputerMath,2006,6(2):227-254. [3]DonohoDL.Compressedsensing[J].IEEETransactionsonInformationTheory,2006,52(4):1289-1306. [4]CandèsEJ,RombergJ,TaoT.Robustuncertaintyprinciples:exactsignalreconstructionfromhighlyincompletefrequencyinformation[J].IEEETransactionsonInformationTheory,2006,52(2):489-509. [5] 石光明,劉丹華,高大化,等.壓縮感知理論及其研究進展[J].電子學報,2009,37(5):1070-1081. [6]PantJK,LuWusheng,AntoniouA.Reconstructionofsparsesignalbyminimizingareweightedapproximatel0-norminthenullspaceofthemeasurementmatrix[J].IEEETransactionsonSignalProcssing,2005,53(8):3010-3022. [7]TroppJ,GillbertA.Signalrecoveryfromrandommeasurementsviaorthogonalmatchingpursuit[J].IEEETransactionsonInformationTheory,2007,53(12):4655-4666. [8]ChartrandR,YinW.Interativereweightednormalgorithmforcompressivesensing[C]//ProcofIEEEinternationalconferenceonacoustics.[s.l.]:IEEE,2009:3869-3873. [9]MohimaniH,Babaie-ZadehM,JuttenC.Afastapproachforovercompletesparsedecompositionbasedonsmoothedl0norm[J].IEEETransactionsonSignalProcessing,2009,57(1):289-301. [10] 趙瑞珍,林婉娟,李 浩,等.基于光滑l0范數和修正牛頓法的壓縮感知重建算法[J].計算機輔助設計與圖形學學報,2012,24(4):478-484. [11] 林婉娟,趙瑞珍,李 浩.用于壓縮感知信號重建的NSL0算法[J].新型工業化,2011,1(7):78-84. [12] 楊良龍,趙生妹,鄭寶玉,等.基于SL0壓縮感知信號重建的改進算法[J].信號處理,2012,28(6):834-841. [13] 齊煥芳,徐源浩.用于壓縮感知信號重建的SL0改進算法[J].電子科技,2015,28(4):27-30. [14] 解可新,韓 健,林友聯.最優化方法[M].天津:天津大學出版社,2004. [15] 陸 望.基于壓縮感知的信號重構算法研究及應用[D].南京:南京郵電大學,2015. [16]SunWenyu,YuanYaxiang.Optimizationtheoryandmethods[M].NewYork:Springer,2006. Research on Reconstruction Algorithm Based on PRP Conjugate Gradient LIU Yan,LI Lei (Research Center of Unstructured Data Calculation Theory and Application,Nanjing University of Posts and Telecommunications,Nanjing 210046,China) The SL0algorithmisareconstructiononeincompressivesensingbasedonapproximatel0norm.Byusingasmoothfunctiontoapproximatethel0normandturnthel0normproblemintotheoptimizationproblem,itapproachesthesolutionusingthespecificiterationprocesswiththesteepestdescentmethodandgradientprinciple.Forsolvingtheoptimizationproblem,theNSL0algorithmusestherevisedNewtonmethodtosolvethehyperbolictangentsequence,butitdemandstheHESSmatrixofthefunction,sothelargeamountofcalculationinfluencesthespeedofreconstruction.Areconstructionalgorithmisputforwardbasedonthesmoothedl0normandconjugategradientmethodcalledPRPSL0.Thehyperbolictangentsequenceisutilizedtoapproximatethel0norm,thenapplyingPRPconjugategradientmethodandgradientprincipletosolvethedropdirectionandtheoptimalsolution.Theexperimentalresultsshowthattheproposedalgorithmissuperiortootheralgorithmsbothintermsofconvergencespeedandreconstructioneffect. compressive sensing;reconstruction algorithm;smooth function;conjugate gradient method 2015-12-02 2016-03-09 時間:2016-08-01 國家自然科學基金資助項目(61070234,61071167,61373137,61501251);南京郵電大學引進人才科研啟動基金資助項目(214191);江蘇省普通高校研究生科研創新計劃資助項目(KYZZ15_0236) 劉 艷(1991-),女,碩士,研究方向為非線性分析及其應用;李 雷,教授,研究方向為智能信號處理和非線性科學及其在通信中的應用。 http://www.cnki.net/kcms/detail/61.1450.TP.20160801.0907.042.html TP A 1673-629X(2016)08-0055-05 10.3969/j.issn.1673-629X.2016.08.012
2 SL0算法基礎
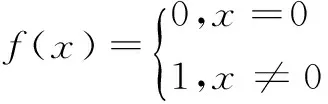



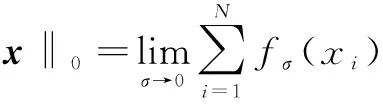


3 基于SL0的一種改進算法



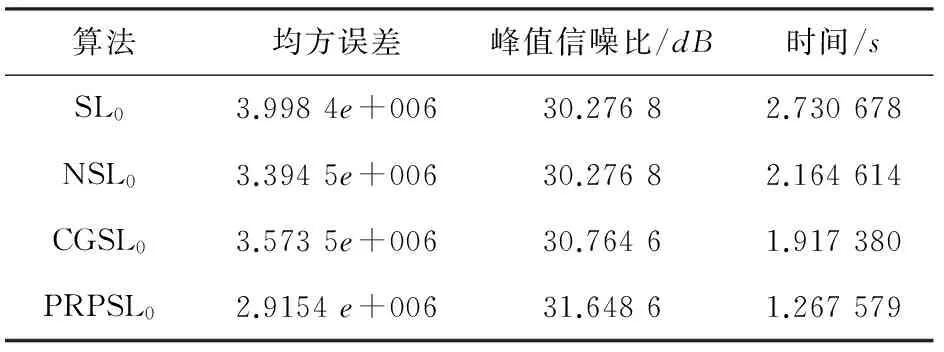
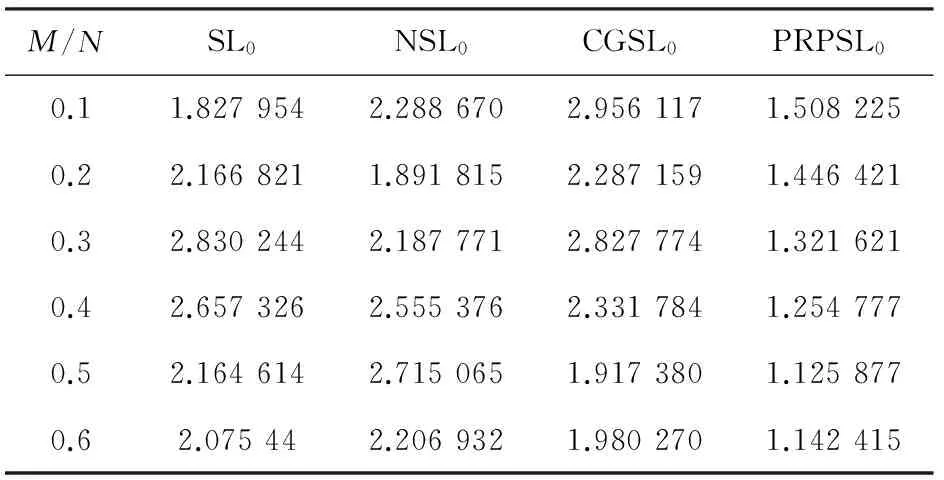
4 實驗結果及分析


5 結束語

