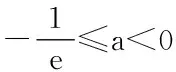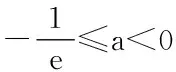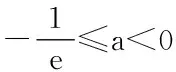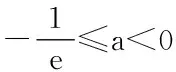一題多變賞析函數中的任意性與存在性問題

?王躍

(作者單位：安徽省宿州市靈璧縣中學 234200)

一題多變賞析函數中的任意性與存在性問題

?王躍

函數中的任意性與存在性問題,也即函數中的恒成立與能成立問題,已成為高中數學考查的重點和難點,也是高考的熱點題型。這類問題主要涉及到函數的最值和值域,常與導數相結合,并且與數形結合、分類討論、轉化與化歸等數學思想緊密聯系,綜合性較強，也是一類易混淆、易出錯的問題。因此,對此問題,筆者通過一題多變來研究函數中的任意性與存在性問題，并給出解決相關問題的方法歸納,供同仁在教學中參考,同時希望對復習備考的學生有所啟示和幫助。

例:已知函數f(x)=x2-2x+2，g(x)=ax+lnx(a∈R),若存在x1∈[0,1]，x2∈[1,e]使得f(x1)

(1) 當a≥0時,由于g′(x)>0,所以

g(x)=ax+lnx在x∈[1,e]單調遞增,故

[g(e)]max=ae+1。

根據[f(x)]min<[g(x)]max即10;

x∈[1,e]單調遞增,[g(e)]max=ae+1<1與[f(x)]min<[g(x)]max矛盾。故a不存在;

(4) 當a≤-1時,g(x)=ax+lnx在

x∈[1,e]單調遞減,所以[g(1)]max=a，根據[f(x)]min<[g(x)]max,所以a>1，又因為a≤-1,故a不存在;

綜上所述:實數a的取值范圍為(0,+∞)。

歸納:x1∈D,x2∈E,f(x1)

?[f(x)]min<[g(x)]max。

變式1：若對?x1∈[0,1],?x2∈[1,e]使f(x1)

解析：?x1∈[0,1],?x2∈[1,e]使f(x1)

與[f(x)]max<[g(x)]max矛盾,不符合題意，故a不存在;

(4)當a≤-1時，g(x)=ax+lnx在x∈[1,e]單調遞減，所以 [g(1)]max=a，根據[f(x)]max<[g(x)]max，所以a>2，又因為a≤-1，故a不存在;

歸納:?x1∈D?x2∈E,f(x1)

?[f(x)]max<[g(x)]max。

變式2：若對?x1∈[0,1]，?x2∈[1,e]使f(x1)=g(x2)成立，求實數a的取值范圍(其中e為自然對數的底數)

解：設f(x)的值域為集合A，g(x)的值域為集合B，對?x1∈[0,1]，?x2∈[1,e]使f(x1)=g(x2)?A?B。易知A=[1,2]。

(1) 當a≥0時，因為g(x)在x∈[1,e]單

歸納：?x1∈D,?x2∈E,f(x1)=g(x2)

?f(x)的值域?g(x)的值域。

變式3：若?x1∈[0,1]，?x2∈[1,e]使f(x1)=g(x2)成立，求實數a的取值范圍(其中e為自然對數的底數)。

解：設f(x)的值域為集合A,g(x)的值域為集合B,對存在x1∈[0,1]，x2∈[1,e]使f(x1)=g(x2)?A∩B≠φ，易知A=[1,2]。

(4)當a≤-1時,g(x)=ax+lnx在x∈[1,e]單調遞減,B=[a,ae+1],因為ae≤-e,所以ae+1≤1-e<0，故a不存在;

歸納:?x1∈D,?x2∈E,f(x1)=g(x2)

?f(x)的值域∩g(x)的值域≠φ。

變式4：若對?x1∈[0,1]，?x2∈[1,e]使f(x1)

解析:若對?x1∈D,?x2∈E使f(x1)

(1)當a≥0時,[g(x)]min=a,所以a>2;

(5)當a≤-1時,g(e)=ae+1<2,不符合題意;

綜上所述:實數a的取值范圍是(2,+∞)。

歸納:?x1∈D,?x2∈E,f(x1)

?[f(x)]max<[g(x)]min。

通過對上述例題進行一題多變可以看出,此類型題目中均含有兩個函數,并且含有兩個變量。由于這兩個變量在各自區間上的取值具有任意性,因此,這類問題最終轉化為函數值域或最值問題加以解決。

(作者單位：安徽省宿州市靈璧縣中學 234200)