基于高斯偽譜法的化-電混合推進系統(tǒng)轉移軌道優(yōu)化設計

楊博,陳子勻,溫正,苗峻

1.北京航空航天大學宇航學院,北京100091 2.中國空間技術研究院通信衛(wèi)星事業(yè)部,北京100094

基于高斯偽譜法的化-電混合推進系統(tǒng)轉移軌道優(yōu)化設計

楊博1,*,陳子勻1,溫正2,苗峻1

1.北京航空航天大學宇航學院,北京100091 2.中國空間技術研究院通信衛(wèi)星事業(yè)部,北京100094

提出利用化-電混合模式推進系統(tǒng)完成地球同步衛(wèi)星軌道轉移任務,該推進系統(tǒng)極具應用前景,能夠滿足高有效載荷率、高入軌精度的工程實踐需求。并針對基于該混合模式推進系統(tǒng)的轉移軌道的優(yōu)化方法展開研究,提出一種多階段最優(yōu)控制問題(OCP)的高斯偽譜法求解方法。該方法通過分段點的關聯(lián)設置,將多個經高斯偽譜法轉化而來的非線性規(guī)劃問題轉化為一個連貫的非線性規(guī)劃問題(NLP)。兩個不同算例的仿真過程與分析結果表明,該方法能夠有效地解決多階段非光滑連接軌道的優(yōu)化問題,具有運算效率高、收斂性半徑大、求解精度高等優(yōu)點,可便捷地處理化-電混合模式推進系統(tǒng)的轉移軌道優(yōu)化設計問題。

電推進;混合模式;多階段;同步軌道;高斯偽譜法

電推進相對于化學推進具有高比沖的突出優(yōu)勢,可大幅降低衛(wèi)星推進劑攜帶量,從而提高衛(wèi)星有效載荷比,延長在軌壽命和降低發(fā)射質量[1]。但近地空間環(huán)境特性、空間任務時間約束以及航天器功率約束嚴重制約電推進系統(tǒng)在同步軌道轉移任務中的推廣應用[2]。在該背景下,采用化-電混合模式推進系統(tǒng)完成地球同步軌道轉移任務是一種極具應用前景的軌道轉移方式。航天器與運載火箭分離后,采用化學發(fā)動機迅速將同步衛(wèi)星送入較高軌道,完成大部分的傾角改變與軌道提升,既避免了近地環(huán)境對衛(wèi)星產生的影響,又節(jié)省了軌道轉移時間;之后,采用電推進方式完成同步衛(wèi)星最后的軌道轉移以及最終定軌,既節(jié)省了推進劑消耗質量,又提高了軌道位置精度。

簡單的功能組合并不能得出最優(yōu)的任務方案,還須對混合模式推進系統(tǒng)的轉移軌道進行設計與優(yōu)化[3]。受制于空間技術的發(fā)展水平以及對空間電推進系統(tǒng)的應用定位,鮮有研究者針對基于混合模式推進系統(tǒng)的軌道轉移任務開展研究[4],大部分的空間任務分析、軌道設計與優(yōu)化以及各種數(shù)值優(yōu)化算法等均集中在小推力連續(xù)軌道轉移問題上。

優(yōu)化問題的求解主要分為兩類:間接法和直接法[5]。此外還有智能優(yōu)化算法[6](如遺傳算法和粒子群算法),但一般難以保證搜索到的解是最優(yōu)解。間接法利用極小值原理得到最優(yōu)控制的必要條件,具有求解精度高的特點,但對于較復雜非線性系統(tǒng)則面臨求解過程繁復、收斂速度慢的突出困難。直接法[7-9]將最優(yōu)控制問題(OCP)在所選取的節(jié)點處離散,節(jié)點處的狀態(tài)和控制量作為未知量,性能指標和狀態(tài)方程表示為離散點值的函數(shù),轉化為非線性規(guī)劃問題(NLP),利用NLP算法進行求解,節(jié)點間的值則通過插值法求得。直接法一般采用的插值方法為線性和三次樣條,而利用全局正交多項式進行插值的方法稱為偽譜法。其中高斯偽譜法由于其計算量小、收斂半徑大、精度高等優(yōu)點,得到了廣泛的應用。與其他求解OCP的數(shù)值方法相比,高斯偽譜法有很多的優(yōu)勢,首先也是最重要的一點就是滿足協(xié)調映射定理,即轉化后得到的非線性規(guī)劃問題的KKT條件精確等價于離散一階必要條件,因此高斯偽譜法轉化得到的NLP以譜精度收斂于OCP的最優(yōu)解。

基于混合模式推進系統(tǒng)的地球同步轉移軌道是多階段非光滑的,若使用間接法對該多階段最優(yōu)控制問題進行求解,則須對各個分段點進行繁復猜測。此外,電推力器的小推力特性[7]使得任務時間大大增加,數(shù)據(jù)處理量隨之增大,求解過程很難收斂。本文結合高斯偽譜法在連續(xù)軌道優(yōu)化中的應用[10-11],提出了一種多階段轉移軌道的高斯偽譜法求解方法,可以很好地解決所遇到的難題。

1 問題建模

同步軌道衛(wèi)星在利用混合模式推進系統(tǒng)進行軌道轉移時,根據(jù)推力特性可初步將整個過程分為兩段,即化推段與電推段。其中化推段可根據(jù)化學發(fā)動機點火次數(shù)的不同分為多個化推開機段與化推自由段;電推段則為連續(xù)推進過程。若化學發(fā)動機進行兩次點火變軌,則進一步細分,整個軌道被分為4段,按時間順序依次為化推開機段、化推自由段、化推開機段、電推段。可以看出,發(fā)動機的點火次數(shù)直接影響問題求解的復雜程度。結合混合模式推進系統(tǒng)下地球同步軌道衛(wèi)星的軌道轉移任務的實際需求,進行確定任務時限下的燃料優(yōu)化問題的數(shù)學描述[12-13]。

1.1 動力學描述

化學發(fā)動機與電推力器的推力特性差別很大,要建立全局優(yōu)化模型必須尋找一種兩者通用的動力學模型,以保證無論是在低比沖大推力情況下還是在高比沖小推力的情況下,數(shù)據(jù)處理過程均能高精度地穩(wěn)定進行。由于軌道轉移任務耗時較長,尤其是電推進階段,推力小,耗時長,采用不同的軌道動力學模型會對軌道機動的優(yōu)化進程產生影響,因此建立適當?shù)能壍绖恿W模型是混合模式推進系統(tǒng)應用策略設計與優(yōu)化的基礎。改進春分點軌道要素動力學模型,當偏心率和軌道傾角為零時,用經典軌道要素描述的軌道動力學方程存在奇點,因此這里引入一種消除奇異的改進春分點軌道要素[14-15]。這組軌道要素只有在軌道傾角為180°時才會產生奇異,而這種情況在有限推力軌道轉移問題中幾乎不存在,因此應用面較廣。定義如下:

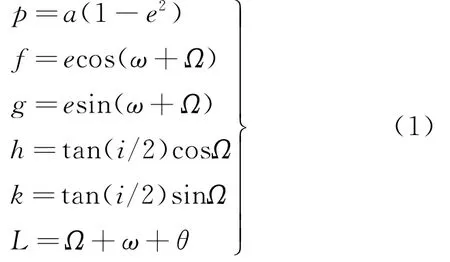
相應的動力學方程為

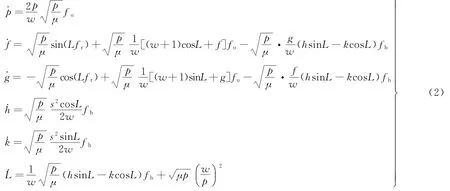
式中:μ為引力常數(shù);w=1+fcosL+gsinL;s2=1+h2+k2;fu、fr、fh分別為推力的橫向、徑向、法向分量。

1.2 最優(yōu)控制問題描述

Bolza型最優(yōu)控制問題一般描述為:求解最優(yōu)控制律u(t)∈RNu,使得系統(tǒng)從一個狀態(tài)轉移至另一狀態(tài)過程中的性能函數(shù)最小,其數(shù)學描述為

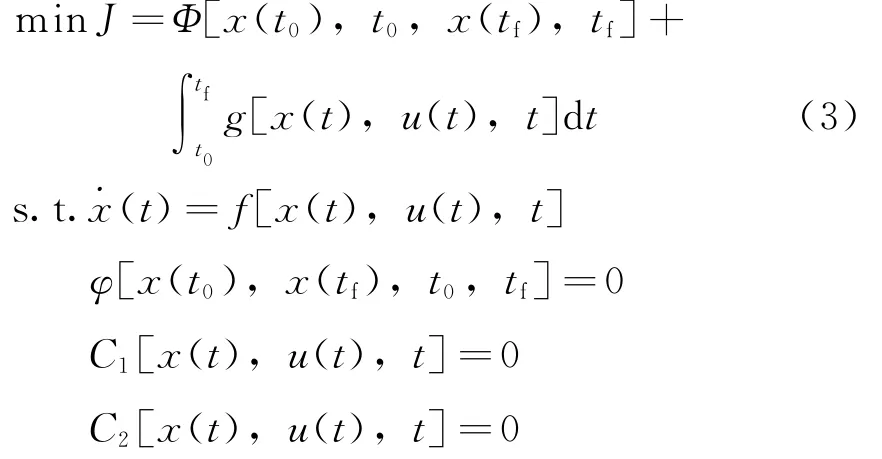
式中:J∈R為性能指標;Φ(·)∈R為Mayer型指標;g(·)∈R為Lagrange型性能指標;t∈R為時間變量;t0為初始時間;tf為終止時間;x∈RNx為狀態(tài)向量;u∈RNu為控制向量;φ為初始和終端約束函數(shù)向量;C1、C2分別為等式與不等式路徑約束向量。

以上為連續(xù)光滑最優(yōu)控制問題的描述,當最優(yōu)控制問題為多階段的非光滑過程時,描述方式與解決方法均有不同。基于混合模式推進系統(tǒng)的衛(wèi)星同步轉移軌道的優(yōu)化問題為多階段最優(yōu)控制問題。可描述如下:

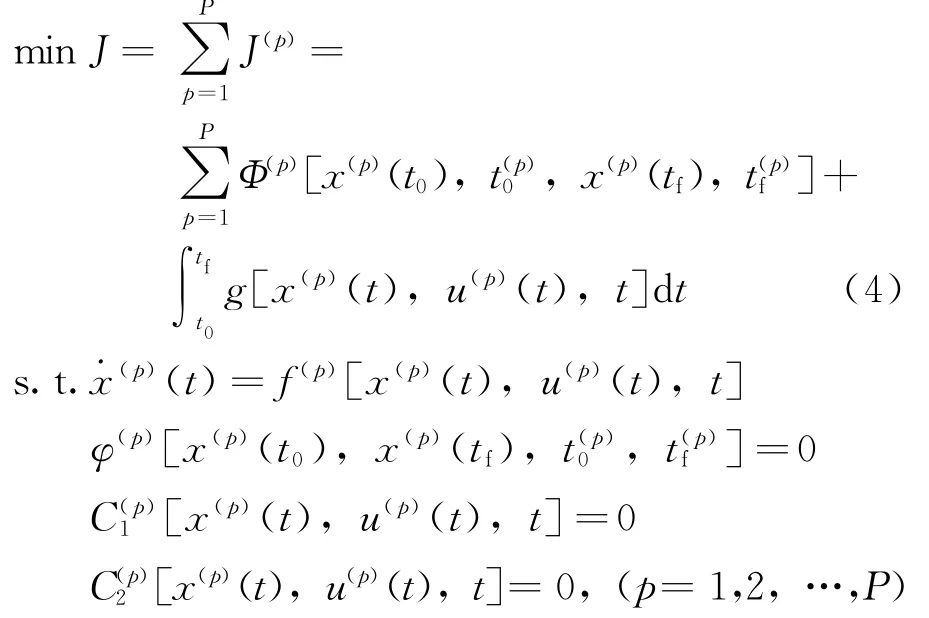
為保證求解的分段點的連續(xù)性,須進行段間連續(xù)性約束:

P(s)[x(psl)(tf),t(psl)f,x(psu)(t0),t(psu)0]=0, (pl,pu∈[1,2,…,P],s=1,2,…,L)(5)

以上為段間聯(lián)接約束,軌道總共分為P段,p∈[1,2,…,P]為分段序號,L為待聯(lián)接的段數(shù),psl∈[1,2,…,P],(s=1,2,…,L)為左側階段序號,psu∈[1,2,…,P],(s=1,2,…,L)為右側階段序號。

2 高斯偽譜法求解

高斯偽譜法求解最優(yōu)控制問題的主要思路是通過在一系列Legendre-Gauss(LG)點上構造Lagrange插值多項式來近似系統(tǒng)的狀態(tài)變量和控制變量,然后將連續(xù)最優(yōu)控制問題轉換為非線性規(guī)劃問題,再利用發(fā)展較成熟的解決非線性規(guī)劃問題方法進行求解,最終得到原最優(yōu)控制問題的解。

本文從連續(xù)光滑最優(yōu)控制問題的高斯偽譜法求解思路出發(fā),逐步推導出適用于多階段轉移軌道優(yōu)化的高斯偽譜法求解策略。

2.1 高斯偽譜法求解步驟

(1)區(qū)間變換

設最優(yōu)控制問題的時間區(qū)間為[t0,tf],采用高斯偽譜法則需將時間區(qū)間歸一化,轉換到[-1,1],因此對時間變量t作變換:

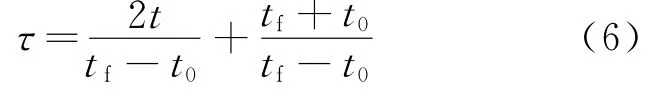
在本文研究問題中可取t0=0。

(2)插值多項式擬合

各種偽譜法主要區(qū)別之一是離散點的選擇不同。高斯偽譜法的離散點κ={τ1,τ2,…,τK}為K階Legendre-Gauss點,即K階Legendre多項式PK(τ)的根,其中

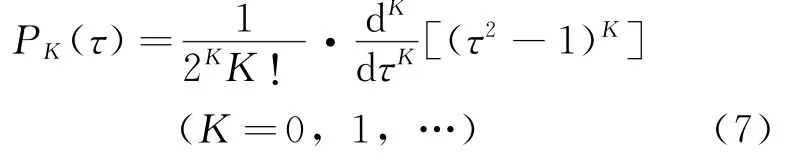
以[-1,1)上的K+1個插值點對應的Lagrange插值多項式Li(τ)(i=0,1,…,K)作為基函數(shù),近似狀態(tài)變量,即

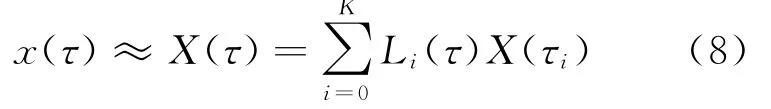
其中

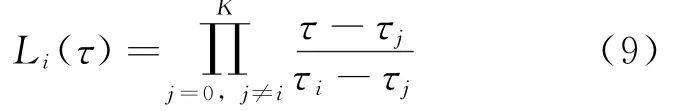
控制變量仍采用Lagrange插值多項式~Li(τ)(i=0,1,…,K)作為基函數(shù)來近似

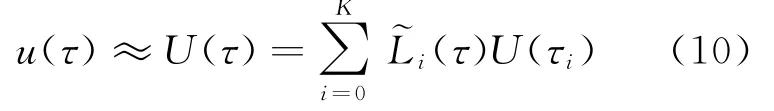
注意,這里控制變量u(τ)的Lagrange插值節(jié)點不一定與狀態(tài)變量x(τ)插值節(jié)點完全重合,相應地,它們的插值基函數(shù)也將不同。

(3)離散條件下的終端狀態(tài)約束

高斯偽譜法中的節(jié)點包括K個配點(τ1,τ2,…,τK)和初始點τ≡-1以及終點τ≡1。根據(jù)動力學方程有

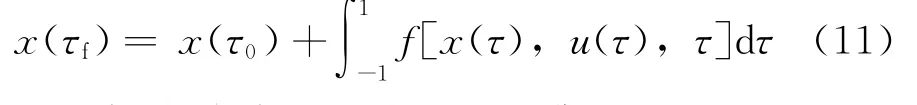
將終端狀態(tài)約束條件離散并用Gauss積分來近似,可得

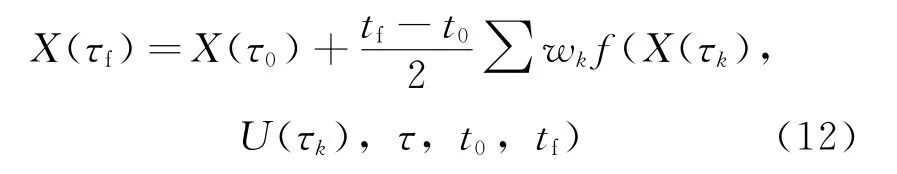
(4)微分方程約束轉換為代數(shù)約束

對式(8)求導有

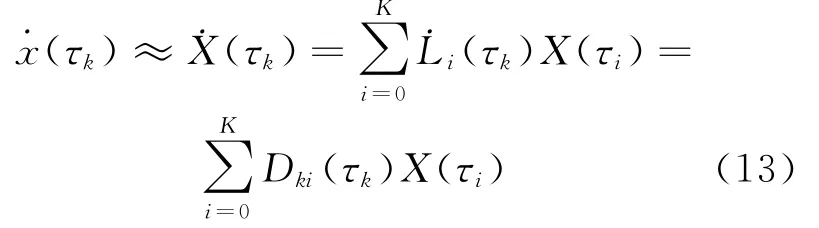
其中微分矩陣D∈RK×(K+1)可離線確定,其表達式為

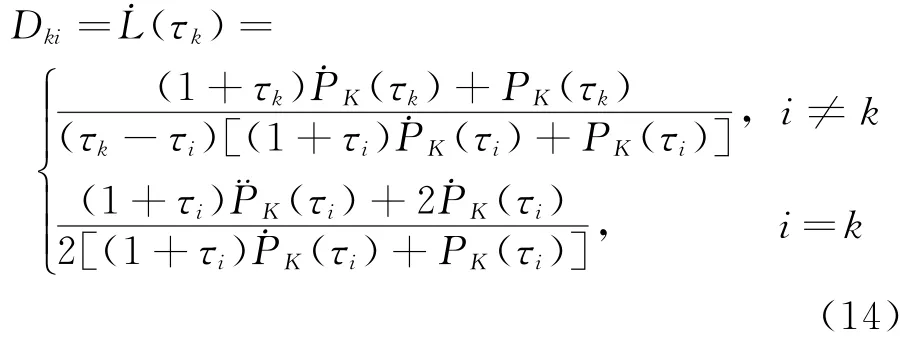
式中:τi(i=0,1,…,K)屬于集合κ0={τ0,τ1,…,τK}。將式(13)代入動力學方程˙X(τ)=f(X(τ),U(τ);t0,tf),得到狀態(tài)變量在配點上應滿足的代數(shù)方程

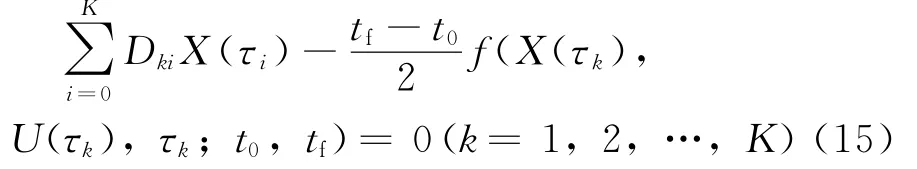
(5)離散化的近似性能指標函數(shù)

將Bolza型性能指標函數(shù)J=Φ(X0,t0,中的積分項用Gauss積分來近似,得到Gauss偽譜方法中的性能指標函數(shù)

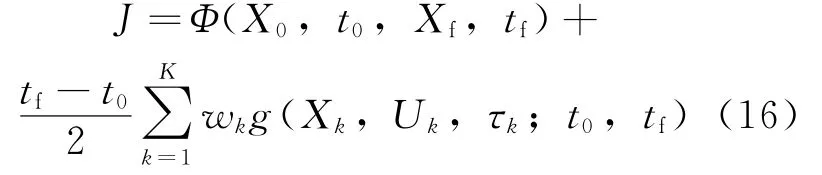
2.2 高斯偽譜法的一般描述

基于上述的數(shù)值近似方法,高斯偽譜法可將連續(xù)最優(yōu)控制問題離散化,并轉換為非線性規(guī)劃問題。離散最優(yōu)控制問題的一般描述為:求離散狀態(tài)變量Xi和控制變量Uk、初始時刻t0和終端時刻tf(如果t0和tf未知),使性能指標式(16)最小,并滿足配點處狀態(tài)約束式(15)以及終端狀態(tài)約束式(12),邊界條件為

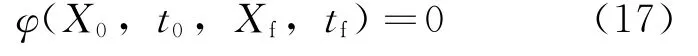
過程約束為

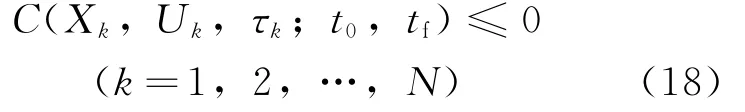
采用上述離散方法,連續(xù)最優(yōu)控制問題則轉化為非線性規(guī)劃問題。該非線性規(guī)劃問題統(tǒng)一描述為

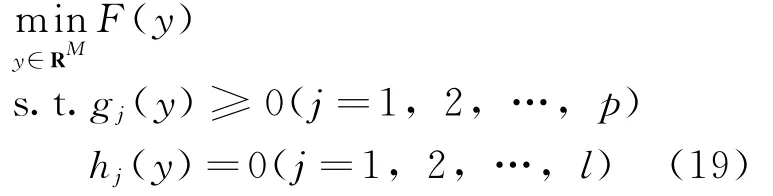
原連續(xù)時間動態(tài)系統(tǒng)和待優(yōu)化指標形成的最優(yōu)控制問題,經高斯偽譜法離散化轉化并進行全局多項式插值估計,最終可以轉化為對一個非線性規(guī)劃問題進行求解。該非線性規(guī)劃問題的KKT條件與最優(yōu)控制問題的一階必要條件離散形式是等價一致的。這就意味著在原理上該非線性規(guī)劃問題的解從數(shù)學原理上等價于原最優(yōu)控制問題的解。在非線性規(guī)劃問題求解過程中,通過KKT乘子可以對最優(yōu)控制問題的協(xié)變量進行非常準確的估計,再加上初始條件,就可以把最優(yōu)控制問題的一階必要條件相應的兩點邊值問題轉換為一個初值問題。從而一個動態(tài)優(yōu)化問題轉換為一系列的靜態(tài)優(yōu)化問題。

2.3 多階段轉移軌道的求解轉化

基于混合模式推進系統(tǒng)的同步衛(wèi)星轉移軌道被分為多個軌道段,在轉移軌道的每個階段內的衛(wèi)星狀態(tài)變量均光滑連續(xù),可以采用高斯偽譜法轉化成相應的NLP問題,各個階段之間順序關聯(lián),前一階段的tf與施加后一階段的t0相等,對前后兩個階段的時間統(tǒng)一處理為

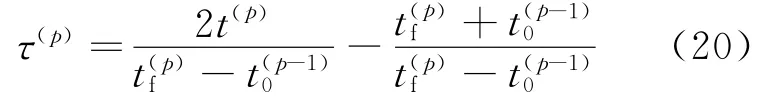
式中:上標表示階段數(shù),將兩個階段的時間[t(p-1)0,t(p)f]合并映射到[-1,1]。

狀態(tài)變量的關聯(lián)為

按照式(10)和式(11)對NLP問題中涉及的時間和狀態(tài)變量進行聯(lián)接,則將P個NLP問題構建成一個NLP問題。

3 算例仿真

為了驗證文中所研究方法的有效性,對基于混合模式推進系統(tǒng)的地球同步衛(wèi)星轉移軌道優(yōu)化過程進行仿真。仿真場景如下:星箭分離后,衛(wèi)星進入遠地點高度Ha0=35 786 km、近地點高度Hp0=200 km、軌道傾角i0=28.5°、升交點赤經Ω0=98°的初始軌道,此時衛(wèi)星的真近點角為θ0=179.30°,衛(wèi)星的初始質量為m0=5500 kg;衛(wèi)星所要到達的同步軌道的高度為35 786 km,軌道傾角if=0o,其他軌道參數(shù)沒有終端限制;化學發(fā)動機的推力為750 N,比沖為3120 m/s,電推力器單臺推力為150 m N,比沖為15000 m/s,電推變軌過程中,4臺推力器同時開機。以規(guī)定任務時限內燃料最省為優(yōu)化目標,求解地球同步軌道衛(wèi)星的最優(yōu)軌道轉移方案。這里所規(guī)定的任務時限即最長總變軌時間,將其作為優(yōu)化的時間約束條件。為簡化問題,仿真中忽略弧段、光照等因素的影響。

化學發(fā)動機的開機次數(shù)直接影響了轉移軌道的分段情況,進而影響問題求解的復雜程度,為說明高斯偽譜法在處理多階段最優(yōu)控制問題的有效性,現(xiàn)對不同任務時限下化學發(fā)動機在遠地點2次點火和4次點火的情況分別進行仿真分析。

3.1 化學發(fā)動機2次點火的情況

設定任務時限為70 d,通過對化學發(fā)動機開關機點的浮動限制將軌道轉移過程分為4段,依次為化推第1段、自由段、化推第2段、電推段,利用高斯偽譜法進行求解。

在配置為Intel Core i5-4440 CPU@ 3.10 GHz、RAM4.00 GB的64位計算機上在Matlab環(huán)境下進行求解,運算耗時43.1 h。算例求得的70天任務時限內滿足約束要求的最小燃料消耗質量是2 115.019 kg,軌道轉移時間為67.515 d。其中,化學發(fā)動機在遠地點進行2次開機變軌,化推段耗時11.772 h,消耗燃料1878.817 kg,單次最長開機時間為1.4534h,累計開機時間為2.1291 h;電推耗時67.024 d,消耗燃料236.202 kg。化推段與電推段交接點處的軌道參數(shù)為am=32 203.145 km,em=0.319,im=4.956°。

狀態(tài)量與控制量變化曲線如圖1所示,衛(wèi)星轉移軌道如圖2所示。從圖1、圖2中可以看出,狀態(tài)量變化以及求解得出的轉移軌道均較為平滑,能以較高精度滿足終端狀態(tài)要求,同時控制量的變化也處于約束范圍內,能很好地滿足變軌過程中的姿態(tài)控制要求。

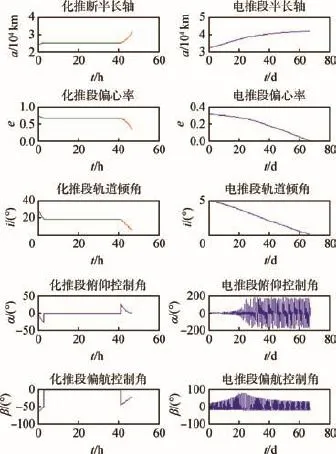
圖1 2次點火時狀態(tài)量與控制量變化曲線Fig.1 Change curve of state and control variables with two-time engine ignition

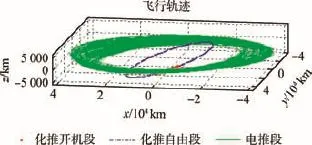
圖2 2次點火時衛(wèi)星轉移軌道Fig.2 Transfer orbit of satellite with two-time engine ignition

3.2 化學發(fā)動機4次點火的情況

化學發(fā)動機4次點火使轉移軌道更為復雜,為了減小數(shù)據(jù)運算量并保證得到收斂結果,這里將任務時限進行縮短,設定任務時限為30 d,通過對化學發(fā)動機開關機點的浮動限制將軌道轉移過程分為8段依次為化推第1段、自由段、化推第2段、自由段、化推第3段、自由段、化推第4段、電推段。

在相同的計算環(huán)境下,運算耗時9.3 h。算例求得的30 d任務時限內滿足約束要求的最小燃料消耗質量是2 308.686 kg,軌道轉移時間為30 d。優(yōu)化結果如表1所示,其中化學發(fā)動機在遠地點進行4次開機變軌,單次最長開機時間為0.680 h,累計開機時間為2.503 h,化推段與電推段交接點處的軌道參數(shù)為am=37 115.565 km,em=0.137,im=3.083°。

將相同條件下高斯偽譜法與遺傳算法的求解結果進行對比,如表1所示。可以看出高斯偽譜法得出的燃耗質量比遺傳算法少31.247 kg,兩種方法得出的變軌時間雖然都在30 d任務時限內,但遺傳算法優(yōu)化結果中衛(wèi)星歷經27.499 d就完成了軌道轉移任務,而高斯偽譜法得出的最優(yōu)解中,電推進的大比沖特性得到充分利用,用滿了整個任務時限,這樣會最大限度地壓縮化推變軌任務量,因而會減少整體燃料消耗質量。這些均說明了高斯偽譜法求解的最優(yōu)性、快速性、準確性。

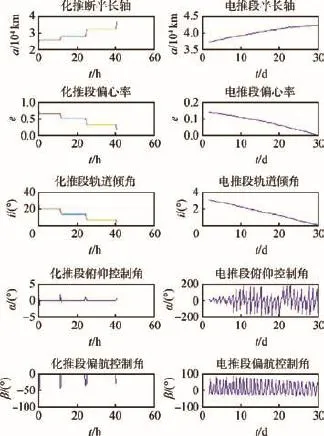
圖3 4次點火時狀態(tài)量與控制量變化曲線Fig.3 Change curve of state and control variables with four-time engine ignition

圖4 4次點火時衛(wèi)星轉移軌道Fig.4 Transfer orbit of satellite with four-time engine ignition

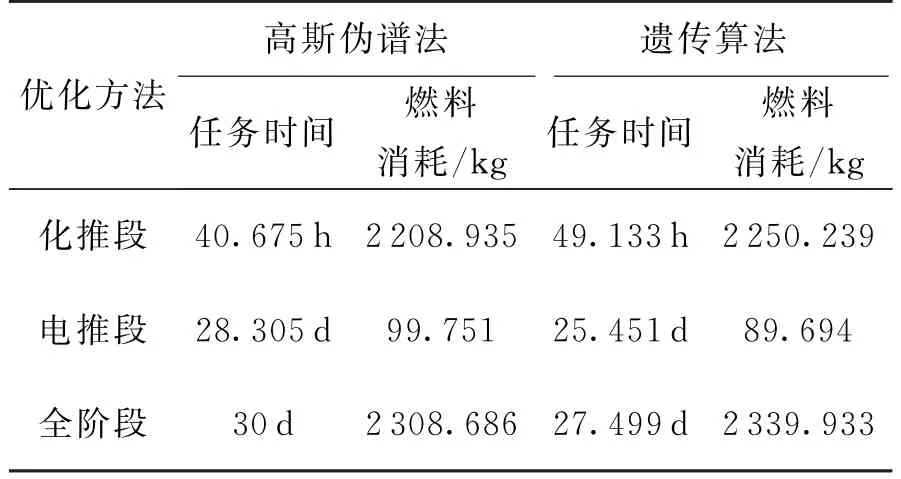
表1 化學發(fā)動機4次點火情況下不同優(yōu)化方法的軌道轉移結果對比Table 1 Comparison of orbit transfer results using different optimization methods under the circumstance of four-time engine ignition

4 結束語

本文針對地球同步軌道衛(wèi)星軌道轉移這一空間任務展開研究,分別從推進系統(tǒng)功能組成與軌道優(yōu)化算法兩方面對如何在任務允許時限內提高衛(wèi)星有效載荷進行了深入分析。提出一種綜合了化學發(fā)動機與電推力器性能優(yōu)勢的混合模式推進系統(tǒng),并基于此推進系統(tǒng)進行了多階段轉移軌道的優(yōu)化設計,提出了多階段轉移軌道的高斯偽譜法求解策略。通過求解分析與算例仿真得出如下結論:

1)混合模式推進系統(tǒng)綜合了化學發(fā)動機大推力、變軌時間短與電推力器高比沖、推進劑消耗低的優(yōu)勢,能夠在規(guī)定時限內以較高有效載荷完成軌道轉移任務,并且總體推進劑消耗質量小,入軌精度高。

2)本文提出的多階段轉移軌道的高斯偽譜法求解策略將分段點未知的分段最優(yōu)控制問題化成多個NLP問題,并通過分段點的關聯(lián)設置將多個NLP問題轉化為一個連貫的NLP問題。仿真結果表明,該方法能夠有效地對不同階段數(shù)、不同約束情況下的轉移軌道優(yōu)化問題進行求解,魯棒性強,收斂性好,對段間猜測值不敏感,且具有一定的通用性。

3)高斯偽譜法具有優(yōu)越的計算性能,運算效率高,能夠保證求解的最優(yōu)性,而遺傳算法的求解帶有一定的隨機性,其求解最優(yōu)性建立在大量的種群數(shù)量與遺傳次數(shù)之上,這無疑加大了運算量,因此高斯偽譜法具備較高的工程應用價值。

References)

[1] 湯國建,張洪波.小推力軌道機動動力學與控制[M].北京:科學出版社,2013.

[2] 袁建平,和興鎖.航天器軌道機動動力學[M].北京:宇航出版社,2010.

[3] 王小軍,吳德隆,余夢倫.地球同步衛(wèi)星遠地點最省燃料小推力多次變軌[J].中國空間科學技術,1995,15(4): 1-9. WANG X J,WU D L,YU M L.Mnimum-fuel lowthrust multiple-burn apogee maneuver for the geostationarysatellite[J].Chinese Space Science and Technology, 1995,15(4):1-9(in Chinese).

[4] KLUEVER C A.Optimal geostationary orbit transfers using onboard chemical-electric propulsion[J].Journal of Spacecraft and Rockets,2012,49(6):1174-1182.

[5] 吳受章.最優(yōu)控制理論與應用[M].北京:機械工業(yè)出版社,2008.

[6] 任遠,崔平遠,欒恩杰.基于退火遺傳算法的小推力軌道優(yōu)化問題研究[J].宇航學報,2007,28(162-166). REN Y,CUI P Y,LUAN E J.Low-thrust trajectory optimization based on annealing-genetic algorithm[J]. Journal of Astronautics,2007,28(162-166)(in Chinese).

[7] BETTS J T.Very low-thrust trajectory optimization using a direct SQP method[J].Journal of Computational and Applied Mathematics,2000,120(1-2):27-40.

[8] BETTS J T.Optimal interplanetary orbit transfers by direct transcription[J].Journal of the Astronautical Sciences,1994,42:247-268.

[9] 楊博,唐文國.基于電火箭推進的地-月軌道轉移自主導航研究[J].航天控制,2009,27(1):25-30. YANG B,TANG W G.Autonomous navigation for earthmoon orbital transfer based on electric propulsion[J]. Aerospace Control,2009,27(1):25-30(in Chinese).

[10] 尚海濱,崔平遠,徐瑞,等.基于高斯偽光譜的星際小推力轉移軌道快速優(yōu)化[J].宇航學報,2010,31(4): 1005-1011. SHANG H B,CUI P Y,XUN R,et al.Fast optimization of interplanetary low-thrust transfer trajectory based on gauss pseudospectral algorithm[J]. Journal of Astronautics,2010,31(4):1005-1011(in Chinese).

[11] 涂良輝,袁建平,羅建軍.基于偽光譜方法的有限推力軌道轉移優(yōu)化設計[J].宇航學報,2008,29(4): 1189-1193. TU L H,YUAN J P,LUO J J.Optimal design of orbital transfer with finite thrust based on Legendre pseudospectral method[J].Journal of Astronautics, 2008,29(4):1189-1193(in Chinese).

[12] 嚴輝,吳宏鑫,吳新珍.小推力軌道優(yōu)化研究[J].中國空間科學技術,1998,18(2):8-13. YAN H,WU H X,WU X Z.Study on optimization of low-thrust trajectories[J].Chinese Space Science and Technology,1988,18(2):8-13 (in Chinese).

[13] 王劼,崔乃剛,劉暾.小推力登月飛行器軌道初步研究[J].飛行力學,2000,18(2):46-49. WANG J,CUI N G,LIU D.Preliminary study on minimum-fuel lunar probe trajectories[J].Flight Dynamics,2000,18(2):46-49(in Chinese).

[14] KECHICHIAN J A.Optimal low-thrust rendezvous using equinoctial orbit elements[J].Acta Astronautica,1996, 38(1):1-14.

[15] ZONDERVAN K P,WOOD L J,CAUGHEY T K. Optimal low-thrust three-burn orbit transfer with large plane changes[J].Journal of the Astronautical Sciences,1984,32(3):407-427.

(編輯:高珍)

Optimal design of orbital transfer with chemical-electric hybrid propulsion system based on a new Gauss pseudospectral method

YANG Bo1,*,CHEN Ziyun1,WEN Zheng2,MIAO Jun1
1.School of Astronautics,Beihang University,Beijing 100191,China 2.Institute of Telecommunication Satellite,China Academy of Space Technology,Beijing 100094,China

A kind of chemical-electric hybrid mode propulsion system was proposed for the orbit transfer mission of GEO satellite.This propulsion system has a good application prospect and can fit much of the engineering demands,such as high-degree payloads and high-accuracy orbit insertion.The research on the optimization methods of the transfer orbit based on the hybrid mode propulsion system was carried out.A new Gauss pseudospectral method to solve the multi-phase optimum control problem was proposed,which transformed the multiple nonlinear programming problems transformed by Gauss pseudospectral method to one by setting up the linkage of the breaking points.Two simulation examples indicate thatthis method can effectively solve the optimization problem of the multi-phase non-smooth orbit.It has the advantages of high operation efficiency,big convergence radius and high solving accuracy,and can conveniently and fast process the optimization design of the transfer orbit based on the hybrid mode propulsion system.

electric propulsion;hybrid mode;multi-phase;geosynchronous orbit;Gauss pseudospectral method

V412.21

:A

10.3780/j.issn.1000-758X.2016.0006

2015-11-12;

:2015-12-08;錄用日期:2016-01-18;< class="emphasis_bold">網(wǎng)絡出版時間

時間:2016-02-24 13:42:02

http:∥www.cnki.net/kcms/detail/11.1859.V.20160224.1342.014.html

國家重點項目基金(91016004)

陳子勻(1988-),男,碩士研究生,chenziyun@163.com

*通訊作者:楊博(1963-),女,副教授,研究方向為飛行器自主導航技術、深空探測自主導航與制導技術、可重復運載器GNC關鍵技術引用格式:楊博,陳子勻,溫正,等.基于高斯偽譜法的化-電混合推進系統(tǒng)轉移軌道優(yōu)化設計[J].中國空間科學技術,2016,36(1):18-25.YANG B,CHEN Z Y,WEN Z,et al.Optimal design of orbital transfer with chemical-electric hybrid propulsion system based on a new Gauss pseudospectral method[J].Chinese Space Science and Technology,2016,36(1):18-25(in Chinese).

http:∥zgkj.cast.cn