一類新的（k＋2，k）Hadamard MSR碼

張司娜， 唐小虎， 李 杰

（西南交通大學信息科學與技術學院，四川成都610031）

一類新的（k＋2，k）Hadamard MSR碼

張司娜， 唐小虎， 李 杰

（西南交通大學信息科學與技術學院，四川成都610031）

為降低分布式存儲系統中節點的存儲量，構造了一類新（k＋2，k）Hadamard MSR碼．該碼的每個編碼矩陣皆對應于2個值，供其對角元素選取．在編碼矩陣中，這2個值循環出現，且不同的矩陣，循環出現的周期不同．基于這一特性構造了節點的修復方案，將失效節點中的α個數據分成α／2組，每一組重建2個數據，其他k＋1個節點為每一組各提供1個數據．證明了若新碼編碼矩陣的對角元素可取的2個值不相等，則可最優修復系統節點；若所有編碼矩陣對角元素可取的2個值的和為同一不為0的值，則可最優修復第1個校驗節點；若所有編碼矩陣對角元素可取的2個值的逆的和為1，則可最優修復第2個校驗節點．新碼的節點存儲量降低到了Hadamard MSR碼的理論界，可最優修復任意系統節點和1個校驗節點．

分布式；存儲；再生碼；MSR碼；高碼率；最優；修復

分布式存儲系統利用大量節點提供海量數據的存儲服務，具有成本低、易擴展等優點，在云計算、云存儲等有著廣泛的應用，如OceanStore［1］、Total Recall［2］、DHash＋＋［3］．

為了保證數據的可靠性和可用性，分布式存儲系統必須保持一定的數據冗余．糾刪碼就是一種重要的冗余存儲機制，其磁盤利用率高．現有采用糾刪碼方案的分布式存儲系統有Facebook的Hadoop、Google Colossus與Microsoft Azure［4］．

基于糾刪碼，將一個大小為M＝kα的文件編碼成同樣大小的n份（大小為α），任意k份都可恢復出原文件，即具有MDS（maximum distance separable）性質．在糾刪碼中，節點中的數據被視為標量，所以，當一個節點失效，為修復其數據（大小為α），需要從其他k個節點下載其全部數據，換言之，為修復M／k個數據，糾刪碼需要下載M個數據．

近年來，文獻［5］提出了最小存儲再生（minimum storage regenerating，MSR）碼，該碼具有MDS性質，磁盤利用率與糾刪碼相同．該碼將節點中的數據視為矢量，在修復失效節點的M／k個數據時，從其他d個（d≥k）可用節點下載其部分數據［6］，下載的數據總量（稱為修復帶寬）為dM／k（d－k＋1）＜M．

（n＝k＋2，k）系統MSR碼具有以下優勢：

（1）重建原文件時，若選取系統節點，無需計算；

（2）與其他MSR碼相比，存儲開銷最小［7-8］．

現有的（n＝k＋2，k）系統MSR碼見文獻［9-15］．其中，文獻［9］提出的Hadamard MSR碼的系統節點與校驗節點中的同一層數據恰好組成一個標量MDS碼．這一特性不僅使得Hadamard MSR碼可直接用于基于糾刪碼的分布式存儲系統，而且當某一系統節點中的數據變更時，所有校驗節點只需變更同層的數據，即具有最優更新性質．

文獻［16］證明了（k＋2，k）Hadamard MSR碼的節點存儲量α的下界為2k，然而，文獻［9］提出的Hadamard MSR碼的節點存儲量α＝2k＋1，是下界的2倍．

本文構造了一個新的（k＋2，k）Hadamard MSR碼．新碼的節點存儲量α達到了理論界2k，具有最優更新性質，可最優修復所有系統節點，雖然只能最優修復一個校驗節點，但對整個系統性能的影響較小，系統節點數遠大于2，其失效概率遠大于校驗節點，而且與校驗節點相比，系統節點的失效更嚴重，因為后者導致原始數據的丟失，增大用戶訪問信息的時恒．

1 （k＋2，k）Hadamard MSR碼的結構與修復特性

在域Fq上，用（k＋2，k）系統MSR碼對一個大小為M＝kα的文件進行編碼，生成k＋2份大小均為α的數據．其中，k份包含的是原始數據，另2份是原始數據的線性表達．這k＋2份數據分別存儲于k＋2個存儲節點．存儲原始數據的節點稱為系統節點，其他存儲節點稱為校驗節點．若將節點i（1≤i≤k＋2）中的數據用一個α維列向量ci表示，

不失一般性，校驗節點k＋1中的數據可表示為所有系統節點中的數據之和，即

校驗節點k＋2中的數據可表示為所有系統節點中數據的線性組合，即

其中，Ai（1≤i≤k）是α×α的矩陣，稱為系統節點i的編碼矩陣．若該系統MSR碼選用（k＋2，k）Hadamard MSR碼，編碼矩陣A1，A2，…，Ak均為對角矩陣，其編碼矩陣Ai（1≤i≤k）可表示為

其中，ai，l∈Fq，1≤l≤α．（k＋2，k）Hadamard MSR碼的結構如表1所示．

由表1可以看出，在（k＋2，k）Hadamard MSR碼中，校驗節點中的數據僅與系統節點中同層的數據相關，而與其他層的數據無關．因而，在某一系統節點中的數據變更時，所有校驗節點只需變更同層的數據，換言之，（k＋2，k）Hadamard MSR碼具有最優更新性質．由表1還可以看出，在每一層，（c1，l，…，ck，l，ck＋1，l，ck＋2，l）均是一個（k＋2，k）標量MDS碼，1≤l≤α，所以，（k＋2，k）Hadamard MSR碼可看作α層標量MDS碼的組合．顯然，若（k＋2，k）Hadamard MSR碼具有MDS性質，需要編碼矩陣的對角元素滿足ai，l≠0與ai，l－aj，l≠0，其中，1≤i≠j≤k，1≤l≤α．

表1 （k＋2，k）Hadamard MSR碼的結構Tab．1 Structure of（k＋2，k）Hadamard MSR code

在（k＋2，k）Hadamard MSR碼中，失效節點的最優修復是分組進行、同層相助的［17］．在另外k＋1個節點的幫助下，失效節點中數據（大小為α）的修復是分成α／2組并行進行的，每一組負責重建2個數據，若失效節點的第l層與第s層（l≠s）的數據分為一組進行修復，為重建這2個數據，每一個幫助節點提供的數據（大小為1）也是由各自的第l層與第s層數據生成的．

2 一類新的（k＋2，k）Hadamard MSR碼

文獻［9］提出的（k＋2，k）Hadamard MSR碼的節點存儲量α為2k＋1，是文獻［16］給出的理論界的2倍．為降低節點存儲量，本文對其進行了改進，構造了一類新的（k＋2，k）Hadamard MSR碼．新碼的節點存儲量α為2k，降低到了理論界．

（k＋2，k）MSR碼由編碼矩陣A1，A2，…，Ak組成，而（k＋2，k）Hadamard MSR碼的編碼矩陣均為對角陣．

在新（k＋2，k）Hadamard MSR碼中，編碼矩陣Ai（1≤i≤k）主對角線上的元素ai，l（1≤l≤α＝2k＋1）取值為

即，編碼矩陣

為方便后續定理的證明，將新碼編碼矩陣對角元素的取值規律以引理的形式表示．

引理1 ai，l＝ai，l＋2i－1，aj，l與aj，l＋2i－1一個取μi，另一個取νi，其中，1≤i≠j≤k，l∈［2is＋1，2is＋2i－1］，0≤s≤2k－i－1．

證明 根據式（1），引理1等價于

當i＜j時，不失一般性，令

則有

而

則有

引理2 ai，l與ai，2k－l＋1一個取μi，另一個取νi，其中，1≤i≤k，l∈［1，2k－1］．證明 不失一般性，令

則

根據式（1），ai，l與ai，2k－l＋1一個取μi，另一個取νi．

2．1 系統節點的最優修復方案

在新（k＋2，k）Hadamard MSR碼中，系統節點i（1≤i≤k）的修復是將第l層（l∈［2is＋1，2is＋2i－1］，0≤s≤2k－i－1）與第l＋2i－1層分為一組，為修復該組數據，其他系統節點與校驗節點提供的數據均是這2層的數據之和．

下面證明編碼矩陣的對角元素的取值μi與νi（1≤i≤k）滿足何種條件時，新（k＋2，k）Hadamard MSR碼可最優修復系統節點．

定理1 若μi≠νi（1≤i≤k），新（k＋2，k）Hadamard MSR碼可最優修復所有系統節點．

證明 系統節點i（1≤i≤k）中的數據為ci，1，ci，21，…，ci，2k，為重建ci，l與ci，l＋2i－1（l∈［2is＋1，2is＋2i－1］，0≤s≤2k－i－1），從其他系統節點下載

從校驗節點k＋1下載ck＋1，l＋ck＋1，l＋2i－1，即為

從校驗節點k＋2下載ck＋2，l＋ck＋2，l＋2i－1，即為

由引理1可知，aj，l＝aj，l＋2i－1，因而，式（3）與式（4）的最后一項都可由式（2）消去，而式（3）的第1項與式（4）的第1項組成關于ci，l與ci，l＋2i－1的方程組，只要ai，l≠aj，l＋2i－1，該方程組可解．

由引理1知，ai，l與aj，l＋2i－1一個取μi，另一個取νi，所以，只要μi≠νi，則可解出ci，l與ci，l＋2i－1．

因此，若μi≠νi（1≤i≤k），新（k＋2，k）Hadamard MSR碼可最優修復所有系統節點．

2．2 校驗節點的最優修復

新（k＋2，k）Hadamard MSR碼無法保證2個校驗節點均可最優修復，只能選取一個進行最優修復．

若可最優修復校驗節點k＋1，其修復是將第l層（l∈［1，2k－1］）與第2k－l＋1層分為一組．為修復該組數據，系統節點提供的數據是這2層數據之和，而校驗節點k＋2提供的則是這2層數據之差．

下面證明編碼矩陣對角元素的取值μi與νi（1≤i≤k）滿足何種條件時，新（k＋2，k）Hadamard MSR碼可最優修復校驗節點k＋1．

定理2 若μ1＋ν1＝μ2＋ν2＝…＝μk＋νk≠0，新（k＋2，k）Hadamard MSR碼可最優修復校驗節點k＋1．

證明 校驗節點k＋1中的數據為ck＋1，1，ck＋1，21，…，ck＋1，2k，為重建ck＋1，l與ck＋1，2k－l＋1（l∈［1， 2k－1］），從k個系統節點下載

將式（5）的所有項相加，得

從校驗節點k＋2下載ck＋2，l－ck＋2，2k－l＋1，即為

式（6）與式（7）組成關于ck＋1，l與ck＋1，2l－l＋1的方程組，若要方程組可解，需要a1，l＋a1，2k－l＋1≠0并且式（7）的最后一項可消去，即

由引理2可知，ai，l與ai，2k－l＋1一個取μi，另一個取νi，即

那么，只要

則可解出ck＋1，l與ck＋1，2l－l＋1．

因此，若

新（k＋2，k）Hadamard MSR碼可最優修復校驗節點k＋1．

若新（k＋2，k）Hadamard MSR碼可最優修復校驗節點k＋2，其分組與修復校驗節點k＋1時相同，即第l層（l∈［1，2k－1］）與第2k－l＋1層分為一組．為修復該組數據，系統節點提供的數據是這2層的數據之和，而校驗節點k＋1提供的則是這2層的數據之差．

下面證明編碼矩陣的對角元素的取值μi與νi（1≤i≤k）滿足何種條件時，新（k＋2，k）Hadamard MSR碼可最優修復校驗節點k＋2．

定理3 若μ－1i＋ν－1i＝1（1≤i≤k），新（k＋2，k）Hadamard MSR碼可最優修復校驗節點k＋2．

證明 校驗節點k＋2中的數據為ck＋2，1，ck＋2，21，…，ck＋2，2k，為重建ck＋2，l與ck＋2，2k－l＋1（l∈［1，2k－1］），從k個系統節點下載

將式（8）的所有項相加，得

從校驗節點k＋1下載ck＋1，l－ck＋1，2k－l＋1，即為

式（9）與式（10）組成關于ck＋2，l與ck＋2，2k－l＋1的方程組，若要方程組可解，式（10）的最后一項需消去，即需

由引理2可知，ai，l與ai，2k－l＋1一個取μi，另一個取νi，即

那么，只要

則可解出ck＋2，l與ck＋2，2k－l＋1．

因此，若

新（k＋2，k）Hadamard MSR碼可最優修復校驗節點k＋2．

2．3 新碼的M DS性質

下面證明編碼矩陣的對角元素的取值μi與νi（1≤i≤k）滿足何種條件時，新（k＋2，k）Hadamard MSR碼滿足MDS性質．

定理4 若μi≠0，νi≠0，μi≠νi，μi≠μj，νi≠νj（1≤i≠j≤k），新（k＋2，k）Hadamard MSR碼具有MDS性質．

證明 若（k＋2，k）Hadamard MSR碼具有MDS性質，需要編碼矩陣的對角元素滿足ai，l≠0與ai，l－aj，l≠0（1≤i≠j≤k，1≤l≤α）．由式（1）知，新碼的ai，l取值μi或νi，則ai，l－aj，l的取值有4種，分別為μi－μj，νi－νj，μi－μj，νi－νj那么，若要ai，l≠0與ai，l－aj，l≠0同時成立，則需μi≠0，νi≠0，μi≠νj，μi≠μj，νi≠νj．

因此，若μi≠0，νi≠0，μi≠νj，μi≠μj，νi≠νj（1≤i≠j≤k），新（k＋2，k）Hadamard MSR碼具有MDS性質．

下面確定新（k＋2，k）Hadamard MSR碼需要多大的域．綜上所述，新碼若可最優修復所有系統節點且具有MDS性質，需要

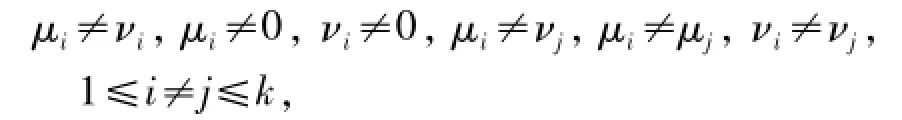
即要求μi，νi（1≤i≤k）為2k個不相同的非零數．而

（可最優修復校驗節點k＋1的充分條件）與

（可最優修復校驗節點k＋2的充分條件）均要求μi與νi（1≤i≤k）是k對和相同且和不為0的數．因此，新（k＋2，k）Hadamard MSR碼需要有限域Fq具有奇特征且q≥2k＋3．

在域Fq（q≥2k＋3）上，若新碼選擇最優修復校驗節點k＋1，μi與νi（1≤i≤k）可取

若選擇最優修復校驗節點k＋2，μi與νi（1≤i≤k）可取

其中，1≤t≤q－2．

3 結 論

本文給出了一類新的（k＋2，k）Hadamard MSR碼，其節點存儲量達到了Hadamard MSR碼的理論界．給出了節點的分組修復方案，基于該修復方案，證明了新碼可最優修復系統節點與校驗節點的充分條件．

［1］ RHEA S，WELLS C，EATON P，et al．Maintenancefree global data storage［J］．IEEE Internet Computing，2001，5（5）：40-49．

［2］ BHAGWAN R，TATI K，CHENG Y C，et al．Total recall：System support for automated availability management［C］∥Symposium Networked Systems Design and Imp lementation．San Francisco：ACM，2004：25-25．

［3］ DABEK F，LIJinyang，SIT E，etal．Designing a DHT for low latency and high throughput［C］∥Symposium Networked Systems Design and Implementation（NSDI）．San Francisco：ACM，2004：85-98

［4］ HUANG Cheng，SIMITCI H，XU Yi，et al．Erasure coding in windows azure storage［C］∥Usenix annual Technical Conference．Boston：ACM，2012：15-26．

［5］ DIMAKISA G，GODFREY P B，WU Yunnan，et al．Network coding for distributed storage systems［J］．IEEE Transactions on Information Theory，2010，56（9）：4539-4551．

［6］ 范文禮，劉志剛．基于傳輸效率矩陣的復雜網絡節點重要度排序方法［J］．西南交通大學學報，2014，49（2）：337-342．FAN Wenli，LIU Zhigang．Ranking method for node importance based on efficiency matrix［J］．Journal of Southwest Jiaotong University，2014，49（2）：337-342．

［7］ DIMAKISA G，RAMCHANDRAN K，WU Yunnan，et al．A survey on network codes for distributed storage［J］．Proceedings of the IEEE，2011，99（3）：476-489．［8］ 郝杰，逯彥博，劉鑫吉，等．分布式存儲中的再生碼綜述［J］．重慶郵電大學學報：自然科學版，2013，25（1）：30-38．HAO Jie，LU Yanbo，LIU Xinji，et al．Survey for regenerating codes for distributed storage［J］．Journal of Chongqing University of Posts and Telecommunications：Natural Science Edition，2013，25（1）：30-38．

［9］ PAPAILIOPOULOS D S，DIMAKIS A G，CADAMBE V R．Repair optimal erasure codes through hadamard designs［J］．IEEE Transactions on Information Theory，2013，59（5）：3021-3037．

［10］ TAMO I，WANG Zhiying，BRUCK J．Zigzag codes：MDS array codes with optimal rebuilding［J］．IEEE Transactions on Information Theory，2013，59（3）：1597-1616．

［11］ WANG Zhiying，TAMO I，BRUCK J．Long MDS codes for optimal repair bandwidth［C］∥Proceedings of IEEE International Symposium on Information Theory．Cambridge：IEEE，2012：1182-1186．

［12］ TAMO I，WANG Zhiying，BRUCK J．MDS array codes with optimal rebuilding［C］∥Proceedings of IEEE International Symposium on Information Theory．St．Petersburg：IEEE，2011：1240-1244．

［13］ CADAMBE V R，JAFAR S A，MALEKI H，et al．Asymptotic interference alignment for optimal repair of MDS codes in distributed storage［J］．IEEE Transactions on Information Theory，2013，59（5）：2974-2987．

［14］ CADAMBE V R，HUANG Cheng，LI Jin，et al．Polynomial length MDS codes with optimal repair in distributed storage［C］∥The 45th Asilomar Conference on Signals，Systems and Computers（ASILOMAR）．Pacific Grove：IEEE，2011：1850-1854．

［15］ CADAMBE V R，HUANG Cheng，LI Jin．Permutation code：Optimal exact-repair of a single failed node in MDS code based distributed storage systems［C］∥Proceedings of IEEE International Symposium on Information Theory Proceedings（ISIT）．St．Petersburg：IEEE，2011：1225-1229．

［16］ TAMO I，WANG Zhiying，BRUCK J．Access versus bandwidth in codes for storage［J］．IEEE Transactions on Information Theory，2014，60（4）：2028-2037．

［17］ TANG Xiaohu，YANG Bin，LI Jie．New repair strategy of hadamard minimum storage regenerating code for distributed storage system［J／OL］．（2013-12-18）［2014-12-10］．http：／／arxiv．org／pdf／1312．5173v1．pdf．

（中文編輯：唐 晴 英文編輯：周 堯）

A New（k＋2，k）Hadamard Minimum Storage Regenerating Code

ZHANG Sina， TANG Xiaohu， LI Jie
（School of Information Science and Technology，Southwest Jiaotong University，Chengdu 610031，China）

To reduce the storage capacity of nodes in distributed storage systems，a new（k＋2，k）Hadamard Minimum Storage Regenerating（MSR）code was constructed．Each coding matrix is related to two values，from which the diagonal elements of this coding matrix are selected．These two values appear in the coding matrix in a repeating pattern，but with different repeating cycles for different matrices．Based on the structure of the coding matrix，a repair strategy was constructed．The repair strategy divides symbols in the failed node intoα／2 groups with two symbols in each group，then the two symbols are recovered by downloading one symbol from each of the other k＋1 nodes．If the two values related to each coding matrix are unequal，the new Hadamard MSR code can optimally repair systematic nodes．If the sum of two values related to each coding matrix is nonzero and the k values are the same，the new Hadamard MSR code can optimally repair the first parity node．If the sum of the inverse of two values related to each coding matrix is one，the new Hadamard MSR code can optimally repair the second parity node．The new code reduces the storage capacity to the bond for Hadamard MSR code．Further，it can optimally repair all systematic nodes and one parity node．

distributed；storage；regenerating code；MSR code；high code-rate；optimal；repair

TN911．22

A

0258-2724（2016）01-0188-06 DO I：10．3969／j．issn．0258-2724．2016．01．026

2015-02-01

張司娜（1985—），女，博士研究生，研究方向為分布式存儲編碼，E-mail：nsz1221＠163．com

唐小虎（1971—），男，教授，博士生導師，研究方向為信息安全與編碼，E-mail：xhtang_scce＠home．swjtu．edu．cn

張司娜，唐小虎，李杰．一類新的（k＋2，k）Hadamard MSR碼［J］．西南交通大學學報，2016，51（1）：188-192，200．