基于高溫鑄坯黏彈塑性的坯殼動態鼓肚研究

韓培培　任廷志

燕山大學國家冷軋板帶裝備及工藝工程技術研究中心，秦皇島，066004

?

基于高溫鑄坯黏彈塑性的坯殼動態鼓肚研究

韓培培任廷志

燕山大學國家冷軋板帶裝備及工藝工程技術研究中心，秦皇島，066004

摘要：基于高溫鑄坯材料黏彈塑性本構方程，建立了坯殼動態鼓肚數學模型。根據坯殼不同的初始狀態與變形歷史確定了兩種邊界條件。利用模型計算坯殼鼓肚變形，并與實測數據進行對比，驗證了理論解的正確性以及模型的有效性。根據鞍鋼工業板坯連鑄機的設備工藝參數，分別計算了剛出結晶器的坯殼和遠離結晶器的坯殼的鼓肚變形曲線，以及坯殼在固液交界面處的應變與應變速率。分析了鑄坯坯殼在鑄機扇形段內的鼓肚變形與應變變化規律，并討論了輥間距、拉坯速度對坯殼鼓肚變形的影響。

關鍵詞：連鑄；鼓肚；黏彈塑性；應變

0引言

連鑄過程中鑄坯坯殼的變形情況將直接影響鑄坯的最終質量。由鋼水靜壓力造成的坯殼鼓肚變形是鑄坯內部裂紋產生的主要原因[1-2]。當鼓肚嚴重時，甚至導致鑄坯無法被拉出。另一方面，若在凝固前沿產生裂紋，富集溶質的鋼液會被吸入裂縫引起局部偏析。凝固末端支撐輥間坯殼鼓肚會造成富集溶質的鋼液向中心流動而形成中心偏析。這些內部缺陷會對產品性能產生影響，導致產品合格率降低。因此，準確計算鑄坯坯殼的鼓肚變形，對鑄機輥列的合理設計以及工藝參數的優化有著重要的意義。

很多研究者對鑄坯的鼓肚變形進行了研究。盛義平等[3]提出了兩端固支的黏彈性梁或板的坯殼鼓肚模型。王忠民等[4-5]提出了兩端固支兩端自由的黏彈性薄板計算模型以及四端固支的黏彈性矩形板計算模型。Kaijitani等[6]對鑄坯坯殼鼓肚進行了二維仿真，得到了非對稱的坯殼鼓肚變形曲線。Okamyra等[7]對鑄坯坯殼鼓肚進行了三維仿真，分別得到寬面與窄面的鼓肚，結果顯示當寬面與窄面的長度比值大于3時，窄面的影響可以忽略不計。上述這些文獻對坯殼鼓肚變形進行了理論與仿真研究，獲得了一些有價值的結論。

然而鑄坯在輥列間運行的過程中，坯殼并不是靜止在支撐輥上發生鼓肚變形。靜態模型的計算結果與實際鑄坯的鼓肚形態存在一定的差異。文獻[8-9]分別對鑄坯坯殼的鼓肚進行了測量，測量結果反映了坯殼動態黏彈塑性變形的一些特征，如測量的坯殼鼓肚量的最大點不在兩支撐輥之間鼓肚區間的中點，在支撐輥附近區域測量到坯殼的反向鼓肚。為此，本文基于高溫鑄坯材料的黏彈塑性本構方程對坯殼鼓肚進行動態分析，建立板坯坯殼鼓肚變形的動態數學模型。根據坯殼不同的初始狀態與變形歷史確定兩種邊界條件，利用模型計算坯殼鼓肚變形，并與實測數據進行對比。以工業連鑄機為例，利用該模型計算鑄坯坯殼的鼓肚變形，分析鑄機扇形段內坯殼鼓肚變形與應變變化規律，并討論鑄機設備工藝參數對鑄坯坯殼鼓肚變形的影響。

1連鑄板坯動態鼓肚數學模型

1.1高溫狀態下坯殼變形的本構方程

合適的本構方程是研究連鑄過程坯殼變形行為的前提。在連鑄過程中，坯殼處于高溫狀態，其變形過程中，應力有高度的應變速率敏感性，坯殼具有黏塑性特征[10-16]。文獻[8]對剛出結晶器的鑄坯進行了實驗研究，發現停止拉坯后，坯殼的鼓肚量隨時間顯著變化，停止拉坯20 s后，鑄坯坯殼同一測量點的鼓肚量增加一倍，從實驗角度驗證了坯殼鼓肚變形的黏塑性特點。考慮坯殼鼓肚變形中彈性變形也占有一定比重，利用麥克斯韋爾黏彈塑性模型將坯殼鼓肚總應變速率分為彈性應變速率與黏塑性應變速率兩部分，即

(1)

彈性部分滿足胡克定律：

(2)

對于高溫彈性模量，文獻[17-18]給出了其關于溫度的表達式。Pierer等[19]通過SSCC實驗[11]對不同的高溫彈性模量表達式進行評估，其中文獻[17]提出的高溫彈性模量表達式與實驗結果很好地吻合，其表達式為

E=3.146×104-22.56t+1.38×10-3t2

(3)

式中，t為材料溫度，℃。

對于黏塑性部分的本構關系，很多學者進行了相關研究[20-22]，其中描述材料黏塑性本構關系的Arrhenius定律認為，蠕變變形是一種熱激活過程；Norton定律則概括了冪函數形式的材料黏塑性本構方程。兩種定律的本構方程如下所示：

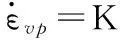
(4)

式中，Qa為激活能；Tk為絕對溫度；Ra為氣體常數，Ra=8.314J/(mol·K)；C′為與溫度有關的系數；n為應力指數；σ為應力。

這些本構方程在鑄坯坯殼變形的計算中得到了應用與驗證[23-24]。

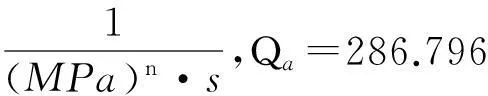
1.2坯殼鼓肚的動態受力模型

板坯的寬度通常是鑄坯輥間距2倍以上，因此兩輥之間的鑄坯坯殼的變形可以看作是承受均布載荷的兩端固支梁。在下側坯殼的中性軸建立直角坐標系Oxy，如圖1所示，假設整個區間所受壓力為p，坯殼的質量忽略不計。

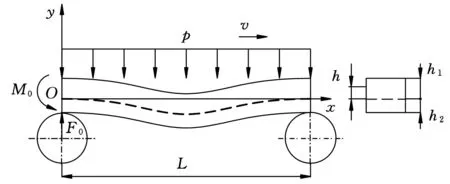
圖1　坯殼鼓肚的受力模型

通過求解下式得到坯殼中性軸的位置：

(5)

式中，σ為坯殼橫截面上任意一點的應力。

距中性軸距離h處的坯殼應變ε與坯殼變形曲線的曲率k(x)的關系為

ε=-k(x)h

(6)

位置為x處的坯殼所受彎矩M(x)與坯殼應力之間的關系為

M(x)=∫ShσdS

(7)

式中，h為坯殼橫截面上任意一點距中性軸的距離；S為坯殼橫截面的積分面積。

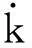
(8)

(9)

(10)

(11)

Iel=∫SEh2dS

(12)

Ivp=-∫S(-C′(-1/n)/n)exp(-Qa/RaTk)h1+1/ndS

由穩態澆鑄情況下的拉速v為定值可得

(13)

(14)

(15)

(16)

(17)

鑄坯坯殼變形曲線的方程y(x)與曲線曲率變化率的關系為

(18)

兩支撐輥間的鑄坯坯殼受力如圖1所示，鑄坯坯殼彎矩圖方程為

(19)

將式(18)與式(19)代入式(17)可得鑄坯坯殼變形曲線的動態黏彈塑性數學模型，鼓肚變形曲線的微分方程為

(20)

2板坯動鼓肚變形分析

對式(20)積分三次得到鑄坯坯殼鼓肚曲線方程y(x)，曲線方程y(x)有3個積分常數，加上M0、F0一共有5個未知數，需要5個方程才可求解。由鑄坯坯殼兩端的撓度為零，可得y(0)=y(L)=0。還需要三個邊界條件才可確定所有未知參數，因此需要進一步確定坯殼的邊界條件，根據鑄坯坯殼不同的初始狀態與變形歷史將邊界條件分為兩種。

第一種邊界條件不考慮坯殼變形歷史，如剛出結晶器的鑄坯，坯殼初始轉角為零。所施加的邊界條件為

(21)

式中， L為輥間距；θ(x)為鼓肚曲線的轉角。

第二種邊界條件考慮變形歷史。坯殼變形曲線在支撐輥兩端的曲率、轉角以及所受的彎矩相等，所施加的邊界條件為

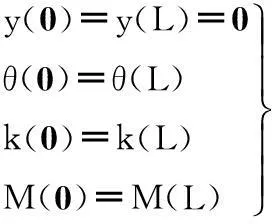
(22)

根據兩種邊界條件可以求得坯殼受力與變形曲線。由新日鐵[8]與住友金屬[9]的實驗鑄機確定相關參數，計算坯殼的鼓肚曲線，并將計算結果與實測結果進行對比。

2.1第一種邊界條件下的板坯鼓肚變形

新日鐵在小型垂直型實驗鑄機上，對剛出結晶器的鑄坯坯殼進行了測量[8]，測量輥列中第一輥與第二輥之間坯殼的鼓肚變形，位移傳感器固定在輥間位置為L/4、L/2、3L/4處，L=380mm。實驗中拉坯速度v=1.5m/min，測量位置的鋼水高度為1.4 m，坯殼厚度為20 mm。根據該實驗鑄機參數與工藝條件計算第一種邊界條件下坯殼鼓肚變形曲線，并將計算結果與測量結果[8]進行對比，如圖2所示。第一種邊界條件下的坯殼鼓肚變形曲線的特征如圖3所示。力能參數：Ivp=6.6740×1011(N·mm)n/s，Iel=2.7885×106N·mm。

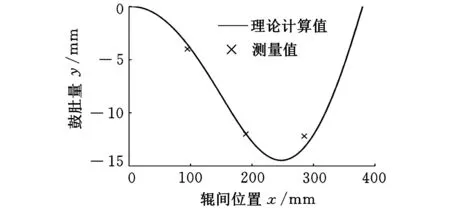
圖2　第一種邊界條件下坯殼鼓肚變形曲線與實驗測量值

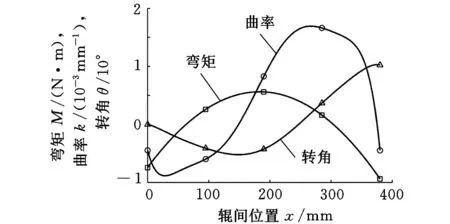
圖3　第一種邊界條件下坯殼鼓肚變形曲線特征

從圖2可以看出，在第一種邊界條件下坯殼的鼓肚變形計算結果與新日鐵對剛出結晶器的鑄坯坯殼測量結果較一致，最大鼓肚位于輥間中心位置下游。從圖3可以看出，鼓肚區間起點轉角為零，但在鼓肚區間末端，轉角不為零，并且在鼓肚區間兩端彎矩也不相等。顯然這種形式的鼓肚變形無法在輥列中實現連續。

2.2第二種邊界條件下的板坯鼓肚變形

住友金屬在弧形實驗鑄機上，用可移動的測量裝置對坯殼鼓肚進行了測量[9]。支撐輥處開有凹槽，位移傳感器可以對鼓肚區間的任意位置進行測量且測量長度大于輥間距。住友金屬的實驗鑄機半徑為3m，輥間距L=310mm，實驗中拉坯速度v=1.5m/min，測量位置的鋼水高度為2.8m，坯殼厚度為30mm。測得坯殼的長度為380mm。根據該實驗鑄機參數與工藝條件計算第二種邊界條件下的坯殼鼓肚變形曲線，并將計算結果與與測量結果[9]進行對比，如圖4所示。第二種邊界條件下的坯殼鼓肚變形曲線的特征如圖5所示。力能參數如下：Ivp=9.1342×1012(N·mm)n/s，Iel=8.5575×106N·mm。

從圖4可以看出，在該測量結果中，輥間位置0~70 mm區間，測量曲線與理論曲線存在一定偏差，但與理論曲線的趨勢是相同的。這可能是測量誤差造成的。輥間位置70~380 mm區間(1個輥間距長度)，測量曲線與理論曲線很好地吻合。輥間中心位置上游發生反向鼓肚，正向最大鼓肚位于輥間中心位置下游。從圖5可以看出，在第二種邊界條件下，鑄坯在鼓肚區間兩端的曲率、轉角、所受的彎矩均相等，這種鼓肚變形在輥列中可以實現連續。

3鼓肚變形計算實例與影響因素

根據鞍鋼工業板坯直弧形連鑄機的設備工藝參數計算輥列中不同位置鑄坯的鼓肚變形。該鑄機半徑R=9300 mm，板坯截面規格為230 mm×(900~1550)mm。鑄機輥列由18個扇形段構成，其中第1扇形段為彎曲段，第2~8扇形段為圓弧段，第9~10扇形段為矯直段，第11~18扇形段為水平段。鑄機常澆鋼種及主要成分如表1所示。

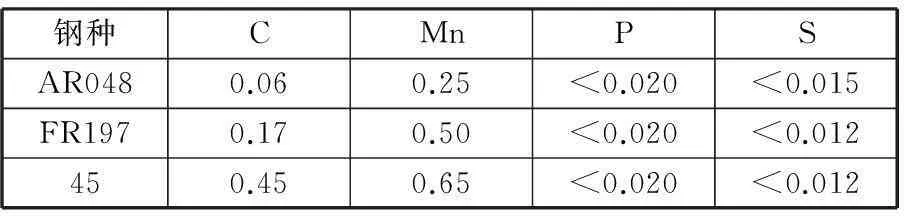
表1　常澆鋼種及主要成分(質量分數)　%

3.1剛出結晶器的鑄坯鼓肚變形

通過計算該鑄機第1扇形段的第一個輥間距內鑄坯坯殼的鼓肚，對剛出結晶器的鑄坯坯殼鼓肚變形規律進行分析。坯殼受力、固液交界面處的應變速率、應變、坯殼鼓肚曲線如圖6所示。輥間距為180 mm，拉坯速度為1.5 m/min，冶金長度區間為1.01~1.028 m，對應的鋼水高度為1.01~1.028 m，坯殼厚度根據冶金長度區間與拉坯速度確定。

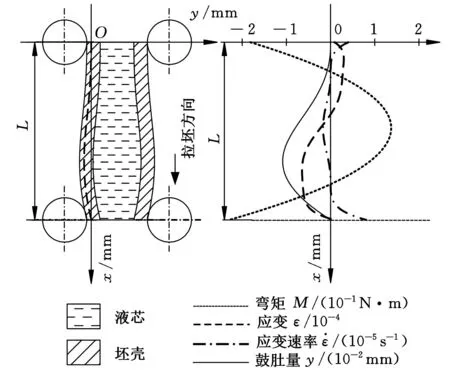
圖6　坯殼的鼓肚特征(剛出結晶器)

從圖6可以看出，剛出結晶器的坯殼均發生正向鼓肚，x=0處，坯殼所受彎矩為0.182 N·m，在x=L處，坯殼所受彎矩為0.229 N·m，固液交界面最大拉伸應變為0.3×10-4，最大應變速率為0.2×10-3s-1，最大鼓肚量為1.08×10-2mm。

3.2遠離結晶器的鑄坯鼓肚變形

通過計算鑄機第8扇形段坯殼的鼓肚，對遠離結晶器的鑄坯坯殼鼓肚變形規律進行分析。坯殼受力、固液交界面處的應變速率、應變、以及鑄坯坯殼鼓肚曲線如圖7所示。輥間距為357 mm，拉坯速度為1.5 m/min，第8扇形段的冶金長度區間為14.13~15.56 m，對應的鋼水高度為11.68~12.08 m，坯殼厚度根據冶金長度區間與拉坯速度確定。

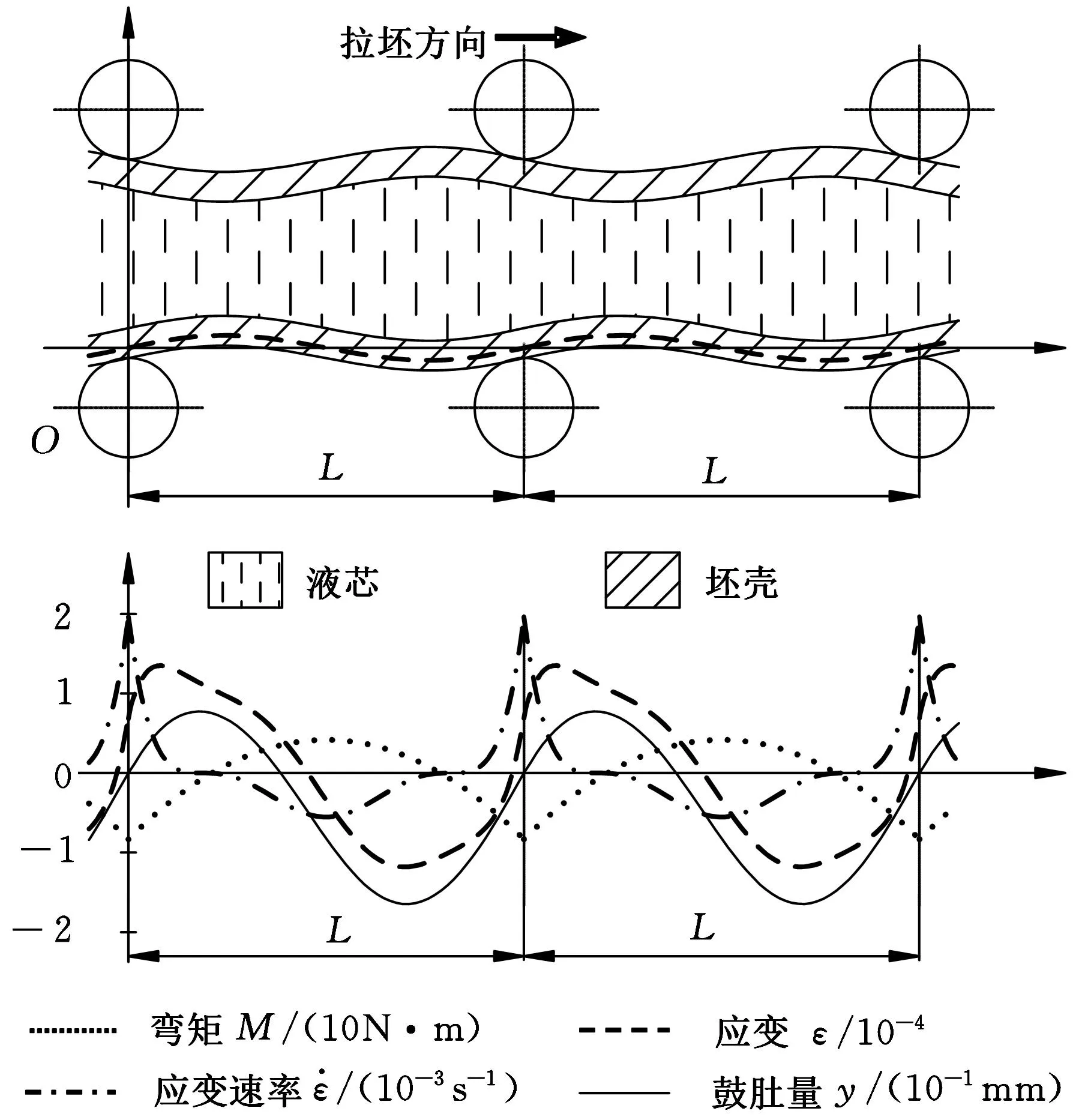
圖7　坯殼的鼓肚特征(第8扇形段)

從圖7可以看出，支撐輥下游存在反向鼓肚。x=0與x=L處，坯殼所受彎矩為8.7 N·m，固液交界面最大拉伸應變為1.3×10-4，最大應變速率為2×10-3s-1，最大正向鼓肚量為1.48×10-1mm，最大反向鼓肚量為0.87×10-1mm。

3.3鑄機設備工藝參數對鼓肚的影響

為了分析鑄機設備與工藝參數對坯殼鼓肚的影響，計算第8扇形段的鑄坯坯殼鼓肚，如圖8所示。拉坯速度為1.5 m/min。不同拉坯速度情況下，坯殼固液交界面最大應變與輥間距的關系如圖9所示。不同輥間距情況下，坯殼固液交界面的最大應變與拉坯速度的關系如圖10所示。

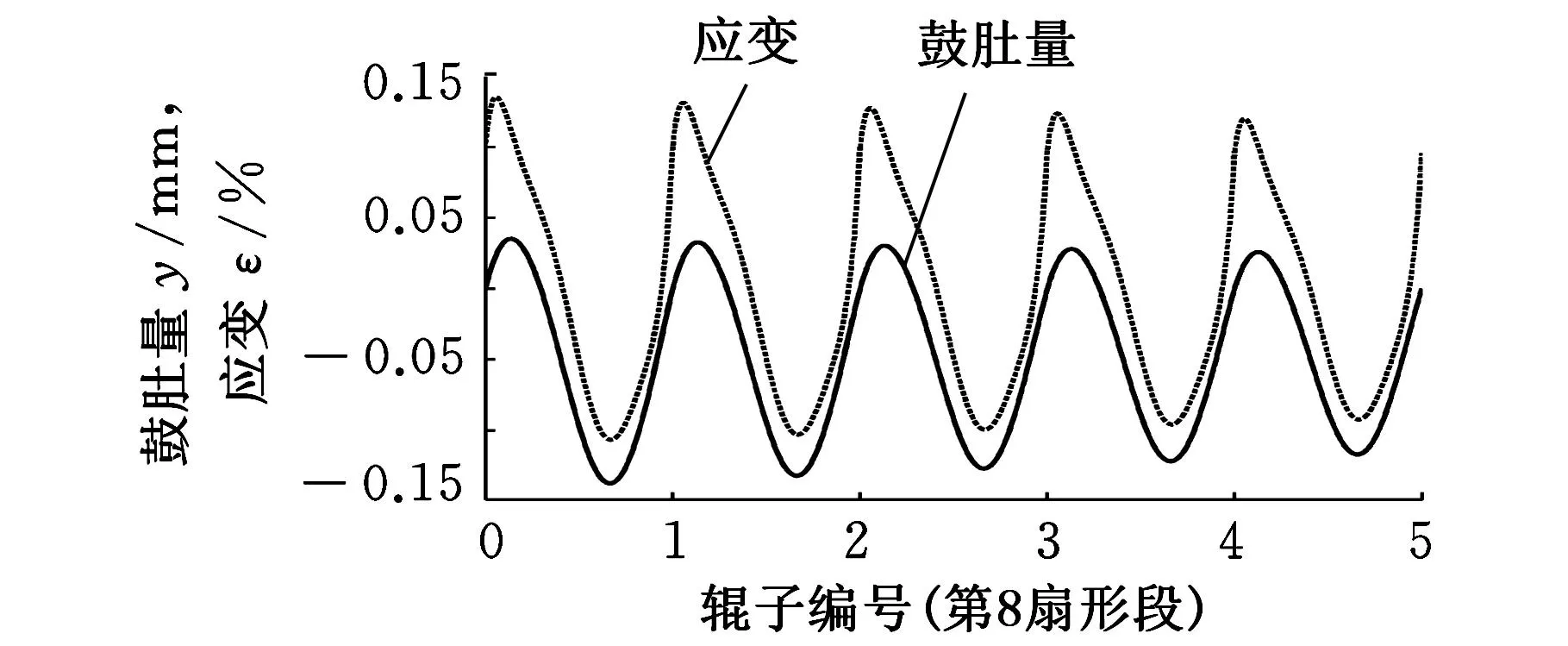
圖8　第8扇形段鑄坯坯殼的鼓肚特征

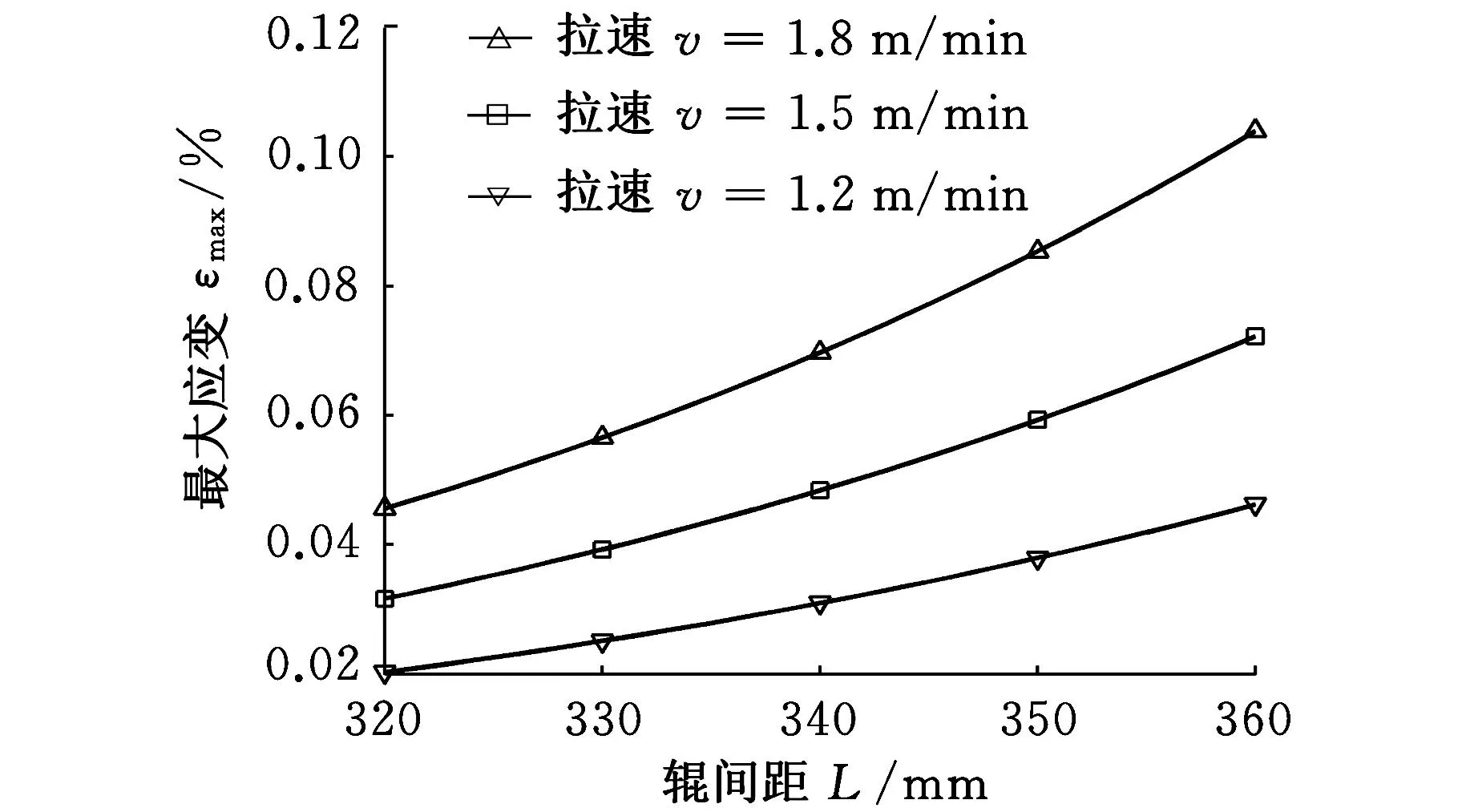
圖9　坯殼鼓肚最大應變與輥間距的關系

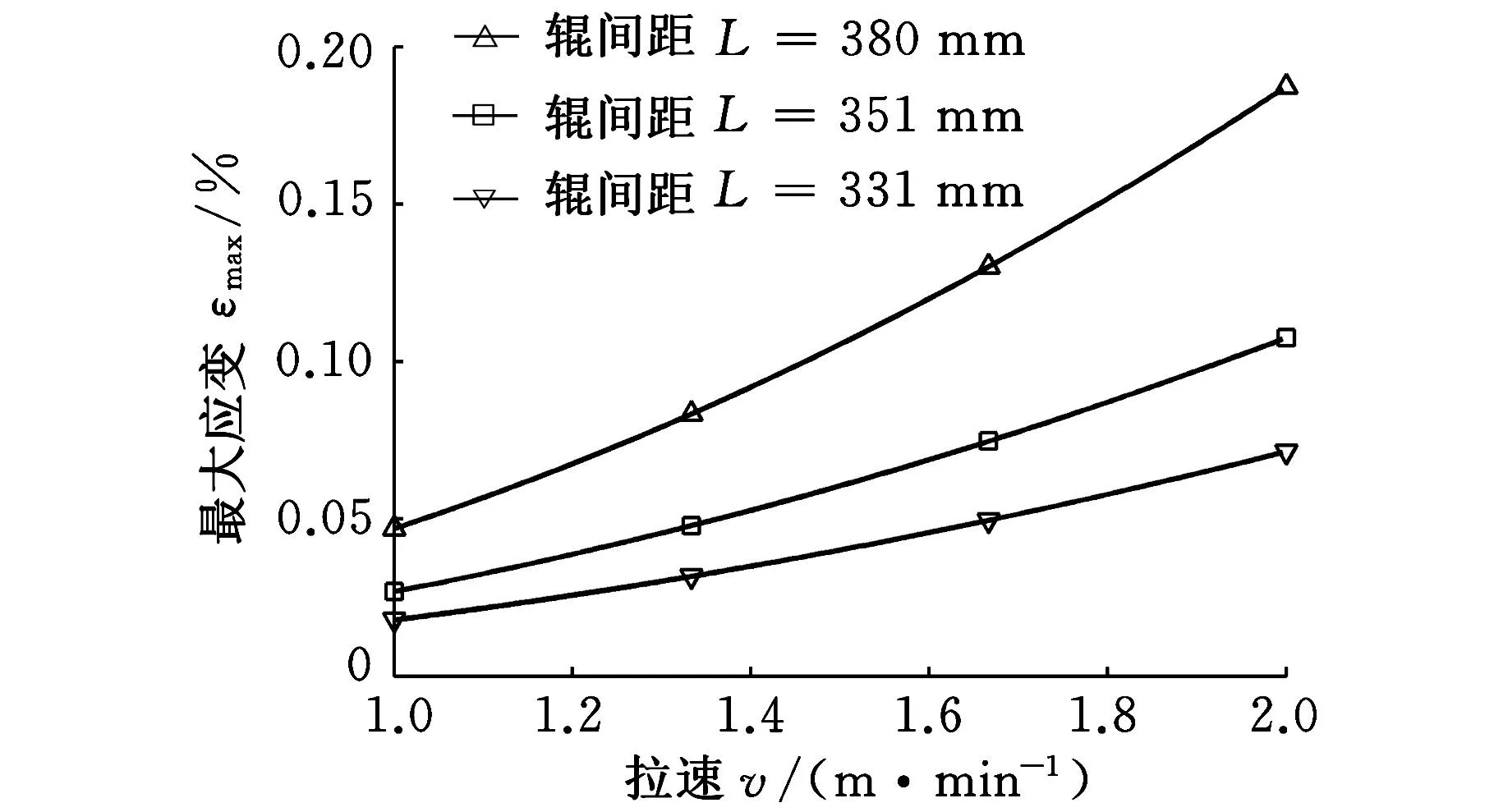
圖10　坯殼鼓肚最大應變與拉速的關系

從圖8可以看出，第8扇形段內，鑄坯坯殼的鼓肚量與坯殼固液交界面的應變逐漸減小，固液交界面的最大應變在1.5%以下，位于坯殼反向鼓肚區域。從圖9可以看出，拉速一定的情況下，固液交界面處的最大鼓肚應變隨著輥間距增加而增大。從圖10可以看出，輥間距一定的情況下，固液交界面處的最大鼓肚應變隨著拉坯速度的提高而增大。

4結論

(1)基于高溫材料黏彈塑性本構方程建立坯殼的動態鼓肚模型，模型的計算結果與實驗鑄機的測試結果吻合很好，證明了模型的有效性。

(2) 坯殼變形歷史以及初始狀態會對坯殼鼓肚變形產生影響。剛出結晶器的坯殼，發生第一種邊界條件下的鼓肚變形。隨著鑄坯在輥列中運行，鑄坯逐漸過渡到第二種邊界條件下坯殼的鼓肚變形。

(3)由于坯殼的黏彈塑性變形以及鑄坯的移動，坯殼的最大鼓肚從輥間中心位置向下游移動，支撐輥附近發生反向鼓肚，并且坯殼固液交界面最大拉伸應變位于坯殼反向鼓肚區域。鑄機設備與工藝參數制定要確保坯殼固液交界面的拉伸應變在安全范圍之內。

參考文獻：

[1]Verma R K, Girase N U. Comparison of Different Caster Designs Based on Bulging, Bending and Misalignment Strains in Solidifying Strand[J]. Ironmaking & Steelmaking, 2006, 33(6): 471-476.

[2]Li Chengbin, Thomas B G, Mei Feng. Prediction of Centerline Cracks Incurred in the Bloom Continuous Casting of Steel[J]. Baosteel Technical Research, 2010, 4(2): 40-43.

[3]盛義平, 孫薊泉, 章敏. 連鑄板坯鼓肚變形量的計算[J].鋼鐵, 1993, 28(3): 20-25.

Sheng Yiping, Sun Jiquan, Zhang Min. Calculation for Bulging Deformation of Continuously Casted Slab[J]. Iron and Steel, 1993, 28(3): 20-25.

[4]王忠民, 劉宏昭, 楊拉道,等. 連鑄板坯的黏彈性板模型及鼓肚變形分析[J]. 機械工程學報, 2001, 37(2): 66-69.

Wang Zhongmin, Liu Hongzhao, Yang Ladao, et al. Mathematical Model of Visco-elastic Thin Plate and Analyses of Bulging Deformation for Continuous Cast Slabs[J]. Chinese Journal of Mechanical Engineering, 2001, 37(2): 66-69.

[5]王忠民, 黃梓嫄. 基于辛幾何法分析連鑄板坯的黏彈性鼓肚變形[J]. 機械工程學報, 2014, 50(23): 82-88.

Wang Zhongmin, Huang Ziyuan. Viscoelastic Bulging Deformation Analysis of Continuous Casting Slab Based on the Symplectic Geometric Method[J]. Chinese Journal of Mechanical Engineering, 2014, 50(23): 82-88.

[6]Kajitani T, Drezet J M, Rappaz M. Numerical Simulation of Deformation-induced Segregation in Continuous Casting of Steel[J]. Metallurgical and Materials Transactions A, 2001, 32(6): 1479-1491.

[7]Okamyra K, Kawashima H. Three-dimensional Elasto-plastic and Creep Analysis of Bulging in Continuously Cast Slabs[J]. ISIJ International, 1989, 29(8): 666-672.

[8]Shigeyuki M, Kaname W, Yukio W. Analysis of Bulging in Continuously Cast Slabs[J]. Tetsu-to-Hagané, 1983, 69(12): S938.

[9]Sugitani Y, Masanori N. Measurement of Bulging in Continuous Casting Machine[J]. Tetsu-to-Hagane, 1984, 70(12): S898.

[10]Wang Wentao, Guo Xunzhong, Huan Bo. The Flow Behaviors of CLAM Steel at High Temperature[J]. Materials Science & Engineering A, 2014, 599: 134-140.

[11]Rowan M, Thomas B G, Bernhard C. Measuring Mechanical Behavior of Steel during Solidification: Modeling the SSCC Test[J]. Metallurgical and Materials Transaction B, 2011, 42(4): 837-851.

[12]Seid K,Thomas B G.Thermo-mechanical Models of Steel Solidification Based on Two Elastic Visco-plastic Constitutive Laws[J].Journal of Materials Processing Technology,2008,197(1/3):408-418.

[13]Huespe A E, Gardona A, Nigro N. Visco-plastic Constitutive Models of Steel at High Temperature[J]. Journal of Materials Processing Technology, 2000, 102(1/3): 143-152.

[14]Martin C L, Favier D, Suery M. Viscoplastic Behavior of Porous Metallic Materials Saturated with Liquid Part I: Constitutive Equations[J]. International Journal of Plasticity, 1997, 13(3): 215-235.

[15]Shigeyuki M, Kaname W, Yukio I. Analysis of Bulging in Continuously Cast Slabs[J]. Tetsu-to-Hagané, 1983,69(12): 226.

[16]Kozlowski P K, Thomas B G, Azzi J A. Simple Constitutive Equations for Steel at High Temperature[J]. Metallurgical Transaction A, 1992, 23(3): 903-918.

[17]Pühringer O M. Strand Mechanics for Continuous Slab Casting Plants[J]. Stahlund. Eisen.,1976,96(6):279-284.

[18]Kinoshita K, Emi T, Kasai M, Thermal Elasto-plastic Stress Analysis of Solidifying Shell in Continuous Casting Mold[J]. Tetsu-to-Hagané,1979,65(14):2022-2031.

[19]Pierer R, Bernhard C, Chimani C. Evaluation of Common Constitutive Equations for Solidifying Steel[J]. BHM Berg-und Hüttenm?nnische Monatshefte, 2005,150(5):163-169.

[20]Sakui S, Sakai T. Deformation Behavior of a 0.16% Carbon Steel in the Austenite Range[J]. Tetsu-to-Hagane, 1977, 63(2): 285-293.

[21]Beali E L. On the Mechanism of Halfway Cracks and Macro-segregation in Continuously Cast Steel Slabs (i). Halfway Cracks[J]. Scandinavian Journal of Metallurgy, 1995, 24(2): 63-80.

[22]Hetnarski R B, Eslami M R. Thermal Stress-advanced Theory and Applications[M]. Berlin: Springer, 2004.

[23]Hibbeler L C, Koric S, Xu K. Thermo-mechanical Modeling of Beam Blank Casting[J]. Iron and Steel Technology, 2009, 22(4): 8-14.

[24]Víctor D, Fachinotti, Alberto C. Constitutive Models of Steel under Continuous Casting Conditions[J]. Journal of Materials Processing Technology, 2003, 135: 30-43.

(編輯袁興玲)

Research on Dynamic Bulging of Continuous Casting Slab Based on

Elasto-viscoplastic Behavior of Metal at Elevated Temperature

Hai PeipeiRen Tingzhi

National Engineering Research Center for Equipment and Technology of Cold Strip Rolling,

Yanshan University,Qinhuangdao,Hebei,066004

Abstract:Based on elasto-viscoplastic behavior of metal at elevated temperature, a mathematical model of dynamic bulging with the movement of the slab between two rolls was developed. According to different initial conditions and the deformation history of a solidified shell, two groups of boundary conditions were presented. Then, in order to check the validity of this mathematical model, the calculated bulging profiles were compared with the measurements of bulging intensity and profiles on actual continuous casters. Then according to the casting parameters on different segments of an industrial caster in Ansteel company, the bulging of the solidified shell near mould and far from mould were exposed separately. In addition, the bulging features were analyzed including the bulging deflection, the bending moment acting on the solidified shell, the strain and the strain rate at the solid-liquid interface of the solidified shell. Finally, the bulging in a segment of the caster was calculated, and then the influences of the casting parameters including roll pitch and casting speed were analyzed.

Key words:continuous casting；bulging；elasto-viscoplastic；strain

基金項目：國家科技支撐計劃資助項目(2011BAF15B01)

收稿日期：2015-07-03

中圖分類號：TF777.1DOI：10.3969/j.issn.1004-132X.2015.23.004

作者簡介：韓培培，男，1986年生。燕山大學國家冷軋板帶裝備及工藝工程技術研究中心博士研究生。主要研究方向為高效連鑄裝備設計理論及工藝。任廷志(通信作者)，男，1960年生。燕山大學國家冷軋板帶裝備及工藝工程技術研究中心教授、博士研究生導師。